461. 汉明距离
题目来源:461. 汉明距离
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数 x 和 y,计算它们之间的汉明距离。
/** 方法一:直接计算异或后 1的个数 * @param {number} x * @param {number} y * @return {number} */ var hammingDistance = function(x, y) { return (x^y).toString(2).split(1).length-1; // return eval( (x^y).toString(2).split('').join('+') ); }; let x = 1, y = 16 console.log(x,y, hammingDistance(x,y)) /** 方法二:移位实现位计数 * @param {number} x * @param {number} y * @return {number} */ var hammingDistance = function(x, y) { let count = 0; let s = x^y; while(s!=0){ count +=s&1; s>>=1; } return count; }; x = 1, y = 16 console.log(x,y, hammingDistance(x,y)) /** 方法三:Brian Kernighan 算法 * @param {number} x * @param {number} y * @return {number} */ var hammingDistance = function(x, y) { let count = 0; let s = x^y; while(s!=0){ s &=s-1; count++; } return count; }; x = 1, y = 16 console.log(x,y, hammingDistance(x,y))
方法三:Brian Kernighan 算法
思路及算法
在方法二中,对于 s=(10001100)_2的情况,我们需要循环右移 8 次才能得到答案。而实际上如果我们可以跳过两个 1 之间的 0,直接对 1 进行计数,那么就只需要循环 3 次即可。
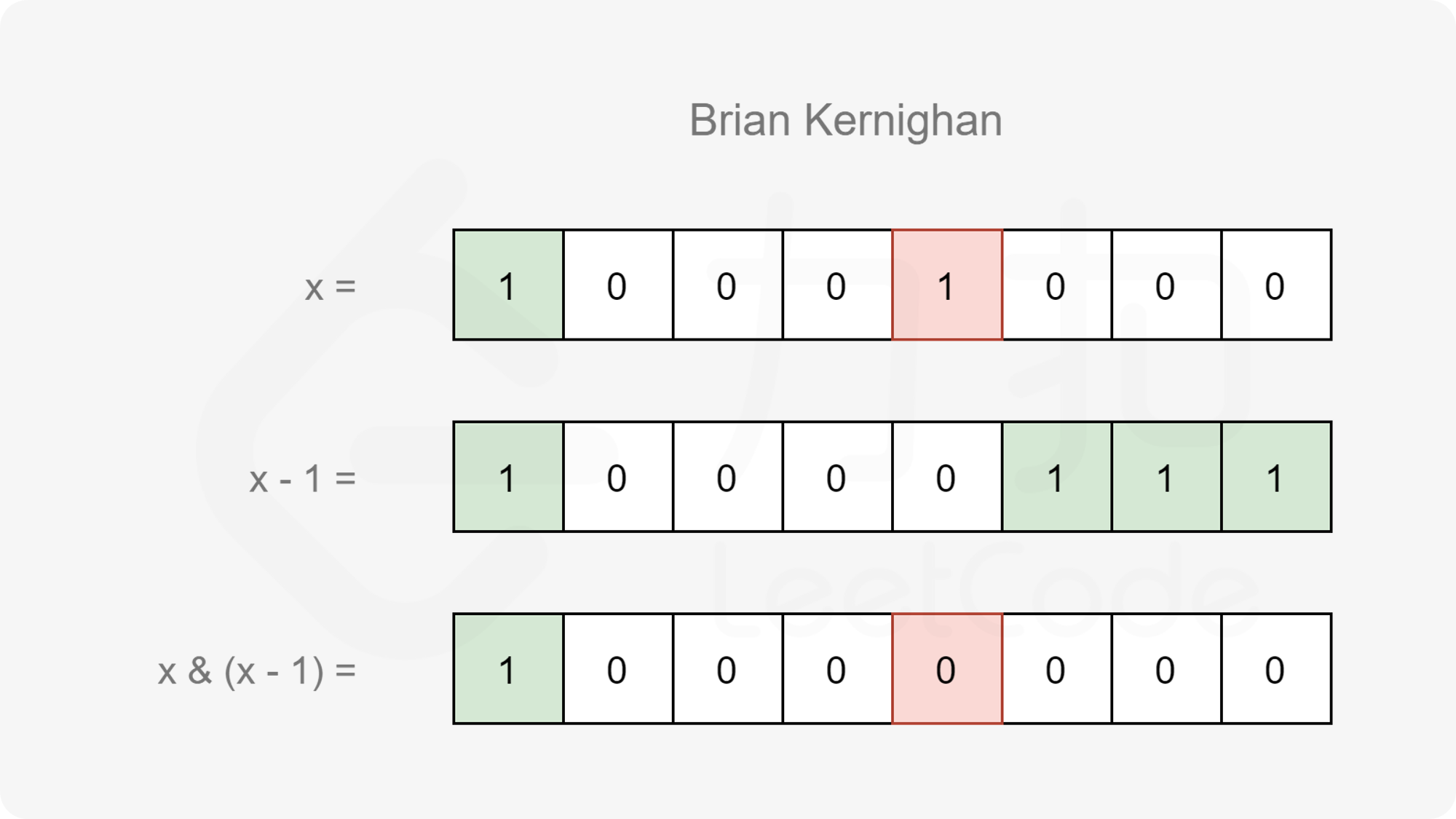
我们可以使用 Brian Kernighan 算法进行优化,具体地,该算法可以被描述为这样一个结论:记 f(x)f(x) 表示 x 和 x−1 进行与运算所得的结果(即 f(x)=x & (x−1)),那么 f(x) 恰为 x 删去其二进制表示中最右侧的 1 的结果。
基于该算法,当我们计算出 s=x⊕y,只需要不断让 s=f(s),直到 s=0 即可。这样每循环一次,s 都会删去其二进制表示中最右侧的 1,最终循环的次数即为 s 的二进制表示中 1 的数量。
注意:
0 ≤ x, y < 231.
示例:
输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置




