空间增强现实——基于贝塞尔曲面的异形表面投影变形技术
本博客不再继续更新,最新博客请转至:
https://blog.csdn.net/zzlyw/article/details/53215130
==================================================
1 空间增强现实投影
一般的投影是在平面、柱面或者球面屏幕上进行的。但是由于某些特殊的需求,需要在一些特殊的外形表面上进行投影,例如汽车表面、机器人表面或者其他一些工艺品等。这时仅仅从一个方向进行投影往往会有很多投影死角是不能被照亮的。所以需要从多个角度使用多个投影机进行工作。对于这种特殊的投影需求,投影的图像需要进行一些手动的变形以适应那些特殊的投影表面,以及不同投影图像之间的拼接。本文对最主要的贝塞尔变形过程进行介绍,并且附上源代码。
2 实现原理
在unity 3D中,可以生成一个网格,网格线的每一个交叉点都是三角面片的顶点,如图1所示。
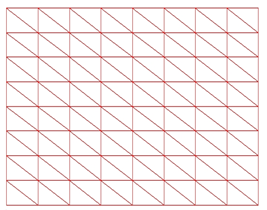
图1 网格控制示意图
然后将要投影的图像以纹理贴图的方式贴在网格上。此时,网格对应点已经和图像的像素点产生了映射关系。用户只需要控制网格顶点变动,其动作趋势就会被捕捉到,然后图像相应的映射点产生一致的位移。图中的每一个三角形面片都是一个图像单元。在图像区域人为生成一个控制点阵列(例如3*4),当某一个控制点移动时,其周围的三角面片顶点会依据距离远近进行不同程度的移动,这些三角面片也会随之发生形变。从全局角度看,所有的面片都发生着变化,进而使得贴附在网格面上的图像也发生着相应的变化。这一过程如图2所示。
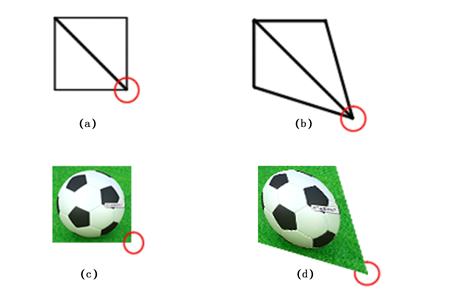
图2 图像随顶点变化示意图
这样一来,将控制点进行拖动,同时对照投影屏幕上的图像,就可以使图像的特定点达到指定的位置上。图1中网格记录的是图像的对应点的位置,一旦网格控制点的位置变化,对应的图像位置也会发生相应的变化,被拉伸的地方要进行插值,被压缩的地方进行抽样,为了使这种变换更加平滑,有必要采用一种适当的变形算法。
3 贝塞尔变形的实现
上面介绍的变形我们采用贝塞尔变形来完成。这种变形的特点在于,图像的每一个位置都是与所有的控制点的位置相关的,对于某一个选定的图像位置,离它越近的控制点被赋予越高的权重。因此,我们只需要调整控制点的位置,就可以控制图像进行变形了。并且这种变形是比较平滑的。(参考书:计算机图形学(第三版),Donald Hearn et al.)

图3 贝塞尔曲面
主要公式如下:
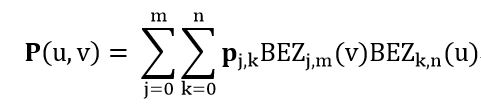
其中:
![]()

Bezier.cs 的主要代码如下:
using UnityEngine;
using System.Collections;
public class Bezier : MonoBehaviour {
Vector2[,] UV;
void Start () {
UV = new Vector2[GenerateController.sphere_m, GenerateController.sphere_n];
for (int i = 0; i < GenerateController.sphere_m; i++)
{
for(int j = 0; j < GenerateController.sphere_n; j++)
{
float _u = (float)j /( GenerateController.sphere_n -1);
float _v = (float)i /( GenerateController.sphere_m -1);
UV[i, j] = new Vector2(_u, _v);
// Debug.Log("uv: "+_u+" "+_v);
}
}
}
// Update is called once per frame
void Update () {
//to texture vertices
int total = GenerateController.sphere_m* GenerateController.sphere_n;
int index=0;
for (int i = 0; i < GenerateController.sphere_m; i++)
{
for (int j = 0; j < GenerateController.sphere_n; j++)
{
Vector3 _p = P(UV[i, j].x, UV[i, j].y);
GenerateController.Spheres[i, j].transform.position = _p;
}
}
for (int i = 0; i < GenerateController.sphere_m; i++)
{
for (int j = 0; j < GenerateController.sphere_n; j++)
{
MeshGeneration.vertices[index++] = GenerateController.Spheres[i, j].transform.position;
}
}
}
float Factorial(int n)
{
float product=1;
while(n!= 0)
{
product *= n;
n--;
}
return product;
}
float Combin(int n,int k)
{
if(n>=k)
{
float result = Factorial(n) / (Factorial(k) * Factorial(n - k));
return result;
}
else
{
return 0;
}
}
float BEZ(int k, int n, float u)
{
float result = Combin(n, k) * Mathf.Pow(u, k) * Mathf.Pow(1-u,n-k);
return result;
}
//compute the position of the point with (u,v) image coordinate
Vector3 P(float u,float v)
{
int m = GenerateController.m;
int n = GenerateController.n;
float tempX = 0;
float tempY = 0;
float tempZ = 0;
for (int j = 0; j < m; j++)
{
for (int k = 0; k < n; k++)
{
tempX += GenerateController.controlPoints[j, k].x * BEZ(j, m-1, v) * BEZ(k, n-1, u);
tempY += GenerateController.controlPoints[j, k].y * BEZ(j, m-1, v) * BEZ(k, n-1, u);
tempZ += GenerateController.controlPoints[j, k].z * BEZ(j, m-1, v) * BEZ(k, n-1, u);
}
}
return new Vector3(tempX,tempY,tempZ+5f);
}
}
实例实验结果如下所示。黄色的方块表示控制点的位置,可以使用鼠标拖动来改变位置。青色的小球显示了生成的网格的顶点位置,实际使用时候没有必要绘制出来。

图4 实验结果图
通过上面的简单介绍,相信你已经对于贝塞尔曲面有了初步的认识。可以利用给出的代码扩展自己的工程,将变形功能加入到现有的程序中了。




