基本算法
常用排序介绍
- 插入排序法:直接插入排序,希尔排序
- 交换排序:冒泡排序,快速排序
- 选择排序:直接选择排序,堆排序
- 归并排序: 归并排序
- 基数排序
二分查找
public static void main(String[] args) {
int[] para = {1,2,3,4,5,6,7,8,9,10,11};
System.out.println(binarySearch(para,8,0));
}
/***
* 用数组中间位置(length/2)的值和查找的值比较,如果目标值大,然后用数组后半段继续折半比较
* @param para 查找数组
* @param target 要查找的目标值
* @param count 查找次数
* @return
*/
public static int binarySearch(int[] para,int target,int count){//8
count++;
if(para.length<=1){
return count;
}
//先判断奇偶数
if(para.length%2 > 0){//奇数
int subNum = para.length/2;//2
if(target == para[subNum]){
return count;
}else if(target>para[subNum]){
count = binarySearch(subArray(para,subNum,para.length),target,count);
}else if(target<para[subNum]){
count = binarySearch(subArray(para,0,subNum),target,count);
}
}else{//偶数
int subNum = para.length/2;//2
if(target == para[subNum]){
return count;
}else if(target>para[subNum]){
count = binarySearch(subArray(para,subNum,para.length),target,count);
}else if(target<para[subNum]){
count = binarySearch(subArray(para,0,subNum),target,count);
}
}
return count;
}
private static int[] subArray(int[] para,int beginIndex,int endIndex){//4,8
int[] result = new int[endIndex-beginIndex-1];
int index = 0;
for(int i=beginIndex+1;i<endIndex;i++){
result[index] = para[i];
index++;
}
return result;
}
快速排序
特点:适合大数据量,元数据基本无序
package com.longfor.ads2.Test;
import java.util.Arrays;
public class QuickSort {
/***
* 快速排序
* 每次把数组分割成左右两半,然后通过递归,分别在调用排序方法
*/
public static void main(String[] args) {
int[] para = {5,2,1,1,8,9,8,67,3,4,5,6,2,7,0};
quickSort(para,0,para.length-1);
System.out.println(Arrays.toString(para));
}
private static void quickSort(int[] para,int leftIndex,int rightIndex){
if(leftIndex<rightIndex){
int kIndex = doSort(para,leftIndex,rightIndex);
quickSort(para,leftIndex,kIndex-1);
quickSort(para,kIndex+1,rightIndex);
}
}
private static int doSort(int[] para,int leftIndex,int rightIndex){
int kValue = para[leftIndex];//坑的值
int kIndex = leftIndex;//坑的索引
int kRedirect = 0;//坑的方向
while (leftIndex<rightIndex){
if(kRedirect==0){//坑在左边,和右边比较
if(kValue>para[rightIndex]){//需要替换
swap(para,kIndex,rightIndex);
leftIndex++;
kIndex = rightIndex;
kRedirect++;
}else{
rightIndex--;
}
}else{
if(kValue<para[leftIndex]){//需要替换
swap(para,kIndex,leftIndex);
rightIndex--;
kIndex = leftIndex;
kRedirect--;
}else{
leftIndex++;
}
}
}
return kIndex;
}
private static void swap(int[] para,int index1,int index2){
int tmp = para[index1];
para[index1] = para[index2];
para[index2] = tmp;
}
}
冒泡排序
public static void main(String[] args) {
int[] bubbleSort = {3,2,5,9,3,6,10,22};
int[] bubbleSort2 = bubbleSort(bubbleSort);
for(int tmp:bubbleSort2){
System.out.println(tmp);
}
}
/***
* 冒泡排序
* 32593
*
* 23593
* 23593
* 23593
* 23539
*
* 23539
* 23539
* 23359
*
* 23359
* 23359
*
*
* 两个优化点:
* 1、如果序列大部分都是有序的数据,少部分需要排序,那么如果某次排序的时候没有发生数据交换,则可以认为序列已经排序完毕
* 2、假设序列有1000个数据,后900个都是有序的并且都比前100个数据大,则每次排序只需要比较到前100
*
*/
public static int[] bubbleSort(int[] para){
int length = para.length;
int flag2 = 0;//记录最后一次交换的位置,那么后续遍历,这个位置后的数据不需要进行排序
for(int i=0;i<length-2;i++){
boolean flag = true;
for(int j=0;j<length-i-1;j++){
if(j<flag2){
int a = para[j];
int b= para[j+1];
if(a>b){
para[j]=b;
para[j+1]=a;
flag=false;
flag2= j;
}
}
}
if(flag){//优化1:如果序列本身大部分数据都是有序的,则某一次排序没有发生交换,证明全部排序已经完毕
return para;
}
}
return para;
}
二叉树
二叉树每个节点都大于左子节点,小于右子节点。
平衡二叉树
二叉树进行更新操作后可能导致不平衡:如图,插入10后,11节点左边高度为3,右边为1,差大于1了。就要对树进行旋转使树保持平衡。
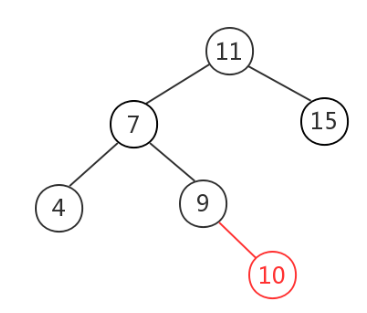
旋转分4种情况:
如图:观察发现失衡的节点为10,新插入的节点是5,5处于10的左子节点(7)的左子节点(4)下边,这种情况叫做左左。
依次还有左右、右左、右右
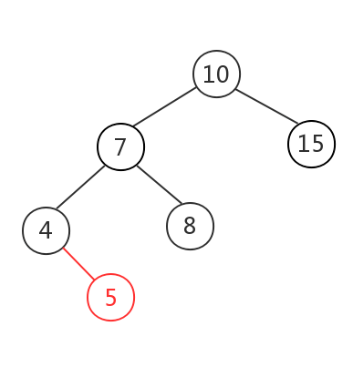
左左:右旋
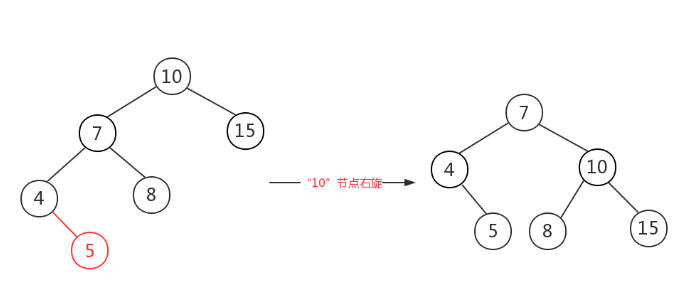
左右:先对7进行左旋,树变成左左树了,然后对11进行右旋
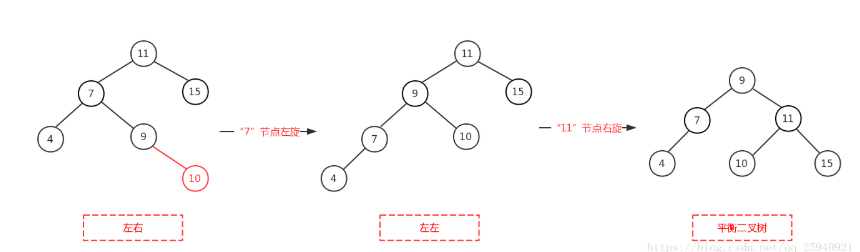
右右和右左同理。
删除
上面将的是新增节点之后通过旋转维持平衡。
删除相对插入要复杂一些。
(1)当删除的节点是叶子节点,则将节点删除,然后从父节点开始,判断是否失衡,如果没有失衡,则再判断父节点的父节点是否失衡,直到根节点,此时到根节点还发现没有失衡,则说此时树是平衡的;如果中间过程发现失衡,则判断属于哪种类型的失衡(左左,左右,右左,右右),然后进行调整。
(2)删除的节点只有左子树或只有右子树,这种情况其实就比删除叶子节点的步骤多一步,就是将节点删除,然后把仅有一支的左子树或右子树替代原有结点的位置,后面的步骤就一样了,从父节点开始,判断是否失衡,如果没有失衡,则再判断父节点的父节点是否失衡,直到根节点,如果中间过程发现失衡,则根据失衡的类型进行调整。
(3)删除的节点既有左子树又有右子树,这种情况又比上面这种多一步,就是中序遍历,找到待删除节点的前驱或者后驱都行,然后与待删除节点互换位置,然后把待删除的节点删掉,后面的步骤也是一样,判断是否失衡,然后根据失衡类型进行调整。
遍历
前序:根 - 左 - 右
中序:左 - 根 - 右
后续:左 - 右 - 根
234树
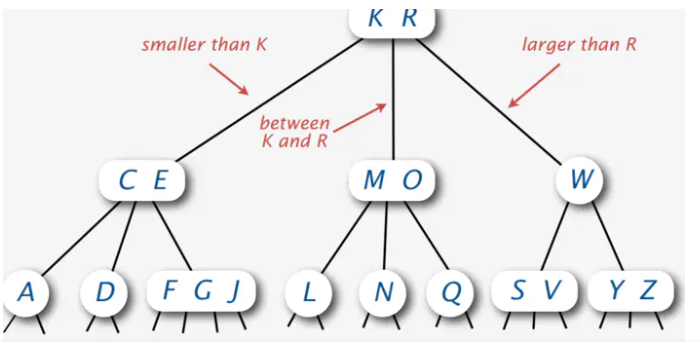
如图中:
W节点叫2-node
MO节点叫3-node
FGL节点叫4-node
插入
新插入的数据总是插入到叶子节点上。
插入都是先从根节点开始往下找,遇到3节点进行分裂,最终定位到叶子节点插入。
向2-node插入数据后,2-node就变为3-node,同理3-node变4-node。
但是当向4-node插入数据后,因为4-node无法继续升级,所以就需要分裂。
通常我们会将 4-node中中间的元素,放到它的父节点中,并进行分裂。

分裂是向上分裂的,如果根节点也是4-node怎么办?
这个时候也是继续向上分裂,只不过需要创建新的根节点。
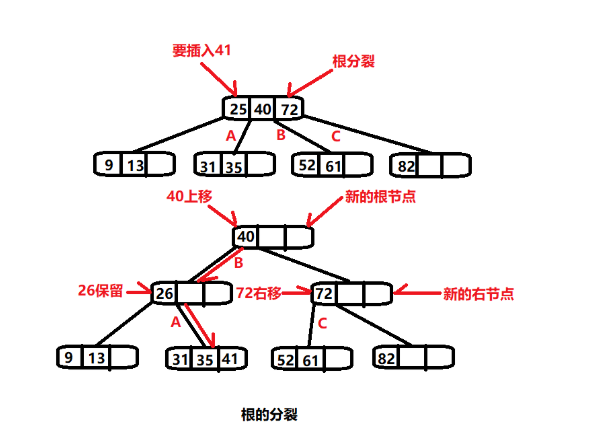
删除
1、如果2-3-4树中不存在当前需要删除的key,则删除失败。
2、如果当前需要删除的key不位于叶子节点上,则用后继key覆盖,然后在它后继key所在的子支中删除该后继key。
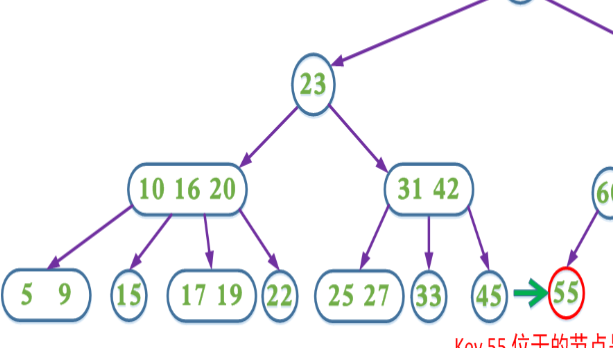
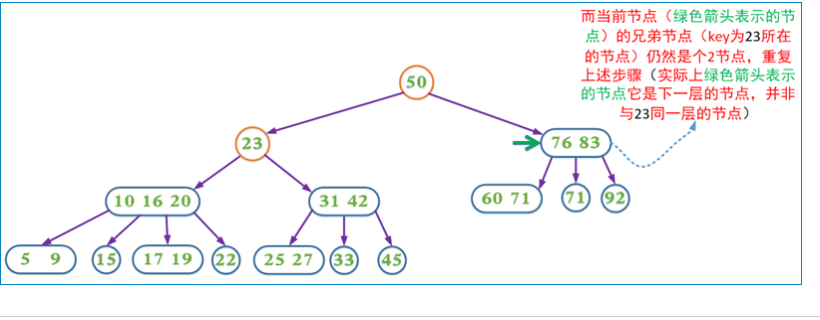
什么是后继key?如图,10的后继key就是9。
3、如果当前需要删除的key位于叶子节点上,并且不是2-node,直接删除即可
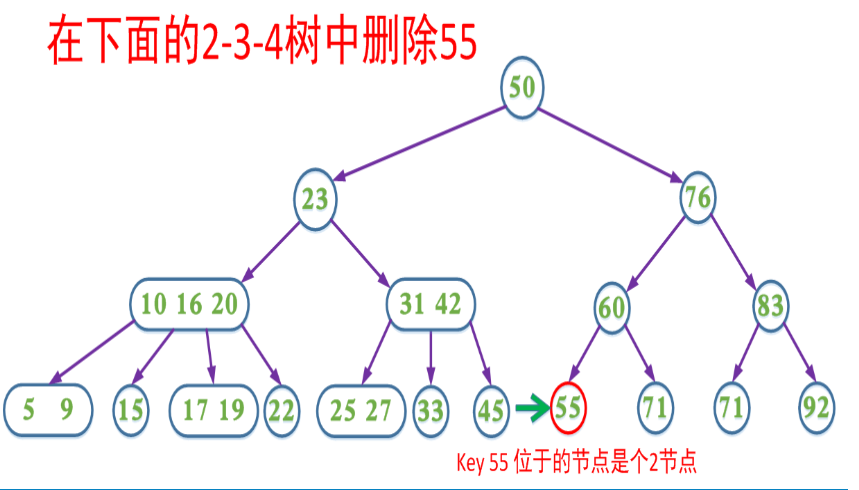
4、如果当前需要删除的key位于叶子节点上,并且是2-node。又分三种情况
1、如果兄弟节点不是2节点,则父节点中的key下移到该节点,兄弟节点中的一个key上移
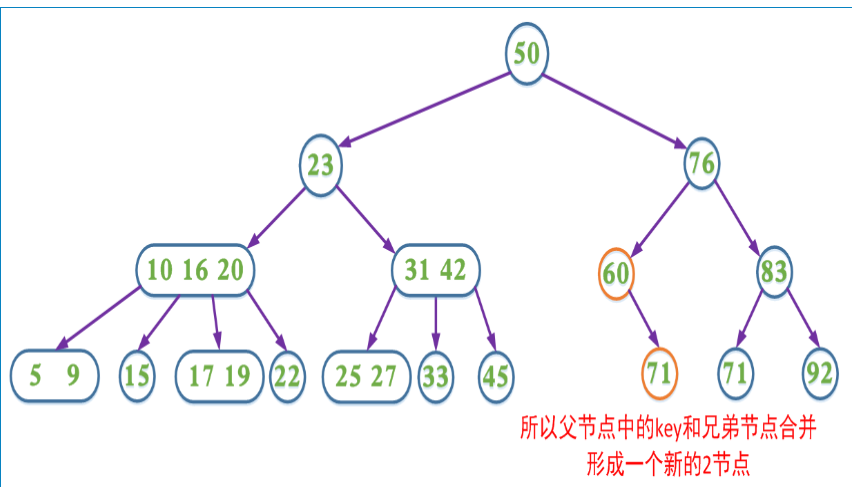
2、如果兄弟节点是2节点,父节点是个3节点或4节点,父节点中的key与兄弟节点合并
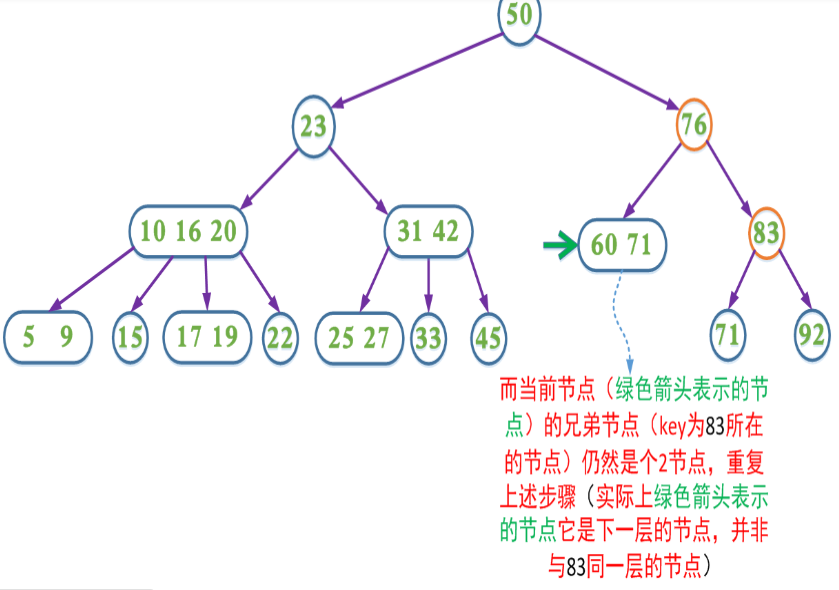
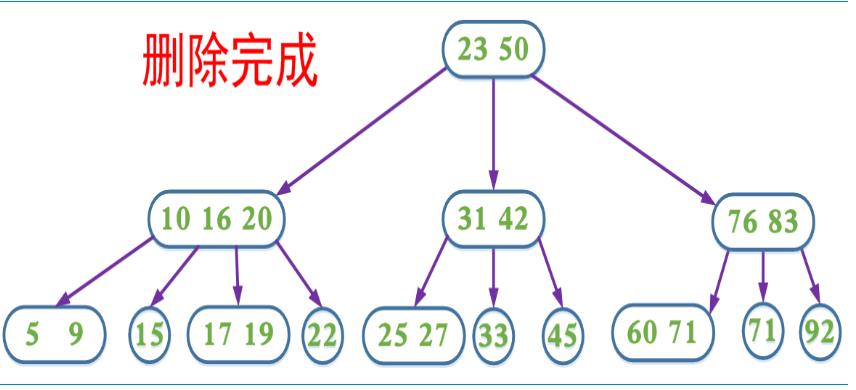
3、如果兄弟节点是2节点,父节点是个2节点,父节点中的key与兄弟节点中的key合并,形成一个3节点,把此节点看成当前节点(此节点实际上是下一层的节点),重复步骤步骤1和2
第4种情况分析如图:
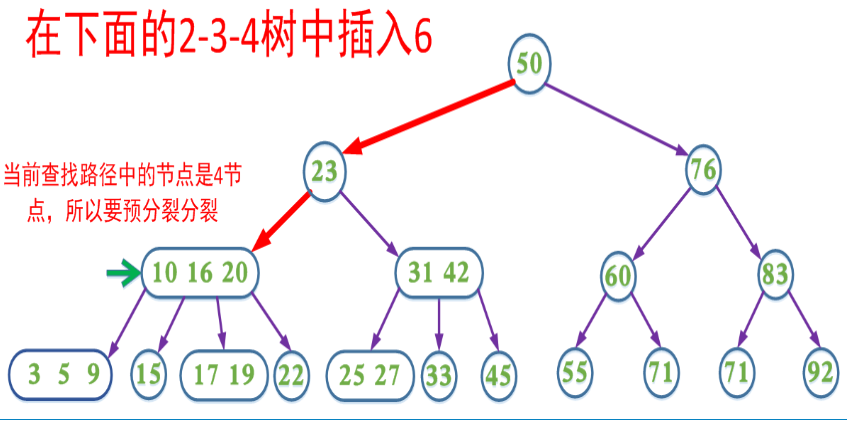
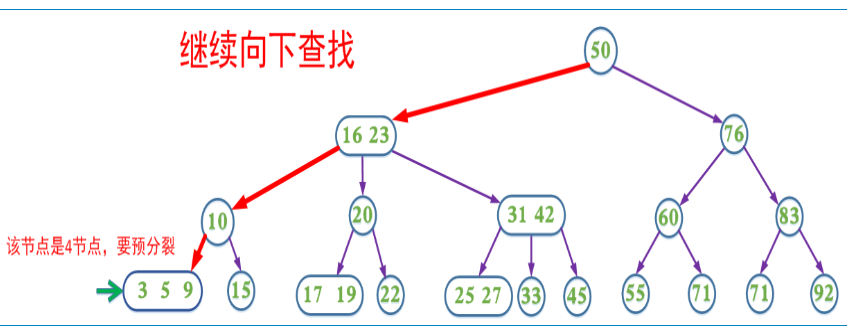
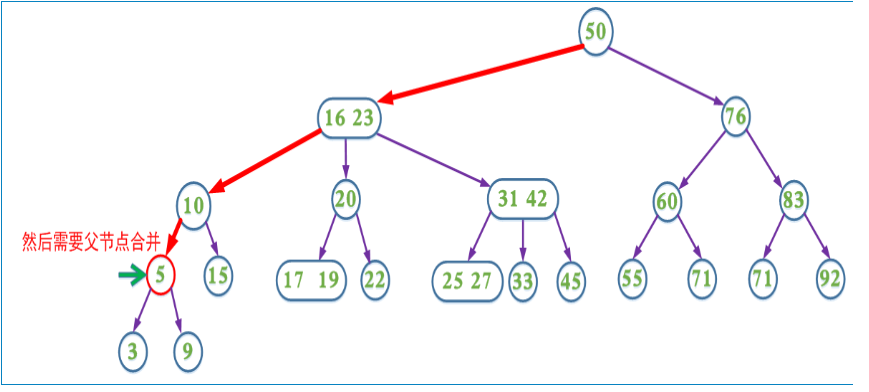
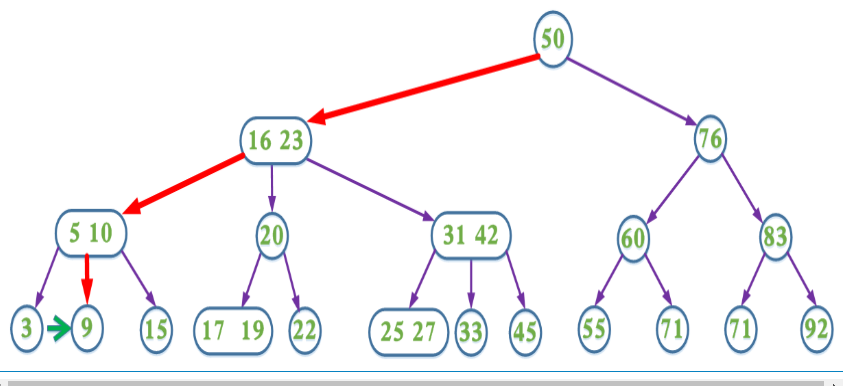
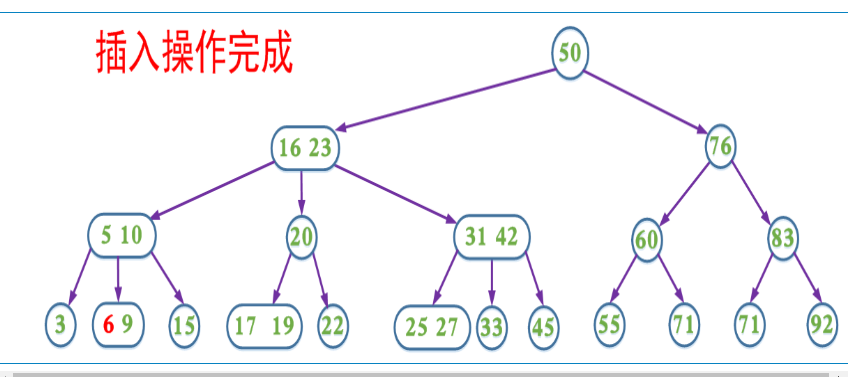
带有预分裂的插入操作
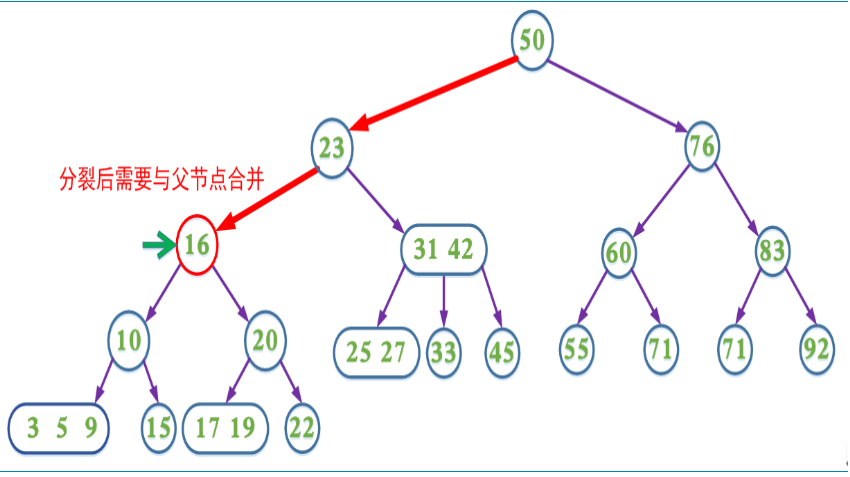
上面的插入以及删除操作在某些情况需要不断回溯来调整树的结构以达到平衡。为了消除回溯过程,在插入操作过程中我们可以采取预分裂的操作,即我们在插入的搜索路径中,遇到4节点就分裂(分裂后形成的根节点的key要上移,与父节点中的key合并)这样可以保证找到需要插入节点时可以直接插入(即该节点一定不是4节点)。
提前分裂,减少回溯的的查找过程。
带有预合并的删除操作
在删除过程中,我们同样可以采取预合并的操作,即我们在删除的搜索路径中(除根节点,因为根节点没有兄弟节点和父节点),遇到当前节点是2节点,如果兄弟节点也是2节点就合并(该节点的父节点中的key下移,与自身和兄弟节点合并);如果兄弟节点不是2节点,则父节点的key下移,兄弟节点中的key上移。这样可以保证,找到需要删除的key所在的节点时可以直接删除(即要删除的key所在的节点一定不是2节点)。
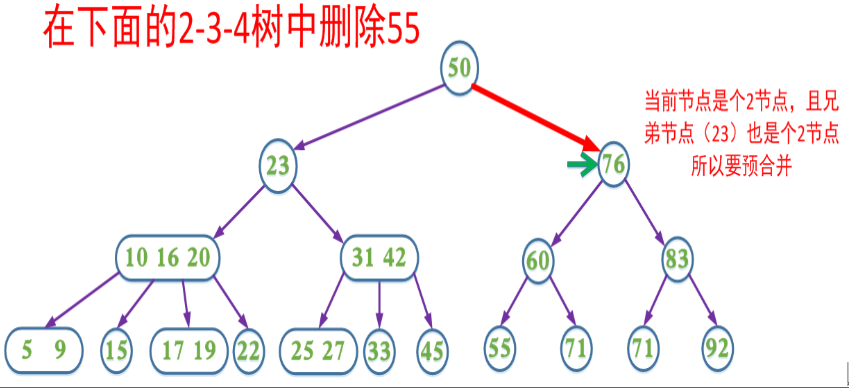

这里包含key为60的节点也可以选择让父节点中的key 76下移和兄弟节点中的83合并,两种方式都能达到B树的平衡,这也是在2-3-4树对应的红黑树中使用的方式。
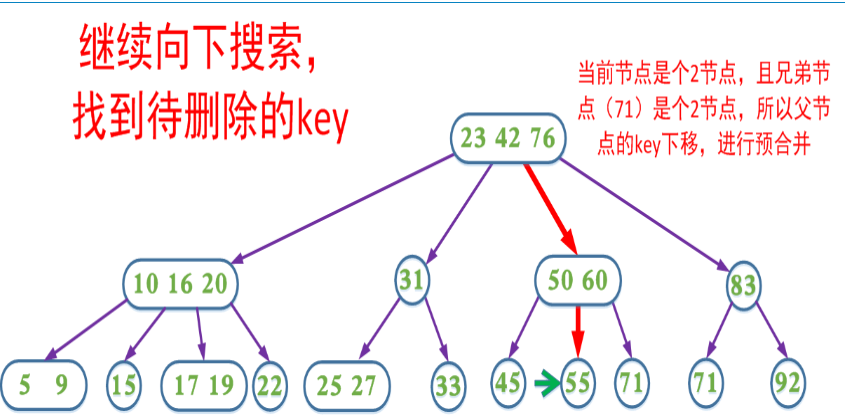
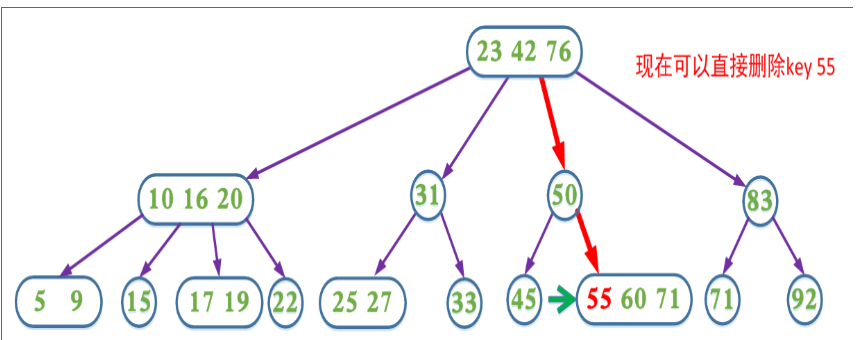
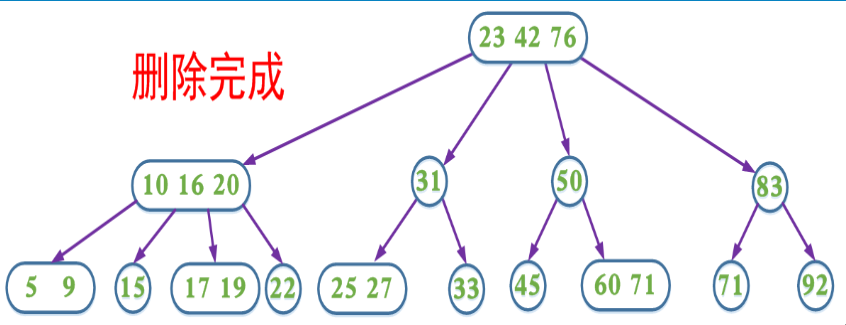
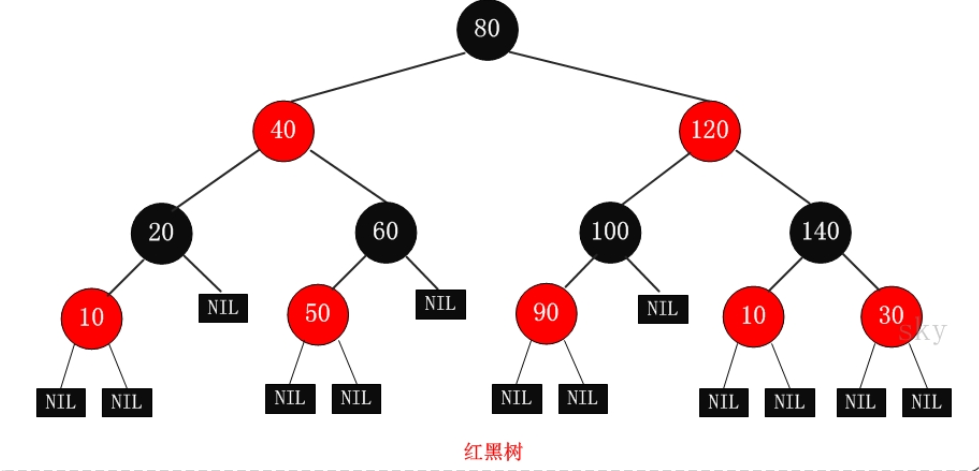
红黑树
二叉树删除节点的时候,都要遍历到根节点来判断是否失衡,这样效率很低,红黑树通过给节点增加颜色属性来解决此问题。
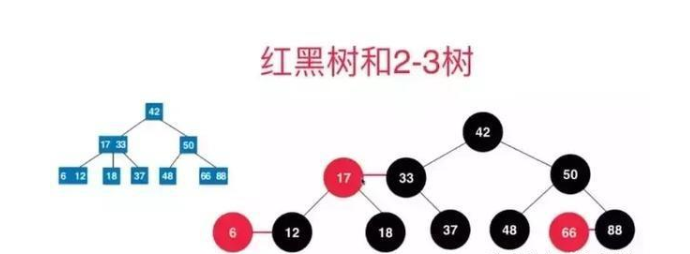
从上面可以看到,把红色节点放到与父亲齐平,就是2-3树中的一个2-3节点。
红黑树是以空间换时间来减少查询复杂度的数据结构,有以下几种特性:
1、根节点为黑色
2、所有叶子节点为黑色(叶子节点都是不存储数据的如下图)
3、如果一个节点为红色,则它的子节点一定为黑色
4、任意一结点到每个叶子结点的路径都包含数量相同的黑结点。(.红黑树是完美黑色平衡)
当更新操作的时候,上面4种特性可能被破坏,破坏之后要通过颜色调整和旋转来满足上面4个规则。
只要满足上面的条件,就能保证任意节点的最大深度不会超过最小深度两倍(树的深度不会过于失衡)。
旋转选择同二叉树一样
查找同二叉树一样
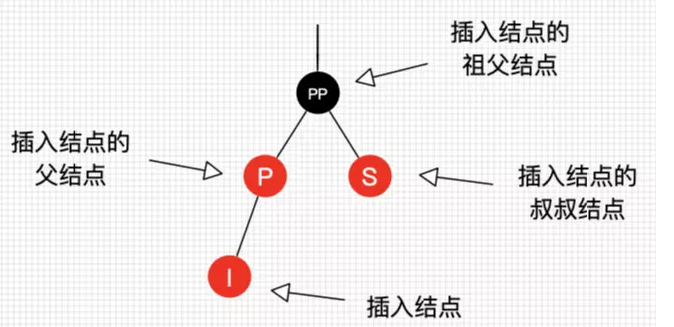
插入
插入第一步是找到要插入的位置,插入节点,然后判断是否打乱红黑树特性了,如果打乱要进行调整(通过改变节点颜色和旋转来实现)。
那么假设我们在最底部插入元素,肯定是想要插入一个红色结点,这样,树的高度实际上没有任何变化,而插入黑结点使得高度+1。所以插入的节点必定是红色(根节点除外)。

堆
可以把堆看作一个数组,也可以被看作一个完全二叉树,通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组
按照堆的特点可以把堆分为大顶堆和小顶堆:
大顶堆:每个结点的值都大于或等于其左右孩子结点的值
小顶堆:每个结点的值都小于或等于其左右孩子结点的值
堆常常被当做优先队列使用,因为可以快速的访问到“最重要”的元素
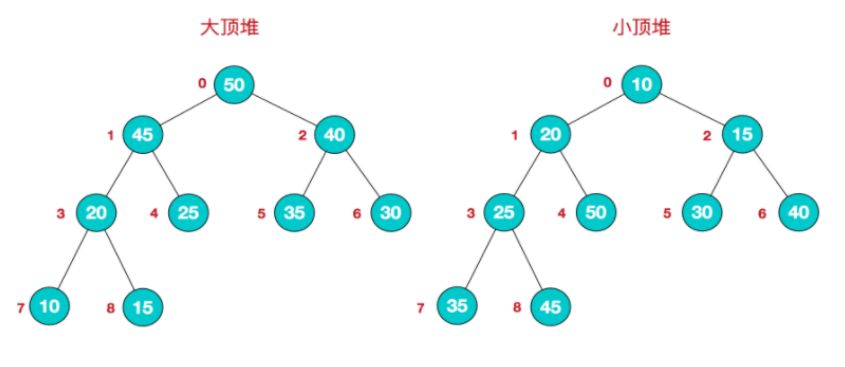
我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子

我们用简单的公式来描述一下堆的定义就是:(可以对照上图的数组来理解下面两个公式)
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
堆排序怎么实现?
比如说有个初始数组:
int[] a = {7,3,8,5,1,2};
排序之前堆如下图
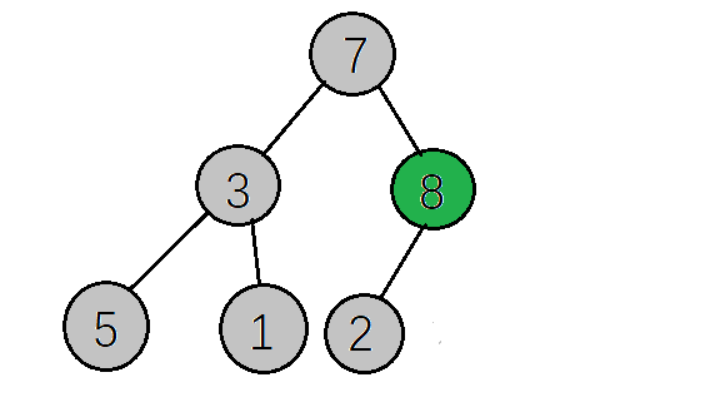
通过堆排序实现小顶堆(正序),思路如下:
内层循环:
1、首先找到8位置节点(length/2 - 1),拿着该节点与其子节点(包含左右)分别比较,一旦该节点小于子节点,则替换。
2、接下来比较3节点(8节点 -1),逻辑同上
3、以此类推,第一次遍历后会拿到一个最大值到顶点,因为是正序,所以将顶点与尾点替换。
这样一次循环完毕后,尾节点就遍历出一个最大值。
外层循环:
4、接下来继续循环上面的逻辑,每次循环去掉已经遍历出的尾部节点。
代码实现:
public static void main(String[] args) {
int[] a = {7,3,8,5,1,2};
heapSort(a);
for(int x:a){
System.out.println(x);
}
}
public static void heapSort(int[] a){
for(int j=0;j<a.length;j++){
int length = a.length - j;//外层循环,每次尾部已经遍历过的去掉
for(int i=length/2 - 1;i>=0;i--){
int leftSon = 2*i + 1;//5
int rightSon = leftSon + 1;//6
if(leftSon < length && a[i] < a[leftSon]){
swap(a,i,leftSon);
}
if(rightSon < length && a[i] < a[rightSon]){
swap(a,i,rightSon);
}
}
//首尾替换
swap(a,0,length-1);
}
}
private static void swap(int[] a,int index1,int index2){
int tmp = a[index1];
a[index1] = a[index2];
a[index2] = tmp;
}
跳表
在单链表中查询一个元素的时间复杂度为O(n),即使该单链表是有序的,我们也不能通过2分的方式缩减时间复杂度。

如上图,我们要查询元素为55的结点,只需要在L2层查找4次即可。在这个结构中,查询结点为46的元素将耗费最多的查询次数5次。即先在L2查询46,查询4次后找到元素55,因为链表是有序的,46一定在55的左边,所以L2层没有元素46。然后我们退回到元素37,到它的下一层即L1层继续搜索46。非常幸运,我们只需要再查询1次就能找到46。这样一共耗费5次查询。
限流
1.漏桶
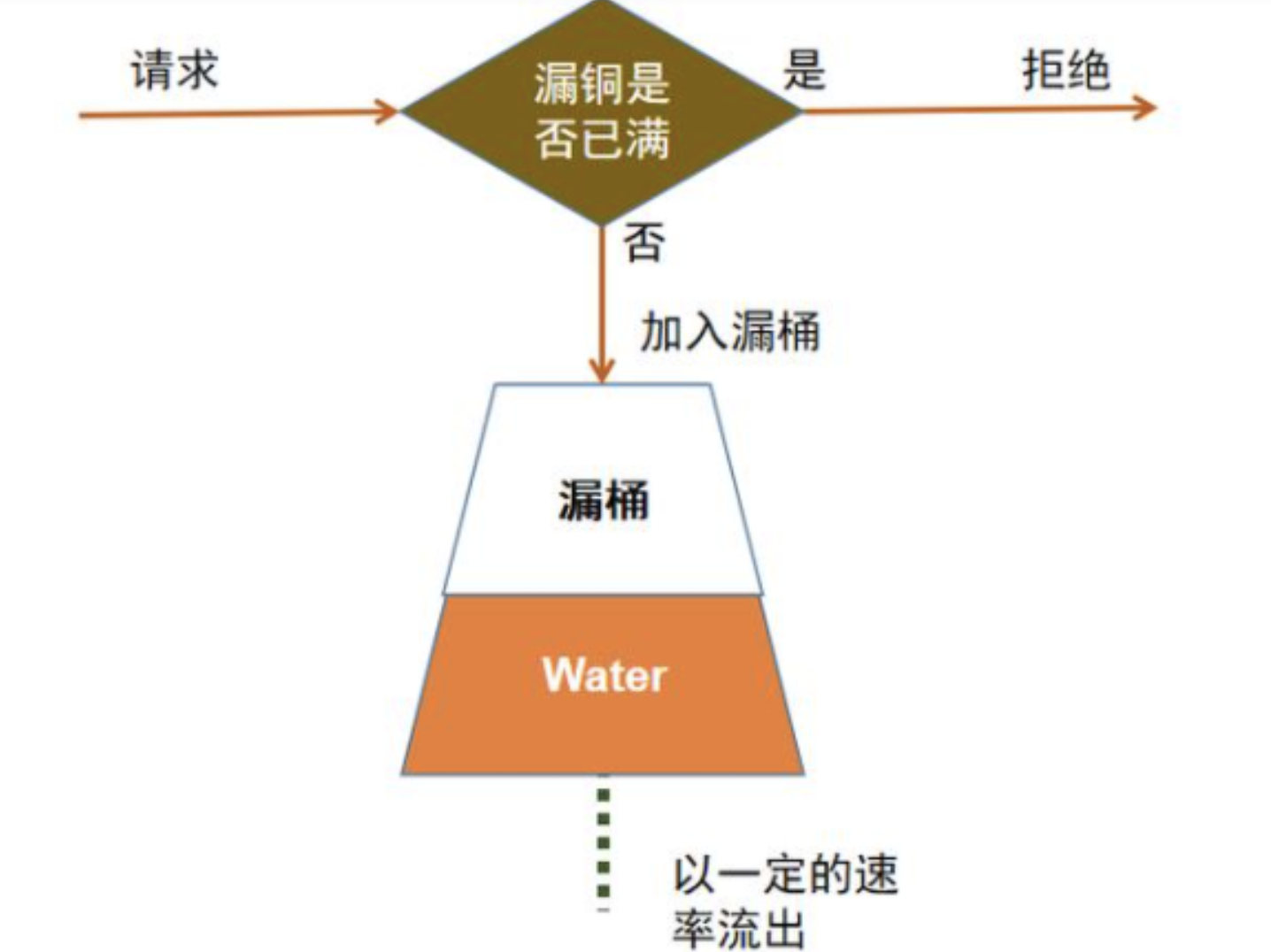
1、定义这个桶的最大容量;
2、记录好上次操作完成后的时间以及桶的剩余量,用来记录后续计算当前桶的容量;
3、定义好流速,速率越小,流控越大,流量越小;
4、每次请求,需要先检查桶大小,如果超过最大值,则拒绝,如果没有超过最大值则继续进行操作
'''java
public class LeakyBucket {
// 流出速率
private double rate;
// 桶大小
private double burst;
// 最后更新时间
private long refreshTime;
// 现有量
private int water;
public LeakyBucket(double rate,double burst){
this.rate = rate;
this.burst = burst;
}
/**
* 用来刷新水量
*/
private void refreshWater(){
long now = System.currentTimeMillis();
water = (int) Math.max(0,water-(now-refreshTime)* rate);
refreshTime = now;
}
public synchronized boolean tryAcquire(){
refreshWater();
if (water<burst) {
water++;
return true;
}else {
return false;
}
}
private static LeakyBucket leakyBucket = new LeakyBucket(1,100);
public static void main(String[] args) {
ExecutorService executorService = Executors.newCachedThreadPool();
for (int i = 0; i < 1000; i++) {
executorService.execute(()->{
System.out.println(leakyBucket.tryAcquire());
});
}
executorService.shutdown();
}
}
'''
令牌桶
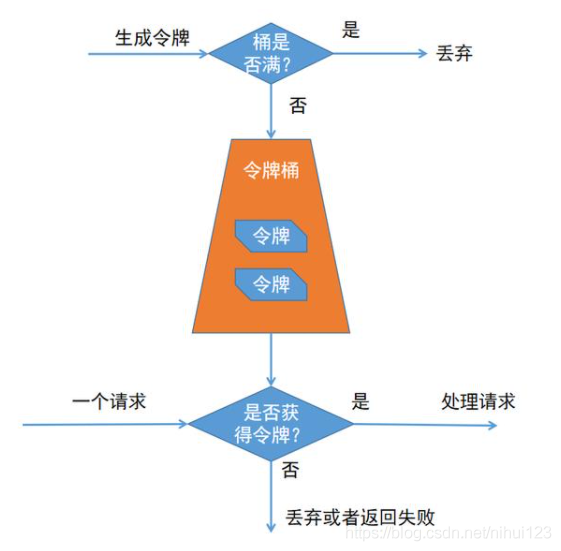
'''java
public class TokenLimiter {
private ArrayBlockingQueue<String> blockingQueue;
private int limit;
private TimeUnit timeUnit;
private int period;
public TokenLimiter(int limit,int period,TimeUnit timeUnit){
this.limit = limit;
this.timeUnit = timeUnit;
this.period = period;
blockingQueue = new ArrayBlockingQueue<>(limit);
init();
start();
}
/**
* 初始化令牌操作
*/
private void init() {
for (int i = 0; i < limit; i++) {
blockingQueue.add("1");
}
}
/**
* 获取令牌为空,返回false
* @return
*/
public boolean tryAcquire(){
return blockingQueue.poll()==null?false:true;
}
private void addToken(){
blockingQueue.offer("1");
}
private void start() {
Executors.newScheduledThreadPool(1).scheduleAtFixedRate(()->{
addToken();
},10,period,timeUnit);
}
}
'''
区别:
漏桶:保护别人系统
令牌桶:保护自己系统
dfs
1、初始化固定数量的令牌放入令牌桶中
2、初始化和开启一个定时任务,定时往令牌桶添加令牌
3、提供一个获取令牌的方法,获取一个令牌,令牌桶中减一,如果令牌桶为空,则返回失败