[Leetcode] Implement strStr()
Implement strStr() 题解
题目来源:https://leetcode.com/problems/implement-strstr/description/
Description
Implement strStr().
Return the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack.
Example
Example 1:
Input: haystack = "hello", needle = "ll"
Output: 2
Example 2:
Input: haystack = "aaaaa", needle = "bba"
Output: -1
Solution
class Solution {
public:
int strStr(string haystack, string needle) {
if (needle.empty())
return 0;
int hi = 0, ni = 0;
int hsize = haystack.size(), nsize = needle.size();
int temp = 0;
while (hi < hsize && ni < nsize) {
if (haystack[hi] != needle[ni]) {
if (ni > 0)
hi = temp;
hi++;
ni = 0;
} else {
if (ni == 0)
temp = hi;
hi++;
ni++;
}
}
return (ni == nsize) ? hi - nsize : -1;
}
};
解题描述
这道题题意是在给出的字符串haystack中查找子串needle,若存在则返回第一个匹配的起始位置下标,否则返回-1。上面的解法使用的是暴力破解,从头开始匹配,如果在匹配到中间时匹配失败则haystack的游标hi回退到之前开始匹配的位置temp,needle的游标ni回退到0。
暴力破解的低效原因
当然了,上述暴力解法肯定是不够高效的。比如给出例子:
上面的字符串为haystack,下面的为needle,可以看到此时needle的最后一个字母不匹配。按照上面暴力破解的做法,此时应该将ni回退到开始位置,即:
但是我们可以发现,其实没有必要回退这么多,只需要回退一部分,因为之前已经匹配的那部分串ABCDAB的后缀AB刚好是needle的前缀;并且haystack的游标hi完全不需要回退,即:
那问题的关键就是,如何计算出回退的步长。当我们能够计算出在所有已匹配长度的情况下需要回退的步长就可以在很大程度上减少回退的量,从而实现一个高效的子字符串匹配算法,这个算法就是经典的KMP算法。
KMP算法
KMP算法中把上面提到的每种已匹配的长度情况下对应需要回退的步长构成的一个数组称为next数组。上文提到,next数组对应的性质就是needle串中前缀与 后缀中的一部分(上文例子中"ABCDAB"是needle的前缀子串,其后缀"AB"与needle的前缀相同,"AB"只能算是needle后缀的一部分,而不是网上其他很多博客讲到的后缀) 相同的情况,求next数组就是要求前缀和后缀的一部分所能匹配的最长长度。
对needle = "ABCDABD",我们可以得到这样的数据:
| needle的各个前缀串 | 前缀串的前缀 | 前缀串的后缀 | 最大公共元素长度 |
|---|---|---|---|
| A | 无 | 无 | 0 |
| AB | A | B | 0 |
| ABC | A,AB | C,BC | 0 |
| ABCD | A,AB,ABC | D,CD,BCD | 0 |
| ABCDA | A,AB,ABC,ABCD | A,DA,CDA,BCDA | 1 |
| ABCDAB | A,AB,ABC,ABCD,ABCDA | B,AB,DAB,CDAB,BCDAB | 2 |
| ABCDABD | A,AB,ABC,ABCD,ABCDA,ABCDAB | D,BD,ABD,DABD,CDABD,BCDABD | 0 |
表格中的”最大公共元素长度“就是我们求next数组关键的数据。
| needle | A | B | C | D | A | B | D |
|---|---|---|---|---|---|---|---|
| 最大公共元素长度 | 0 | 0 | 0 | 0 | 1 | 2 | 0 |
求next数组
不难看出,当ni = i时出现不匹配,ni应该退到i + 1对应的位置上的”最大公共元素长度“对应的位置。也就是说next相当于把上面的”最大公共元素长度“表格整体右移一位,初值赋值为-1:
| needle | A | B | C | D | A | B | D |
|---|---|---|---|---|---|---|---|
| next | -1 | 0 | 0 | 0 | 0 | 1 | 2 |
计算过程写成代码就是:
void genNext(string& str) {
int size = str.size();
next = new int[size];
memset(next, 0, sizeof(next));
int k = -1;
int j = 0;
next[0] = -1;
while (j < size - 1) {
// k代表”前缀“游标,j代表”后缀“游标
if (k == -1 || str[k] == str[j]) {
k++;
j++;
next[j] = k;
} else {
// ”前缀“与”后缀“出现不匹配,同理进行回退
k = next[k];
}
}
}
next数组优化
但是这里还是存在问题,先看一个例子:
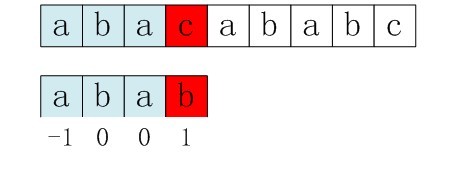
可以看到,在b这个字母上出现不匹配,按照上述算法计算出来的next = [-1, 0, 0, 1]即要回退到下面的状态:
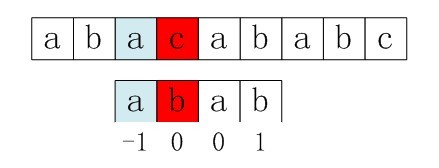
但是显然,红色的c和b是不匹配,需要再次进行回退。这就降低了算法的效率。而问题的根源在于,前面的图中needle游标在b字符上不匹配,当然如果回退之后起始位置仍然是b肯定不匹配,所以在计算next数组的时候不能允许这种情况的出现,而应该递归回退到与当前不匹配字符不相等的时候,即:
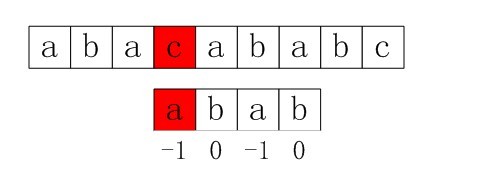
优化后的next计算算法为:
void genNext(string& str) {
int size = str.size();
next = new int[size];
memset(next, 0, sizeof(next));
int k = -1;
int j = 0;
next[0] = -1;
while (j < size - 1) {
// k代表”前缀“游标,j代表”后缀“游标
if (k == -1 || str[k] == str[j]) {
k++;
j++;
// 过滤掉相等的情况,递归回退到不相等的时候,避免二次回退
if (str[k] == str[j])
next[j] = next[k];
else
next[j] = k;
} else {
// ”前缀“与”后缀“出现不匹配,同理进行回退
k = next[k];
}
}
}
完整的算法为:
class Solution {
private:
int *next;
void genNext(string& str) {
int size = str.size();
next = new int[size];
memset(next, 0, sizeof(next));
int k = -1;
int j = 0;
next[0] = -1;
while (j < size - 1) {
// k代表”前缀“游标,j代表”后缀“游标
if (k == -1 || str[k] == str[j]) {
k++;
j++;
// 过滤掉相等的情况,递归回退到不相等的时候,避免二次回退
if (str[k] == str[j])
next[j] = next[k];
else
next[j] = k;
} else {
// ”前缀“与”后缀“出现不匹配,同理进行回退
k = next[k];
}
}
}
public:
int strStr(string haystack, string needle) {
if (needle.empty())
return 0;
genNext(needle);
int hi = 0, ni = 0;
int hsize = haystack.size(), nsize = needle.size();
int temp = 0;
while (hi < hsize && ni < nsize) {
if (ni == -1 || haystack[hi] == needle[ni]) {
hi++;
ni++;
} else {
ni = next[ni];
}
}
delete [] next;
return (ni == nsize) ? hi - nsize : -1;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号