树状数组入门

                今天来讨论下树状数组

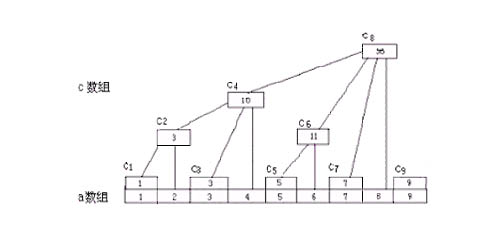
                先把这幅图和些它的理论概念直接从百度上拽过来，后面再谈谈我对它的一些理解

 

              来观察这个图：

　　      令这棵树的结点编号为C1，C2...Cn。令每个结点的值为这棵树的值的总和（就是c[n]表示数组a从第一项一直加到n项的和，比如C4，它就是c[4]=a[1]+a[2]+a[3]+a[4]=10,和图中所存数据相同），那么容易发现：

     　　C1 = A1

　    　C2 = A1 + A2

　　    C3 = A3

　　   C4 = A1 + A2 + A3 + A4

　　   C5 = A5

　　   C6 = A5 + A6

　　   C7 = A7

　　   C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

           .......

          从图中不难发现,c[k]存储的实际上是从k开始向前数k的二进制表示中右边第一个1所代表的数字个元素的和(这么说可能有点拗口,令lowbit为k的二进制表示中右边第一个1所代表的数字,然后c[k]里存的就是从a[k]开始向前数lowbit个元素之和)

 这么存有什么好处呢?无论是树状数组还是线段树,都用到了分块的思想,而树状数组采用这样的存储结构我想最主要的还是这样方便计算,我们可以用位运算轻松地算出lowbit.分析一下这样做的复杂度:对于更改元素来说,如果第i个元素被修改了,因为我们最终还是要求  和,    所以可以直接在c数组里面进行相应的更改,如图中的例子,假设更改的元素是a[2],那么它影响到得c数组中的元素只有c[2],c[4],c[8],我们只需一层一层往上修改就可以了,这个过程的最坏的复杂度也不过O(logN);对于查找来说,如查找s[k],只需查找k的二进制表示中1的个 数次就能得到最终结果,比如查找s[7],7的二进制表示中有3个1,也就是要查找3次,到底是不是呢,我们来看上图,s[7]=c[7]+c[6]+c[4],可能你还不知道怎么实现这个过程.

还以7为例,二进制为0111,右边第一个1出现在第0位上,也就是说要从a[7]开始向前数1个元素(只有a[7]),即c[7]; 

然后将这个1舍掉,得到6,二进制表示为0110,右边第一个1出现在第1位上,也就是说要从a[6]开始向前数2个元素(a[6],a[5]),即c[6];

然后舍掉用过的1,得到4,二进制表示为0100,右边第一个1出现在第2位上,也就是说要从a[4]开始向前数4个元素(a[4],a[3],a[2],a[1]),即c[4].

         树状数组我们可以把它理解为一种储存数据的特殊数据结构，与普通的数组相似都是用于储存数据，但与普通数组不相同的地方在于，比如我想算第1项到第7项的和，普通数组必须sum+=a[i]（sum初始化为0，1=<i<=7）,对于树状数组而言，由上面已经知道，s[7]=c[7]+c[6]+c[4]（树状数组在读入数据时和普通数组不同，需要进行下特殊的处理，也就是说此时的c[i]不等同于a[i]，后面的代码段中我会一点点说明）,这样来看的话树状数组比普通数组在某段内求和具有了更高的效率，时间也会节省很多。

 

        树状数组的模板代码实现：

       int lowbit(int x)//计算lowbit，需要特别注意下x一般不能等与0，因为 0&（-0）=0。
{
    return x&(-x);
}
void add(int i,int val)//将第i个元素的值加上val
{
    while(i<=n)
    {
        c[i]+=val;
        i+=lowbit(i);       //如果i=0,就会陷入死循环，永远无法跳出  ，lowbit(i)=0
    }
}
int sum(int i)//求前i项和
{
    int s=0;
    while(i>0)
    {
        s+=c[i];
        i-=lowbit(i);
    }
    return s;
}

       根据上面的函数模板，我具个简单的例子，加深下对树状数组的理解

     题目大意：比如说有5个兵营地，开始时给出了每个兵营地的初始值（我们就假设每个兵营地的人数为1人），接下来我们可以有下面几个操作1.向第i个（1=<i<=5，后面的i相同）兵营地中加入val个人   2.向第i个兵营地中减少val人（我们可以理解为加入-val人）   3.查询第i个营地到第j个营地的人数和（也就是POJ1166我对它题意的简化）

      首先拿到这个问题后，你可能会觉得这题直接用普通数组就能实现，但是如果我们将兵营地的数量扩充到50000，对于操作的次数我们也取一个很大的值，也就是说我们需要频繁的在一个数量个数特别大的营地里进行加入，减少，和查询的操作，而时间我们也卡得很紧，普通数组一般方法实现的话一定会超时，这时你想到了什么呢？没错，这个性质不就适合树状数组吗（当然线段树也能很好的实现，线段树的相关知识我以后再更新）。

      重新回到题目，假设我们一共接到了3条命令，<1>向第3个营地里加入2人 <2>向第5个营地里减少1人 <3>查询第1个营地到第5个营地的人数总和。

      我们用数组c[i]=1(1=<i<=5)用来存放兵营地的初始值，<1>我们直接使用 add(3,2),此时数组c更新为了c[1]=1,c[2]=1,c[3]=3,c[4]=3,c[5]=1  <2>add(5,-1) 此时数组更新为c[1]=1,c[2]=1,c[3]=3,c[4]=3,c[5]=0  <3>sum(5) 此时就得出了结果    

 

      这篇随笔就是简单的介绍下树状数组吧，后面我也会慢慢的把做过的树状数组的题目解题报告贴到博客园上