图,深度优先遍历与广度优先遍历
1.为什么要有图
1)前面学了线性表和树
2)线性表局限于一个直接前驱和直接后继的关系
3)树也只能有一个直接前驱也就是父节点
4)当我们需要表示多对多的关系时,这里就需要用到图
图也是一种数据结构,其中结点可以具有零个或多个相邻元素。两个结点之间的连接成为边。结点也可以称为顶点。
图的相关概念:
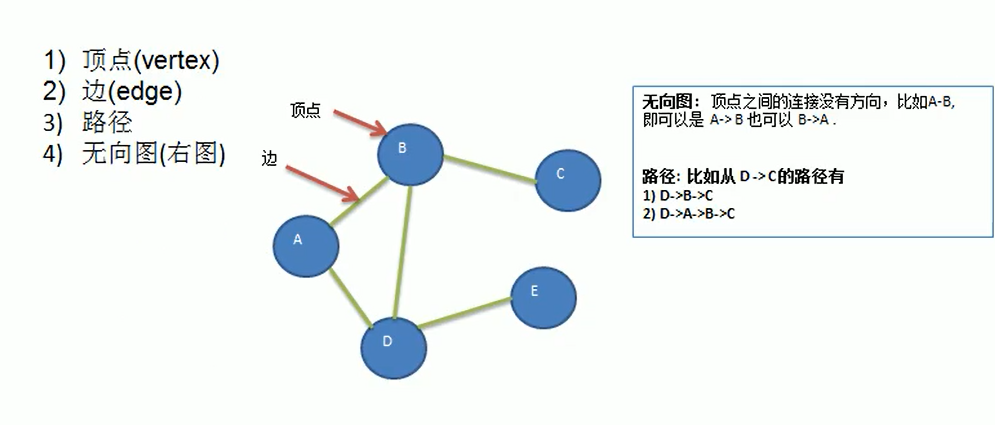

图的表示方式:
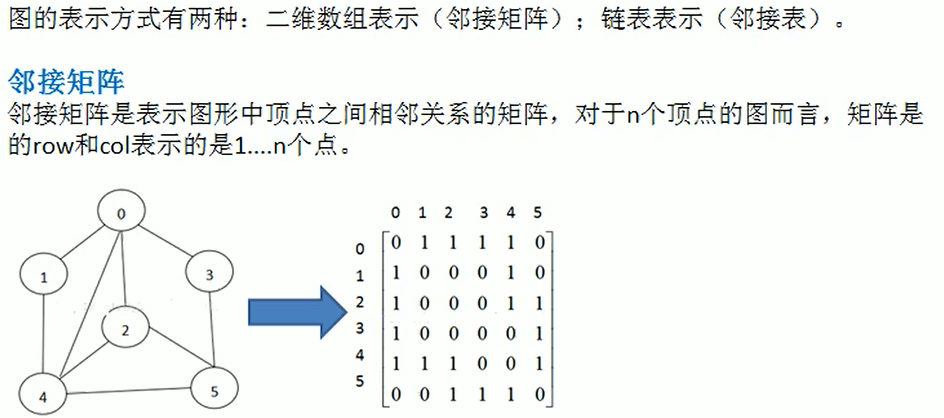
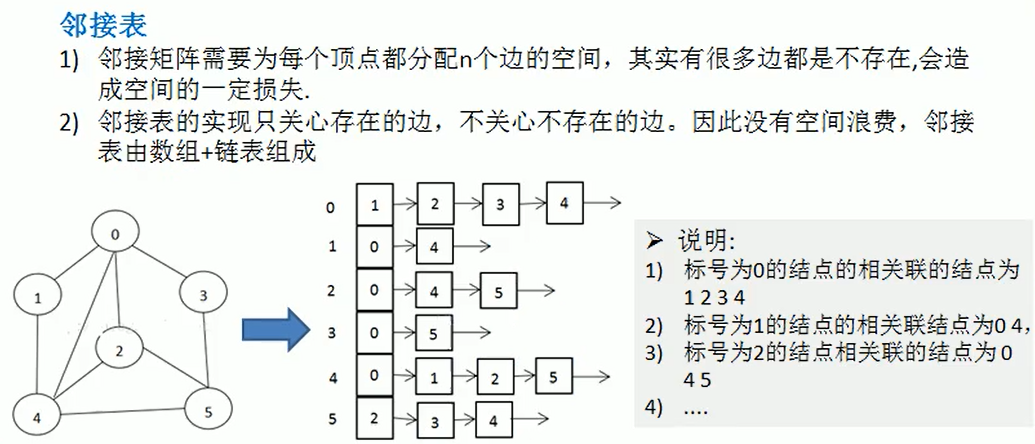
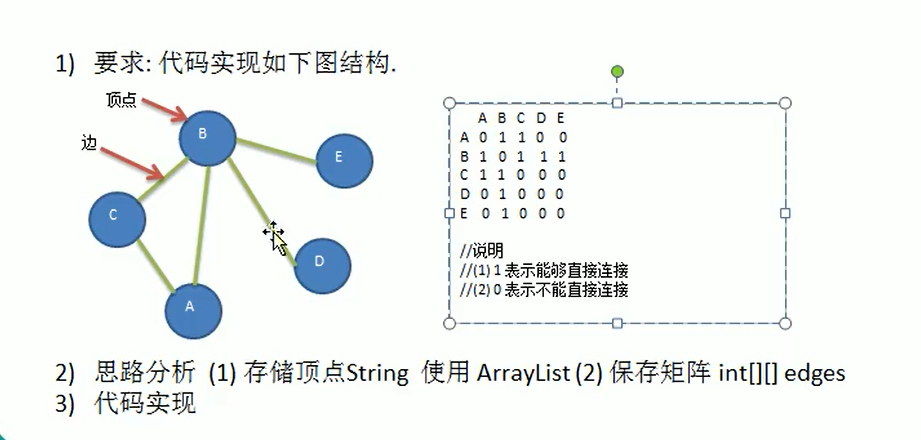
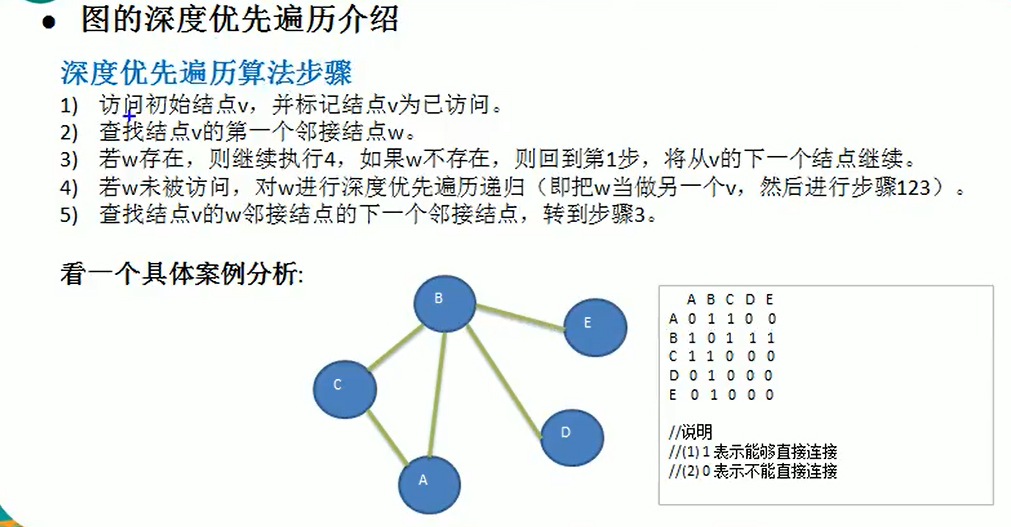
图的深度优先

图的广度优先

代码实现:
import java.util.ArrayList; import java.util.Arrays; import java.util.LinkedList; public class Graph { private ArrayList<String> vertexList; //存储顶点集合 private int[][] edges; //存储图对应的邻结矩阵 private int numOfEdges; //表示边的数目 //定义给数组boolean[], 记录某个结点是否被访问 private boolean[] isVisited; public static void main(String[] args) { //测试一把图是否创建ok int n = 8; //结点的个数 //String Vertexs[] = {"A", "B", "C", "D", "E"}; String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"}; //创建图对象 Graph graph = new Graph(n); //循环的添加顶点 for(String vertex: Vertexs) { graph.insertVertex(vertex); } //添加边 //A-B A-C B-C B-D B-E // graph.insertEdge(0, 1, 1); // A-B // graph.insertEdge(0, 2, 1); // // graph.insertEdge(1, 2, 1); // // graph.insertEdge(1, 3, 1); // // graph.insertEdge(1, 4, 1); // //更新边的关系 graph.insertEdge(0, 1, 1); graph.insertEdge(0, 2, 1); graph.insertEdge(1, 3, 1); graph.insertEdge(1, 4, 1); graph.insertEdge(3, 7, 1); graph.insertEdge(4, 7, 1); graph.insertEdge(2, 5, 1); graph.insertEdge(2, 6, 1); graph.insertEdge(5, 6, 1); //显示一把邻结矩阵 graph.showGraph(); //测试一把,我们的dfs遍历是否ok System.out.println("深度遍历"); graph.dfs(); // A->B->C->D->E [1->2->4->8->5->3->6->7] // System.out.println(); System.out.println("广度优先!"); graph.bfs(); // A->B->C->D-E [1->2->3->4->5->6->7->8] } //构造器 public Graph(int n) { //初始化矩阵和vertexList edges = new int[n][n]; vertexList = new ArrayList<String>(n); numOfEdges = 0; } //得到第一个邻接结点的下标 w /** * * @param index * @return 如果存在就返回对应的下标,否则返回-1 */ public int getFirstNeighbor(int index) { for(int j = 0; j < vertexList.size(); j++) { if(edges[index][j] > 0) { return j; } } return -1; } //根据前一个邻接结点的下标来获取下一个邻接结点 public int getNextNeighbor(int v1, int v2) { for(int j = v2 + 1; j < vertexList.size(); j++) { if(edges[v1][j] > 0) { return j; } } return -1; } //深度优先遍历算法 //i 第一次就是 0 private void dfs(boolean[] isVisited, int i) { //首先我们访问该结点,输出 System.out.print(getValueByIndex(i) + "->"); //将结点设置为已经访问 isVisited[i] = true; //查找结点i的第一个邻接结点w int w = getFirstNeighbor(i); while(w != -1) {//说明有 if(!isVisited[w]) { dfs(isVisited, w); } //如果w结点已经被访问过 w = getNextNeighbor(i, w); } } //对dfs 进行一个重载, 遍历我们所有的结点,并进行 dfs public void dfs() { isVisited = new boolean[vertexList.size()]; //遍历所有的结点,进行dfs[回溯] for(int i = 0; i < getNumOfVertex(); i++) { if(!isVisited[i]) { dfs(isVisited, i); } } } //对一个结点进行广度优先遍历的方法 private void bfs(boolean[] isVisited, int i) { int u ; // 表示队列的头结点对应下标 int w ; // 邻接结点w //队列,记录结点访问的顺序 LinkedList queue = new LinkedList(); //访问结点,输出结点信息 System.out.print(getValueByIndex(i) + "=>"); //标记为已访问 isVisited[i] = true; //将结点加入队列 queue.addLast(i); while( !queue.isEmpty()) { //取出队列的头结点下标 u = (Integer)queue.removeFirst(); //得到第一个邻接结点的下标 w w = getFirstNeighbor(u); while(w != -1) {//找到 //是否访问过 if(!isVisited[w]) { System.out.print(getValueByIndex(w) + "=>"); //标记已经访问 isVisited[w] = true; //入队 queue.addLast(w); } //以u为前驱点,找w后面的下一个邻结点 w = getNextNeighbor(u, w); //体现出我们的广度优先 } } } //遍历所有的结点,都进行广度优先搜索 public void bfs() { isVisited = new boolean[vertexList.size()]; for(int i = 0; i < getNumOfVertex(); i++) { if(!isVisited[i]) { bfs(isVisited, i); } } } //图中常用的方法 //返回结点的个数 public int getNumOfVertex() { return vertexList.size(); } //显示图对应的矩阵 public void showGraph() { for(int[] link : edges) { System.err.println(Arrays.toString(link)); } } //得到边的数目 public int getNumOfEdges() { return numOfEdges; } //返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C" public String getValueByIndex(int i) { return vertexList.get(i); } //返回v1和v2的权值 public int getWeight(int v1, int v2) { return edges[v1][v2]; } //插入结点 public void insertVertex(String vertex) { vertexList.add(vertex); } //添加边 /** * * @param v1 表示点的下标即使第几个顶点 "A"-"B" "A"->0 "B"->1 * @param v2 第二个顶点对应的下标 * @param weight 表示 */ public void insertEdge(int v1, int v2, int weight) { edges[v1][v2] = weight; edges[v2][v1] = weight; numOfEdges++; } }


