二叉树、平衡二叉树、红黑树、B树、B+树

二叉树

特点

二叉树特点是，根节点有俩孩子，左小右大（左<根/中<右）
查找比线性链表或数组快

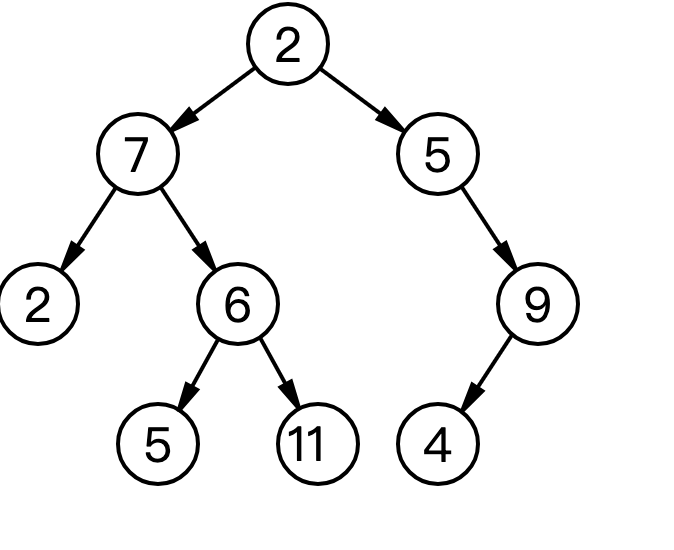
极端情况变链表

但是有一种极端情况，会退化成一个链表：数据从小到大或从大到小，比如：
1 2 3 4 5 6 7 放入二叉树

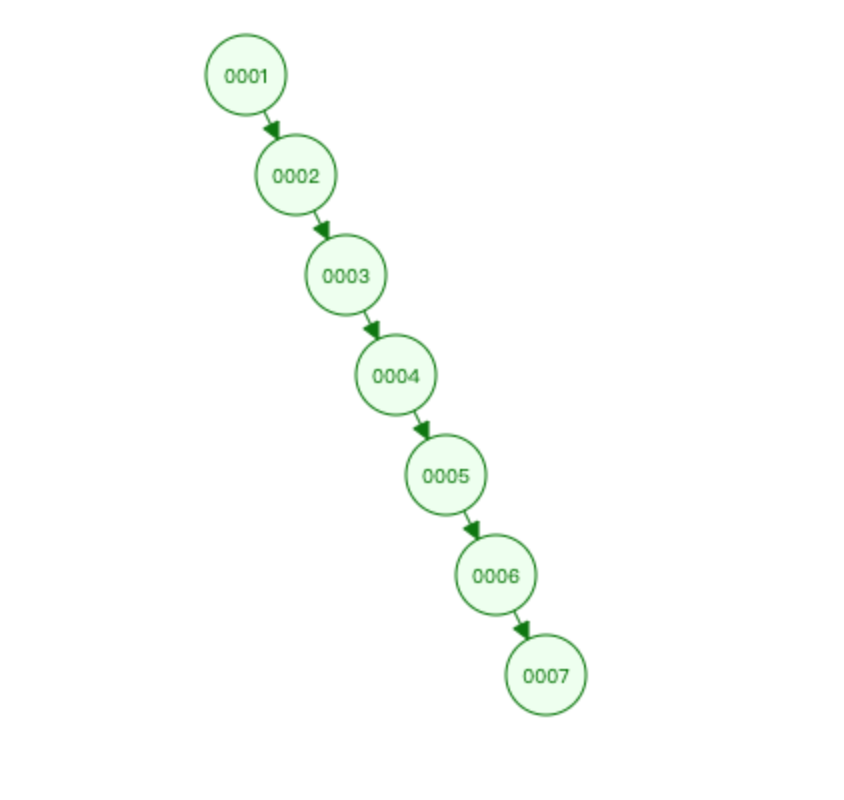
二叉树的遍历

组装一棵二叉树如下：

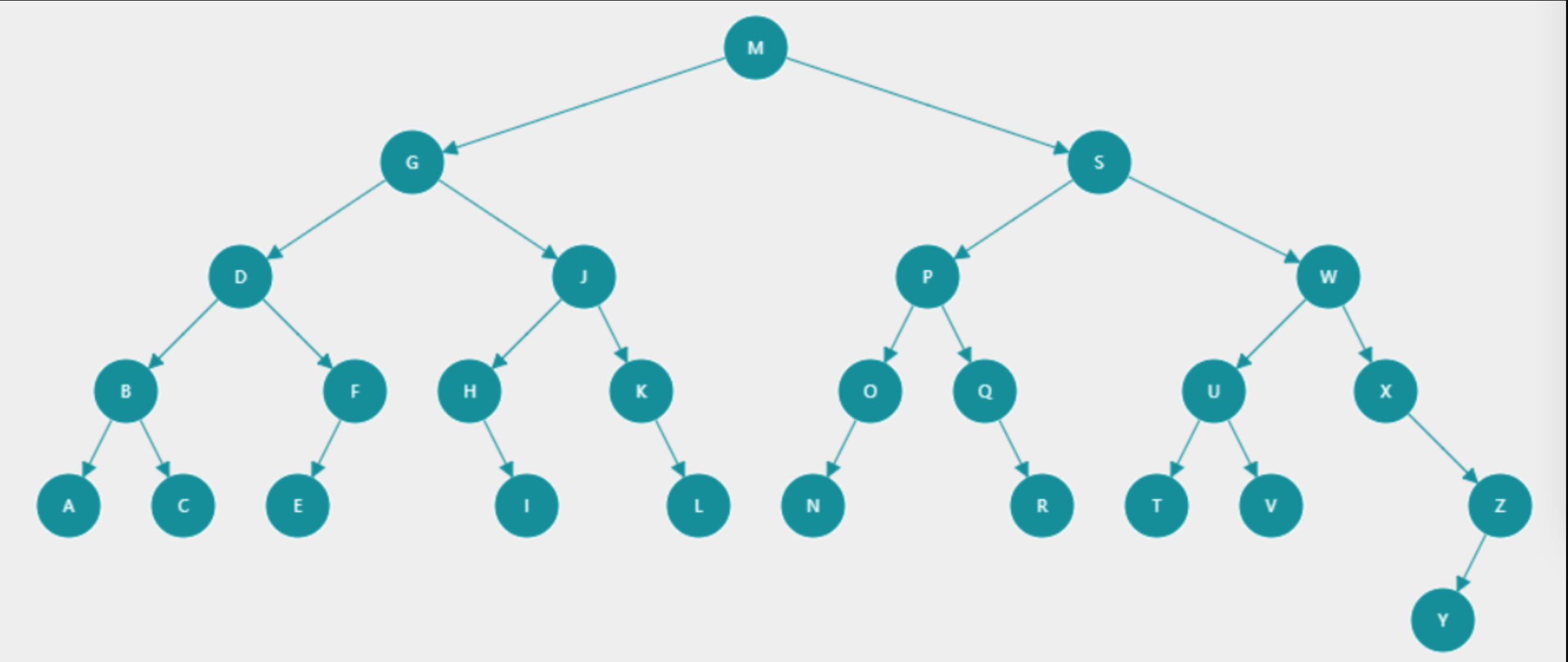
• 前序遍历（中->左子->右子，根节点M在前面）
  
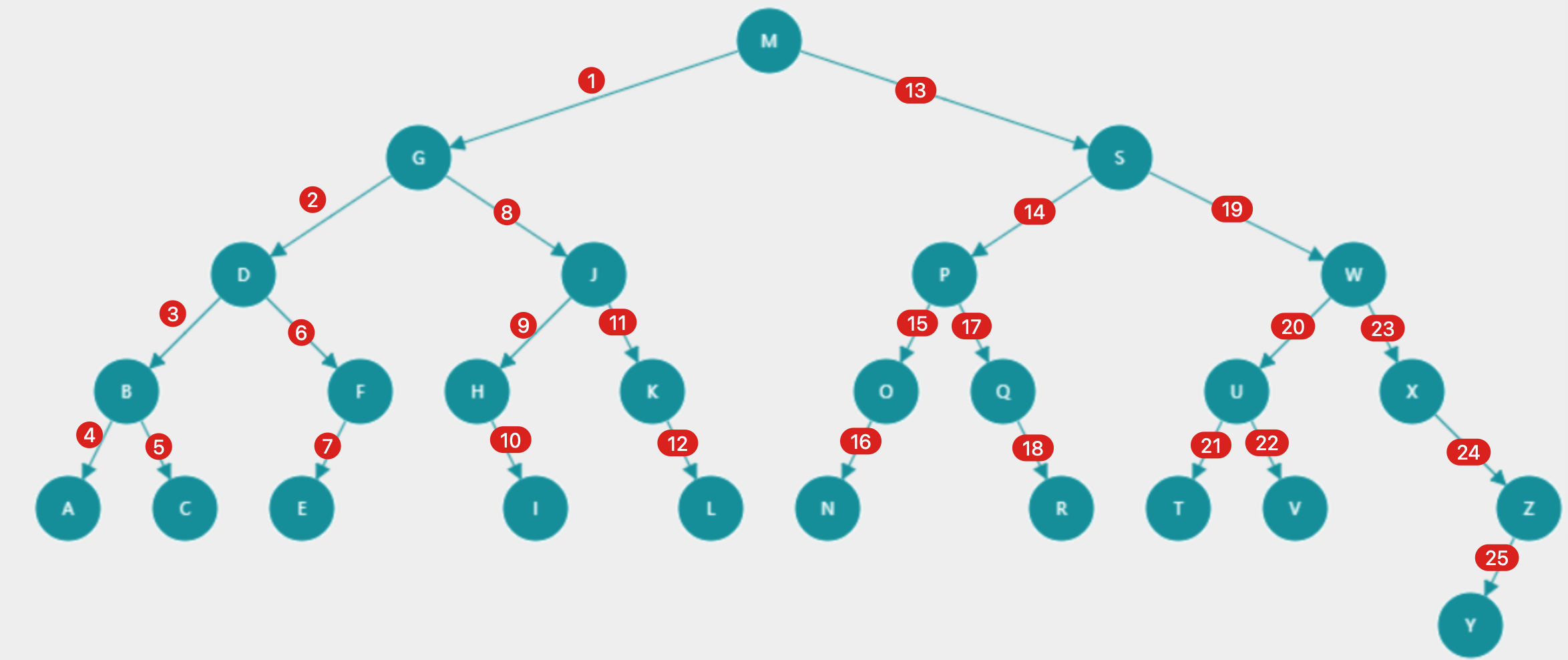
  结果：
  M，G，D，B，A，C，F，E，J，H，I，K，L，S，P，O，N，Q，R，W，U，T，V，X，Z，Y
• 后续遍历（左子->右子->中，根节点M在最后）
  
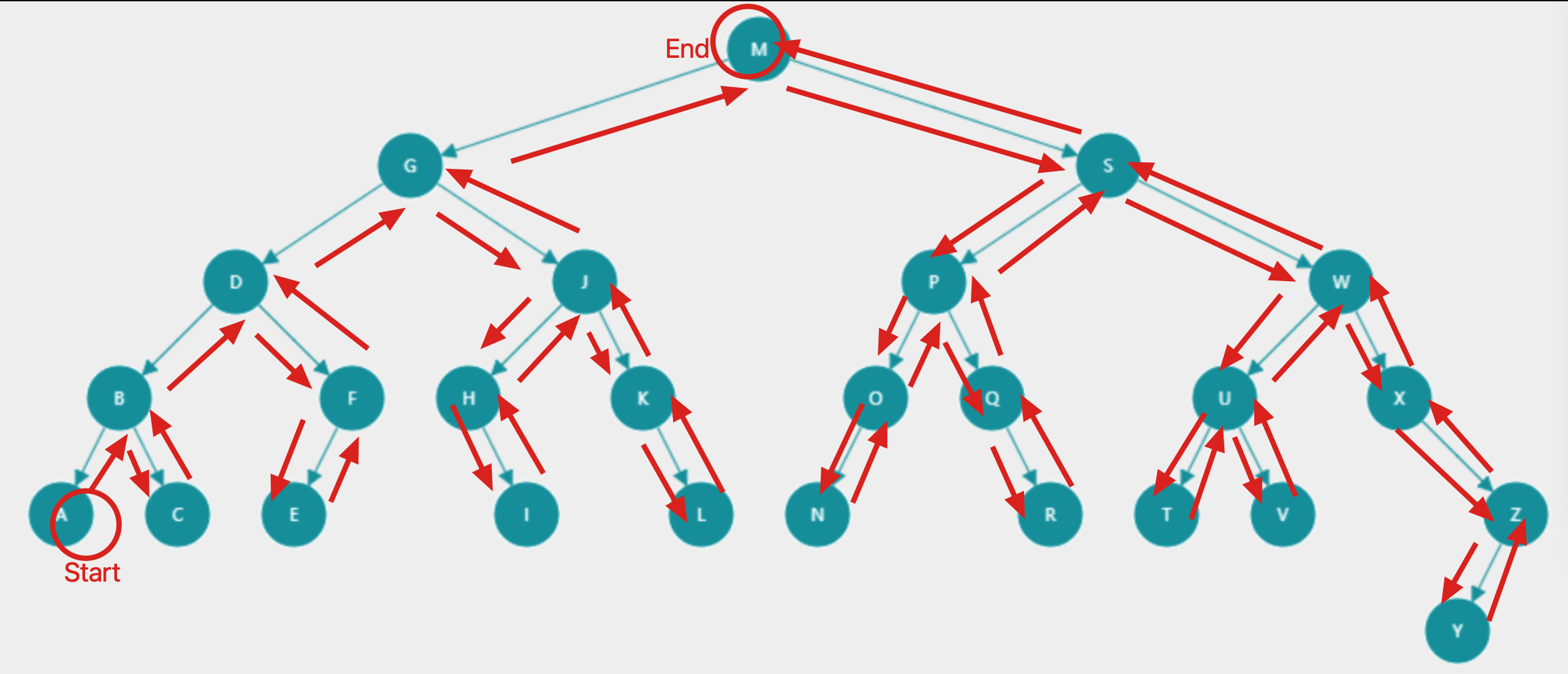
  结果：
  A，C，B，E，F，D，I，H，L，K，J，G，N，O，R，Q，P，T，V，U，Y，Z，X，W，S，M
• 中序遍历（左子->中->右子，根节点M在中间）
  结果：
  A，B，C，D，E，F，G，H，I，J，K，L，M，N，O，P，Q，R，S，T，U，V，W，X，Y，Z

平衡二叉树

为了避免出现链表或者子节点数据量不一致问题，又出现了平衡（AVL）二叉树。
平衡二叉树，当左右子节点树高差大于1时，通过左旋或右旋来保持整颗树的平衡
比如 1 2 3 4 5 6 7 放入平衡二叉树

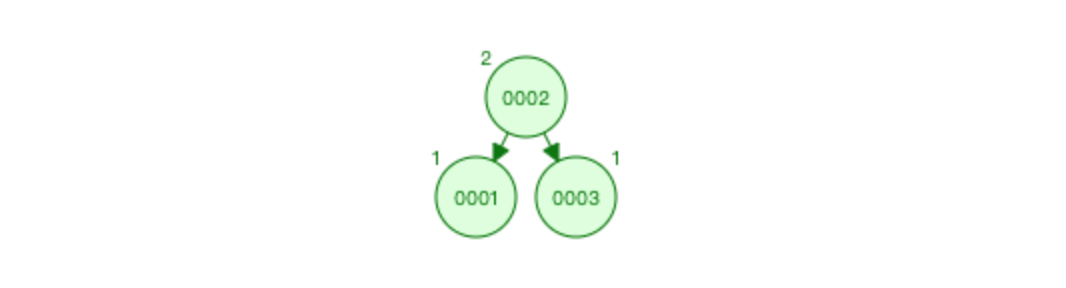
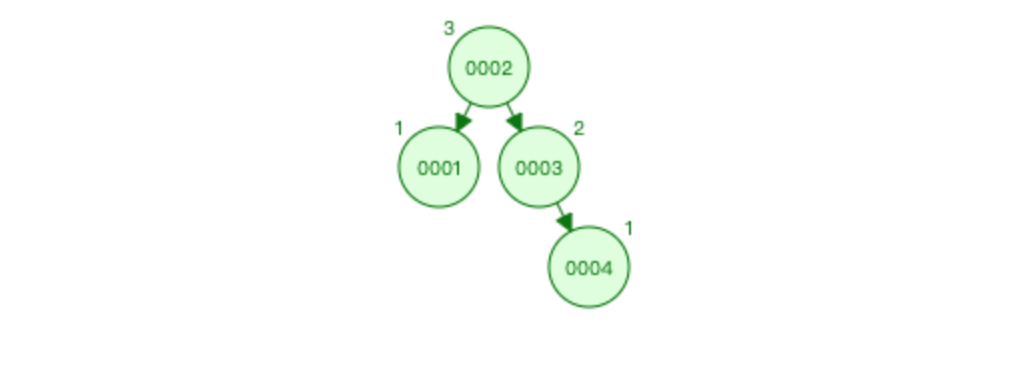
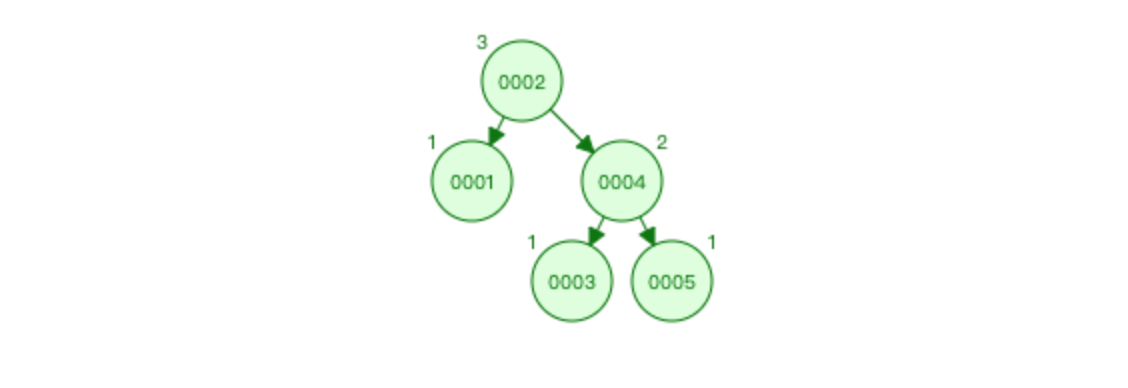
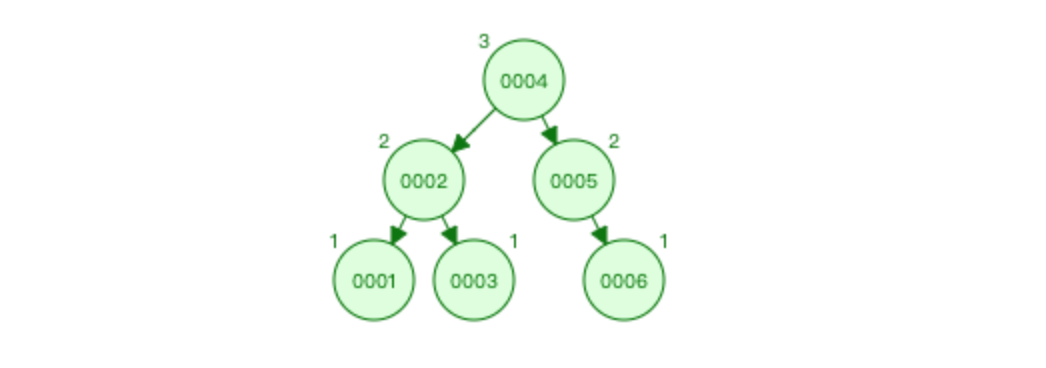
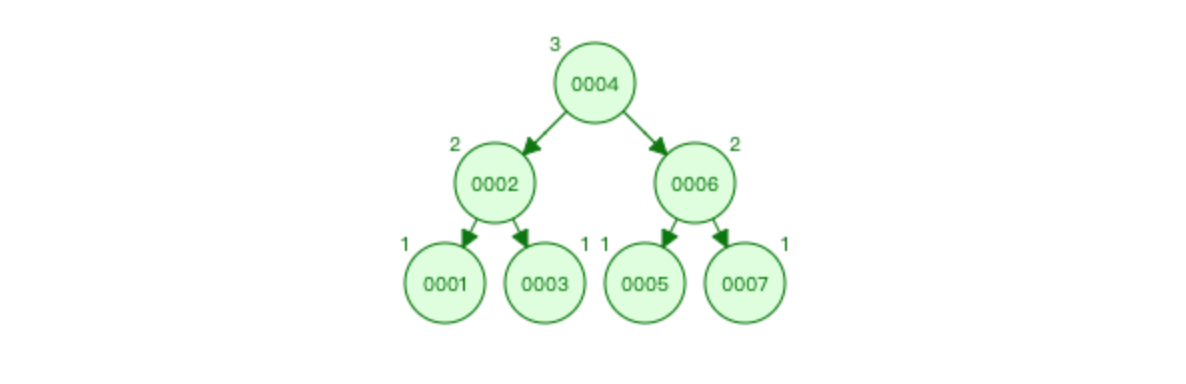
特点：

• 非叶子节点最多拥有两个子节点
• 非叶子节点值大于左边子节点、小于右边子节点
• 树的左右两边的层级数相差不会大于1
• 没有值相等重复的节点

红黑树

因为平衡二叉树每次加入数据，为了保持整棵树的平衡，要做大量的节点旋转移动，所以又出现了红黑树

与AVL树相比，红黑树牺牲了部分平衡性，以换取插入/删除操作时较少的旋转操作（这也是为什么 Java 的 HashMap 和多路复用技术 Epoll 使用红黑树而不是平衡二叉树的原因）

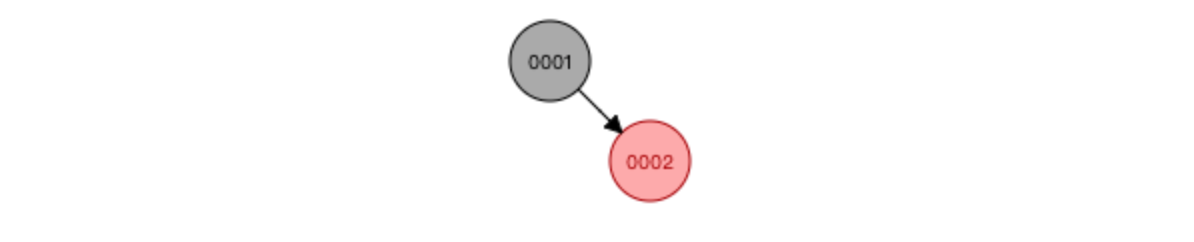
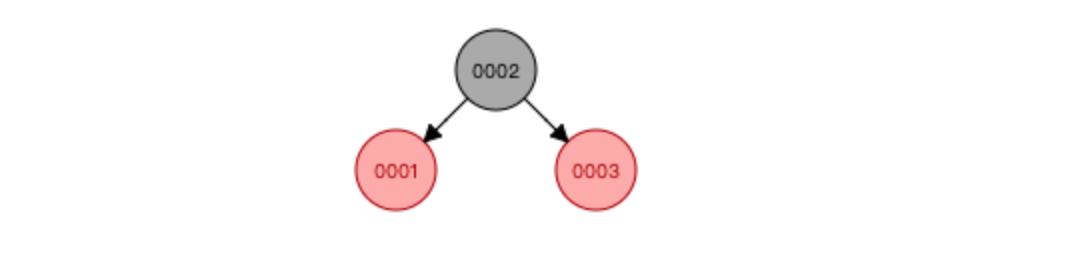
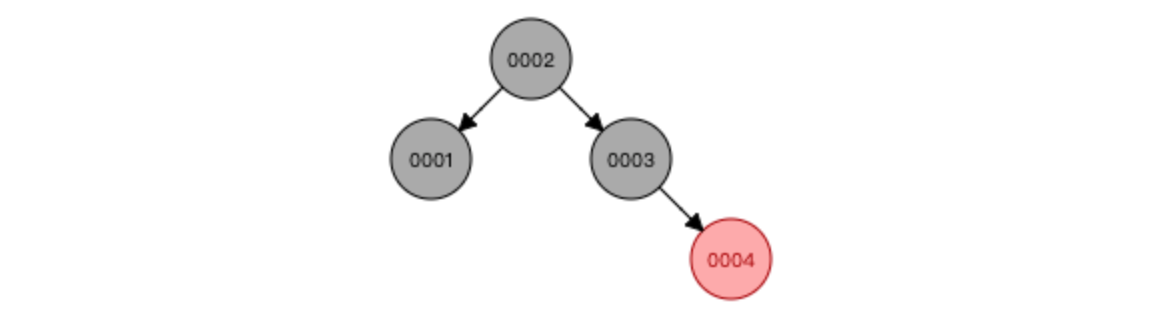
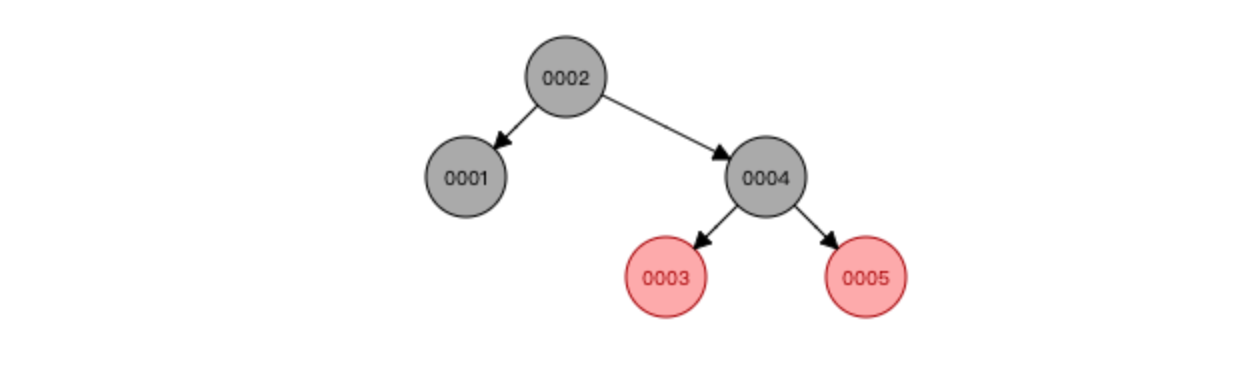
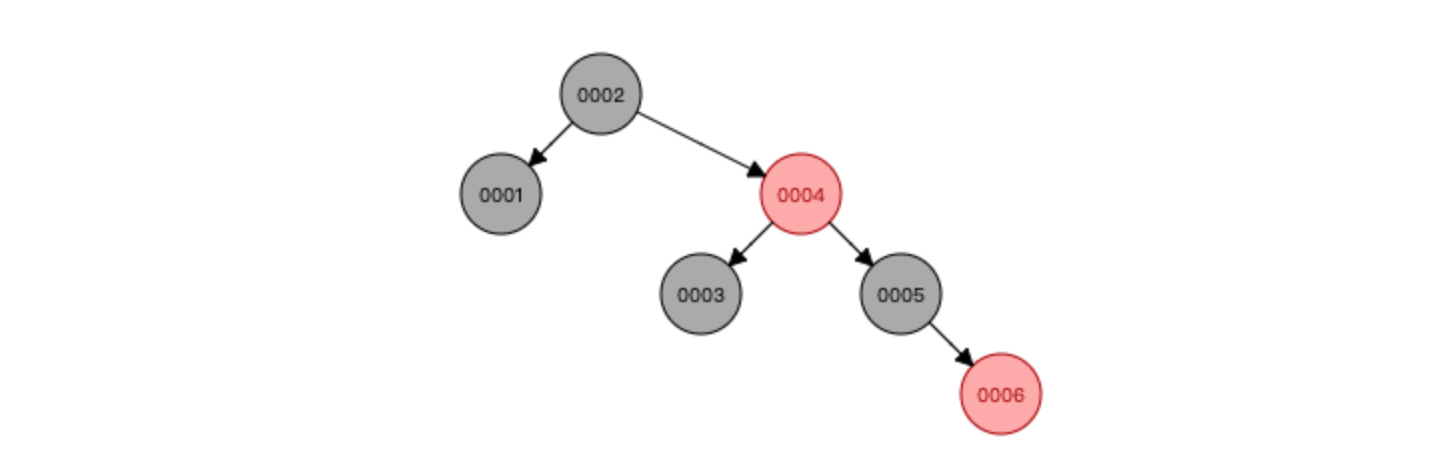
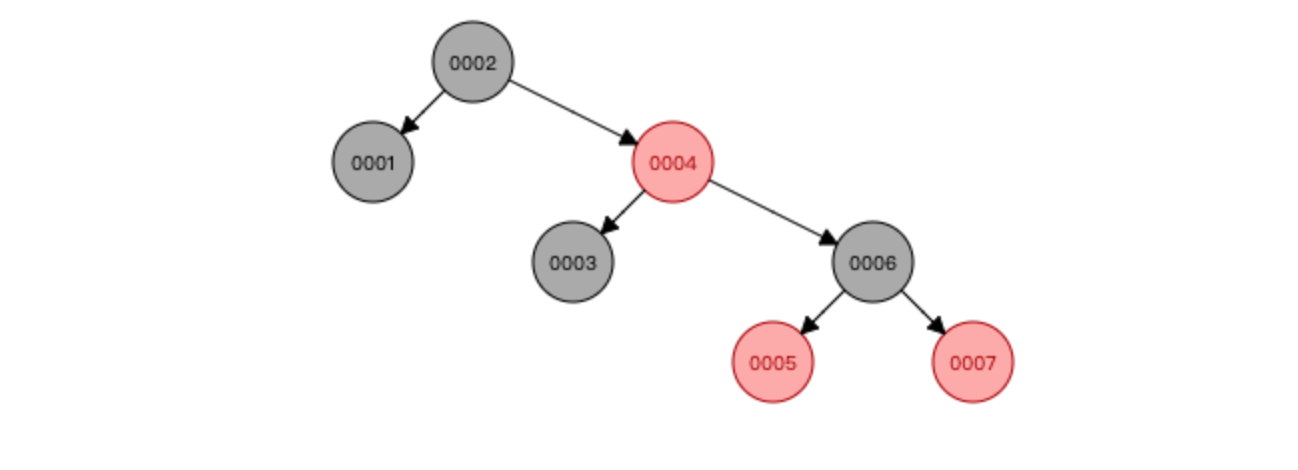
红黑树特点

• 每个节点是黑色或者红色
• 根节点一定是黑色
• 每个叶子节点(NIL)是黑色
• 如果一个节点是红色的，则它的子节点必须是黑色的
• 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点

通俗理解：黑色可以理解为平衡特征，如果满足不了平衡特征，就要进行平衡操作

B树

B树，实际上是多路平衡树，相比二叉树，B树可以存储更多信息和数据

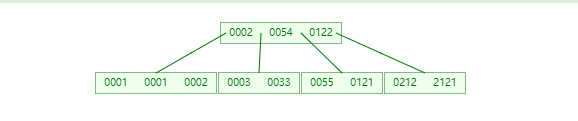
概念：

• M阶：表示有M路查找路径。M=2时就是二叉树，M=3就是三叉树
• 关键字数：节点的关键字数量 >=ceil(m/2)-1 且 <= M-1
• ceil 函数：ceil()是个朝正无穷方向取整的函数。 如 ceil(1.1) = 2

比如下图，M=5，表示为5阶树。当节点中数据大于等于5，就会向下拆分

|
V

B+树

B+树是在B树的基础上又做了改进：

• 查询稳定性
• 数据排序
• B+树的非叶子节点不保存具体的数据，而只保存关键字的索引，而所有的数据最终都会保存到叶子节点

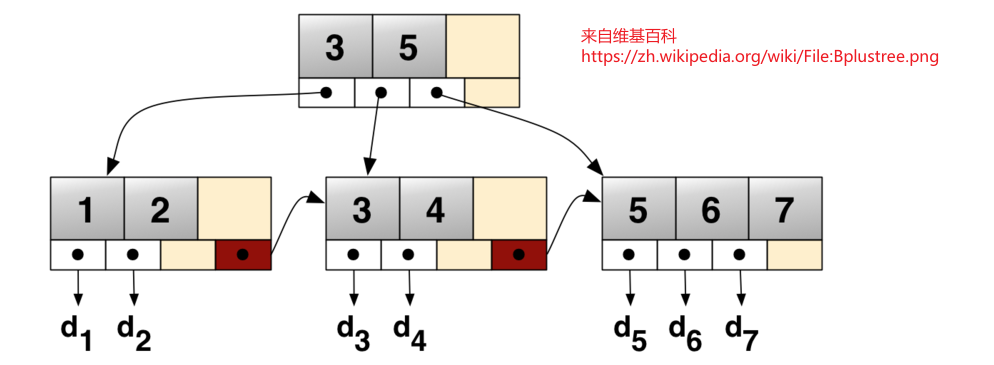
• 所有关键字都出现在叶子节点的链表中（稠密索引），且关键字是有序的
• 不会在非叶子节点命中查询
• 非叶子节点是叶子节点的索引（稀疏索引），叶子节点相当于是存储（关键字）数据的数据层
  

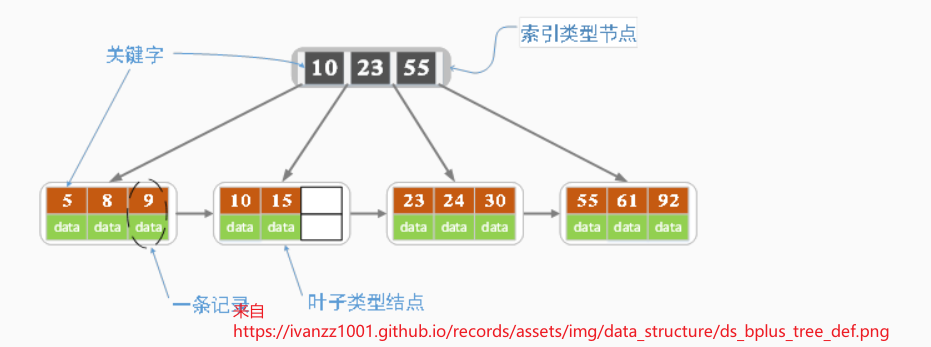
MySQL 使用 B+树的好处

• B-树和B+树最重要的一个区别就是B+树只有叶子节点存放数据，其余节点用来索引。而B-树是每个索引节点都会存数据。所以B+树更适合用来存储磁盘数据
• B+树是用来做索引的，数据量非常大，索引也会存储在磁盘上
• B+树的关键信息存储量更多，B+树的非叶子节点不存储数据，只存储关键字和指针，关键信息存储量比B树更多，磁盘IO更少
• B+树的查询效率更加稳定。B+树任何关键字的查找从根节点到叶子节点的查询路径长度相同，每个数据的查询效率相当
• B+树更适合范围（区间）查询，所有的叶子节点用指针按顺序串起来，这样遍历叶子节点就能获得全部数据并且是有序的，更加适合范围查询