【算法】K-means 算法学习

K-means算法是一种非监督学习的聚类算法，它通过计算样本点之间的距离来将数据点划分为多个聚类。

K-means算法的核心思想是，通过预先设定的K值及每个类别的初始质心，对相似的数据点进行划分。然后，通过迭代优化，不断调整聚类中心，直到聚类中心不再发生变化或者达到预设的迭代次数。

在K-means算法中，每个聚类的中心点被称为质心，而每个数据点被分配到最近的质心所在的聚类中。算法的目标是使每个聚类的内部距离最小，同时使聚类之间的距离最大。

需要注意的是，K-means算法对初始质心的选择比较敏感，不同的初始质心可能会导致不同的聚类结果。此外，K-means算法还可能受到异常值的影响，因为异常值可能会对质心的计算产生较大的影响。

K-means算法的缺点主要是：

• 需要人工选择K值，未必符合真实数据分布（可以通过尝试“手肘法”找到合适的K值，也就是将函数不同K值的曲线画出来找到拐点对应的K值）
• 受初始中心和离散点的影响较为严重，稳定性较差
• 通常结果并非全局最优，而是局部最优

K-means算法的优点主要是：

• 对于大数据，算法复杂度为线性：O(NKT) (N样本个数，K聚类中心个数，T迭代轮数)
• 局部最优解通常已经满足问题的需要

K-means算法改进：

• 选择最初的聚类中心时，要保证相互之间的距离尽可能远

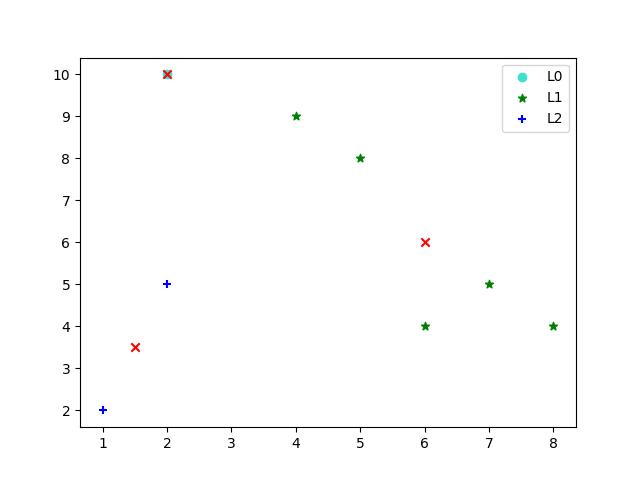
from numpy import *
import pandas as pd
import matplotlib.pyplot as plt
 
# 计算两点之间的欧式距离
def dist(a, b):
    return sqrt(sum((a - b) ** 2))
 
# 生成聚类中心
def create_center(data, k, defaultPts=[0,3,6]):
    pt = zeros((k, n), dtype=float64)
    set = []
    for i in range(k):
        dpt = None if defaultPts is None else defaultPts[i]
        if dpt is None:
            # 如果没有默认点，则随机选取一个点作为聚类中心
            dpt = random.randint(0, len(data) - 1)
            while (dpt in set):
                # 如果随机选取的点已经存在，则重新随机选取一个点作为聚类中心
                dpt = random.randint(0, len(data) - 1)
        set.append(dpt)
        pt[i] = data[dpt]
    return pt
 
# 聚类
def kMeans(data, k, dist, centroids):
    # 样本个数
    m = shape(data)[0]
    print(centroids)
 
    # 聚类结果
    init = zeros((m, 2), dtype=float64)
    # 存储中间结果的矩阵
    cluster_assment = mat(init)
 
    for epoch in range(500):
        for i in range(m):
            # 计算每个样本到最近的聚类中心的距离
            min_dist = inf
            for j in range(k):
                # 计算样本到聚类中心的距离
                dist_ij = dist(data[i], centroids[j])
                # 找到最近的聚类中心
                if dist_ij < min_dist:
                    min_dist = dist_ij
                    # 更新样本所属的聚类中心，第1列为聚类中心的序号，第2列为距离
                    cluster_assment[i] = j, min_dist
 
        # 对所有节点聚类之后，重新更新中心
        changeRef = 0
        for j in range(k):
            pts_in_cluster = data[nonzero(cluster_assment[:, 0].A == j)[0]]
            new_centroids = mean(pts_in_cluster, axis=0)
            if new_centroids.tolist() != centroids[j].tolist():
                changeRef = changeRef + 1
                centroids[j] = new_centroids
 
        if changeRef == 0:
            print("epoch", epoch)
            break
 
    # 返回聚类中心和聚类结果
    return centroids, cluster_assment
 
 
if __name__ == '__main__':
    # 数据集
    data = array([[2, 10], [2,5], [8, 4], [5, 8], [7, 5], [6, 4], [1, 2], [4, 9]])
 
    # 聚类个数
    k = 3
    # 特征个数
    n = 2
 
    # 聚类
    centroids, cluster_assment = kMeans(data, k, dist=dist, centroids=create_center(data, k, None))
 
    # 聚类结果
    predict_label = cluster_assment[:, 0]
    # 给样本增加一列，表示样本所属的聚类结果
    data_and_pred = column_stack((data, predict_label))
 
    # 原始的数据样本和预测出来的类别
    df = pd.DataFrame(data_and_pred, columns=['x1', 'x2', 'label'])
    df0 = df[df['label'] == 0].values
    df1 = df[df['label'] == 1].values
    df2 = df[df['label'] == 2].values
 
    # 画图
    plt.scatter(df0[:, 0], df0[:, 1], c='turquoise', marker='o', label='L0')
    plt.scatter(df1[:, 0], df1[:, 1], c='g', marker='*', label='L1')
    plt.scatter(df2[:, 0], df2[:, 1], c='b', marker='+', label='L2')
    plt.scatter(centroids[:, 0].tolist(), centroids[:, 1].tolist(), c='r', marker='x')
    # 图例位置
    plt.legend(loc=1)
    # 显示图
    plt.show()