算法-搜索（6）B树

B树是平衡的m路搜索树。

根结点至少两个子女，根结点以外的非失败结点至少⌈m/2⌉个子女，所有失败结点都在h+1层。

第h层至少2⌈m/2⌉^h-1个结点，因此失败结点数n+1≥2⌈m/2⌉^h-1个。

每个结点包含一组指针recptr[m]，指向实际记录的存放地址。recptr[i]与key[i]形成了一个索引项

注：key[0]~key[n]和ptr[0]~ptr[n]（n<m）

1.B树的插入

每个非失败结点都有⌈m/2⌉-1~m-1个关键码，插入后超过范围的话需要分裂结点。

前⌈m/2⌉-1个关键码形成结点p，后m-⌈m/2⌉个结点形成结点q，第⌈m/2⌉个关键码和指向q的指针插入到p的父结点。

最差情况下，自顶向下搜索叶结点需要h次读盘，自底向上分裂路径上每一个结点。分裂非根结点时插入两个结点，分裂根结点时插入三个结点。需要读写磁盘次数=3h+1（不考虑读入的结点再向上插入时需要重新从磁盘读入）

当m较大时，访问磁盘的平均次数接近h+1。

2.B树的删除

如果被删关键码不在叶结点，在删去后就找其后一个指针指向的子树里最小的关键码x替代，再删去叶结点的关键码x。

在叶结点中删去关键码：

（1）被删关键码所在结点是根结点、结点关键码个数n≥2，直接删除关键码并将结点写回磁盘。

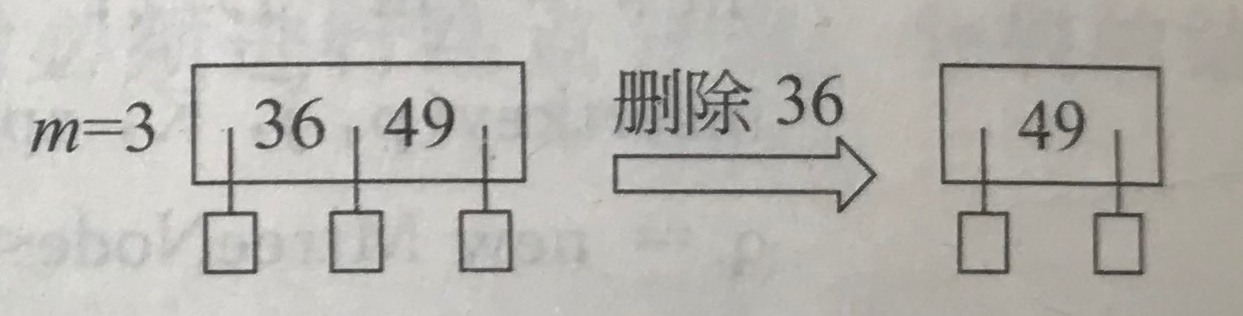
（2）被删关键码所在结点不是根结点、结点关键码个数n≥⌈m/2⌉，，直接删除关键码并将结点写回磁盘。

 

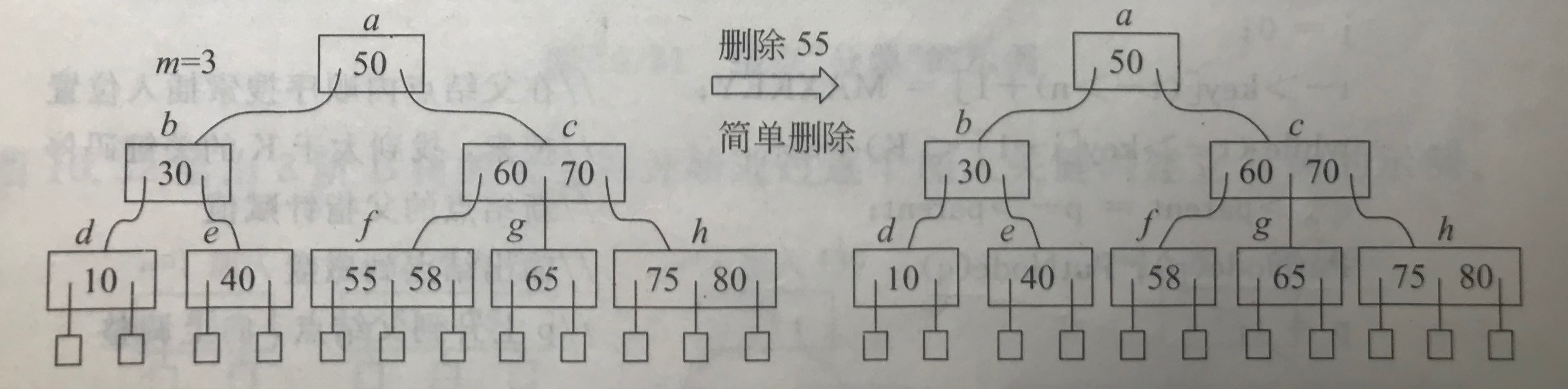
（3）被删关键码在叶结点、结点关键码个数n=⌈m/2⌉-1、相邻右兄弟/左兄弟结点关键码个数n≥⌈m/2⌉

①将父结点刚刚好大于/小于待删关键码的关键码下移到待删关键码的位置。

②将右兄弟/左兄弟结点中的最小/最大关键码上移到父结点的该位置。

③将右兄弟/左兄弟结点的最左/右子树指针平移到被删关键码所在结点的最后/最前子树指针位置。

④右/左兄弟结点被移走了一个关键码和一个指针，需要要剩下的填补调整，结点的关键码个数n也要减1。

 

（4）被删关键码在叶结点、结点关键码个数n=⌈m/2⌉-1、相邻右兄弟/左兄弟结点关键码个数n=⌈m/2⌉-1，则需要合并结点。

①将父结点p刚刚好大于待删关键码的关键码下移到待删关键码的位置。

②将若要合并p中子树指针p_i和所p_i+1指向的结点，并保留p_i指向的结点，则将K_i+1关键码下移。

③把要指向p_i结点全部关键码和指针都移到p_i+1指向结点，并将其删除。

④p结点被移走了一个关键码和一个指针，需要要剩下的填补调整，结点的关键码个数n也要减1。

⑤如果p结点是根结点且关键码个数减少到了0，则将其删去，合并后结点作为新根；如果p结点不是根结点且关键码个数减少到了⌈m/2⌉-1，它要和自己的兄弟结点合并并重复该过程；

 

template <class T>
class Btree:public Mtree<T>{    //B树类继承自m树
public:
    Btree();
    bool Insert(const T& x);
    bool Remove(T& x);
    void LeftAdjust(MtreeNode<T> *p,MtreeNode<T> *q,int d,int j);
    void RightAdjust(MtreeNode<T> *p,MtreeNode<T> *q,int d,int j);
    void compress(MtreeNode<T> *p,int j);
    void merge(MtreeNode<T> *p,MtreeNode<T>* q,MtreeNode<T> *pl,int j);
};

template <class T>
bool Btree<T>::Insert(const T& x){
    //将关键码x插入到一个驻留在磁盘的m阶B树中
    Triple<T> loc=Search(x);
    if(!loc.tag) return false;  //已存在
    MtreeNode<T> *p=loc.r,*q;   //p是关键码要插入的结点地址
    MtreeNode<T> *ap=NULL,*t;   //ap是插入码x的右邻指针
    T k=x;int j=loc.i;   //（k,ap）形成插入二元组
    while(1){
        if(p->n<m-1){    //结点关键码个数未超出
            insertkey(p,j,k,ap);
            PutNode(p);
            return true;
        }
        int s=(m+1)/2;  //准备分裂结点
        insertkey(p,j,k,ap);   //插入后p->n达到m
        q=new MtreeNode<T>;
        move(p,q,s,m);  //将p的key[s+1..m]和ptr[s..m]移动到q的key[1..s-1]和ptr[0..s-1]，p->n改为s-1，q->n改为m-s
        k=p->key[s]; ap=q;  //(k,ap)形成向上插入二元组
        if(p->parent!=NULL){
            t=p->parent;GetNode(t);
            j=0;
            t->key[(t->n)+1]=MAXKEY;
            while(t->key[j+1]<k) j++;  //搜索，找到大于K的关键码停止
            q->parent=p->parent;
            PutNode(p);PutNode(q);
            p=t;   //p上升到父结点，继续调整
        }
        else{      //原p为根，需要产生新根
            root=new MtreeNode<T>;
            root->n=1;root->parent=NULL;
            root->key[1]=k;
            root->ptr[0]=p;
            root->ptr[1]=ap;
            q->parent=p->parent=root;
            PutNode(p);PutNode(q);PutNode(root);
            return true;
        }
    }
}

template <class T>
bool Btree<T>::Remove(const T& x){
    Triple<T> loc=Search(x);
    if(loc.tag) return false;  //未找到
    MtreeNode<T> *p=loc.r,*q,*s;
    int j=loc.i;       //p->key[j]==x
    if(p->ptr[j]!=NULL){   //非叶结点
        s=p->ptr[j];GetNode(s);q=p;
        while(s!=NULL){
            q=s;
            s=s->ptr[0];
        }
        p->key[j]=q->key[1];
        compress(q,1);   //把结点q中1以后的指针和关键码前移，删除key[1]
        p=q;
    }
    else compress(p,j);  //叶结点，直接删除
    int d=(m+1)/2;
    while(1){
        if(p->n<d-1){    //小于最小限制
            j=0;q=p->parent;
            GetNode(q);
            while(j<=q->n && q->ptr[j]!=p)
                j++;
            if(!j) LeftAdjust(p,q,d,j);
            else RightAdjust(p,q,d,j);
            p=q;
            if(p==root) break;
        }
        else break;
    }
    if(root->n==0){
        p=root->ptr[0];
        delete root;
        root=p;
        root->parent=NULL;
    }
    return true;
}

template <class T>
void LeftAdjust(MtreeNode<T> *p,MtreeNode<T> *q,int d,int j){
    MtreeNode<T> *pl=q->ptr[j+1];
    if(pl->n>d-1){    //右兄弟空间还够，仅做调整
        p->n++;
        p->key[p->n]=q->key[j+1];
        q->key[j+1]=pl->key[1];
        p->ptr[p->n]=pl->ptr[0];
        pl->ptr[0]=pl->ptr[1];
        compress(pl,1);
    }
    else merge(p,q,pl,j+1);  //p与pl合并，保留p结点
}

template <class T>
void RightAdjust(MtreeNode<T> *p,MtreeNode<T> *q,int d,int j){
    
}

void compress(MtreeNode<T> *p,int j){
    for(int i=j; i<p-n; i++){  //左移
        p->key[i]=p->key[i+1];
        p->ptr[i]=p->ptr[i+1];
    }
    p->n--;  //结点中元素个数减1
}
void merge(MtreeNode<T> *p,MtreeNode<T>* q,MtreeNode<T> *pl,int j){
    p->key[(p->n)+1]=q->key[j];
    p->ptr[(p->n)+1]=pl->ptr[0];
    for(int i=1; i<=pl->n; i++){
        p->key[(p->n)+i+1]=pl->key[i];
        p->ptr[(p->n)+i+1]=pl->ptr[i];
    }
    compress(q,j);
    p->n=p->n+pl->n+1;
    delete pl;
}