图

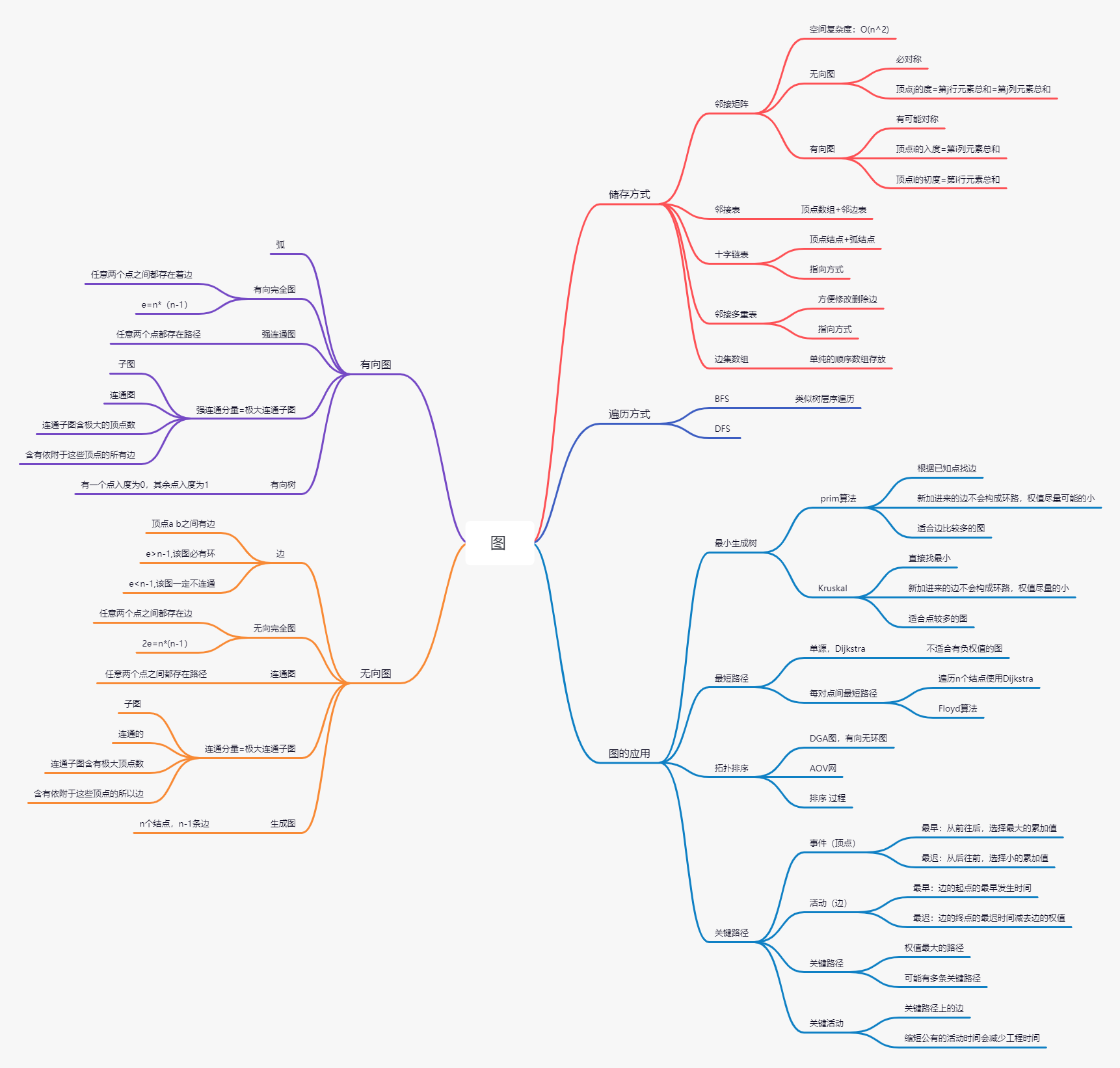
思维导图

　图的定义
图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
在图中需要注意的是：
　　（1）线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图中数据元素，我们则称之为顶点（Vertex）。
　　（2）线性表可以没有元素，称为空表；树中可以没有节点，称为空树；但是，在图中不允许没有顶点（有穷非空性）。
　　（3）线性表中的各元素是线性关系，树中的各元素是层次关系，而图中各顶点的关系是用边来表示（边集可以为空）。
　图的基本概念
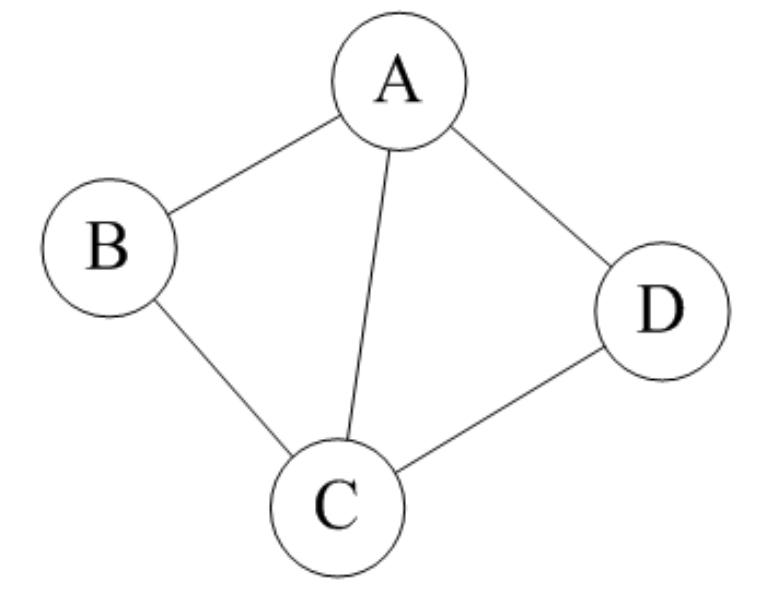
　 （1）无向图：
如果图中任意两个顶点之间的边都是无向边（简而言之就是没有方向的边），则称该图为无向图（Undirected graphs）

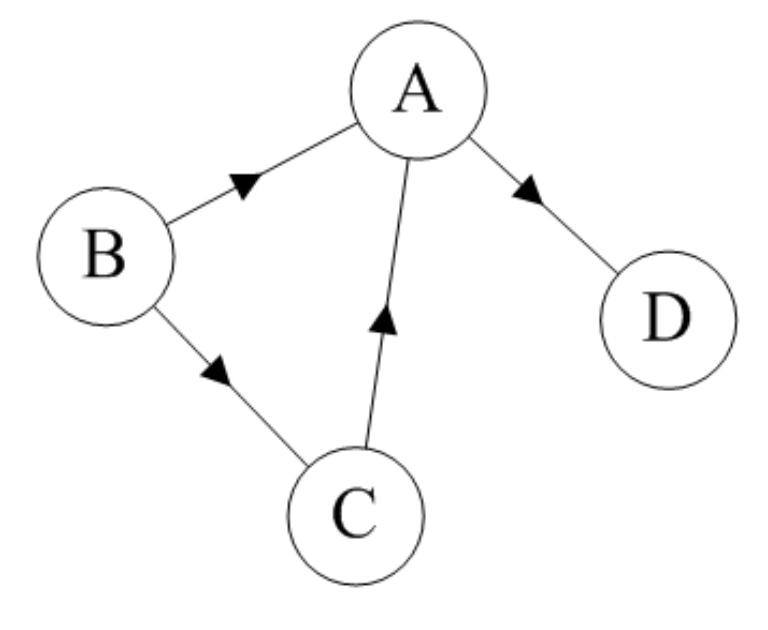
　　（2）有向图：
如果图中任意两个顶点之间的边都是有向边（简而言之就是有方向的边），则称该图为有向图（Directed graphs）。

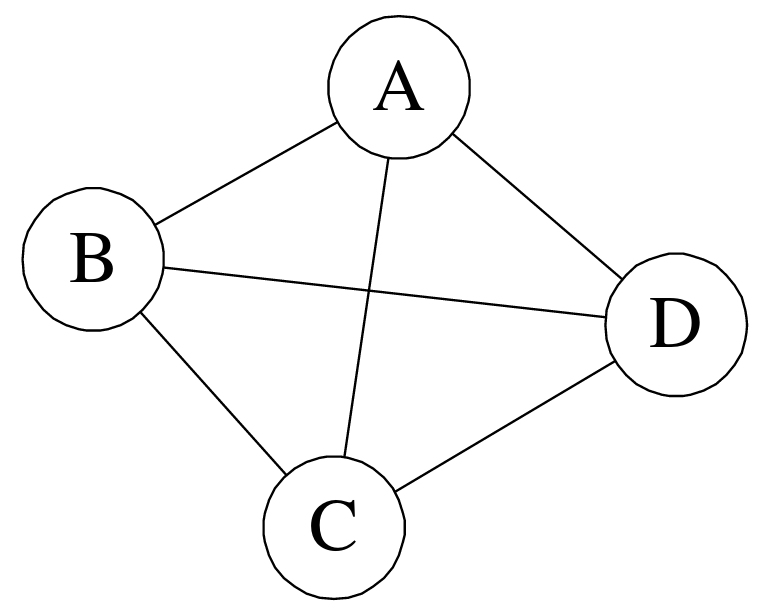
　　（3）无向完全图：
a.无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。（含有n个顶点的无向完全图有(n×(n-1))/2条边）如下图所示：

b.有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。（含有n个顶点的有向完全图有n×(n-1)条边）如下图所示：

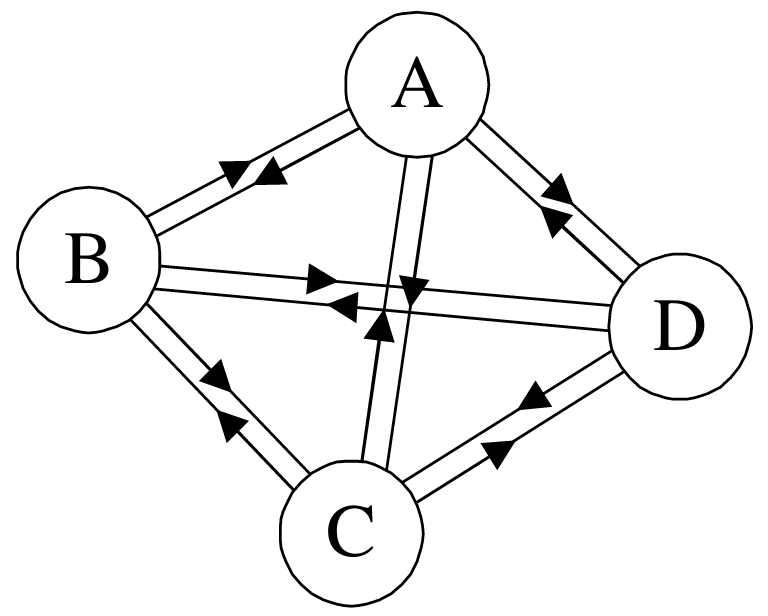
　　（4）邻接点：
在一个无向图中，若存在一条（i，j），则称顶点i和顶点j为该边的两个端点，并称它们互为邻接点。
　　（5）度：
a.顶点的度：在一个无向图中，一个顶点所关联的边的数目称为该顶点的度。
b.入度：在有向图中，以顶点j为终点的边数目，称为该顶点的入度。
c.出度：在有向图中，以顶点i为起点的边数目，称为该顶点的出度。
　　（6）路径：
在无向图中，若从顶点Vi出发有一组边可到达顶点Vj，则称顶点Vi到顶点Vj的顶点序列为从顶点Vi到顶点Vj的路径。
　　（7）简单路径：
若一条路径上除开始点和结束点可以相同以外，其他点均不相同，则称此路径为简单路径。

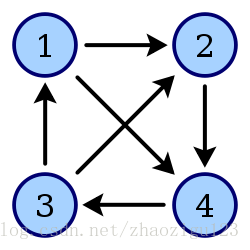
　　（8）回路和环：
若一条路径上的开始点和结束点为同一个顶点，则此路径被称为回路或环。
　　（9）连通图：
在无向图G中，任意两个顶点都是连通的，则称G为连通图。
　　（10）强连通图：
在有向图G中，任意两个顶点i和j都连通，则称图G为强连通图。
　　（12）简单回路(简单环)：
除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路。
　　（13）连通：
在无向图 G 中，从顶点 V 到顶点 S 有路径，则称 V 和 S 是连通的。
　　（14）连通分量：
无向图中的极大连通子图。
　　（15）强连通分量：
有向图中极大强连通子图称为强连通分量。

　图的存储结构
　 （1）邻接矩阵存储方法：
图的邻接矩阵是一种采用邻接矩阵数组表示顶点之间和顶点之间相邻关系的存储结构。

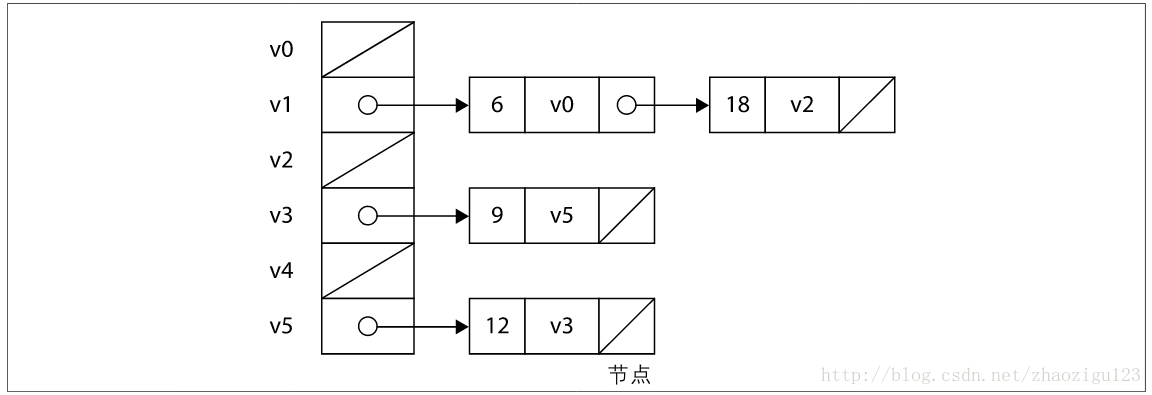
　　（2）邻接表存储方法：
图的邻接表是一种顺序与链式存储相结合的存储方法。邻接表由表头节点和表节点两部分组成，图中每个顶点均对应一个存储在数组中的表头节点。如果这个表头节点所对应的顶点存在邻接节点，则把邻接节点依次存放于表头节点所指向的单向链表中。
　图的疑难点
　　（1）拓扑排序问题：一种是“从前向后”的排序，一种是“从后向前”排。
　　（2）关键路径问题：一是什么是关键路径，二是最早时间是什么意思、如何求，三是最晚时间是什么意思、如何求。