树、二叉树

思维导图

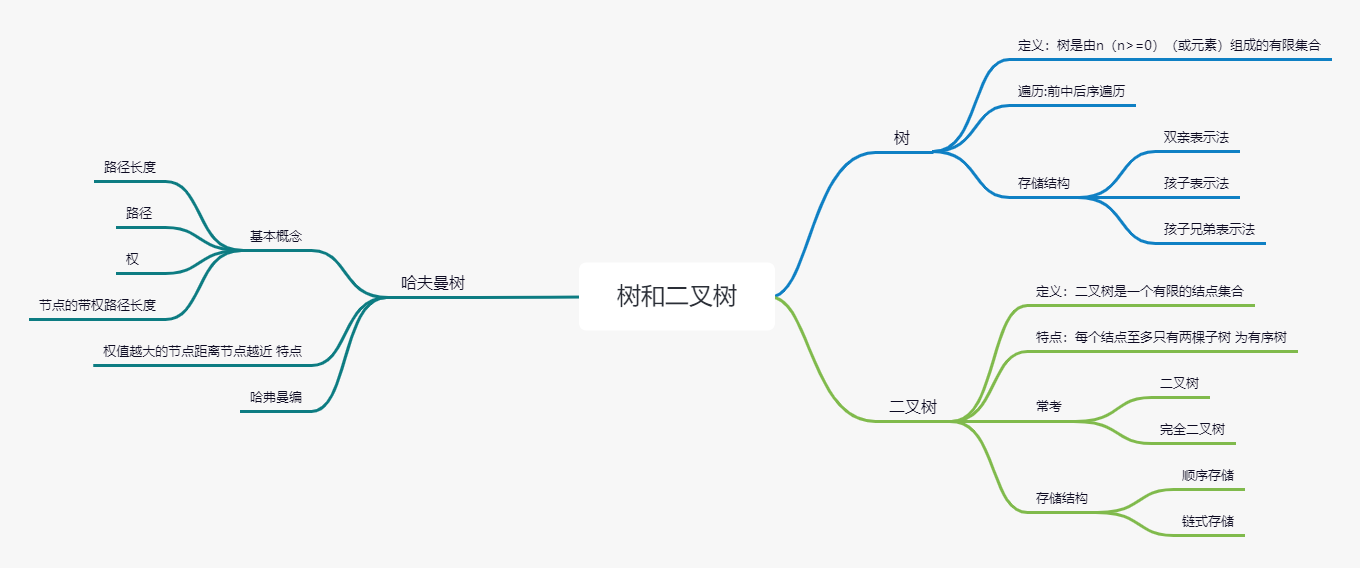
树
基本概念 ：树是一种非线性结构，常用于表示有层次关系的数据。树有多种逻辑表达方式，常用的有树形、文氏图、凹入、括号表示法。
树的基本术语
（1）结点的度与树的度：结点的度是树中某个结点的的子树的个数；树的度是树中所以结点的度中的最大值为（将度为m的树叫做m次树）
（2）分支结点与叶子结点：分支结点是度不为零的结点；叶子结点是度为零的结点
（3)孩子结点、双亲结点、兄弟结点：孩子结点就是一棵树中每一个结点的后继结点 顾名思义可以知道双亲结点、兄弟结点、子孙结点，祖先结点
（5）结点的层次和树的高度：结点层次就是从树根开始，树根为第一层接着其孩子结点为其第二层以此类推；树中结点的最大层次就是书的高度
（6）有序树无序树：树中各个结点的子树是按照一定的次序从左向右安排，次序不能随意变换这就是有序树；否则就是无序树
（7）森林：n个互不相交的树的集合
树的性质：
（1）树中的结点树等于所以结点的度数之和加一
（2）度为m的树中第i层上最多有m的i减一次方个结点
树的基本运算：
（1）先根遍历
（1）中根遍历
（1）后根遍历
二叉树
基本概念：二叉树是n (n≥0)个结点的有限集合，或者为空二叉树,即n= 0或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成，左子树和右子树又分别是—棵二叉树。
二叉树的性质：
（1）设非空二叉树中度为0、1和2的结点个数分别为n0、n1和n2，则n0 = n2+ 1(叶子结点比二分支结点多—个)
（2）二叉树第i层至多有2^(i-1)个结点(i≥1)
（3）m叉树第i层至多有m^(i-1)个结点(≥1)
（4）高度为h的二叉树至多有2-1个结点(满二叉树)
（5）高度为h的m叉树至多有(mh-1)/(m-1)个结点
完全二叉树：当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时，称为完全二叉树。完全二叉树只有最后两层可能有叶子结点，最多只有—个度为1的结点，按层序从1开始编号，结点i的左孩了为2i，右孩子为Zi+1;结点i的父节点为i12(如果有的话)is _n12」为分支结点,i>n12j为叶子结点
存储结构：
（1）顺序结构：定义一个长度为MaxSize的数组t，按照从上至下、从左至右的顺序依次存储完全二叉树中的各个结点；最坏情况：高度为h且只有h个结点的单支树(所有结点只有右孩子)，也至少需要2个h-1个存储单元（二叉树的顺序存储结构，只适合存储完全二叉树）
（2）链式结构：n个结点的二叉链表共有n+1个空链域
哈夫曼树：
定义：在n个带权叶子结点构成的所以二叉树中，带权路径长度WPL最小的二叉树称为哈夫曼树（采用顺序存储结构）
基本概念：
（1）路径:两个结点之间路过的分支
（2）结点的路径长度:路径上的分支数
（3）树的路径长度:从树根到每一个结点的路径长度
（4）结点数目相同的二叉树，完全二叉树路径长度最之和。记作TL。
（5）权︰将树中结点赋给一个有着某种含义的数值，则这个数值成为该结点的权
（6）结点的带权路径长度:从根结点到该结点之间的路径长度与该结点权的乘积
（7）树的带权路径长度:树的所有叶子结点的带权路径长度之和。记作WPL
哈夫曼树以及应用：
1.构造哈夫曼树
贪心算法:首先选择权值较小的叶子
2.哈夫曼算法:
（1）构造森林全是根
（2）选用两小造新树
（3）删除两小添新人
（4）重复2、3剩单根
3.合并n-1次，产生n-1个新结点