二叉树的存储结构
二叉树的存储结构
二叉树可使用顺序结构和链表结构两种存储结构
顺序结构
顺序结构实现二叉树时,采用一个一维数组来存储所有结点,需要将所有结点按照在树中的位置安排成一个恰当的序列,使其能反应结点之间相互的逻辑关系,通常使用编号的方法;
具体方法:
将二叉树中所有结点按照完全二叉树进行编号,然后使用一维数组存储,同时使结点编号与数组下标相同,如编号为1的节点存储在数组下标为1的位置;该方法称为以编号为地址的策略
案例1(完全二叉树):
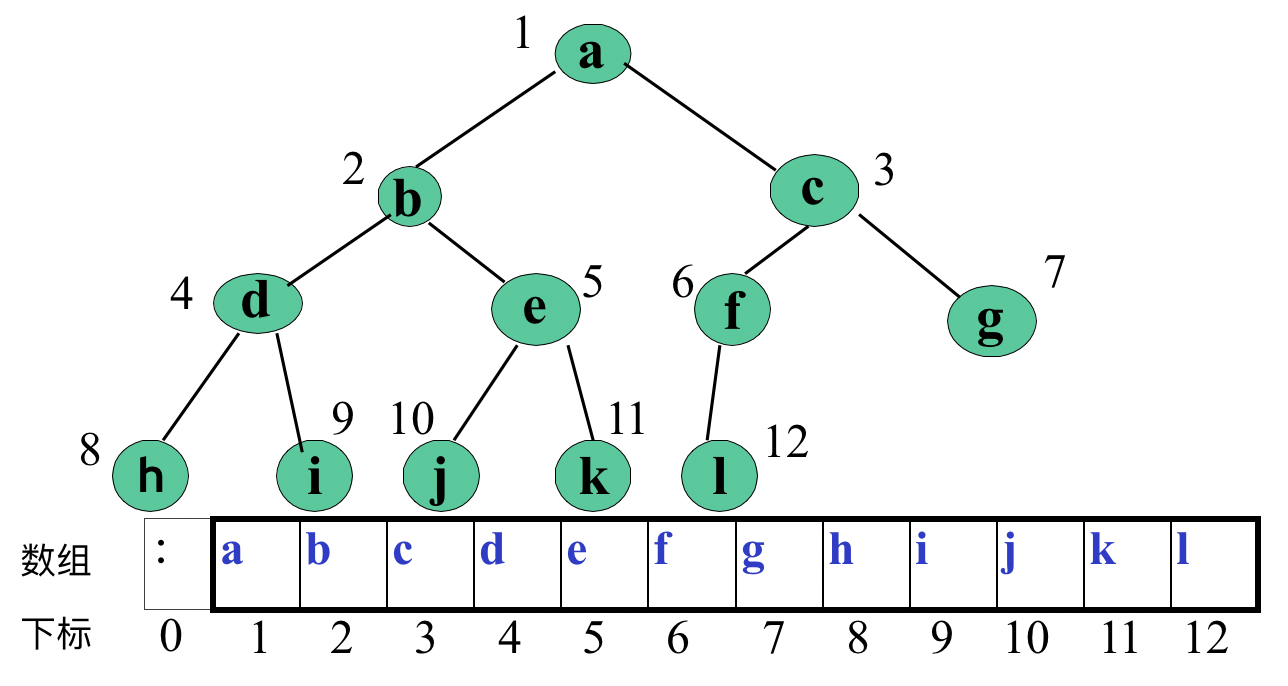
若二叉树为完全二叉树则上述方法,可以很好的利用存储空间,基本没有浪费,且对于结点的查找是很方便的;
案例2(一般二叉树):
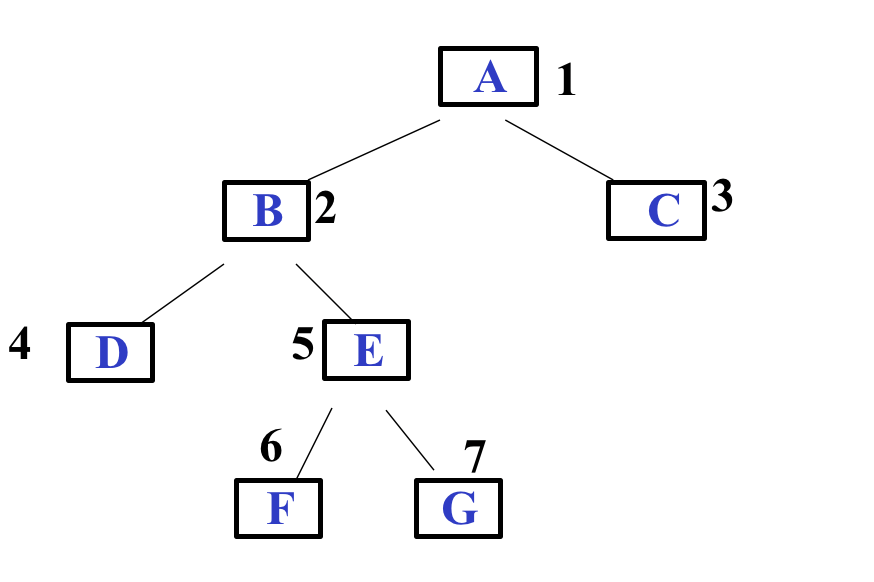
当二叉树为一般二叉树时,如想要使用顺序结构存储则必须增加虚拟结点,使其变为完全二叉树,像下面这样:
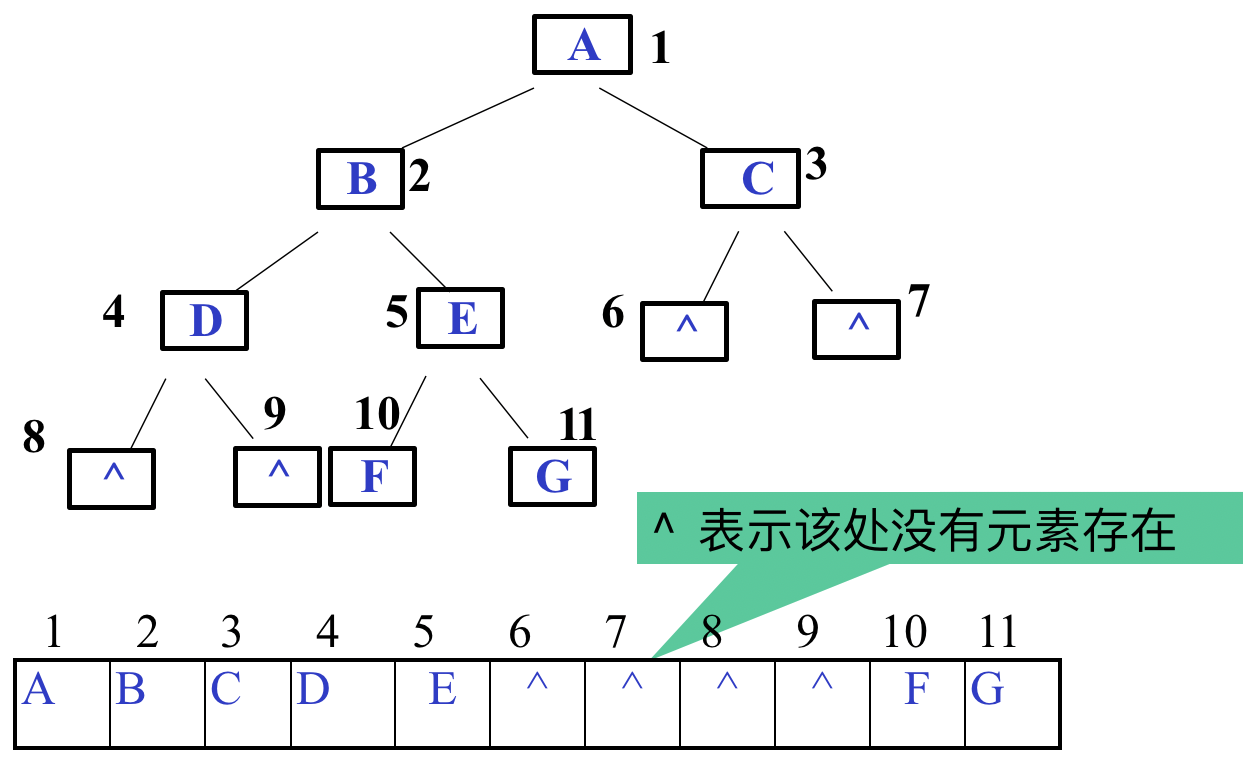
这样一来则需要浪费一部分存储空间,极端情况下,若二叉树是一分叉的(每个节点只有一个子节点),将造成极大的空间浪费
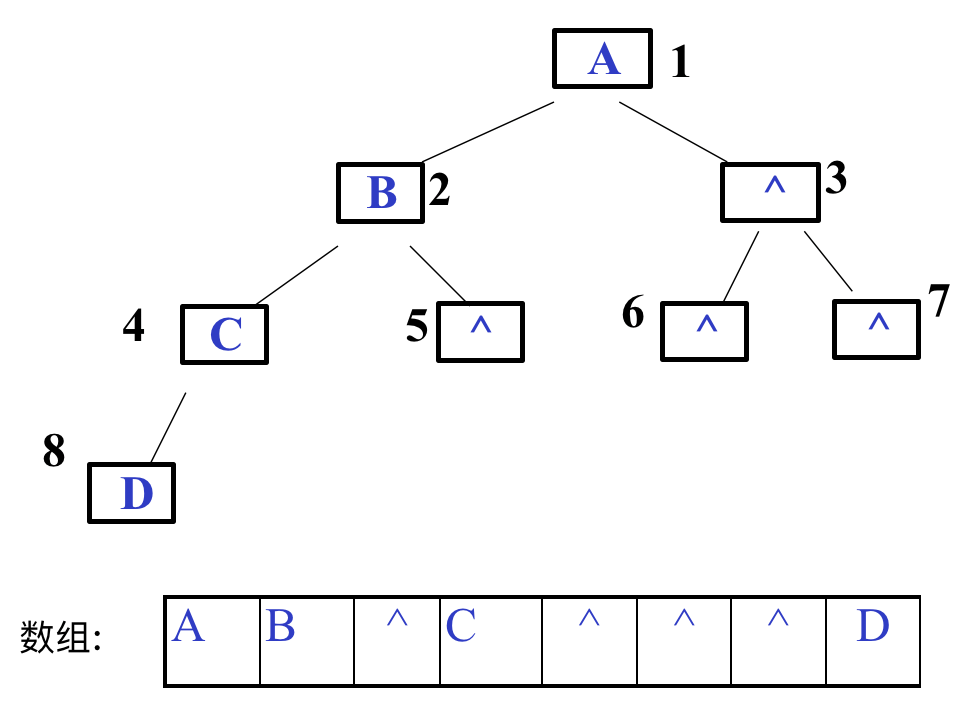
链式存储结构
链式存储结构,分为两种二叉链表和三叉链表
二叉链表
每个结点由一个数据域和两个指针域组成,共三个部分,如下图所示

数据结构定义:
typedef struct btnode {
DataType data;
struct btnode *lchild,*rchild;
}*BinTree;
案例:
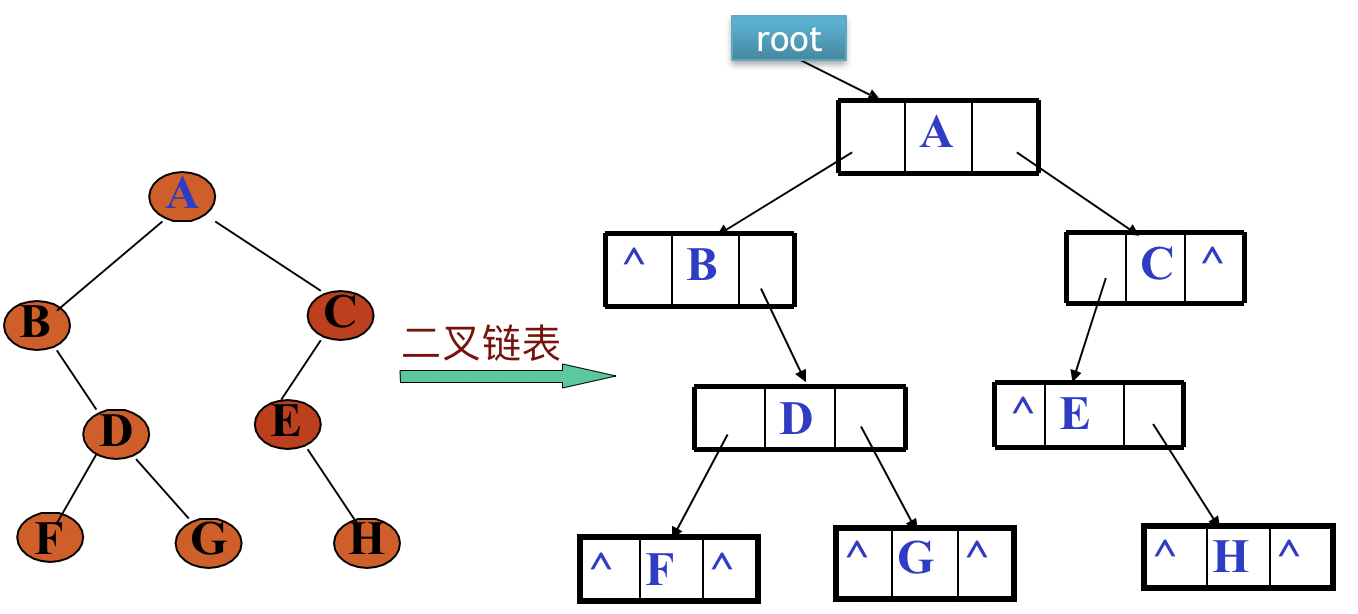
由于使用了链式存储结构,在插入或删除结点时效率比顺序结构更好;并且不会造成较大的空间浪费;
特性:
- n个结点组成的二叉树共有2n个指针域,其中有n-1个指向左右子结点的非空指针域,(两个节点关联需要一个指针域,以此类推3个结点关联需要2个指针域)和n+1个空指针域
- 已知某结点地址求其子结点方便,求其父节点则需要从头开始遍历
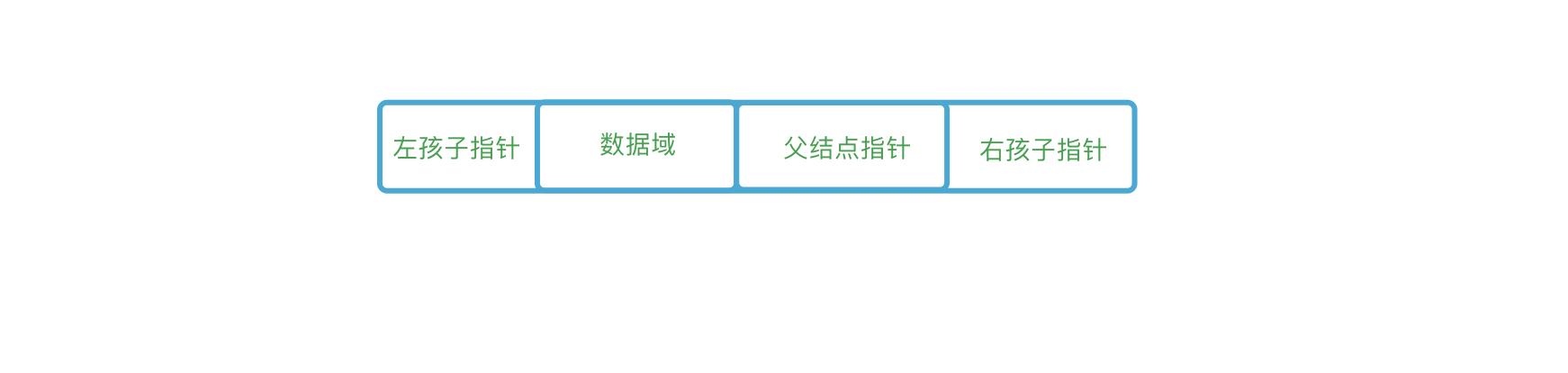
三叉链表
由于二叉链表查找父结点需要遍历所有结点,效率较低,若对于经常需要查询父结点的二叉树,则可以使用三叉链表来提高效率,三叉链表在二叉链表的基础上增加了一个parent指针域,如下图所示:
案例:
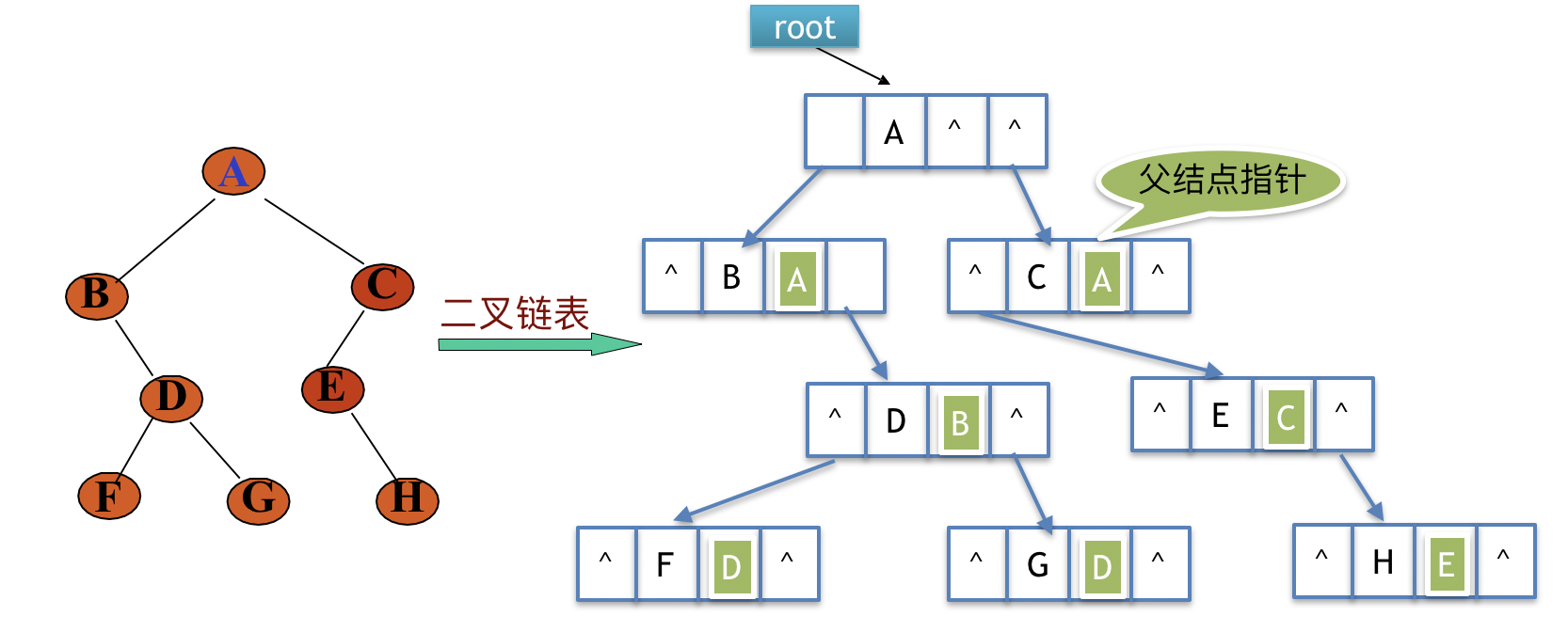 可以看出三叉链表与二叉链表没有太大区别,牺牲一些空间换来了查询父结点的效率;
可以看出三叉链表与二叉链表没有太大区别,牺牲一些空间换来了查询父结点的效率;


