树和二叉树
树和二叉树
什么是树结构
树形结构是一类重要的非线性结构,树形结构中结点之间具有分支,并具有层次结构关系,类似于自然界中的树; 生活中也大量存在,如家谱,行政组织结构都可以用树形象的表示;
既然自然界中存在这种结构的数据,那计算机中也需要相应的数据结构来存储; 在计算机领域树结构也有着广泛的应用,如编译程序中使用树表示语法结构,数据库中用树(索引)来组织数据,分析算法行为时可用树描述其指向过程;
树的定义
树是n (n>=0)个结点的有限集,记做T;当结点数n为0时称为空树
且满足以下特性:
当结点数n大于0时,有且仅有一个特定的根结点;
除根结点外的其余结点可分为m(m>=0)个互不相交的子集,T1.T2....Tn,其中每个子集Ti又是一棵树,称之为子树
任意一棵树的结点数=分支数+1
树的逻辑表示
常见的表示法有如下四种:
-
一般表示法
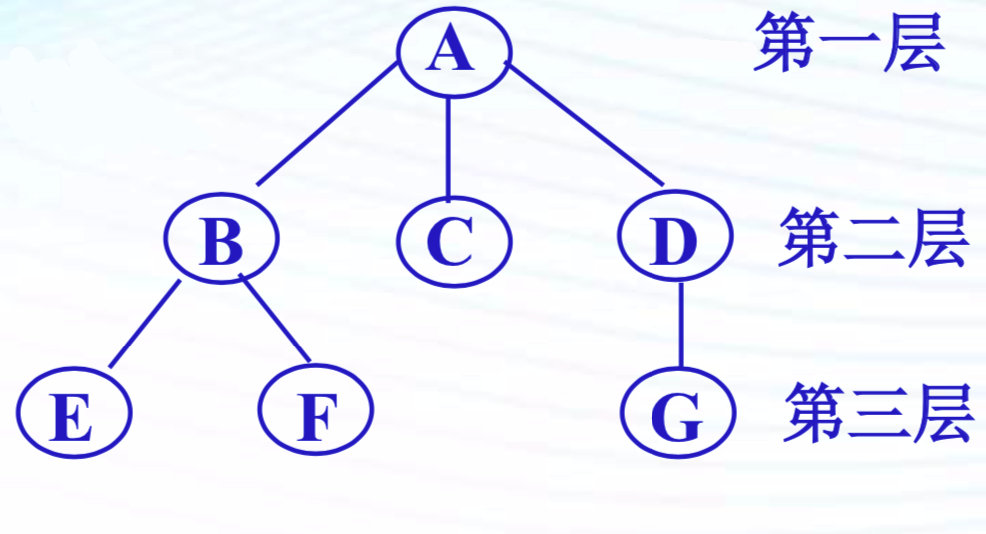
-
文氏图法
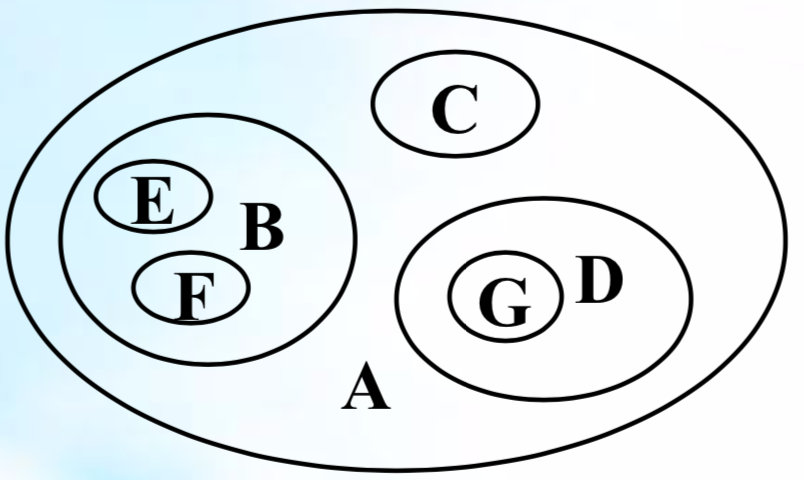
-
凹入表示法
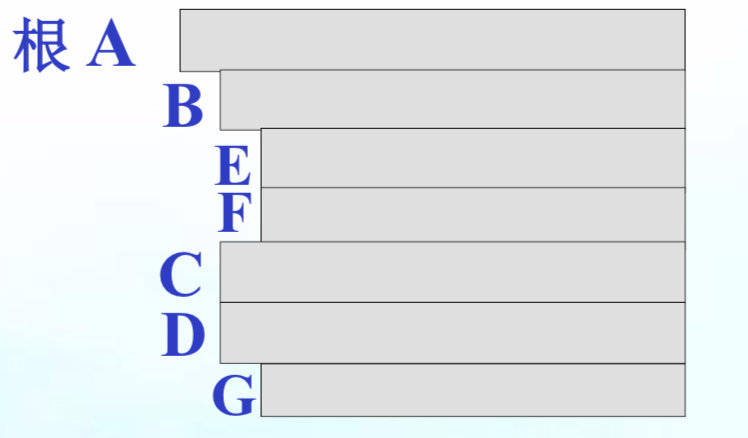
-
嵌套括号法:
(根(子树,子树,子树))
(A(B(E,F),C,D(G)))
其中第1,4两种最为常见;
树的相关术语
-
结点
- 由一个数据元素及若干个指向其他结点的分支组成
-
度
- 结点的度: 该结点的子树数(分支数==子结点数)
- 树的度: 树中所有结点的度的最大值
-
叶子结点(终端结点)
- 度为0的结点(没有孩子)
-
分支结点(非终端结点)
- 度不为0的结点(有孩子)
-
孩子(子结点)
- 结点的子树的根结点,称为该结点的孩子
-
双亲(父结点)
- 一个结点是该结点所有子结点的双亲
-
祖先
- 结点的祖先是指从根结点到该结点的一条路径上的所有结点
-
子孙
- 从某结点到叶结点的路径上所有结点(包括叶结点),称为该结点的子孙
-
兄弟
- 具有相同父结点的结点
-
结点的层次(计算方式)
- 从根算起,根为第一层,根结点的所有孩子都在第二层; L层的所有结点的孩子都在L+1层;
-
堂兄弟
- 其双亲不同但处于同一层的结点
-
树的深度(高度)
- 树中结点的最大层次;
-
有序/无序树
- 树中各个节点的子树从左到右是有次序的(升序/降序),不能互换,称为有序树
- 树中各个节点的子树从是无次序的可以互换,称为无序树
-
森林
- 是m(m>=0)棵树的集合
树的基本运算
- 求根Root(T):求树T的根结点;
- 求双亲Parent(T,X):求结点X在树T上的双亲; 若X是树T的根或X不在T上,则结果为一特殊 标志(NULL);
- 求孩子Child(T,X,i):求树T上结点X的第i个孩子 结点;若X不在T上或X没有第i个孩子,则结 果为一特殊标志(NULL);
- 建树Create(X,T1,...,Tk),k>1:建立一棵以X为根, 以T1,...,Tk为第1,...,k棵子树的树;
- 剪枝Delete(T,X,i):删除树T上结点X的第i棵子 树;若T无第i棵子树,则为空操作;
- 遍历TraverseTree(T):遍历树,即访问树中每个 结点,且每个结点仅被访问一次。
二叉树
二叉树是树的一种特殊情形,二叉树在树结构的应用中起着非常重要的作用,因为二叉树有许多良好的性质和简单的物理表示,且任何树都可以与二叉树相互转换,这极大降低了树的存储结构及其运算复杂度;
二叉树的定义
二叉树是由n(n>=0)个节点组成的有限集合,当结点数n为0时称为空二叉树,当结点数n>0时,每个节点最多有两个子树,称为左子树和右子树
特点
-
每个节点最多只能有两个子树
-
子树有左右之分,且次序不能颠倒
-
即使只有一个子树也必须明确左右,这是与树最主要的差别
-
二叉树与树的对比:
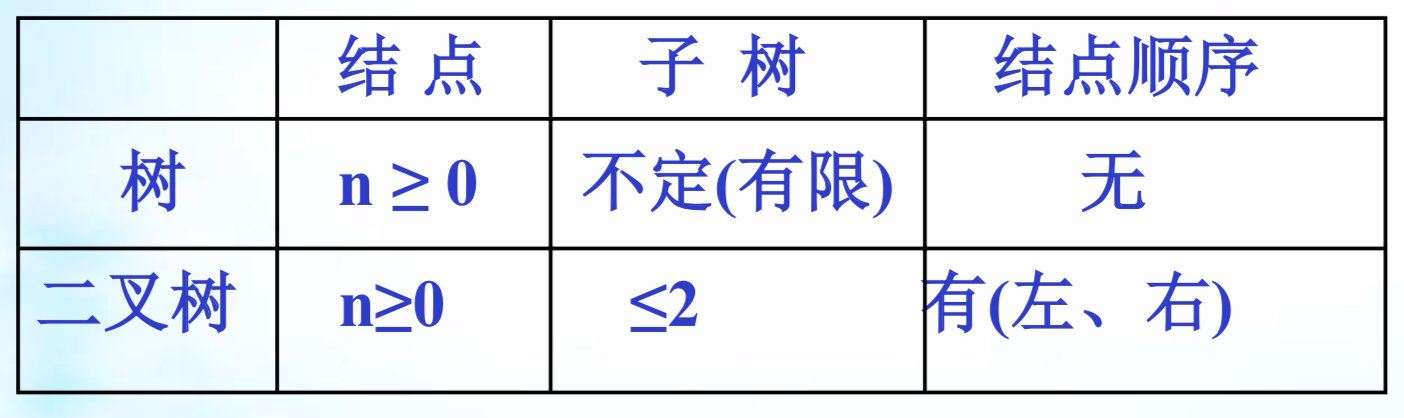
五种基本形态
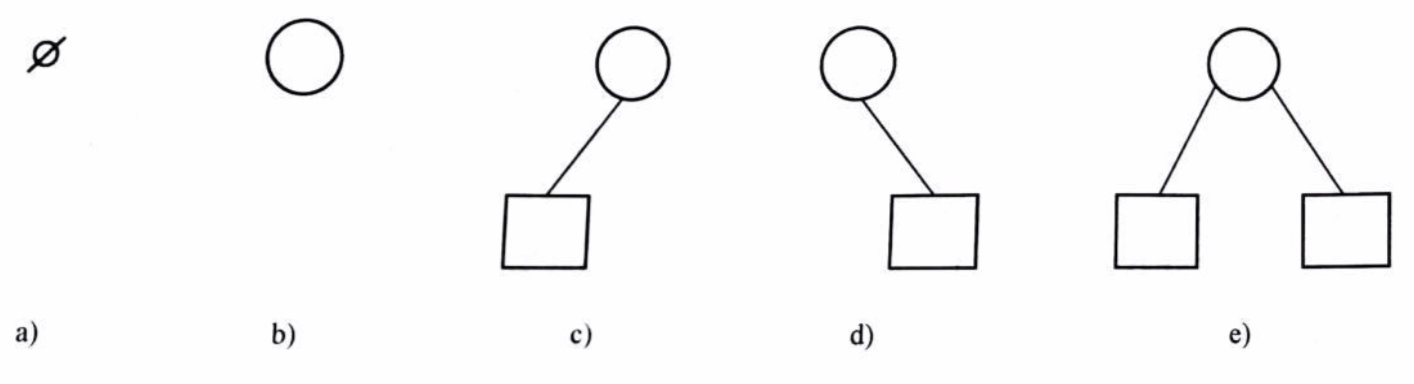
a. 空二叉树
b. 左右子树均为空的二叉树
c. 右子树为空的二叉树
d. 左子树为空的二叉树
b. 左右子树都非空的二叉树
二叉树的性质(*)
二叉树之所以重要,因其具备以下5个重要特性
1.在二叉树的第i(i>=1)层上最多有2^(i-1)个结点
根据该性质可通过层数计算该层结点数量
2.深度为k(k>=1)的二叉树中最多有(2^k)-1
根据该性质可通过深度计算总节点数
3.任意一颗二叉树,如果其叶子结点数为n0,度为2的节点数为n2,则n0 = n2 + 1
证明:
度为0的结点记为n0,度为1的结点记为n1,度为2的结点记为n2
设总结点数为1,即只有根节点,此时满足n0 = n2+1;
若有总结点数为n的二叉树,设n = k时满足n0 = n2+1;
当总节点数n=k+1,即增加一个新节点,设为s,
若新节点s的的父节点为叶子结点(无子节点),则增加后叶子数n0不变,n2也不变,此时仍满足n0 = n2+1
若新节点s的的父节点为有一个孩子的结点,则增加后叶子数n0 = n0+1,n2=n2+1,此时仍满足n0 = n2+1,
故n=任意值均满足n0 = n2+1
4.具有n个节点的完全二叉树的深度为floor(log2n)+1
意为:以2为底n的对数向下取整后+1
根据该性质对于完全二叉树,可通过结点数求树的深度
5.若对有n个节点的完全二叉树的结点从1开始按层编号(从1层到最后一层,每层从左到右)则树中任意节点i(1<=i<=n)具有以下特性:
- 若i = 1,则结点i是二叉树的根,无双亲节点
- 若i > 1,则i结点的双亲Parent是编号为floor(i/2)的节点
- 如果2*i<=n,结点i的左孩子节点编号为
2 * i,否则结点i无左孩子节点,且i为叶子节点 - 如果2*i+1<=n,结点i的右孩子节点编号为
2 * i + 1,否则结点i无右孩子节点
根据该性质,可方便的判断节点是否是根节点,求父节点,求左/右子节点,判断是否为叶子结点
二叉树的分类
-
满二叉树
深度为k(k>=1),且有(2^k)-1个结点的二叉树.
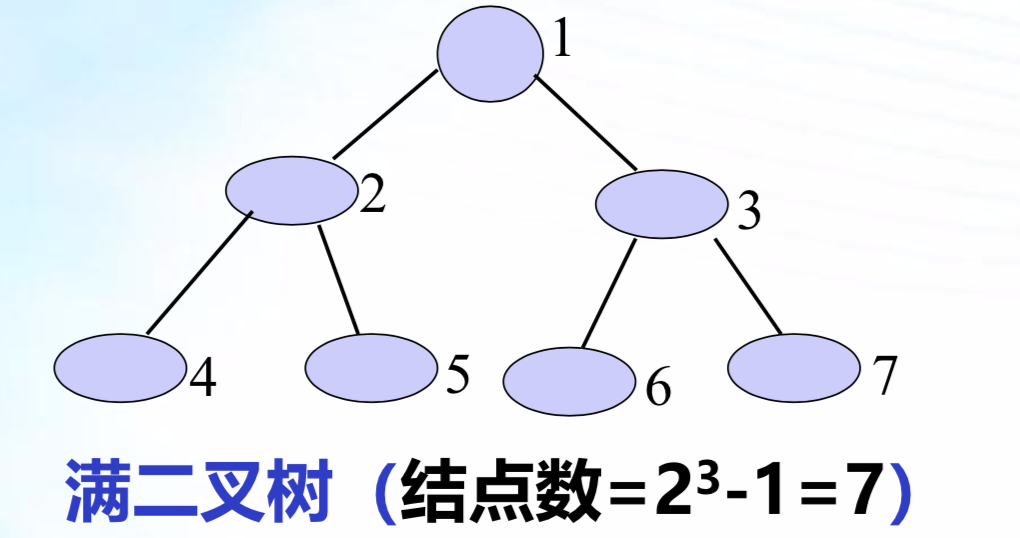
即:叶子结点的上一层中所有结点的度均为2的二叉树为满二叉树,
-
完全二叉树
深度为K的二叉树中,K-1层是满的,且K层结点是左连续的(结点编号是连续的),如图:
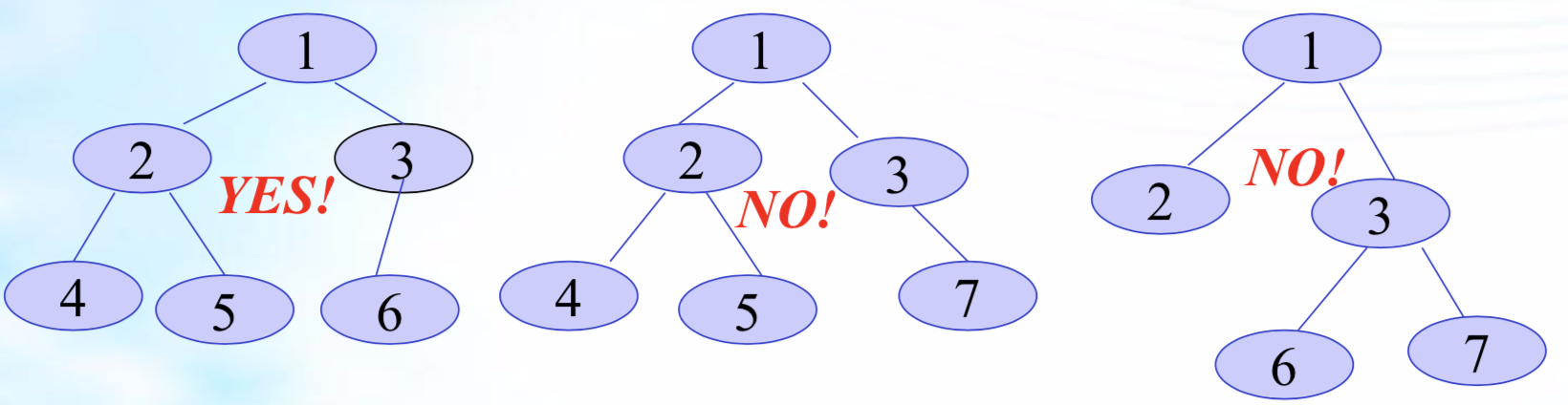
即:倒数第二层是满的,且最后一层结点是连续的;
满二叉树是完全二叉树的特殊情形
二叉树的基本运算
-
初始化Initial(BT):建立一颗空二叉树
-
求双亲Parent(BT,X):求二叉树BT上节点X的双亲节点,若X为BT的根或X不在BT上,结果为NULL;
-
求左孩子LChild(BT,X),右孩子RChild(BT,X):求二叉树BT上结点X的左/右孩子; 若X为叶子节点或X不在BT上,结果为NULL;
-
建二叉树Create(BT):建立一棵二叉树BT
-
遍历
每个节点被访问一次,且每个节点仅访问一次,有四种不同的遍历方式
- 先序遍历(根左右)
- 中序遍历(左根右)
- 后续遍历(左右根)
- 层次遍历(按层次)


