算法Algorithm
什么是数据结构？
数据结构就是指一组数据的存储结构
什么是算法？
算法就是操作数据的一组方法
复杂度分析：
要衡量代码的执行效率，则需要用到时间、空间复杂度分析。一般使用（大O复杂度表示法）
1、时间复杂度
所有代码的执行时间与每行代码的执行次数是成正比的，而每行代码的执行次数和数据规模n也是成正比的。
大O时间复杂度表示实际上并不具体表示代码真正的执行事件，而是表示代码执行时间随数据规模增长的变化趋势，所以也叫做渐进时间复杂度，简称时间复杂度。
时间复杂度分析：
1）只关注循环执行次数最多的一段代码
大O复杂度表示法只是表示一种变化的趋势，通常可以忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级就可以了。所以在分析一个算法的事件复杂度的时候，循环执行次数最多的那段代码的执行次数与数据规模n的量级关系就是整个算法的时间复杂度
2）嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
常见的几种时间复杂度：
O(1) < O(logN) < O(N) < O(NlogN) < O(N²) < O(2^N) < O(N!)
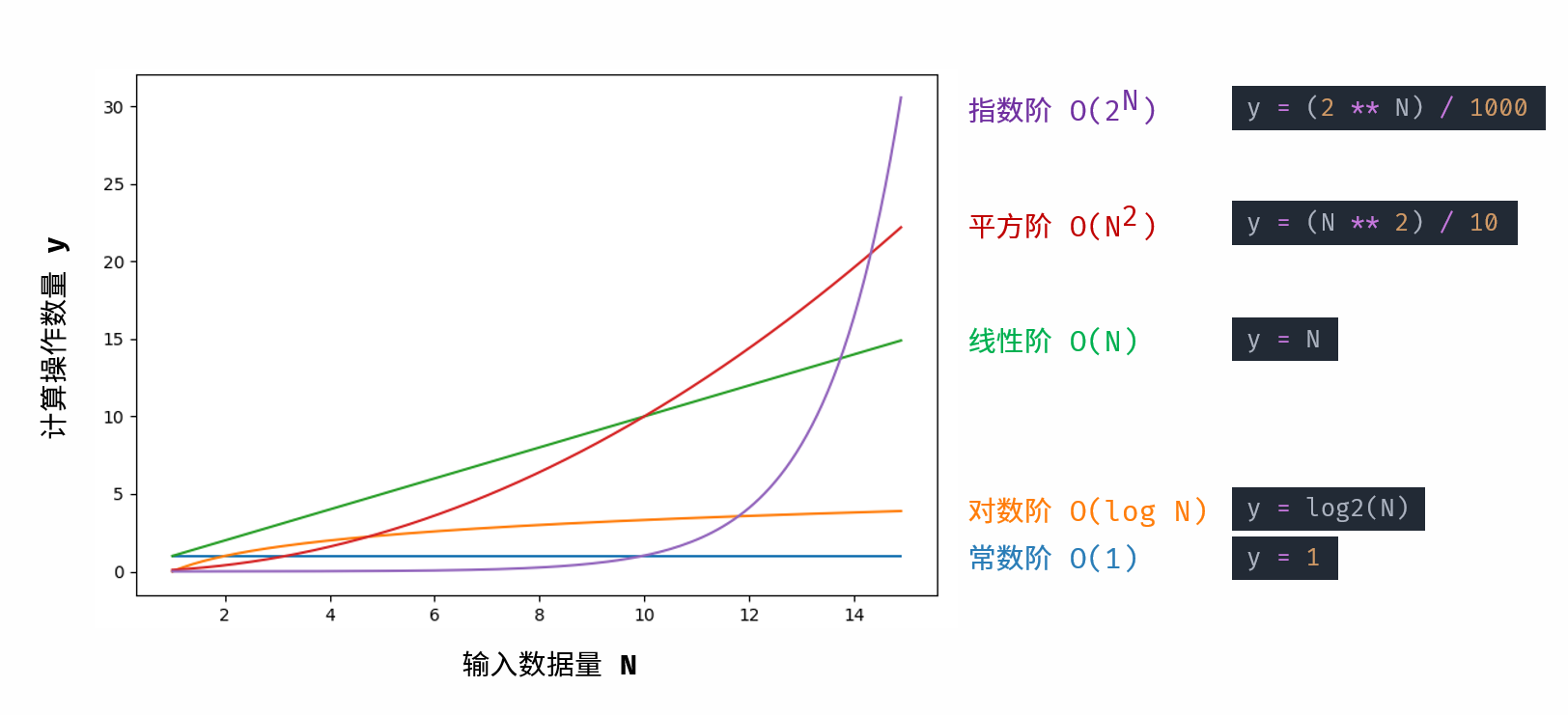
O(1)：只要代码的执行时间不随着n的增大而增长，这样的代码的时间复杂度都是O(1)。一般情况下，只要算法中不存在循环语句、递归语句，不管有多少行代码，其时间复杂度都是O(1)。
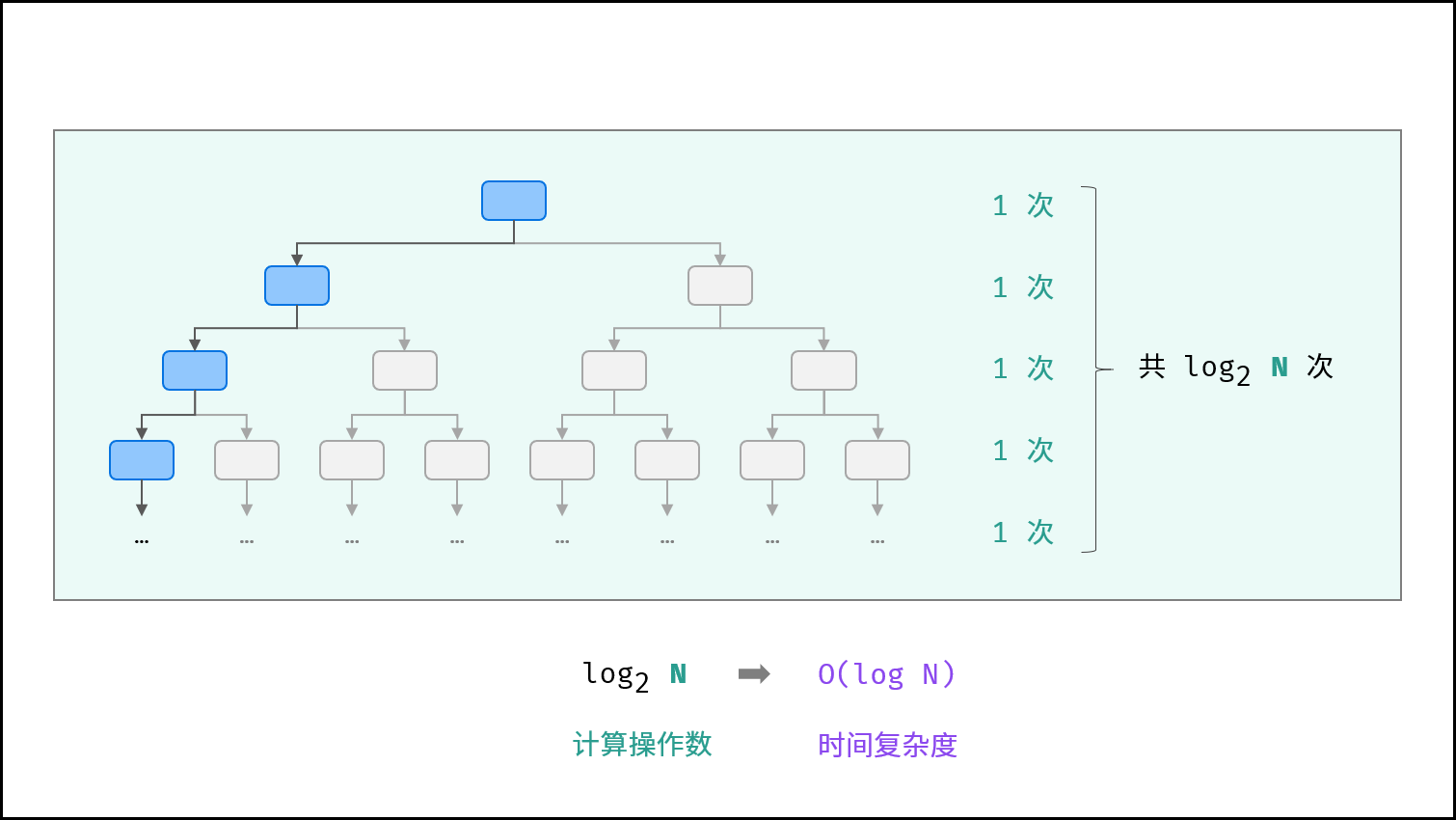
O(logn)：代码执行的次数是一个等比数列，随着n的增长，代码执行的次数 呈对数阶的增长
对数阶与指数阶相反，指数阶为 『每轮分裂出两倍的情况』，而对数阶是『每轮排除一半的情况』，对数阶常出现于二分法、分治等算法中，体现着一分为2，或一分为多的算法思想。
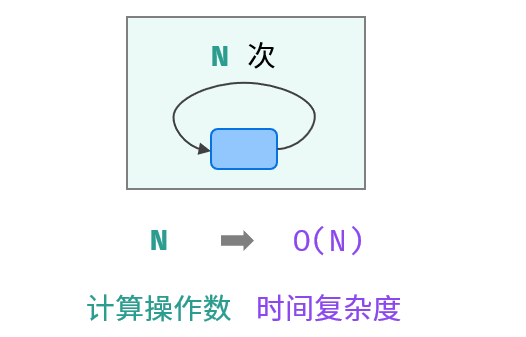
O(n)：循环运行次数与n 大小呈线性关系，时间复杂度为 O(N)
O(nlogn)：两层循环相互独立，第一层和第二层时间复杂度分别为 O(logN) 和 O(N)，则总体时间复杂度为 O(N \log N)O(NlogN)
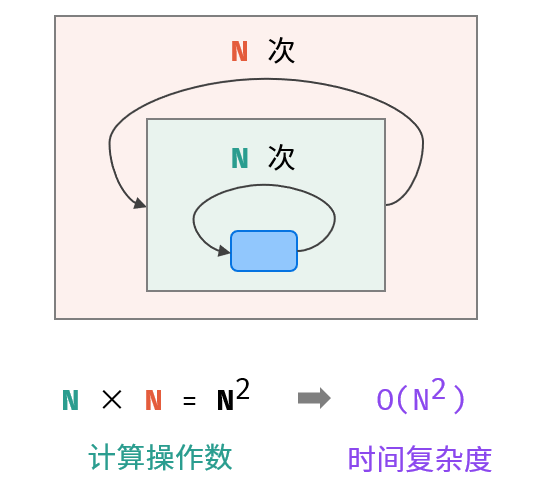
O(n²)：两层循环相互独立，都与 N呈线性关系，因此总体与 N 呈平方关系
O(2^N)：指数
生物学科中的 “细胞分裂” 即是指数级增长。初始状态为 1 个细胞，分裂一轮后为 2 个，分裂两轮后为 4 个，……，分裂 N 轮后有 2^N个细胞
算法中，指数阶常出现于递归
O(N!) ：阶乘
阶乘阶对应数学上常见的 “全排列” 。即给定 NN 个互不重复的元素，求其所有可能的排列方案，则方案数量为：
N * (N - 1) * (N - 2) * ⋯ * 2 * 1 = N!
阶乘常使用递归实现，算法原理：第一层分裂出 N 个，第二层分裂出 N−1 个，…… ，直至到第 N 层时终止并回溯
2、空间复杂度
空间复杂度的全称是渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系。
空间复杂度的分析要比时间复杂度分析简单。只需要关注代码执行时有没有申请额外的空间即可。
递归算法
递归分为两个过程，去的过程：递 ；回的过程：归。
递归需要满足的三个条件：
①：一个问题的解可以分解为几个子问题（数据规模更小的问题）的解
②：这个问题和分解之后的子问题，除了数据规模不同外，求解思路完全一样
③：存在递归终止条件（递归出口）
写递归代码的关键：找到如何将大问题分解为小问题的规律，并基于此写出递推公式，找到终止条件，最后将递推公式和终止条件转化为代码。
二次递归调用执行过程：
和二叉树的前序遍历执行流程一致。根左右
左子节点不断入栈，直到没有左子节点，再回溯输出各个右子节点。
/** * 前序遍历,根左右 */ public static void preTraversalTree(TreeNode node) { if (node == null) { return; } System.out.println(node.data); preTraversalTree(node.leftChild);// 递归I，左子节点不断入栈，直到没有左子节点，再挨个输出结果 preTraversalTree(node.rightChild); // 递归II }
执行流程如下所示：
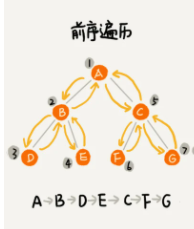
①：递归I，左子节点不断（1，2，3）入栈，直到达到出口条件（3出栈）
②：执行递归II，（4入栈），满足出口条件，4出栈
③：节点2的子节点3，4皆出栈，可计算出2的结果，因此2节点出栈
④：执行递归II，5进栈
⑤：执行递归I，6进栈，满足出口条件，6出栈
⑥：执行递归II，7进栈，满足出口条件，7出栈
⑦：节点5的子节点6，7皆出栈，可计算出5的结果，因此5节点出栈
⑧：节点1的子节点2，5皆出栈，可计算出1的结果，因此1出栈，递归结束
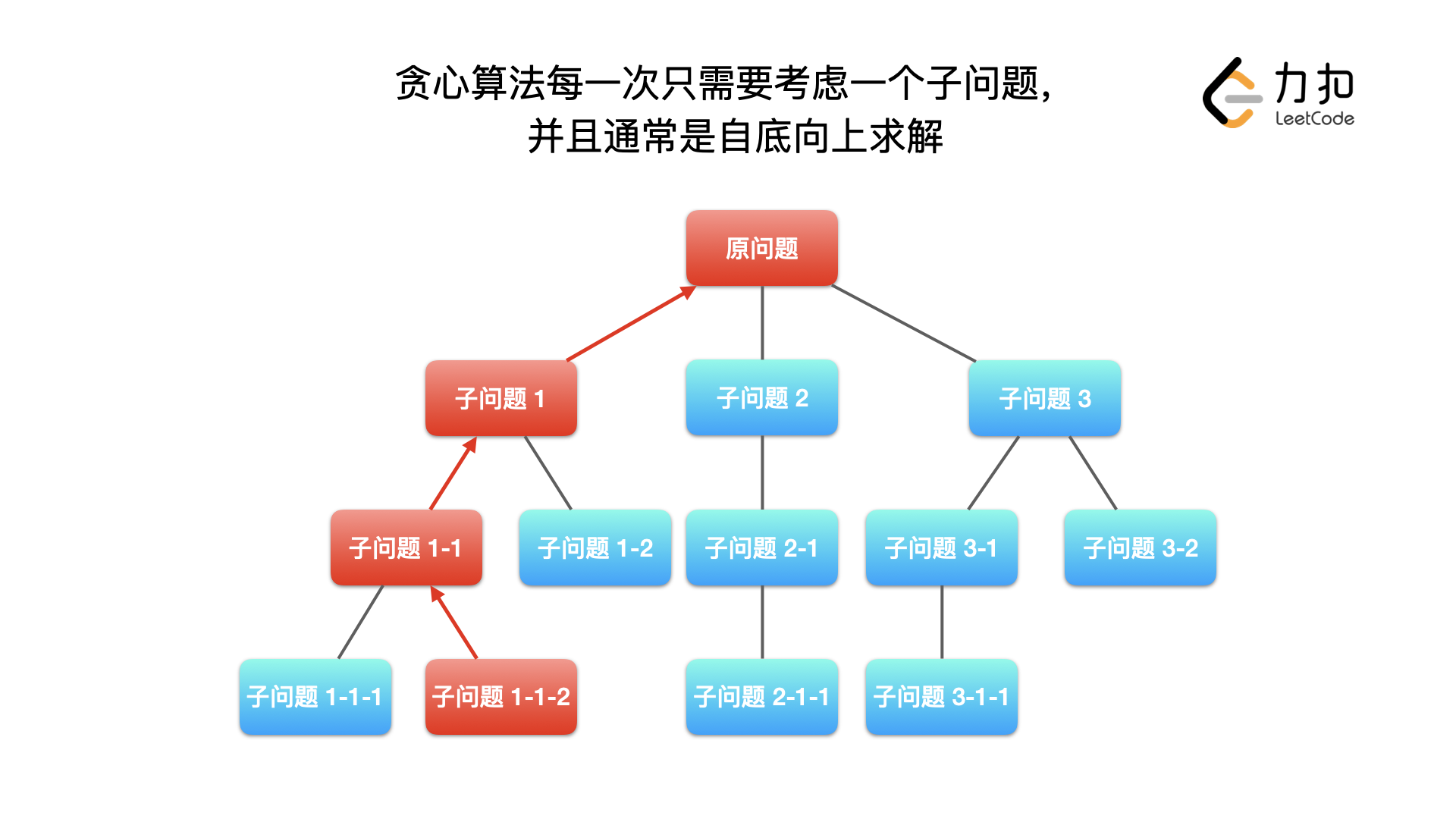
贪心算法
在对问题求解时，总是做出在当前看来是最好的选择。
也就是说不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。
因此，贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择。选择的贪心策略必须具备无后效性（即某个状态以后的过程不会影响以前的状态，只与当前状态有关。）
贪心算法有很多经典的应用，比如霍夫曼编码（Huffman Coding）、Prim 和 Kruskal 最小生成树算法、还有 Dijkstra 单源最短路径算法。
可以使用贪心算法的问题需要满足的条件：
① 最优子结构：规模较大的问题的解由规模较小的子问题的解组成，区别于「动态规划」，可以使用「贪心算法」的问题「规模较大的问题的解」只由其中一个「规模较小的子问题的解」决定
② 无后效性：后面阶段的求解不会修改前面阶段已经计算好的结果
③ 贪心选择性质：从局部最优解可以得到全局最优解
适用贪心算法的问题类型：
针对一组数据，我们定义了限制值和期望值，希望从中选出几个数据，在满足限制值的情况下，期望值最大。（如背包问题）
分治算法
分治算法（divide and conquer）的核心思想：分而治之。
也就是将原问题划分成n个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，就得到原问题的解。
分治算法一般都比较适合用递归来实现。分治算法的递归实现中，每一层递归都会涉及以下三个操作：
① 分解：将原问题分解成一系列子问题
② 解决：递归地求解各个子问题，若子问题足够小，则直接求解
③ 合并：将子问题的结果合并得到原问题的解
分治算法能解决的问题，一般需要满足下面这几个条件：
① 原问题与分解成的小问题具有相同的模式
② 原问题分解成的子问题可以独立求解，子问题之间没有相关性（这也是分治和动态规划的明显区别）
③ 具有分解终止条件，也就是说，当问题足够小时，可以直接求解
④ 可以将子问题合并成原问题，而这个合并操作的复杂度不能太高，否则就起不到减小算法总体复杂度的效果了
回溯算法
回溯的处理思想，有点类似枚举搜索。我们枚举所有的解，找到满足期望的解。为了有规律地枚举所有可能的解，避免遗漏和重复，我们把问题求解的过程分为多个阶段。每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走。
深度优先搜索算法利用的是回溯算法思想。除此之外，很多经典的数学问题都可以用回溯算法解决，比如数独、八皇后、0-1 背包、图的着色、旅行商问题、全排列等等
回溯算法非常适合用递归代码实现
动态规划
动态规划（Dynamic Programming，简称DP），通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
简单来说动态规划就是：给定一个问题，我们将它拆成一个个子问题，直到子问题可以直接解决。然后呢，把子问题答案保存起来，以减少重复计算。再根据子问题自底向上一步一步动态递推，最终得到复杂问题的最优解。
即，把问题分解为多个阶段，每个阶段对应一个决策，我们记录每一个阶段可达的状态集合（去掉重复的），然后通过当前阶段的状态集合，来推导下一个阶段的状态集合，动态地往前推进。
动态规划核心思想：拆分子问题，记住过往，减少重复计算
动态规划适合解决的问题：
问题模型：多阶段决策最优解模型
我们一般用动态规划来解决最优问题。而解决问题的过程，需要经历多个决策阶段。每个决策阶段都对应着一组状态，且下一组决策的状态是在上一组决策状态的基础上生成。所有决策阶段完毕之后，我们寻找一组决策序列，获取能够产生最终期望求解的最优值。
问题特征：
①：最优子结构
最优子结构指的是，问题的最优解包含子问题的最优解。反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。如果我们把最优子结构，对应到我们前面定义的动态规划问题模型上，那我们也可以理解为，后面阶段的状态可以通过前面阶段的状态推导出来
②：重复子问题
不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。
动态规划和递归的解法基本思想是一致的，区别在于
递归是从栈顶自上而下延伸求解的，所以也称为自顶向下的解法
动态规划从较小问题的解，由交叠性质，逐步决策出较大问题的解。是自底向上，推导求解，所以称为自底向上的解法。
动态规划有几个典型特征：最优子结构、状态转移方程、边界（初始状态）、重复子问题
如斐波那契数列中：
①：f(n-1)和f(n-2) 称为f(n)的最优子结构
②：f(n)=f(n-1)+f(n-2) 就称为状态转移方程，即最优解和最优子结构之间的关系
③：f(0)=0，f(1)=1 就是边界
④：比如 f(10)= f(9)+f(8)，f(9) = f(8) + f(7) ，f(8) 就是重复子问题
/** * 状态定义：设 dp 为一维数组，其中 dp[i] 的值代表 斐波那契数列第 i 个数字 * 转移方程：dp[i+1]=dp[i]+dp[i−1] ，即对应数列定义 f(n+1)=f(n)+f(n−1) * 边界：dp[0]=0, dp[1] = 1 ，即初始化前两个数字 * 返回值：dp[n] ，即斐波那契数列的第 n 个数字 */ public int fib(int n) { int[] dp = new int[n + 1]; dp[0] = 0; dp[1] = 1; for (int i = 2; i <= n; i++) { dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007; } return dp[n]; }
什么样的问题可以使用动态规划来解决呢？
如果一个问题，可以把所有可能的答案穷举出来，并且穷举出来后，发现存在重叠子问题，就可以考虑使用动态规划。
比如一些求最值的场景，如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等，都是动态规划的经典应用场景。
动态规划的解题思路：
动态规划的核心思想就是拆分子问题，记住过往，减少重复计算。并且动态规划一般都是自底向上的。
①：穷举分析
②：确定边界
③：找出规律，确定最优子结构（子问题的最优决策可导出原问题的最优决策）
④：写出状态转移方程
动态规划解题框架：
若确定给定问题具有重叠子问题和最优子结构，那么就可以使用动态规划求解。总体上来看，求解可分为四步：
① 状态定义：构建问题最优解模型，包括问题最优解的定义、有哪些计算解的自变量
② 初始状态：确定基础子问题的解（即已知解），原问题和子问题的解都是以基础子问题的解为起点，在迭代计算中得到的
③ 状态转移方程：确定原问题的解与子问题的解之间的关系是什么，以及使用何种选择规则从子问题最优解组合中选出原问题最优解
④ 返回值：确定应返回的问题的解是什么，即动态规划在何处停止迭代
动态规划代码框架：
dp[0][0][...] = 边界值 for(状态1 ：所有状态1的值){ for(状态2 ：所有状态2的值){ for(...){ //状态转移方程 dp[状态1][状态2][...] = 求最值 } } }
动态规划示例：背包问题
把求解过程分为n个阶段，每个阶段会决策一个物品是否放入背包中。每个物品决策（放入或不放入背包）之后，背包中的物品会有多种情况，即会达到多种不同的状态。
把每一层重复的（节点）合并，只记录不同的状态，然后基于上一层的状态集合，来推导下层的状态集合。我们可以通过合并每一层重复的状态，这样就保证每一层不同状态的个数都不会超过 w 个（w 表示背包的承载重量）
使用二维数组 states[n][w+1] 来记录每层可以达到的不同状态，n是物品的数量，w是背包的承载重量。如n=5，w=9，物品的重量分别为2,2,4,6,3时：
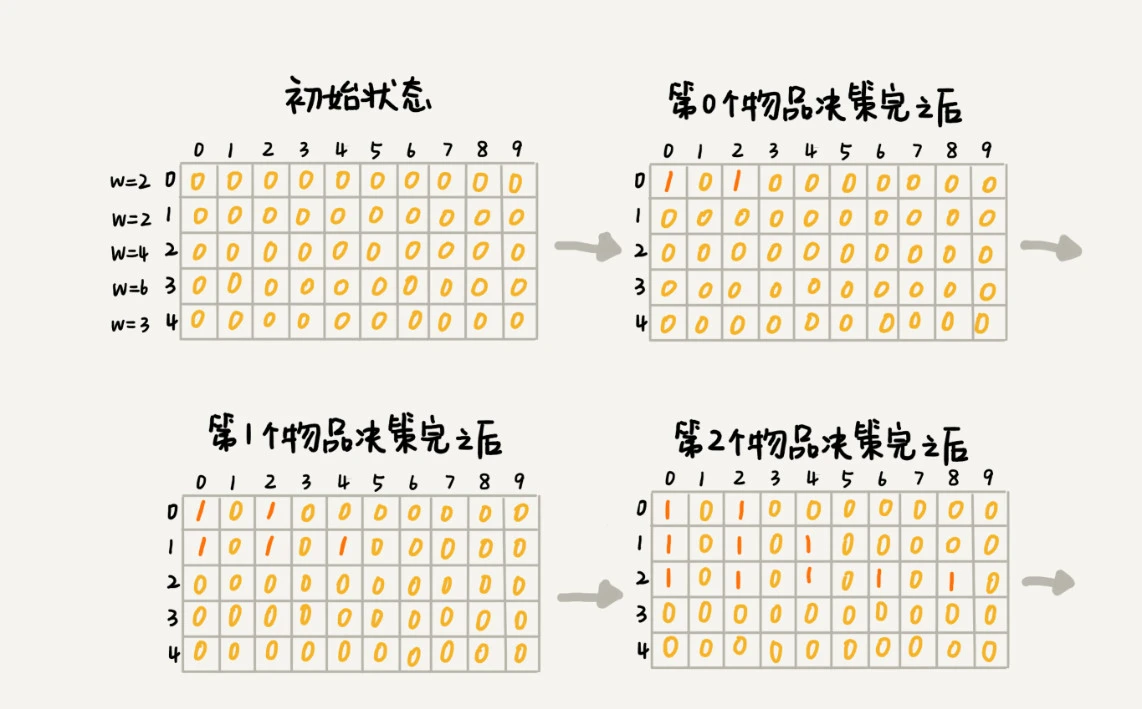
第0个（下标从0开始）的物品重量为2，要么装入背包，要么不装入背包，决策完之后，会对应背包的两种状态，背包中物品的总重量是0或2，用dp[0][0]=true,dp[0,2]=true;来表示这两种状态
第1个物品的重量也是2，基于之前物品1的状态，因此在决策完之后，有0,2(0+2 or 2+0),4(2+2)三种状态，分别用dp[1][0]=true,dp[1][2]=true,dp[1][4]=true来表示。
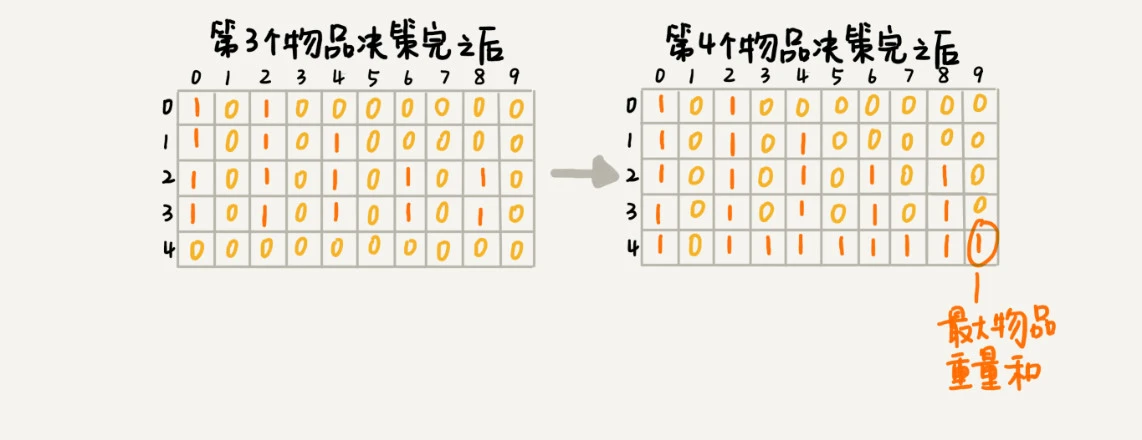
以此类推，直到决策完所有物品后，整个dp二维数组就计算好了。这时候只需要在最后一层，找一个值为true，且最接近 w(9) 的值，就是背包中物品总重量的最大值。
/** * 动态规划求解01背包问题 * * @param weight 物品重量 * @param n 物品个数 * @param w 背包可承载重量 * @return */ public int knapsack(int[] weight, int n, int w) { // 定义状态数组，默认值false boolean[][] dp = new boolean[n][w + 1]; // 特殊处理第一行的数据，作为初始状态 // 第一个物品不放入背包 dp[0][0] = true; // 第一个物品放入背包 if (weight[0] <= w) { dp[0][weight[0]] = true; } // 循环决策每个物品 for (int i = 1; i < n; ++i) { // 动态规划状态转移方程，根据上一层的决策，生成当前层的决策 for (int j = 0; j <= w; ++j) { // 不把第i个物品放入背包，下一层的值和上一层相同 if (dp[i - 1][j] == true) { dp[i][j] = dp[i - 1][j]; } } for (int j = 0; j <= w - weight[i]; ++j) { // 把第i个物品放入背包，下一层的值为上一层的值+当前物品的重量 if (dp[i - 1][j] == true) { dp[i][j + weight[i]] = true; } } } // 输出结果 for (int i = w; i >= 0; --i) { if (dp[n - 1][i] == true) { return i; } } return 0; }
贪心算法与回溯算法、动态规划的区别:
「解决一个问题需要多个步骤，每一个步骤有多种选择」这样的描述我们在「回溯算法」「动态规划」算法中都会看到。它们的区别如下：
「回溯算法」需要记录每一个步骤、每一个选择，用于回答所有具体解的问题；（有多次回溯重新选择的机会）
「动态规划」需要记录的是每一个步骤、所有选择的汇总值（最大、最小或者计数）；
「贪心算法」由于适用的问题，每一个步骤只有一种选择，一般而言只需要记录与当前步骤相关的变量的值。（一条路走到底，每次做出最优选择）
END.
