自动机

自动机是一种理想化的机器，它只是抽象分析问题的理论工具，并不具备实际的物质形态，它是科学定义的演算机器，用来表达某种不需要人力干涉的机械性演算过程。根据不同的构成和功能，自动机分成4中：

有限自动机(FA)，下推自动机(PDA),线性界限自动机，图灵机

 

1.有限自动机

DFA  M是一个五元组

M = (∑,Q,δ,q0,F)

 

∑输入符号的有限集合，

Q是状态的有限集合,

q0∈Q是初始状态

F是终止状态集合F∈Q

δ是Q与∑的直积Q×∑到Q的映射，它支配着有限状态控制的行为，有时也称为状态的转移函数。

 

DFA接受的语言:如果一个句子x对于有限自动机M有δ(q0,x)=p,p∈F,那么称句子x被M接受。被M接受的句子的全集称为由M定义的语言，或称M所接受的语言，记作T(M):

　　　　　　　　T(M) = {x|δ(q0,x)∈F}

 

正则文法与自动机的关系

若G = (Vn,Vt,P,S)是一个正则文法，则存在一个FA M = (∑,Q,δ,q0,F)，使得T(M) = L(G)

 

根据这个定理，可以用以下方法由给定的正则文法G = (Vn,Vt,P,S)构造FA

 

1).令∑ = Vt,Q = Vn∪{T},q0 = S,其中T是一个新增的非终结符;

2).如果在P中有产生式S->ξ,则F = {S,T},否则 F={T};

3).如果在P中有产生式B->a,B∈Vn,a∈Vt,则T∈δ(B,a)

4).如果在P中有产生式B->aC, B、C∈Vn，a∈Vt，则C∈δ(B,a)

5).对于每一个a∈Vt，有δ(T,a)=Ø

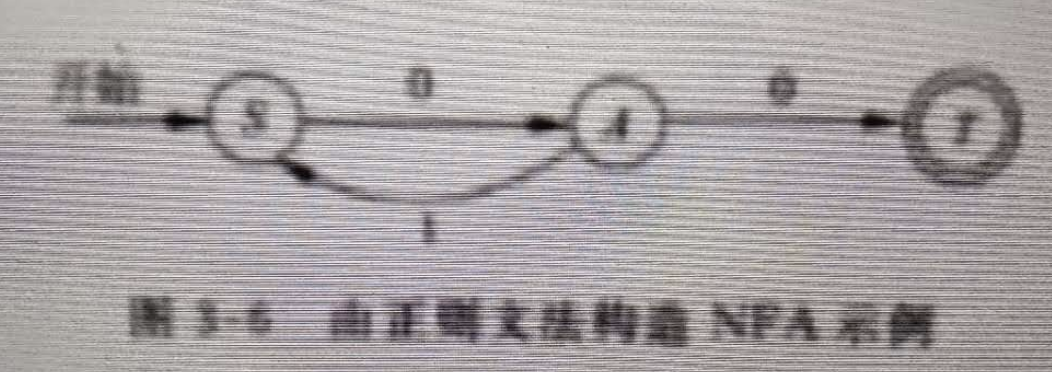
例子

给定正则文法G = (Vn,Vt,P,S),其中

Vn = {S,A}     Vt = {0,1}

P:  S->0 A  A->1 S  A->0

构造与G等价的NFA:

设NFA M = (∑,Q,δ,q0,F)，根据上述构造步骤

 

∑ = Vt = {0,1}

Q = Vn ∪ {T} = {S,A,T}

q0 = S

F = {T}

映射δ为

δ(S,0) = {A}

δ(S,1) = Ø

δ(A,0) = {T}

δ(A,1) = {S}

δ(T,0) = Ø

δ(T,1) = Ø

 

 

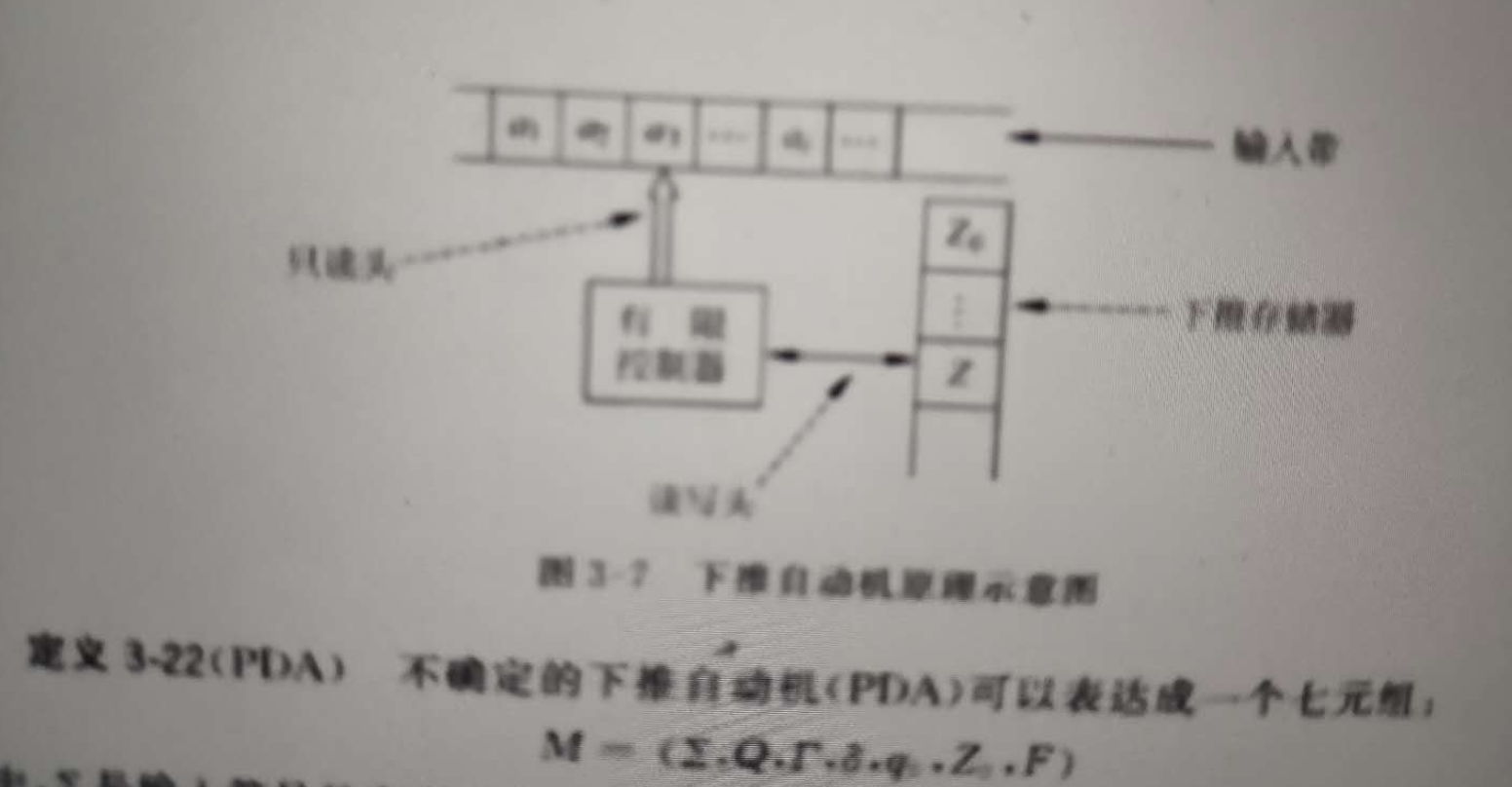
2.上下文无关文法与下推自动机

下推自动机可以看成是一个带有附加下推存储器的有限自动机，下推存储器是一个堆栈