采样

1.高斯随机数

用于获取两个独立的0均值且单位方差的正态分布的高斯变量

 

 

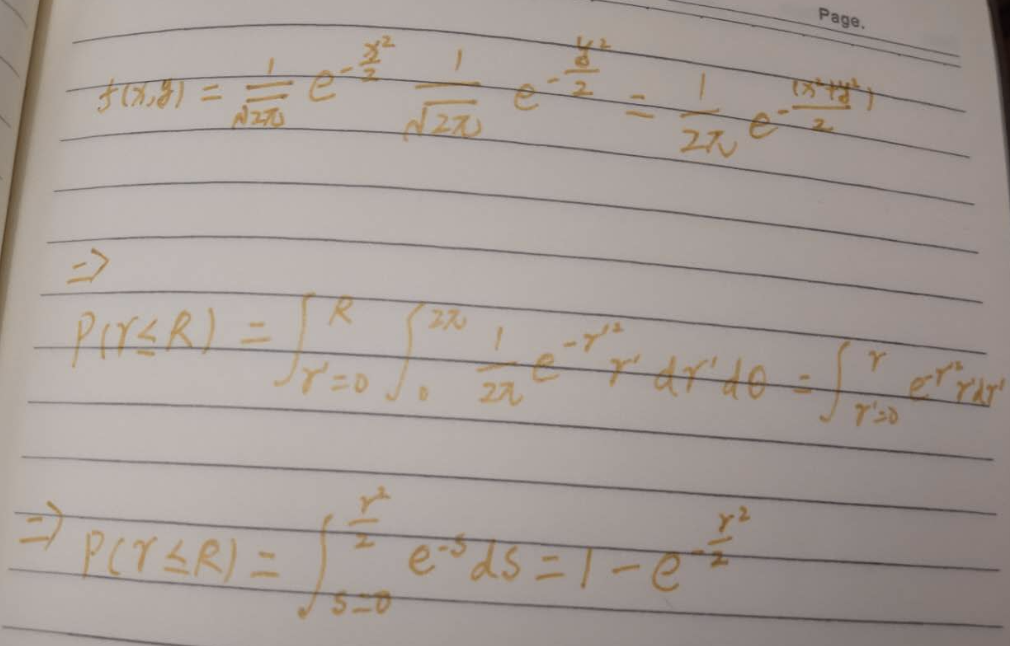
 实现步骤：

选择两个均匀分布的随机数0<=U1,U2<=1

设定thtea = 2piU1 和 r=sqrt(-2ln(U2))

那么x=rsin(thtea),y=rcos(thtea)就是0均值单位方差的独立高斯分布变量

2.蒙特卡罗

要从一个分布P(X)中采样，但是P无法直接采样，可以通过建议分布Q(X)

 

步骤:

从Q(X)中采样x‘

从(0,x')均匀分布中抽取u

如果u<p(x')/Mq(x')把x'加入样本集，否则舍弃x'

 

3.Metropolis-Hastings算法

针对目标P(x)是一个马尔可夫链，要采样p(x1),p(x2)…………

 

 

 

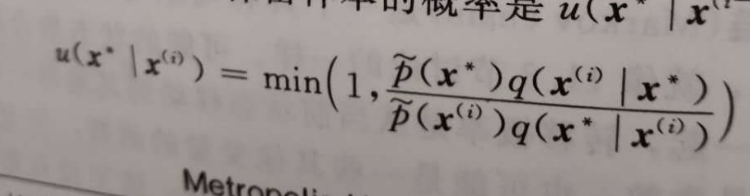
步骤:

给定一个初始值x0，

重复:

q(xi|xi-1)中采样x'

从均匀分布中采样u

如果u小于上述等式，x[i+1]=x'否则x[i+1]=x'[i]

直到有足够的样本

u=np.random.rand(N)

y = np.zeros(N)
y[0] = np.random.normal(mu,sigma)
for i in range(N-1):
    ynew = np.random.normal(mu,sigma)
    alpha = min(1,p(ynew)*q(y[i])/p(y[i])*q(ynew))
    if u[i] < alpha:
        y[i+1] = ynew
    else:
        y[i+1] = y[i]