svm支持向量机
线性可分支持向量机
指可以在两个分类的数据点之间找到一个超平面(WTx + b = 0),使得两个分类与该平面的最小距离相等,
其中离该平面最近的点就是支撑向量,即WTx+b=1或WTx+b=-1
y(xn)=WTx+b
y(xn)>0 tn=1
y(xn)<0 tn=-1
=>tn*y(xn)>0
当X向量很复杂时可以令 y(x)=WTf(x)+b
当X是一维的时候 f(x)=x
tn*y(xn)/||w|| = tn(WTf(xn)+b)/||w||
得出支持向量机目标函数
arg max (w,b){1/||w||min(n)[tn(WTf(xn)+b)]}
找到每个X到该平面的最小距离,所有距离中的最大值时对应的w,b就是我们要求的结果。
已知tn*y(xn)>=1,故目标函数可化简为 arg max(w,b)||w||*||w||/2
利用拉格朗日函数
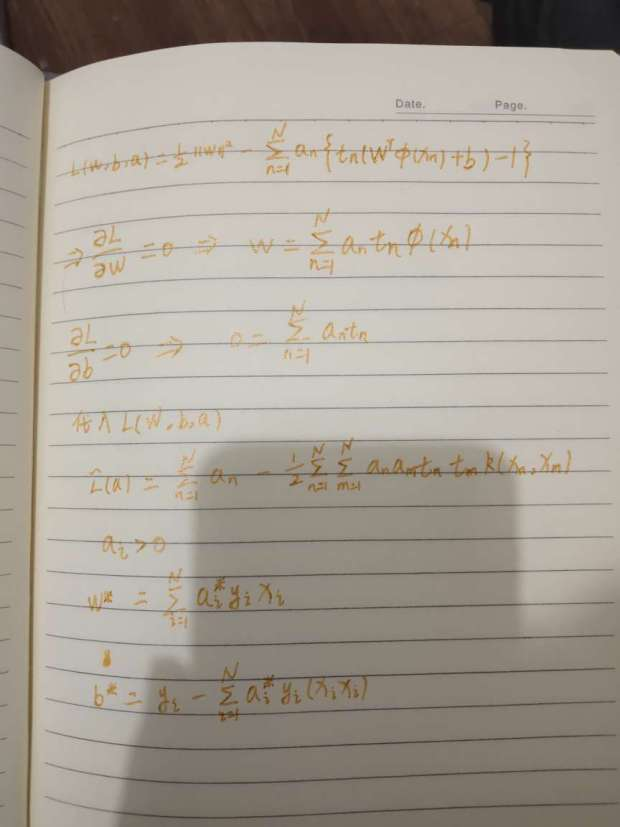
然后可以利用smo算法求解。
另外当 分类不满足线性可分时,可以令超平面 WTXi + b = 1-ζ,推到的结果与线性结果相同,只是 0<ai<C
SMO算法思想
通过观察SVM的优化目标我们可以发现其最终的目的是要计算出一组最优的alpha和常数项b的值。SMO算法的中心思想就是每次选出两个alpha进行优化(之所以是两个是因为alpha的约束条件决定了其与标签乘积的累加等于0,因此必须一次同时优化两个,否则就会破坏约束条件),然后固定其他的alpha值。重复此过程,直到达到某个终止条件程序退出并得到我们需要的优化结果。接下来,就具体推导一下SMO算法的细节。
算法数学推导
由于SVM中有核函数的概念,因此我们用Kij来表示在核函数K下向量i和向量j的计算值。现在假定我们已经选出alpha1和alpha2两个待优化项,然后将原优化目标函数展开为与alpha1和alpha2有关的部分和无关的部分:

其中c是与alpha1和alpha2无关的部分,在本次优化中当做常数项处理。由SVM优化目标函数的约束条件:

可以得到:

将优化目标中所有的alpha1都替换为用alpha2表示的形式,得到如下式子:

此时,优化目标中仅含有alpha2一个待优化变量了,我们现在将待优化函数对alpha2求偏导得到如下结果:

已知:

将以上三个条件带入偏导式子中,得到如下结果:

化简后得:

记:

若n<=0则退出本次优化,若n>0则可得到alpha2的更新公式:

此时,我们已经得到了alpha2的更新公式。不过我们此时还需要考虑alpha2的取值范围问题。因为alpha2的取值范围应该是在0到C之间,但是在这里并不能简单地把取值范围限定在0至C之间,因为alpha2的取值不仅仅与其本身的范围有关,也与alpha1,y1和y2有关。设alpha1*y1+alpha2*y2=k,画出其约束,在这里要分两种情况,即y1是否等于y2。我们在这里先来考虑y1!=y2的情况:在这种情况下alpha1-alpha2=k:

可以看出此时alpha2的取值范围为:

当y1=y2时,alpha1+alpha2=k:

可以看出此时alpha2的取值范围为:

以上,可以总结出alpha2的取值上下界的规律:

故可得到alpha2的取值范围:

由alpha_old1y1+alpha_old2y2=alpha_new1y1+alpha_new2y2可得alpha1的更新公式:

接下来,需要确定常数b的更新公式,在这里首先需要根据“软间隔”下SVM优化目标函数的KKT条件推导出新的KKT条件,得到结果如下:

由于现在alpha的取值范围已经限定在0至C之间,也就是上面KKT条件的第三种情况。接下来我们将第三种KKT条件推广到任意核函数的情境下:

由此我们可以得到常数b的更新公式:

其中Ei是SVM的预测误差,计算式为:

以上,笔者就已经把SMO算法的大部分细节推导出来了。接下来,我们可以根据这些推导对SMO算法进行实现,并且用我们的算法训练一个SVM分类器。
smo算法转载子https://www.jianshu.com/p/eef51f939ace



