【论文阅读】DSTAGNN Dynamic Spatial-Temporal Aware Graph Neural Network for Traffic Flow Forecasting

DSTAGNN Dynamic Spatial-Temporal Aware Graph Neural Network for Traffic Flow Forecasting

Info

• title: DSTAGNN: Dynamic Spatial-Temporal Aware Graph Neural Network for Traffic Flow Forecasting
• publish: ICML 2022
• url: dblp: DSTAGNN: Dynamic Spatial-Temporal Aware Graph Neural Network for Traffic Flow Forecasting. (uni-trier.de)
• corresponding author: ShiYong Lan
• first author:
  • ShiYong Lan
  • Yitong Ma

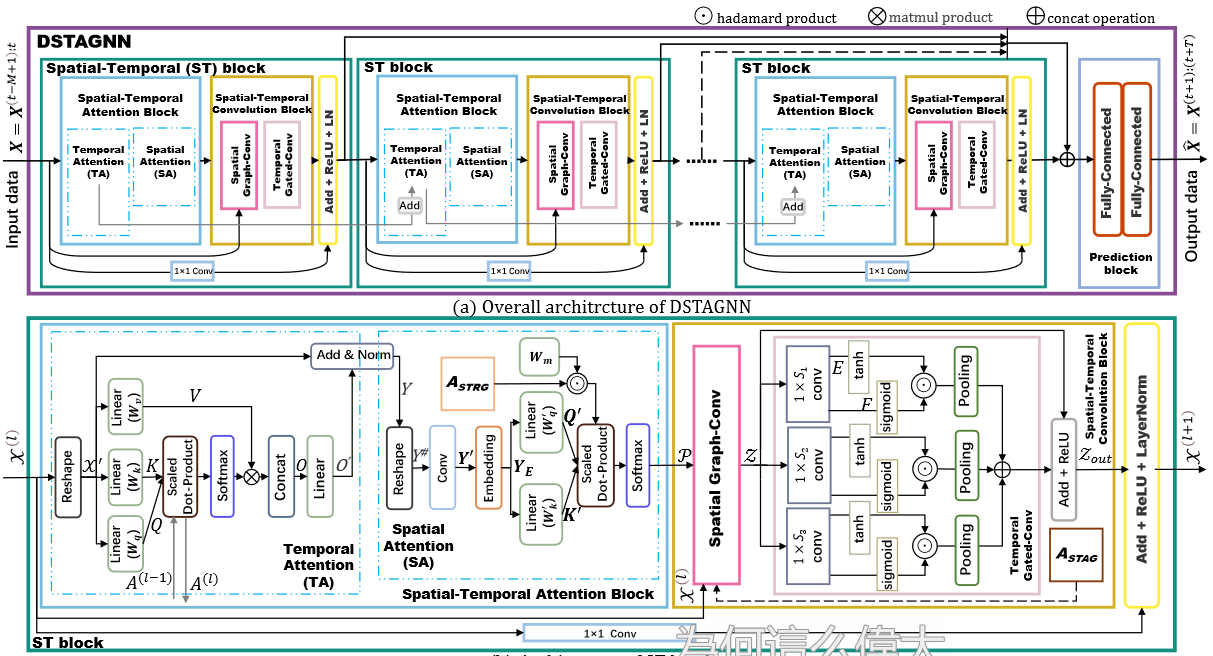
Model

Network Structure

Details

0. 前置知识

节点：$V$
节点数量：$N$
节点间连接（边）：$E$
图：$\mathcal{G}=(V,E)$
邻接矩阵：$A\in {\mathbb{R}}^{N\times N}$
t时刻的图信号：$X^t\in {\mathbb{R}}^{N\times C_p}$，其中$C_p$表示交通参数的类型（如交通流量、速度），本论文只有一个交通参数，即$C_p=1$
数据记录：$X^{(t-M+1):t}\in {\mathbb{R}}^{N\times C_p\times M}$
预测目标：$X^{(t+1):(t+T)}\in {\mathbb{R}}^{N\times C_p\times T}$
模型$\mathcal{F}$：$X^{(t+1):(t+T)}=\mathcal{F}[X^{(t-M+1):t};\mathcal{G}]$

1. 节点特征的表示与转换

Take the traffic flow $X^f\in R^{D\times d_t\times N}$ at the N recording points for D days as an example, where dt is the number of recording times per day (if recordings are taken once every 5 minutes, then $d_t$ = 288).
For each recording point, the oneday traffic data is treated as a vector, then a set of multi-day traffic data is denoted as a vector sequence. For example, the vector sequence obtained at recording point n ($n\in N$) is denoted as $X_n^f=(w_{n1},w_{n2},\cdots ,w_{nD})$, $w_{nd}\in {\mathbb{R}}^{d_t}$, where $d\in [1,D]$.

提取交通流量信息：

$$m_{nd}=\frac{{\Vert {\mathit{w}}_{nd}\Vert }_2}{Z_n},Z_n=\sum _{d=1}^D{\Vert {\mathit{w}}_{nd}\Vert }_2$$

In this way, the vector sequence of the recording point n is transformed into a probability distribution $P_n\{X_d=m_{nd}\}$, and each day has a probability mass $m_{nd}\in [0,1]$ and $\sum _d{m}_{nd}=1$, which denotes the proportion of traffic volume in a certain day over a period of time.

P.S.

• 为什么流量信息是一天的流量占一段时间的比？
• 这里为什么用二范数，而不是直接对一天各个时段的流量进行求和？

2. 时空感知距离与时空关联图

概率分布变换代价（使用Wassertein距离）：
利用余弦距离作为变换代价：

使用Wassertein距离计算两个节点的差异：

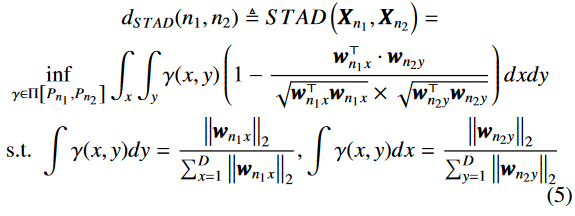
节点间的关联度矩阵${\mathit{A}}_{STAD}\in {\mathbb{R}}^{N\times N}$：

$${\mathit{A}}_{STAD}[i,j]=1-d_{STAD}(i,j)\in [0,1]$$

通过设定稀疏水平$P_{sp}$（超参数），选取每行 $N_r=N\times P_{sp}$ 个节点（关联度最大的几个），其余的设为0，就获得了时空关联图 ${\mathit{A}}_{STRG}\in {\mathbb{R}}^{N\times N}$。
对时空关联图 ${\mathit{A}}_{STRG}$ 进行二值化，获得时空感知图 ${\mathit{A}}_{STAG}$。

P.S.

• 为什么用余弦变换作为代价？
• 为什么用Wassertein距离计算节点的差异（关联）？
• 为什么关联图中只选了 $P_{sp}$ 个节点？

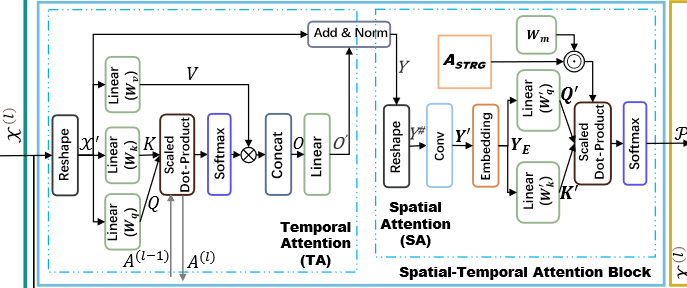
3. 时空注意力块

这里用到了多头注意力机制，参考Attention Is All You Need。

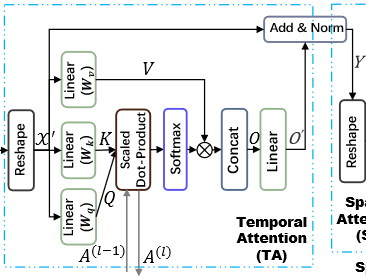
时间注意力

• 这里的 ${\mathcal{X}}^{(l)}\in {\mathbb{R}}^{N\times c^{(l-1)}\times M}$ 是输入，经过reshape，变成 ${\mathcal{X}}^{\prime (l)}\in {\mathbb{R}}^{c^{(l-1)}\times M\times N}$。
• ${\mathcal{X}}^{\prime (l)}{\mathit{W}}_q^{(l)}\triangleq Q^{(l)},{\mathit{X}}^{(l)}{\mathit{W}}_k^{(l)}\triangleq K^{(l)},{\mathit{X}}^{(l)}{\mathit{W}}_v^{(l)}\triangleq V^{(l)}$ Q和K用来计算不同节点之间的相关性（注意力系数），$W_{q,k,v}^{(l)}\in {\mathbb{R}}^{N\times d}$，$Q^{(l)},K^{(l)},V^{(l)}\in {\mathbb{R}}^{c^{(l-1)}\times M\times d}$。
• 注意力*：
  • Scaled Dot-Product（论文Attention Is All You Need里来的。）$A^{(l)}=\frac{Q^{(l)}{K}^{(l{)}^{\mathrm{\top }}}}{\sqrt{d_h}}+A^{(l-1)}$
  • 注意力：$\mathrm{Att}(Q^{(l)},K^{(l)},V^{(l)})=\mathrm{Softmax}\left(A^{(l)}\right)V^{(l)}$
• 多头注意力机制（论文Attention Is All You Need里来的。）$O^{(h)}=\mathrm{Att}(Q{\mathit{W}}_q^{(h)},K{\mathit{W}}_k^{(h)},V{\mathit{W}}_v^{(h)})$ 其中 ${\mathit{W}}_{q,k,v}^{(h)}\in {\mathbb{R}}^{d\times d_h}(d_h=d/H)$。
• Concat：$O=[O^{(1)},O^{(2)},\dots ,O^{(H)}]$ 经过Reshape，获得 $\mathit{O}\in {\mathbb{R}}^{c^{(l-1)}\times M\times H\times d_h}$。
• Linear层把输出的大小还原，获得 $O^{\prime }\in {\mathbb{R}}^{c^{(l-1)}\times M\times N}$。
• 带残差的LayerNorm：$Y=\mathrm{LayerNorm}(\mathrm{Linear}(\mathrm{Reshape}(O))+X^{\prime })$ 输出 $Y\in {\mathbb{R}}^{c^{(l-1)}\times M\times N}$。
  P.S.
• 原文中的LayerNorm公式错了。
• $d$ 和 $d_h$是如何决定的？
• Scaled Dot-product 为什么用残差？

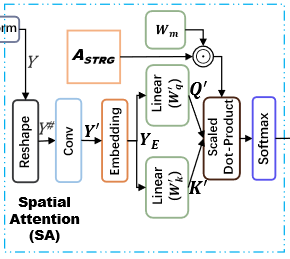
空间注意力

• Reshape：$Y\in {\mathbb{R}}^{c^{(l-1)}\times M\times N}$ 转换成 $Y^{\mathrm{\#}}\in {\mathbb{R}}^{c^{(l-1)}\times N\times M}$。
• Conv：
  • 先把 $Y^{\mathrm{\#}}\in {\mathbb{R}}^{c^{(l-1)}\times N\times M}$ 中的时间维度 $M$ 映射到 $d_E$ 维的高维空间。（怎么映射？为什么要映射？）
  • 对特征维 $c^{(l-1)}$ 做一维卷积，获得二维矩阵$Y^{\prime }\in {\mathbb{R}}^{N\times d_E}$。（卷积核大小是 $c^{(l-1)}$？）
  • Embedding：

    Then, we add positional information to $Y^{\prime }$ through an embedding layer to get $Y_E$.

• 注意力机制（这里的空间注意力其实只算了注意力中的相关性，在下一步卷积中使用）：

  Instead of using the self-attention fully generated from $Y_E$ as in conventional transformers, here we introduce the temporal-spatial relevance graph $A_{STRG}$ with learned correlation between nodes to amend the attention in the SA module. Thus the improved spatial attention with H heads is denoted as: $\begin{array}{c}{\mathit{P}}^{(h)}=\mathrm{Softmax}(\frac{{\left({\mathit{Y}}_E{\mathit{W}}_k^{\prime (h)}\right)}^{\mathrm{\top }}\left({\mathit{Y}}_E{\mathit{W}}_q^{\prime (h)}\right)}{\sqrt{d_h}}+{\mathit{W}}_m^{(h)}\odot {\mathit{A}}_{STRG})\\ \mathcal{P}=[{\mathit{P}}^{(1)},{\mathit{P}}^{(2)},\dots ,{\mathit{P}}^{(H)}]\end{array}$ where ${\mathit{W}}_k^{\prime (h)},{\mathit{W}}_q^{\prime (h)}\in {\mathbb{R}}^{d_E\times d_h},{\mathit{W}}_m^{(h)}\in {\mathbb{R}}^{N\times N}$ are learnable parameters, $\odot$ is the element-wise Hadamard product, ${\mathit{W}}_m^{(h)}$ is used to amend ${\mathit{A}}_{STRG}$ for adjusting the attention of each head ${\mathit{P}}^{(h)}\in {\mathbb{R}}^{N\times N}$, and the output $\mathcal{P}\in {\mathbb{R}}^{H\times N\times N}$ denotes the dynamic spatial-temporal attention tensor by combining the outputs from each head.

P.S.

• Conv中的高维映射怎么映射？为什么要映射？
• Conv中的一维卷积怎么把整个 $c^{(l-1)}$ 卷没了？
• 这里为什么不用残差了，而是用 $A_{STRG}$？

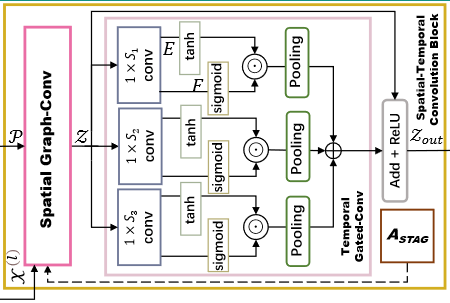
4. Spatial-Temporal Convolution Block

空间图卷积

这里使用了ChebyNet卷积，待深入。

$$g_{\theta }\ast Gx=g_{\theta }(\mathit{L})x=\sum _{k=0}^{K-1}{\mathit{\theta }}_k(T_k(\tilde{\mathit{L}})\odot {\mathit{P}}^{(k)})x$$

图信号：$x={\mathit{x}}_{\mathit{t}}\in {\mathbb{R}}^N$
归一化的拉普拉斯矩阵：$\tilde{\mathit{L}}=\frac{2}{{\lambda }_{max}}(\mathit{D}-{\mathit{A}}^{\ast })-{\mathit{I}}_N$
邻接矩阵：${\mathit{A}}^{\ast }={\mathit{A}}_{STAG}$
参数：$\mathit{\theta }\in {\mathbb{R}}^K$
第k个头的空间-时间注意力矩阵：${\mathit{P}}^{(k)}\in {\mathbb{R}}^{N\times N}$

P.S.

• 为什么把P直接哈达玛乘在切比雪夫多项式上？

时间门控卷积（Temporal gated convolution）

论文提出了M-GTU (Multi-scale Gated Tanh Unit) 卷积模块捕捉交通流数据中的动态时间信息。

M-GTU由三个GTU模块组成，每个GTU由Convolution和Gating两步组成。

• 卷积：
  • 输入：${\mathcal{Z}}^{(l)}\in {\mathbb{R}}^{N\times M\times C^{(l)}}$。
  • 卷积核：$\mathrm{\Gamma }\in {\mathbb{R}}^{1\times S\times c^{(l)\times 2c^{(l)}}}$，其中，$c^{(l)}$ 是输入的通道数（节点的特征数），$2c^{(l)}$ 是输出的通道数，卷积核的大小是 $1\times S$，1是节点个数维度上的大小，S是时间维度上的大小。
  • 卷积公式：${\mathcal{Z}}^{\prime (l)}=\mathrm{\Gamma }\ast {\mathcal{Z}}^{(l)}\in {\mathbb{R}}^{N\times (M-(S-1))\times 2C^{(l)}}$
• Gating：把 ${\mathcal{Z}}^{\prime (l)}$ 沿着通道维度等分成两份 $E$ 和 $F$，则输出为 $\varphi (E)\odot \sigma (F)\in {\mathbb{R}}^{N\times (M-(S-1))\times 2C^{(l)}}$
• Concat：虽然图上有Pooling，但是代码中并没有，使用三个不同的卷积核 $S_1,S_2,S_3$ 卷积后，将三个输出沿着时间轴拼接。
• Linear：将Concat的结果放进Linear层，恢复原来的大小。

self.fcmy = nn.Sequential(
    nn.Linear(3 * num_of_timesteps - 12, num_of_timesteps),
    nn.Dropout(0.05),
)

P.S.

• 为什么要用GTU？

Datasets

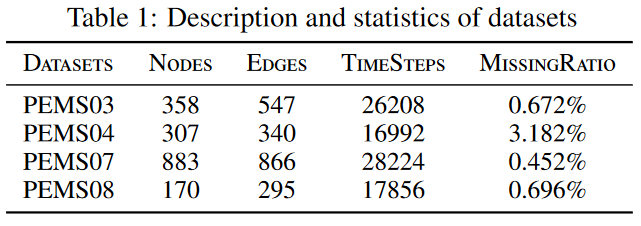
文章使用了PEMS03、PEMS04、PEMS07、PEMS08三个数据集。