1 2 7 9 波泼墨佛的特呢了
常量因子和算法复杂度：
对于算法的时间和空间性质，最重要的是其量级和趋势，这些是算法代价的主要部分，而代价函数的常量因此可以忽略不计。例如，可以认为3n²和100n²属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就可以认为它们的代价“差不多”。基于这样的考虑，人们提出描述算法性质的“大O记法”。
大O记法的严格定义：对于单调的整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有f(n)<=c·g(n)，就说函数g是f的渐进函数(忽略常量因子)，记为f(n)=O(g(n))。易见，f(n)=O(g(n))说明在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束。把上述描述方式应用于算法的代价问题。假设存在函数g，使得算法A处理规模为n的问题实例所用的时间T(n)=O(g(n))，则称O(g(n))为算法A的渐进时间复杂度，简称时间复杂度。算法的空间复杂度S(n)的定义与此类似。
关于大O记法的几点说明。
首先，如果T(n)=O(g(n))，那么对于任何增长速度比g(n)更快的函数g'(n)，显然也有T(n)=O(g'(n))。这说明上述定义考虑的是算法复杂度的上限(应该说的是描述的是最糟糕的情况)。
其次，虽然可以选择任意合适的函数作为描述复杂性时使用的g(n)，但一组简单的单调函数已足以反映人们对基本算法复杂度的关注。(尽量简单)。在算法和数据结构领域，人们最常用的是一下这组渐进复杂度函数：
O(1)，常量复杂度
O(logn)，对数复杂度
O(n)，线性复杂度
O(n·logn)，
O(n²)，
O(n³)，
O(2ⁿ)，指数复杂度
在考虑量级时对数的底不是主要因素(可能差一个常量因子)，因此可以忽略。
按照上面的理论，如果算法的改进只是加快了常量倍，也就是说减少了复杂性函数中的常量因子，算法的复杂度没有变化。但是，在许多实际情况中，这种改进是有意义的。例如，需要3天时间算出明天的天气预报，与只需半天就能算出，算法的实际价值是截然不同的。
算法复杂度的意义
算法复杂度反过来决定了算法的可用性。
解决同一问题的不同算法
以斐波那契数列为例，定义如下：
F0=F1=1
Fn = Fn-1 + Fn-2，对于n>1
1 # 斐波那契数列，递归法 2 def fib(n): 3 if n <= 1: 4 return 1 5 return fib(n-1) + fib(n-2) 6 7 print(fib(18)) # 4181
把参数n看作问题实例的规模，不难看出，计算Fn的时间代价(考虑求加法操作的次数)大致等于Fn-1 和 Fn-2的代价之和。这一情况说明，计算Fn的时间代价大致等于斐波那契数Fn的值。根据已有结论：
括号里的表达式大约等于1.618，所以计算Fn的时间代价按n值呈指数增长。对于较大的n，这一计算就需要很长很长时间。
使用递推方法，
1 def fib(n): 2 if n <= 1: 3 return 1 4 a = b = 1 5 for i in range(1, n): # n=2时只进行一次计算... 6 c = b 7 b = a + b 8 a = c 9 return b 10 11 print(fib(18)) # 4181
书上是这么写的，
1 def fib(n): 2 f1 = f2 = 1 3 for i in range(1, n): # n=2时只进行一次计算...，0、1对于range无效，所有可以把n=0或1的情况合并 4 f1, f2 = f2, f1+f2 5 return f2 6 7 print(fib(18)) # 4181
使用这个算法计算Fn的值，循环前的工作只做一次，循环需要做n-1次。基本操作执行次数与n值呈某种线性关系。
这一例子说明，解决同一问题的不同算法，其计算复杂大的差异可以很大，甚至截然不同。当然，在实际工作中，可能两个算法可有所长，例如一个时间复杂大较低但空间复杂度较高，而另一个情况正好相反，这时，就需要做进一步的细致分析。
1.3.3 算法分析
算法分析的目的是推导出算法的复杂度，其中最主要的技术是构造和求解递归方程。
基本循环程序
这里只考虑时间复杂度，考虑最基本的循环程序，其中只有顺序组合、条件分支和循环结构。分析这种算法只需要几条基本计算规则：
0. 基本操作，认为其时间复杂度为O(1)。如果是函数调用，应该将其时间复杂度代入，参与整体时间复杂度的计算。
1. 加法规则(顺序复合)。如果算法(或所考虑算法片段)是两个部分(或多个部分)的顺序组合，其复杂性是这两部分(或多部分)的复杂性之和。以两个部分为例：
1
其中T1(n)和T2(n)分别为顺序复合的两个部分的时间复杂度。由于忽略了常量因子，加法等价于求最大值，取T1(n)和T2(n)中复杂度最高的一个。
2. 乘法规则(循环结构)。如果算法(或所考虑的算法片段)是一个循环，循环体将执行T1(n)次，每次执行需要T2(n)时间，那么：
1
3. 取最大规则(分支结构)。同顺序复合。如果算法(或所考虑的算法片段)是条件分支，两个分支的时间复杂性分别为T1(n)和T2(n)，则有：
实例，
1 for i in range(n): # m1的每行 2 for j in range(n): # 笛卡儿积，倒数第二层是m1的一行，m2的每列 3 x = 0.0 4 for k in range(n): # 最里层是m1的行和m2的列一一对应 5 x += m1[i][k] + m2[k][j] 6 m[i][j] = x
这个程序片段是一个两重循环(前两行)，循环体是一个顺序语句(3~6行)，其中还有一个内嵌的循环。根据上面的复杂性计算规则，可以做如下推导：
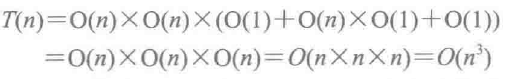
另一个实例，
求n阶方形矩阵的行列式。考虑两种不同算法。
行列式回忆，https://blog.csdn.net/zhaoruixiang1111/article/details/79185927
高斯消元法：通过逐行消元，把原矩阵变换成一个上三角线矩阵最后乘起所有对角线元素，就得到矩阵行列式的值。
先不看了。。
递归算法的复杂度
1 def recur(n): 2 if n == 0: 3 return g(...) 4 somework 5 for i in range(a): 6 x = recur(n/b) 7 somework 8 somework
n为0时直接返回结果，否则原问题将归结为a个规模为n/b的子问题，其中a和b是由具体问题决定的两个常量。另外，在本层递归中还需要做一些工作(用somework表示)，其时间复杂度可能与n有关，设为O(nk)。k也应该为常量，k=0时表示这部分工作与n无关。这样就得到了下面的递归方程：
有如下结论：
1.3.4 python程序的计算代价(复杂度)
时间开销
在考虑python程序的时间开销时，有一个问题特别需要注意：python程序中的许多基本操作不是常量时间的。
下面是一些基本情况：
基本算术运算是常量时间操作，逻辑运算是常量时间操作。
组合对象的操作有些常量时间的，有些不是。例如：
复制和切片通常需要线性时间(与长度有关，是O(n)时间操作)。
list和tuple的元素访问和元素赋值，是常量时间。
dict操作比较复杂，第8章有详细讨论。
使用组合对象的程序，需要特别考虑其中操作的复杂度。
字符串也应该看作组合对象，其许多操作不是常量时间的。
创建对象也需要付出空间和时间，空间和时间代价都与对象大小有关。对于组合对象，这里可能有需要构造的一个个元素，元素有大小问题，整体看还有元素个数问题。通常应看作线性时间和线性空间操作(以元素个数作为规模)。
python结构和操作的效率问题，(更详细的在后面)
构造新结构，如构造新的list、set等。构造新的空结构(空表、空集合等)是常量时间操作，而构造一个包含n个元素的结构，则至少需要O(n)时间。统计表明，分配长度为n个元素的存储快的时间代价为O(n)。
一些list操作的效率：元素访问和元素修改是常量操作，但一般的插入 / 删除元素操作(即使只加入一个元素)都是O(n)时间操作。
字典操作的效率：主要操作是插入新的键值对和根据键查找值。它们的最坏情况复杂度为O(n)，但平均复杂度为O(1)。最坏情况是啥？？
上面复杂度中的n都是有关结构中的元素个数。程序里经常用到这些操作，它们的效率对程序效率有重大影响。另外，有些操作的效率高。例如，在列表最后追加和删除元素的操作效率高，在其他地方插入和删除元素的效率低，应该优先选用前者。
空间开销
在程序里使用任何类型的对象，都需要付出空间的代价。建立一个列表或元组，至少要占用元素个数那么多空间。如果一个表的元素个数与问题规模线性相关，建立它的空间付出至少为O(n)(如果元素也是新创建的，还需考虑元素本身的存储开销)。
相对而言，列表和元组是比较简单的数据结构。集合和字典需要支持快速查询等操作，其结构更加复杂。包含n个元素的集合或字典，至少需要占用O(n)的存储空间。
这里还有两个问题需要注意：
1) python的各种组合数据对象都没有预设最大元素个数。在实际使用中，这些结构能根据元素个数的增长自动扩充存储空间。从空间占用角度看，其实际开销在存续期间可能变大，但通常不会自动缩小(即使后来元素变少了)。
2) python自动存储管理系统的影响。例如，如果在程序里创建了一个列表，此后一直将其作为某个全局变量的值，这个对象就会始终存在并占用存储空间。如果将其作为某个函数里局部变量的值，或者虽然作为全局变量的值，但后来通过赋值将其抛弃，那么这个列表对象就可以被回收。
总之，在估计python程序的空间开销时，上面这些细节也需要考虑。
python语言提供了很多高级结构，使人很容易通过简短的程序来完成很多工作，例如很容易构造出新的列表或元组。但是这种方便性有时会带来负面作用。
python程序的时间复杂度实例
假设需要把得到的一系列数据存入一个列表，其中得到一个数据是O(1)常量时间操作。代码如下：
1 # 方式一： 2 data = [] 3 while 还有数据: 4 x = 下一个数据 5 data.insert(0, x) 6 7 # 方式二： 8 data = [] 9 while 还有数据: 10 x = 下一个数据 11 data.insert(len(data), x) # 或data.append(x) # 问题是求长度的操作时间复杂度是多少？？
方式一为O(n²)，方式二为O(n)。第3章将介绍列表的实现方式。
另一个例子，
1 import time 2 3 def test1(n): 4 lst = [] 5 for i in range(n*100000): 6 lst = lst + [i] # 定义变量i, 创建列表[i], 把[i]加到大列表 7 return lst 8 9 def test2(n): 10 lst = [] 11 for i in range(n*100000): 12 lst.append(i) # 定义变量i, 把i追加到大列表 13 return lst 14 15 def test3(n): 16 return [i for i in range(n*100000)] 17 18 def test4(n): 19 return list(range(n*100000)) 20 21 t1 = time.time() 22 test4(1) 23 print(time.time() - t1) 24 25 # 10000时 26 # 0.10614371299743652 0.45339322090148926 2.323219060897827 27 # 0.0009737014770507812 0.0014874935150146484 0.0029752254486083984 28 # 0.0004966259002685547 0.0010044574737548828 0.0019838809967041016 29 # 0.0004961490631103516 0.0004961490631103516 0.005434751510620117 0.0009915828704833984 30 31 # 100000时 32 # 16.377396821975708 0.014342546463012695 0.005952358245849609 0.df 003473043441772461
从上面的四种方法可以看出，速度越来越快。
程序实现和效率陷阱
设计一个算法，通过对它的分析可能得到抽象算法的时间与空间复杂度。进而，采用某个编程语言可以做出该算法的实现。这样就出现一个问题：算法实现的时间开销与原算法的时间复杂度之间有什么关系？理想的情况应该是相应程序的时间开销增长趋势应该达到原算法的时间复杂度。但是，如果实现做得不好，假设原算法的时间复杂度为O(n)，其实现程序也可能比这差，例如达到O(n²)或者更差。因此在考虑程序的开发时，不但要选择好的算法，还要考虑如何做出算法的良好实现。
应该特别指出，用python等高级语言编写程序存在一些“效率陷阱”，这种陷阱可能使原本可以用计算机做的事情变得不可行(时间代价太大)，或者至少也浪费了计算机和人的大量时间。最常见的错误做法就是毫无意义地构造一些可能很大的复杂结构。例如在递归定义的函数里的递归调用中构造复杂的结构，而后只使用了其中的个别元素。从局部看，这样做使得常量时间的操作变成了线性时间操作。但从递归算法的全局看，这样做法经常会使多项式时间(也就是乘法)算法变成指数时间算法，也就是说，把原来有用的算法变成了基本无用的算法。
这种事例也说明了一个情况：python这样的编程系统提供了许多非常有用的高级功能，但是要想有效地使用它们，有必要了解数据结构的一些深入情况。
1.4 数据结构
1.4.2 计算机内存对象表示
内存单元和地址
内存的基本结构是线性排列的一批存储单元。每个单元的大小相同，可以保存一个单位大小的数据。具体单元大小可能因计算机的不同而有所不同。在目前最常见的计算机中，一个单元可以保存一个字节(8位二进制)的数据。因此存放一个整数或浮点数，需要连续的几个单元。例如标准的浮点数需要8个单元。需要8个？？
内存单元的唯一编号，称为单元地址，简称地址。在程序执行中，对内存单元的访问都通过地址进行。在许多计算机中，一次内存访问可以存取若干单元的内容。例如目前常见的64位计算机，一次可以存取8个字节的数据，也就是说一次操作访问8个单元的内容。基于地址访问内存单元是一个O(1)操作，与单元的位置或整个内存的大小无关，这是分析与数据结构有关的算法时的一个基本假设(满足这种假设的存储器称为随机访问存储器RAM，与顺序访问的磁盘、磁带相对应)。在高级语言层面讨论和分析数据结构问题时，人们通常不关心具体的单元大小或地址范围，只假定所考虑数据保存在内存的某处，而且假定这种访问是常量时间的。
对象存储和管理
标识对象最简单的方式就是直接使用对象的内存地址，而且这是唯一标识。
对象的访问
在编程语言层面，知道了一个对象的标识就可以直接访问它。已知对象标识(无论它是否直接为对象地址)，访问相应对象的操作可以直接映射到已知地址来访问内存单元，这种操作是O(1)时间操作。
如果被访问的是一个组合对象，其中包含了一组元素，这些元素被安排在一块内存区域(一块连续的元素存储区)里，而且每个元素的存储量相同。这种情况下，可以给每个元素一个顺序编号(通常称为下标，index)。如果知道了该组合对象的存储区位置，又知道要访问的元素的编号，访问元素也是O(1)时间操作。loc(k) = p + k * a
对象关联的表示
下面的先不看了。。。
第2章 抽象数据类型和python类
2.1 抽象数据类型
2.1.1 数据类型和数据构造
基本数据类型：bool、int、float、str
组合数据类型：list、tuple、set、dict
补充，
有理数：一个整数和一个正整数的比。0也是有理数。有理数是整数和分数的集合，整数可以看成分母为1的分数。有理数的小数部分是有限的或无限循环的。无限不循环的是无理数。
7.1.1 定义和图示
一个图是一个二元组G = (V, E)，其中：
V是顶点集合。
E是边的集合。
V中的顶点也称为图G的顶点，E中的边也称为图G的边。
有向图用尖括号表示，无向图用圆括号表示。
如果在图G里有边<vi , vj>属于E，则称顶点vj 是vi 的邻接结点或邻接点。有向图里的邻接关系是单向的，无向图里的邻接关系是双向的。
图和图示
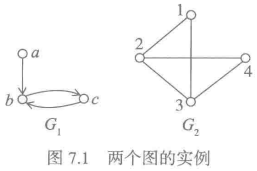
不关心顶点的位置、顶点之间的距离、不同边之间的交叉，只关心存在哪些顶点、顶点之间的邻接关系。
7.1.2 图的一些概念和性质
完全图：任意两个顶点之间都有边的图。显然：
1）n个顶点的无向完全图有n*(n-1)/2条边。
2）n个顶点的有向完全图有n*(n-1)条边。
对于不同的图，其中边的条数可能达到顶点个数的平方，但也可能很少。这个事实在考虑与图有关的算法的时间和空间复杂度时经常用到。
度：一个顶点的度就是与它邻接的边的条数。对于有向图，顶点的度分为入度和出度。
性质7.1 (顶点数、边数和顶点度数的关系) 无论对于有向图还是无向图，顶点数n、边数e、顶点度数满足下面关系：
路径和相关性质
1）路径的长度就是该路径上边的条数。
2）回路(回环)指起点和终点相同的路径。
3）如果一个环路，除起点和终点外的其他顶点均不相同，则称为简单回路。
4）简单回路是内部不包含回路的路径。简单回路也是简单路径。
如果vi 到vj 存在非简单路径(即包含回环的路径)，那么从vi 到vj 就有无穷多条不同的路径，路径之间的不同在于在环路上绕圈次数的不同。
有根图：如果G中存在一个顶点v，从v到图中其他顶点均有路径，则称G为有根图，v为G的一个根。根可以不止一个。
连图图
连通：如果在无向图G中存在从vi 到vj 的路径，则说从vi 到vj 连通。默认任一顶点vi 到于其自身相通。对有向图，连通性也可以类似地定义，但连通性不是双向的。
连通无向图：如果无向图G中任意两个顶点之间都连通，则称G为连通无向图。
强连通有向图：如果有向图G中任意两个顶点vi 和vj 双连通(从vi 到vj 连通并且从vj 到从vi 也连通)，则称G为强连通有向图。
显然，完全无向图都是连通图，完全有向图都是强连通有向图。但反过来不对，存在非完全的连通无向图和强连通的有向图。(是否完全是说有边，连通是说有路径，进一步说，有边一定有路径，有路径不一定有边)
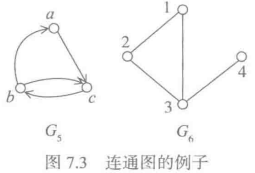
例7.4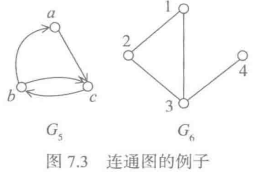 
G5是强连通有向图，G6是连通无向图。但它们都不是完全图。
性质7.2 (最小连通无向图的边数) 包含n个顶点的最小连通无向图G恰好有n-1条边。(无向树)
最小连通图，即去掉任一条边都不再是连通图。
性质7.3 (最小有根图的边数) 包含n个顶点的最小有根图G恰好有n-1条边。 (有向树)
最小有根图，即去掉任一条边都不再是有根图。
从某种角度看，树可看作图的一个子类。满足性质7.2的图称为无向树。无向树中的任何一个顶点都可以看作树的根，从它出发可以到达任何其他顶点。满足性质7.3的有向图称为有向树，这个有向树的根可以看作树根，树中存在从树根到其他每个顶点的路径。
子图、连通子图
例7.5 下面给出了G1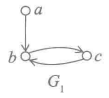
的几个子图：
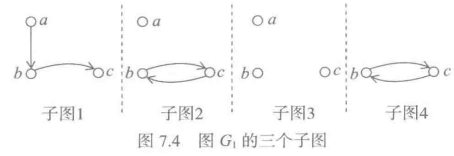
一个图可能不是连通图(或强连通图)，但它的一些子图可能是连通图(或强连通图)，这种子图称为原图的连通子图(或强连通子图)。
图G的一个极大连通子图(连通分量)G’是图G的一个连通子图，而且G中不存在真包含G’的连通子图(G’就是一个最大的连通子图)。如果G本身连通，它将只有一个连通分量，就是它本身。如果G不连通，则其连通分量多于一个。
不难看出，无向图G的所有连通分量形成了图G的一个划分，每个连通分量包含图G的一集顶点和它们之间的所有边，而这些顶点集和边集的并集就是原来的G。
与上面定义类似，有向图G的一个极大强连通子图称为它的一个强连通分量。不同的是，图G的强连通分量只形成其顶点的一个划分，所有强连通分量的并集未必等于图G，可能少一些连接不同强连接分量的有向边。
带权图和网络
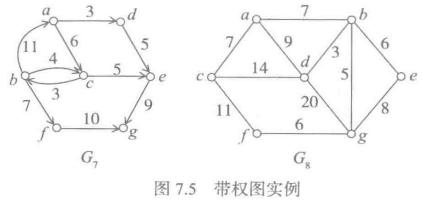
如果图G中的每条边都被赋予一个权值，则称G为带权图(带权有向图和带权无向图)。带权的连通无向图也被称为网络。
7.1.3 图抽象数据类型
7.1.4 图的表示和实现
邻接矩阵
邻接矩阵是表示图中顶点间邻接关系的方阵。对于n个顶点的图G=(V, E)，其邻接矩阵是一个n*n的方阵。图中每个顶点(按顺序)对应于矩阵里的一行和一列，矩阵元素表示图中的邻接关系。
最简单的邻接矩阵是以0/1为元素值的方阵。
对于带权图，其邻接矩阵元素的定义是
的邻接矩阵为
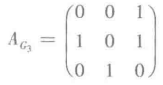和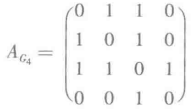
易见，
无向图的邻接矩阵都是对称矩阵，因为其邻接关系是对称的。
由于没有考虑顶点到自身的边，所以矩阵对角线上的元素都是0。如果希望用矩阵表示图中的连通关系，就应该令矩阵的对角线元素为1，因为默认各顶点到自身连通。
行对应出边，列对应入边，行/列中非零元素的个数对应于顶点的出度/入度。
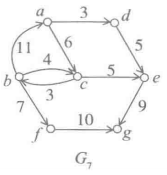对应
邻接矩阵表示法的缺点
图的邻接表表示
邻接表就是为图中每个顶点关联一个边表，其中记录这个顶点的所有邻接边。
顶点是图中最基本的成分，通常有标识，也可以顺序编号，以便可以通过编号随机访问。而边是图中的附属部件，经常需要访问一个顶点的各条边。另一方面，图中顶点通常不变，而边增减的情况较多。由于这些情况，实际中经常使用一个顺序表表示图中顶点，每个顶点关联一个表示其邻接边表的链表。在对应顶点的边表里，每个表结点对应一条边，结点里记录该边终点的下标。边表长度就是该顶点的出度。
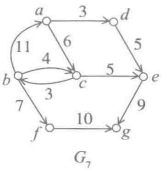对应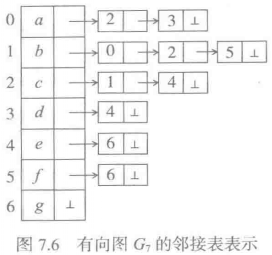
图7.6里顶点信息只有其标记，可以根据实际需要增加更多数据域，存储所需的任何信息。例如要表示边的权值，就需要在每个链表结点里增加相应的域。
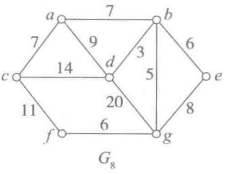对应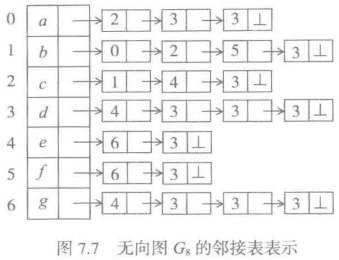
同一条边应该出现在两个邻接点的边表里，所有链接表的结点数等于边数的二倍。
7.2 图结构的python实现
1）两层list或两层tuple作为邻接矩阵的直接实现来表示图结构。这种方法结构简单，使用方便，容易判断顶点的邻接关系。但存储代价较大，不适合特别大的图。
2）利用字典，以两个顶点的下标对(i，j)为🗡，实现从顶点对到邻接关系的映射。这种方法检索效率很高，采用适当的技术，可以做到图的空间开销与图中边数成正比，适合表示稀疏矩阵。
3）利用python内置的bytearray或标准库array类型。bytearray是内置类型，与str类似，但为可变类型，bytearray对象的元素是二进制字节，可以用于表示边的存在与否，存储效率较高。array是标准库里定义的数值汇集类型，其对象的元素可以是整数或浮点数等基本类型的值，可用于表示带权图。
4）自定义类型实现邻接表表示，其中具体数据的组织可以考虑上述各种技术。
下面是两种自定义的实现方法。
7.2.1 邻接矩阵实现
1 class Graph: 2 def __init__(self, mat, unconn=0): 3 ''' 4 :param mat: 二维，提供图的基本架构，主要是确定图的顶点个数。 5 :param unconn: 为无关联提供的一个特殊值， 6 ''' 7 vnum = len(mat) 8 for x in mat: 9 if len(x) != vnum: # 检查是否为方阵 10 raise ValueError('error') 11 self._mat = [mat[i][:] for i in range(vnum)] # 做拷贝 12 self._unconn = unconn 13 self._vnum = vnum 14 15 # 顶点个数 16 def vertex_num(self): 17 return self._vnum 18 19 def _invalid(self, v): # 判断下标是否合法 20 return v < 0 or v >= self._vnum 21 22 def add_vertex(self): 23 ''' 24 不仅需要给矩阵增加一行，还要为每行增加一个元素 25 ''' 26 pass 27 28 # 顶点vi到顶点vj的边 29 def add_edge(self, vi, vj, val=1): 30 if self._invalid(vi) or self._invalid(vj): 31 raise GraphError('not a valid vertex') 32 self._mat[vi][vj] = val 33 34 def get_edge(self, vi, vj): 35 if self._invalid(vi) or self._invalid(vj): 36 raise GraphError('not a valid vertex') 37 return self._mat[vi][vj] 38 39 # 顶点vi的出边，获得每行有边的结点列表 40 def out_edges(self, vi): 41 if self._invalid(vi): 42 raise GraphError('not a valid vertex') 43 return self._out_edges(self._mat[vi], self._unconn) # 一行数据 44 45 @staticmethod 46 def _out_edges(row, unconn): 47 edges = [] 48 for i in range(len(row)): 49 if row[i] != unconn: 50 edges.append((i, row[i])) # 二元组分别为边的终点和便信息(对于带权图就是权值) 51 return edges 52 53 # python规定，对一种类型的对象作用内置函数strs时，去调用该类的__str__方法。 54 def __str__(self): 55 return '[\n' + ',\n'.join(map(str, self._mat)) + '\n]' + '\nUnconnected: ' + str(self._unconn)
7.2.2 邻接表实现
邻接矩阵的缺点是空间占用与顶点数的平方成正比，可能带来很大的浪费。另外，邻接矩阵不容易增加顶点，不太适合以逐步扩充的方式构造图对象。
1 class GraphAL(Graph): 2 def __init__(self, mat=[], unconn=0): # 为mat设置默认值，以支持从空图出发逐步构造图对象 3 vnum = len(mat) 4 for x in mat: 5 if len(x) != vnum: 6 raise ValueError('error') 7 self._mat = [Graph._out_edges(mat[i], unconn) for i in range(vnum)] # 主要是这一行不一样 8 self._vnum = vnum 9 self._unconn = unconn 10 11 def add_vertex(self): 12 self._mat.append([]) # 给已有的图添加顶点，只需在外层表中增加一个表示新顶点的项，对应的边表设置为空表。 13 self._vnum += 1 14 return self._vnum - 1 15 16 # 与邻接矩阵不同的是，邻接表里的边表已经排除无边，所以加边操作就有点复杂了 17 def add_edge(self, vi, vj, val=1): 18 if self._vnum == 0: 19 raise GraphError('empty graph') 20 if self._invalid(vi) or self._invalid(vj): 21 raise GraphError('not a valid vertex') 22 row = self._mat[vi] # 列表元素为(i, w) 23 i = 0 24 while i < len(row): 25 if row[i][0] == vj: 26 # row[i] = (vj, val) 27 return 28 if row[i][0] > vj: 29 break 30 i += 1 31 self._mat[vi].insert(i, (vj, val)) 32 33 # 有边就能找到，无边就找不到 34 def get_edge(self, vi, vj): 35 if self._invalid(vi) or self._invalid(vj): 36 raise GraphError('not a valid vertex') 37 for r, q in self._mat[vi]: 38 if vj == r: 39 return q 40 return self._unconn 41 42 def out_edges(self, vi): 43 if self._invalid(vi): 44 raise GraphError('not a valid vertex') 45 return self._mat[vi] 46 47 # 构造有向图G7 48 g = GraphAL() 49 for _ in range(7): 50 g.add_vertex() 51 g.add_edge(0, 2, 6) 52 g.add_edge(0, 3, 3) 53 g.add_edge(1, 0, 11) 54 g.add_edge(1, 2, 4) 55 g.add_edge(1, 5, 7) 56 g.add_edge(2, 1, 3) 57 g.add_edge(2, 4, 5) 58 g.add_edge(3, 4, 5) 59 g.add_edge(4, 6, 9) 60 g.add_edge(5, 6, 10) 61 62 print(g._mat) 63 # [ 64 # [(2, 6), (3, 3)], 65 # [(0, 11), (2, 4), (5, 7)], 66 # [(1, 3), (4, 5)], 67 # [(4, 5)], 68 # [(6, 9)], 69 # [(6, 10)], 70 # [] 71 # ]
7.3 基本图算法
7.3.1 图的遍历
深度优先搜索：
首先访问顶点v，并将其标记为已访问。
检查v的邻接顶点，从中选一个尚未访问的顶点，从它出发继续进行深度优先搜索(递归)。不存在这种邻接顶点时回溯(边表里的其他顶点)。
反复上述操作直到从v出发可达的所有顶点都已访问。
如果图中还有未访问的顶点，则选出一个未访问顶点，由它出发重复上述过程，直到图中所有顶点都已访问为止。
通过深度优先遍历顺序得到的顶点序列称为该图的深度优先搜索序列(Depth-First Search)，简称DFS序列。显然，对图中任一顶点的邻接点采用不同的访问顺序，就可能得到不同的DFS序列。如果规定了图中各顶点的邻接点顺序，就确定了DFS序列。
宽度优先遍历：
先访问顶点vi 并将其标记为已访问。
依次访问vi 的所有相邻顶点
(可能规定某种顺序)，再依次访问与
邻接的所有尚未访问的顶点，如此进行下去直到所有可达顶点都已访问。
如果图中还存在未访问的顶点，则选择一个未访问顶点，由它出发按同样方式搜索，直到所有顶点都已访问为止。
通过宽度优先遍历得到的顶点序列称为该图的宽度优先搜索序列(Breadth-First Search)，简称BFS序列。如果规定了图中各顶点的邻接点顺序，就确定了DFS序列。
例7.9 DFS序列：a c b f g e d
BFS序列：a b c d e g f
深度优先遍历的非递归算法
。。。
7.3.2 生成树
本小节讨论的是连通无向图和有向有根图。
性质7.4 (图中路径与路径上的边数) 如果图G有n个顶点，必然可找到一个包含n-1条边的边集合，这个集合里包含了从v0到其他所有顶点的路径。
图G中满足上述性质的n-1条边(加上所有顶点)形成了图G的一个子图T。由于T包含n个顶点且只有n-1条边，因此不可能包含任何回路，形成了一棵树(有向或无向的数)，称T为G的一个生成树。
对无向图G，满足上述性质的子图T是G的一个最小连图子图(去掉其中任一一条边后将不再连通)。
对有根有向图G，满足上述性质的子图T是G的一个最小的有根图(以v0为根)。
如果一个图有生成树，其生成树也可能不唯一。
性质7.5 (生成树的边数) n个顶点的连通图G的生成树恰好包含n-1条边。无向图G的生成树就是G的一个最小连通子图，是一个无环图。有向图的生成树中所有边都位于从根到其他顶点的路径上。
一般而言，一个无向图G(就是一般的图)可能非连通。但由于任何无向图都可以划分为一组连通分量，因此每个无向图都存在生成树林。？？不是所有顶点吗？？
性质7.6 (图的生成树林的边数) 包含n个顶点、m个连通分量的无向图G的生成树林恰好n-m条边。？？归纳
遍历和生成树
从连通无向图或强连通有向图中任一顶点出发遍历，或从有根有向图的根顶点出发遍历，都可以访问到所有顶点。遍历中经过的边加上原图的所有顶点，就构成了改图的一棵生成树。
例7.10
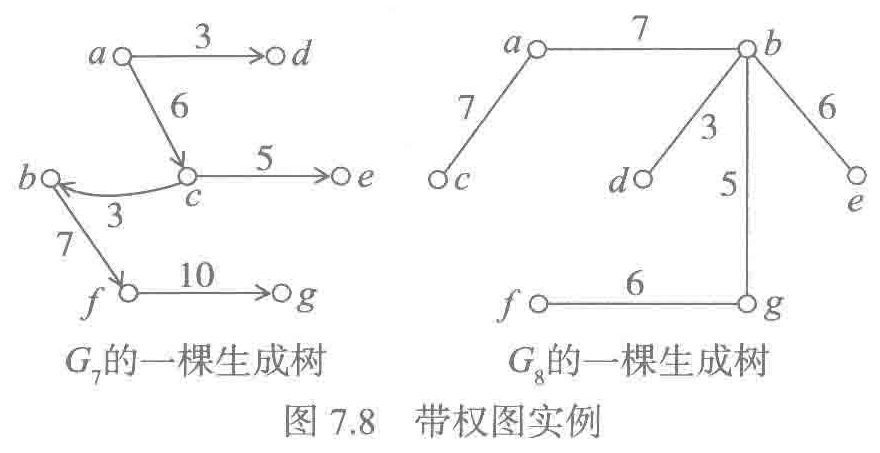是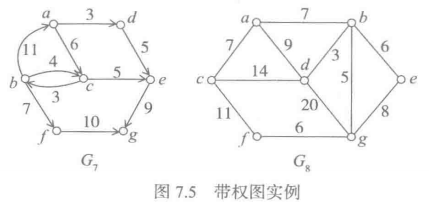
的生成树。(G7是有根有向图，G8是连通无向图)
左图是对G7从顶点a出发遍历得到的DFS生成树，右边是对G8从顶点b出发遍历得到的BFS生成树。
构造DFS生成树
需要解决两个问题：
1）如何实现DFS遍历？
2）如何构造并给出所需的DFS生成树？(生成树的顶点就是原图的顶点，关键是如何表示生成树的边)
生成树上的边形成了从初始顶点到其他顶点的一簇路径，在这簇路径里，一个顶点可能有多个“下一顶点”，但每个顶点最多有一个“前一顶点”。记录路径的一种方式是记录所有的“前一顶点”关系。有了这些信息，遍历完所有顶点之后，根据前一顶点关系就能追溯出所有的路径了。
在考虑路径上的前一顶点关系时，对应每个顶点只需记录一项信息。设图中有vnum个顶点，可以用一个包含vnum个元素的表span_forest记录得到的路径信息，令表项span_forest[vi]的形式是序对(vj, e)，其中vj是从v0到vi的路径上vi的前一顶点，e是从vj到vi的邻接边信息。
构造DFS生成树：递归算法
1 # 构造有向图G7 2 g = GraphAL() 3 for _ in range(7): 4 g.add_vertex() 5 g.add_edge(0, 2, 6) 6 g.add_edge(0, 3, 3) 7 g.add_edge(1, 0, 11) 8 g.add_edge(1, 2, 4) 9 g.add_edge(1, 5, 7) 10 g.add_edge(2, 1, 3) 11 g.add_edge(2, 4, 5) 12 g.add_edge(3, 4, 5) 13 g.add_edge(4, 6, 9) 14 g.add_edge(5, 6, 10) 15 16 # G7的生成树 17 # g.add_edge(0, 2, 6) 18 # g.add_edge(0, 3, 3) 19 # g.add_edge(1, 5, 7) 20 # g.add_edge(2, 1, 3) 21 # g.add_edge(2, 4, 5) 22 # g.add_edge(5, 6, 10) 23 print(g._mat) 24 # [ 25 # [(2, 6), (3, 3)], 26 # [(5, 7)], 27 # [(1, 3), (4, 5)], 28 # [], 29 # [], 30 # [(6, 10)], 31 # [] 32 # ] 33 34 35 def DFS_span_forest(graph): 36 vnum = graph.vertex_num() 37 span_forest = [None] * vnum # 初始值为None，表示到顶点的路径尚未找到，也表示该顶点尚未访问 38 39 def dfs(graph, v): # v为顶点序号 40 # nonlocal span_forest # 加不加这句没区别 41 for u, w in graph.out_edges(v): 42 # print('==', v, u, span_forest) # 递归和循环结合的问题要特别注意 43 if span_forest[u] is None: 44 span_forest[u] = (v, w) 45 dfs(graph, u) # 深度优先 46 47 for v in range(vnum): 48 if span_forest[v] is None: 49 span_forest[v] = (v, 0) # 先设置为顶点本身，(列表的特征决定了当下标超出合法范围时赋值会报错，但因为前面已把所有要用到的元素赋值为None，所以不会出现这个问题) 50 dfs(graph, v) 51 return span_forest 52 53 print(DFS_span_forest(g)) 54 # span_forest = [(0, 0), (2, 3), (0, 6), (0, 3), (2, 5), (1, 7), (5, 10)]
7.4 最小生成树
本节讨论的是带权连通无向图。
7.4.1 最小生成树问题
一棵生成树中各条边的权值之和称为该生成树的权。
网路G可能存在多棵权值不同的生成树，其中权值最小的生成树称为G的最小生成树。任何一个网络都有最小生成树，但其最小生成树可能不唯一。
。。。
9.1.2 排序算法
排序算法也由一些与问题相关的特有性质：
1）稳定性：如果待排序序列里任一对排序码相同的记录Ri和Rj，在排序之后的序列里Ri和Rj的前后顺序不变，就称这种排序算法是稳定的。
2）适应性：如果一个排序算法对接近有序的序列工作得更快，就称这种算法具有适应性。
内排序：待排序的数据保存在内存。外排序：待排序的数据保存在外存。归并排序算法是大多数外排序算法的基础。
排序工作要求数据集合中存在一种可用的序。如果数据本身没有自然的序，也可以构造一种序。最典型的方法是设计一种hash函数，把数据集的元素映射到某个有序集，如整数集合的子集。
9.2.1 插入排序
不断地把一个个元素插入一个序列中，最终得到排序序列。作为插入操作的起点，需要一个初始的已排序序列(无元素序列或只有一个元素的序列)。
算法的考虑和实现
由于现在考虑的是连续表排序，又希望尽可能少用辅助空间，最合适的方法是把正在构造的排序序列嵌入原来的表中。
连续表排序实例：
1 # 从小到大排序 2 def insert_sort(lst): 3 for i in range(1, len(lst)): # 初始排序序列为lst[0:1] 4 x = lst[i] 5 j = i 6 while j > 0 and lst[j-1] > x: 7 lst[j] = lst[j-1] # 如果比x大，就后移 8 j -= 1 9 lst[j] = x 10 return lst
或，
1 def insert_sort(li): 2 if len(li) < 2: 3 return li 4 i = 1 5 while i < len(li): 6 j = i-1 7 e = li[i] 8 while j >= 0 and e < li[j]: 9 li[j+1] = li[j] 10 j -= 1 11 li[j+1] = e 12 i += 1 13 return li
算法分析
空间复杂度：计算中只用了两个简单变量，用于辅助定位和完成序列元素的位置转移，因此算法的空间复杂度为O(1)，与序列大小无关。
时间复杂度：外层循环总是要执行n-1次，内层循环次数与实际比较的情况有关。最坏情况是：如果每次处理的元素比前面所有的元素都小，这个元素就会移到最前面，内层循环执行次数为j，即1+2+3+...+ (n-1)=n*(n-1)/2。最好情况是：要处理的元素总是比已排序序列的最后一个元素大，内存循环不执行，循环体只执行一次。第一种情况对应原序列逆序排列，第二张情况对应原序列已排序。基于上述分析：
1）比较次数由内层循环执行次数决定。最少为n-1次，对应上述最好情况；最多执行n(n-1)/2次，对应上述最坏情况。
2）元素移动次数包括内层循环外面的两次和循环中的若干次，最少为2*(n-1)次(x=lst[i]，lst[j]=x)，最多为2(n-1)+n*(n-1)/2次(最坏情况是比较几次，元素就移动几次)。
也就是说，最坏情况下复杂度为O(n²)，最好情况下复杂度为O(n)。算法具有适应性(越接近有序执行越快)。
算法的平均时间：显然，一个元素可能插入已排序序列的任何位置。假设插入各位置的概率相等，内存循环每次迭代的次数是j/2，求和后得到n*(n-1)/4，复杂度仍是O(n²)。
上述插入排序算法是稳定的：因为在内层循环中检索插入位置的过程中，一旦发现前面的元素与当前元素关键码相等，就不再移动元素了。这种做法保证了关键码相同的元素不会交换位置，因此算法稳定。稳定性是一个具体算法的性质，而不是排序方法的性质。
3.4.4节给出了一个单链表的插入排序算法。
插入排序是最重要的简单排序算法，原因有二：一是实现简单，二是自然的稳定性和适应性。因此经常被用于一些高级排序算法，作为其中的组成部分。例如shell排序。
9.2.2 选择排序
选择排序的基本思想：
1）维护需要考虑的所有记录中最小的i个记录的已排序序列。
2）每次从剩余未排序的记录中选取关键码最小的记录，将其放在已排序序列记录的后面，作为序列的第i+1个记录，使已排序序列增长。
3）以空序列作为排序工作的开始，做到尚未排序的序列里只剩下一个元素时，只需直接将其放在已排序的记录之后，整个排序就完成了。
除此之外，还需解决两个问题：一是如何选择元素；二是尽可能使用现有序列的存储空间。
简单选择排序
最简单的选择方法是顺序扫描序列中的元素，记住遇到的最小元素。一次扫描完毕就找到了一个最小元素，反复扫描就能完成排序工作。另一方面，选出了一个元素，原来的序列中就出现了一个空位，可以把这些空位集中起来存放排好序的序列。
1 def select_sort(lst): 2 for i in range(len(lst)): 3 k = i 4 for j in range(i+1, len(lst)): 5 if lst[j] < lst[k]: 6 k = j 7 if i != k: # 表示当前元素就是最小的，没有必要再交换。 8 lst[i], lst[k] = lst[k], lst[i] 9 return lst
或，
1 def select_sort(li): 2 k = 0 3 while k < len(li): 4 i = j = k 5 e = li[i] 6 while i < len(li): 7 if li[i] < e: 8 j = i 9 e = li[i] 10 i += 1 11 li[k], li[j] = li[j], li[k] 12 k += 1 13 return li
易见，这种直接选择排序的比较次数与被排序表的初始状态无关(有序性)，两个for循环总是按固定方式重复执行那么多次。比较的总次数为(n-1)+(n-2)+...+1=n*(n-1)/2。
记录移动的次数则依赖于具体情况。如果每次确定的k值都等于i(不经过内层for循环)，就达到了最少的移动次数0，表示序列已经是已排序序列。最坏情况是每次都交换，代码中采用了一个并行赋值(交换值的行)，可以认为移动次数为2*(n-1)。综合考虑，平均和最坏情况的时间复杂度都为O(n²)。算法没有适应性。
另一方面，算法中只用到了几个变量(i, j, k)，空间复杂度为O(1)。
算法不稳定。
试验说明，直接选择排序的实际平均排序效率都低于插入排序，因此很少被实际应用。
9.2.3 交换排序
一个序列中的记录没排好序，那么其中一定有逆序存在。如果交换所发现的逆序记录对，得到的序列将更接近排序序列；通过不断减少序列中的逆序，最终得到的就是排序序列。
起泡排序
基本操作是比较相邻记录，发现逆序对就进行交换。
图9.3展示了对一个简单序列的起泡排序过程。
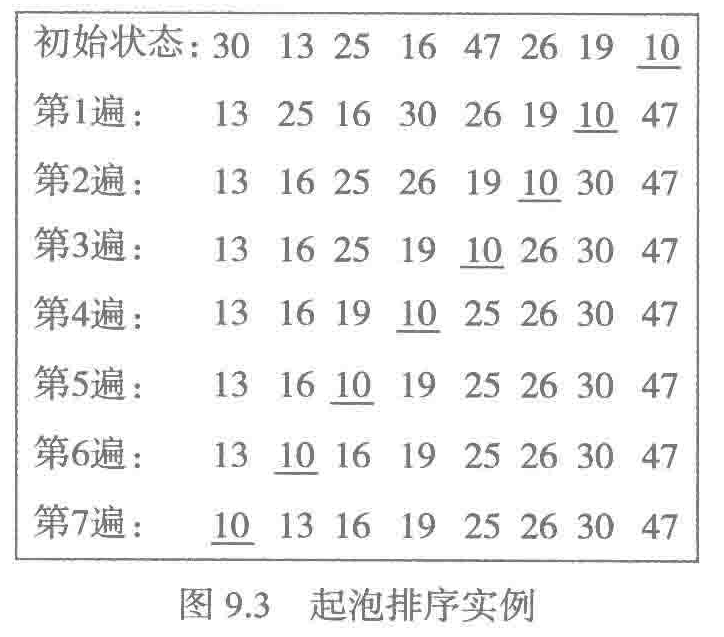
1）每一遍检查可以把一个最大元素交换到位。
2）从左到右比较，导致较小元素一次只左移一位。个别距离目标位置很远的小元素，如本例中的10，可能延误整个排序进程。
比较和交换导致较大记录右移，就像水中起泡浮起，这就是起泡排序的由来。
1 def bubble_sort(li): 2 for i in range(len(li)-1): 3 for j in range(len(li)-1-i): 4 if li[j] > li[j+1]: 5 li[j], li[j+1] = li[j+1], li[j] 6 print(li)
算法的改进
如果在一次扫描中没遇到逆序，说明排序工作已经完成，就可以提前结束了。增加一个辅助变量found。
def bubble_sort(li): for i in range(len(li)-1): found = False for j in range(len(li)-1-i): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] found = True if not found: break print(li)
这样做可以提高效率，使算法具有适应性。
最坏情况下，时间复杂度为O(n²)，平均时间复杂度也为O(n²)。改进后最好情况下时间复杂度为O(n)。起泡排序算法也是一种原位排序算法，其中使用的辅助空间为O(1)。
情况分析
试验说明，起泡排序的效率比较低，实际效果劣于复杂度相同的简单插入排序。原因有二：一是反复交换中赋值操作比较多，积累起来代价比较大。二是一些距离最终位置很远的记录可能拖累整个算法。要缓解第二个问题，应该想办法让元素大跨步地向其最终位置移动。快速排序就有这种效果。另一种简单方法是交错起泡，具体做法是一遍从左向右扫描，下一遍从右到左，交替进行。
9.3 快速排序
快速排序实现中也采用了发现逆序和交换记录位置的方法，但算法中最基本的思想是划分，即按照某种标准把记录划分为“小记录”和“大记录”，并通过递归不断划分，如此下去直到每个组中最多只有一个记录(只包含一个记录的组天然是有序的)，最终得到一个已排序的序列。
9.3.1 快排的顺序表实现
快排的思想同样可以用于链接表。
在实现排序工作时，人们希望尽可能在表的内部完成排序，尽可能少使用辅助空间。对于快排，一个重要的设计目标就是希望在原表内部实现划分。
确定划分规则：最简单的划分方式是，取序列中第一个记录为比较标准，比它小的记录移到左边，比它大的记录移到右边，划分完成后表中间将留下一个空位，这就是作为比较标准的记录的正确位置。位置一旦固定，随后的操作中不需要改变。
(一次)划分的实现
取出第一个记录记为R，为了利用这个空位，需要从表右端开始检查，把发现的第一个小记录移到左边，这一迁移操作导致表右边留下一个空位，可供存放在左边发现的一个大记录。
1 def quick_sort(li): 2 return qsort_rec(li, 0, len(li)-1) 3 4 def qsort_rec(li, l, r): # li=[10, 13, 16, 19, 25, 26, 30, 47] 5 if l >= r: # 分段无记录或只有一个记录 6 return 7 i = l 8 j = r 9 pivot = li[i] 10 while i < j: 11 while i < j and li[j] >= pivot: 12 j -= 1 13 if i < j: # 条件不能忘 14 li[i] = li[j] 15 i += 1 16 while i < j and li[i] <= pivot: 17 i += 1 18 if i < j: # 条件不能忘 19 li[j] = li[i] 20 j -= 1 21 li[i] = pivot 22 # print(li, i, j) 23 qsort_rec(li, l, i-1) # 递归处理左半区间 24 qsort_rec(li, i+1, r) # 递归处理右半区间 25 return li 26 27 li = [30, 13, 25, 16, 47, 26, 19, 10] 28 print(quick_sort(li))
9.3.3 复杂度
设定被排序序列中的记录个数为n。很容易确认，在整个快排算法的工作过程中，记录移动次数不大于比较次数，因此只需考虑比较次数。而比较次数与划分的情况有关：
1）如果每次划分都把所处理区域划分为长度基本相等的两端，只需大约logn层划分就能使最下层的每个分段长度不超过1。而在划分一层记录的过程中，关键码比较次数不超过序列长度n(每层都有些枢轴元素不需要比较，而且越往下枢轴元素越多)，综合起来可知，排序中关键码的比较次数不超过O(n*logn)。
2）如果每层划分得到的两段中总有一段为空，另一段记录个数只比本层划分之前少一个(枢轴元素)，这种情况下，要使所有分段的长度不大于1，就要做n-1层划分。完成各层划分的比较次数从n-1逐层减少到1。(n-1)+(n-2)+...+2+1=(n-1)*n/2次。
由上述分析可知，快排的最好情况不超过(n*logn)，最坏情况为O(n²)。
快排产生的划分结构，可以看作以枢轴元素为根，以两个划分分段进一步划分的结果作为左右子树的二叉树。根据二叉树理论，所有n个结点的二叉树的平均高度为(logn)。因此，快排的平均时间复杂度为O(n*logn)。
排序低效的原因是分段不均衡，根源是划分标准没有选好。为此，可以考虑修改划分依据。三者取中规则：每趟划分前比较分段中第一个、最后一个和位置居中三个记录的关键码，取其中值居中的记录与首元素交换位置，而后基于这个记录的关键码做划分。这种做法可以减少最坏情况出现的概率，但无法消除最坏情况。
不具有稳定性。不会因为原序列接近有序而更高效，因此不具有适应性。
9.4 归并排序
把两个或多个有序序列合并为一个有序序列。
基本方法：
1）初始时，把待排序序列中的n个记录看成n个有序子序列，每个子序列的长度为1。
2）把当前序列组里的有序子序列两两归并，完成一遍归并后组里的序列个数减半，每个子序列的长度加倍。
3）对加长的有序子序列重复第二步操作，最终得到一个长度为n的有序序列。
这种归并方法称为简单的二路归并排序(把两个序列归并为一个)。也可以考虑三路归并或更多路归并。
归并操作是一种顺序性操作，其中按自然存在的顺序使用被排序序列，也按顺序产生归并后的结果序列。外存数据比较适合顺序处理，但不适合随机访问。所以归并操作适合处理外存数据。很多外存数据排序算法都是基于归并操作实现的。
9.4.1 顺序表的归并排序
9.4.2 归并算法的设计问题
第一个问题，在一遍遍的归并过程中，作为归并结果的序列放在哪里。原地归并比较复杂，更简单的方式是另外开辟一片同样大小的存储区，把一遍归并的结果放在那里。在完成一遍归并后，在保存归并结果的新表里存储着长度加倍的有序序列，而原来的表闲置了。这样来回做几遍就能完成整个排序工作了。
归并操作至少需要O(n)的辅助空间，这是付出空间代价，获得算法实现的简便性，在实际中经常这样做。
9.4.3 归并排序函数定义
参考图9.7，可以看到归并排序的工作分为几个层次：最上层控制一遍遍归并，完成整个表的排序工作；在一遍遍处理中需要分别完成一对对递增序列的归并；在归并每一对序列中又需要一个个地处理序列元素。分三层实现：
1）最下层：实现表中相邻的一对有序序列的归并工作，将归并的结果存入另一个顺序表里的相同位置。
2）中间层：基于操作1，实现对整个表里顺序各对有序序列的归并，完成一遍归并，各对序列的归并结果存入另一个顺序表里的同位置分段。
3）最高层：在两个顺序表之间往复执行操作2，完成一遍归并后交换两个表的地位，然后再重复操作2的工作，直至整个表里只有一个有序序列时排序完成。
1 # 实现最下层，把两个有序序列归并为一个有序序列 2 def merge(lfrom, lto, low, mid, high): 3 ''' 4 :param lfrom: 5 :param lto: 6 :param low: 第一分段开头的索引 7 :param mid: 第二分段开头的索引 8 :param high: 第二分段结尾的索引 9 :return: 10 ''' 11 i, j, k = low, mid, low 12 while i < mid and j < high: # 反复复制两分段首中较小的记录 13 if lfrom[i] <= lfrom[j]: 14 lto[k] = lfrom[i] 15 i += 1 16 else: 17 lto[k] = lfrom[j] 18 j += 1 19 k += 1 20 while i < mid: # 可能第二段中已经复制完，但第一段中仍有记录，剩下的都是较大的，直接复制到lto 21 # 因为是直接复制过来的，所以剩余部分未必是有序的 22 lto[k] = lfrom[i] 23 i += 1 24 k += 1 25 while j < high: # 同上 26 lto[k] = lfrom[j] 27 j += 1 28 k += 1 29 30 31 # 中间层，完成一遍归并 32 def merge_pass(lfrom, lto, llen, slen): 33 ''' 34 :param lfrom: 35 :param lto: 36 :param llen: 表长度 37 :param slen: 分段长度 38 :return: 39 ''' 40 i = 0 41 while i + 2 * slen < llen: # 归并长为slen的两分段，不足长的分段不归并 42 merge(lfrom, lto, i, i+slen, i+2*slen) 43 i += 2 * slen 44 # print(lfrom, lto) 45 if i + slen < llen: # 剩下两段，第二段长度小于slen 46 merge(lfrom, lto, i, i+slen, llen) 47 else: # 剩下一段，直接复制到lto 48 for j in range(i, llen): 49 lto[j] = lfrom[j] 50 51 52 def merge_sort(lst): 53 slen, llen = 1, len(lst) 54 templst = [None]*llen 55 while slen < llen: 56 merge_pass(lst, templst, llen, slen) 57 slen *= 2 58 merge_pass(templst, lst, llen, slen) # 结果存回原位 59 slen *= 2 60 61 lfrom = [25, 67, 54, 33, 20, 78, 65, 49, 17, 56, 44] 62 lto = [None] * len(lfrom) 63 merge_sort(lfrom)
整个序列的实际排序完成时，得到的结果有可能正好放在templst里，这时再执行一次merge_pass就能把结果复制回原来的lst。
9.4.4 算法分析
时间复杂度：易见，做完第k遍归并后，有序子序列的长度为2k。因此完成整个排序需要做的归并遍数不会多于logn+1。进而，在每遍归中做的比较次数为O(n)，(比较次数单指元素之间的比较，条件判断中的比较没有计入)，所以总的比较次数和移动次数都为O(n*logn)，(比较一次移动一次)。
空间复杂度：算法里使用了一个与原表长度相同的辅助表，因此空间复杂度为O(n)。
上述给出的算法在关键码相同时采用左序列元素先行的原则，保证了稳定性。
对任何序列都要做logn遍归并，没有适应性。
9.5 其他排序方法
9.5.1 分配排序和基数排序
之前介绍的算法都是基于(关键码)比较的思想，现在介绍基于一种固定位置的分配和收集。
分配与排序
适用条件：关键码只有很少几个不同的值。
思路：
1）为每个关键码值设定一个桶(即能容纳任意多个记录的容器，例如用一个连续表或链接表)。
2）根据关键码把记录放入相应桶中。
3）存入所有记录后，顺序收集各个桶里的记录，就得到了排序的序列。
实例：按成绩绩点对全校学生的学习记录排序。由于绩点只有2位数字，只需几十个可能值，每个绩点设置一个桶，通过一遍记录分配和一遍收集，就能得到稳定排序的结果。算法设计合理的话，可以在O(n)时间内完成，复杂度低于采用关键码比较排序的最优算法。
多轮分配和排序
如果只允许为数不多的一小批桶，分配排序方法的应用范围就太窄了。多轮分配方法是对分配排序方法的扩充。其中采用元组(其元素适合分配排序)作为关键码，通过多轮分配和收集，完成以这种元组为关键码的记录的排序工作。
实例：假定以(a, a, a)形式的三元组作为关键码，其中a为数字，取值来自集合{0, 1, 2, 3}，待排序关键码序列如下：
多轮分配可以从最高位或最低位开始。采用高位优先方法需要考虑越来越多的子序列，实现比较麻烦。低位优先方法的思路：
1）首先按第3位元素进行分配，如图9.9
然后将记录顺序收集，各关键码最后一位分段递增。
2）再按关键码的中间元素分配和收集，只要注意维持稳定性，在得到的每个分段中仍然可以保证最后一位递增。如果9.10
然后再将记录顺序收集，得到的序列是按后两位递增排序的。
3）再针对最高位做一遍分配和收集，就能得到按整个三位排序的关键码序列。
如果每位关键码都是数字，关键码元组就像是某种进制表示的一个整数，排序过程中就是从低到高逐位分配和收集，这样的处理过程就像是按基数逐位处理，因此这种多轮分配排序也称为基数排序。
9.5.3 python系统的list排序
python内置方法sort，list的sort方法，共享Timsort。
蒂姆排序是一种基于归并技术的稳定排序算法，其中结合使用了归并排序和插入排序技术，最坏时间复杂度为O(n*logn)。
