简单易学的机器学习算法——协同过滤推荐算法(1)
一、推荐系统的概念
推荐系统(Recommendation System, RS),简单来说就是根据用户的日常行为,自动预测用户的喜好,为用户提供更多完善的服务。举个简单的例子,在京东商城,我们浏览一本书之后,系统会为我们推荐购买了这本书的其他用户购买的其他的书:
推荐系统在很多方面都有很好的应用,尤其在现在的个性化方面发挥着重要的作用。
二、推荐系统的分类
推荐系统使用了一系列不同的技术,主要可以分为以下两类:
- 基于内容(content-based)的推荐。主要依据的是推荐项的性质。
- 基于协同过滤(collaborative filtering)的推荐。主要依据的是用户或者项之间的相似性。
- 基于项(item-based)的推荐系统。主要依据的是项与项之间的相似性。
- 基于用户(user-based)的推荐系统。主要依据的是用户与用户之间的相似性。
三、相似度的度量方法
相似性的度量的方法有很多种,不同的度量方法的应用范围也不一样。相似性度量方法的设计也是机器学习算法设计中很重要的一部分,尤其是对于聚类算法,推荐系统这类算法。
相似性的度量方法必须满足拓扑学中的度量空间的基本条件:
假设 是度量空间
是度量空间 上的度量:
上的度量: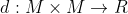 ,其中度量
,其中度量 满足:
满足:
- 非负性:
,当且仅当
时取等号;
- 对称性:
;
- 三角不等性:
。
1、欧式距离
欧式距离是使用较多的相似性的度量方法,在kMeans中就使用到欧式距离作为相似项的发现。
2、皮尔逊相关系数(Pearson Correlation)
在欧氏距离的计算中,不同特征之间的量级对欧氏距离的影响比较大,例如) ,
,) 和
和) ,我们就不能很好的利用欧式距离判断
,我们就不能很好的利用欧式距离判断 和
和 ,
, 和
和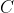 之间的相似性的大小。而皮尔逊相似性的度量对量级不敏感:
之间的相似性的大小。而皮尔逊相似性的度量对量级不敏感:
其中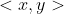 表示向量
表示向量 和向量
和向量 内积,
内积,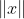 表示向量
表示向量 的二范数。
的二范数。
3、余弦相似度(Cosine Similarity)
余弦相似度有着与皮尔逊相似度同样的性质,对量级不敏感,是计算两个向量的夹角。在吴军老师的《数学之美》上,在计算文本相似性的过程中,大量使用了余弦相似性的度量方法。
四、基于相似度的推荐系统
协同过滤是通过将用户和其他用户的数据进行对比来实现推荐的。我们通过一个评分系统对基于协同过滤的推荐系统作阐述。
(不同用户对不同商品的评分)
如图,横轴为每个用户对不同商品的评分,评分的范围为1~5,0表示该用户未对该商品评分。我们以用户Tracy为例,Tracy未对日式炸鸡排和寿司饭评分,我们利用协同过滤推荐系统预测Tracy对该两个商品评分,并依据分数的高低向Tracy推荐商品。
1、计算相似度
在本例中,我们是依据物品的相似度,即计算日式炸鸡排与鳗鱼饭、烤牛肉和手撕猪肉的相似度实现对日式炸鸡排的评分,用同样的方法对寿司饭评分。
2、排序
排序的目的是实现在日式炸鸡排与寿司饭这两个商品中推荐给用户Tracy。
3、实验结果
(相似度的计算——基于余弦相似度)
(推荐结果)
从推荐结果,我们发现寿司饭的评分更高,首推寿司饭,日式炸鸡排排在寿司饭后面。
4、MATLAB代码
主程序
- %% 主函数
- % 导入数据
- data = [4,4,0,2,2;4,0,0,3,3;4,0,0,1,1;1,1,1,2,0;2,2,2,0,0;1,1,1,0,0;5,5,5,0,0];
- % reccomendation
- [sortScore, sortIndex] = recommend(data, 3, 'cosSim');
- len = size(sortScore);
- finalRec = [sortIndex, sortScore];
- disp(finalRec);
计算相似度的函数
- function [ score ] = evaluate( data, user, simMeas, item )
- [m,n] = size(data);
- simTotal = 0;
- ratSimTotal = 0;
- % 寻找用户都评价的商品
- % data(user, item)为未评价的商品
- for j = 1:n
- userRating = data(user, j);%此用户评价的商品
- ratedItem = zeros(m,1);
- numOfNon = 0;%统计已评价商品的数目
- if userRating == 0%只是找到已评分的商品
- continue;
- end
- for i = 1:m
- if data(i,item) ~= 0 && data(i,j) ~= 0
- ratedItem(i,1) = 1;
- numOfNon = numOfNon + 1;
- end
- end
- % 判断有没有都评分的项
- if numOfNon == 0
- similarity = 0;
- else
- % 构造向量,便于计算相似性
- vectorA = zeros(1,numOfNon);
- vectorB = zeros(1,numOfNon);
- r = 0;
- for i = 1:m
- if ratedItem(i,1) == 1
- r = r+1;
- vectorA(1,r) = data(i, j);
- vectorB(1,r) = data(i, item);
- end
- end
- switch simMeas
- case {'cosSim'}
- similarity = cosSim(vectorA,vectorB);
- case {'ecludSim'}
- similarity = ecludSim(vectorA,vectorB);
- case {'pearsSim'}
- similarity = pearsSim(vectorA,vectorB);
- end
- end
- disp(['the ', num2str(item), ' and ', num2str(j), ' similarity is ', num2str(similarity)]);
- simTotal = simTotal + similarity;
- ratSimTotal = ratSimTotal + similarity * userRating;
- end
- if simTotal == 0
- score = 0;
- else
- score = ratSimTotal./simTotal;
- end
- end
推荐函数
- function [ sortScore, sortIndex ] = recommend( data, user, simMeas )
- % 获取data的大小
- [m, n] = size(data);%m为用户,n为商品
- if user > m
- disp('The user is not in the dataBase');
- end
- % 寻找用户user未评分的商品
- unratedItem = zeros(1,n);
- numOfUnrated = 0;
- for j = 1:n
- if data(user, j) == 0
- unratedItem(1,j) = 1;%0表示已经评分,1表示未评分
- numOfUnrated = numOfUnrated + 1;
- end
- end
- if numOfUnrated == 0
- disp('the user has rated all items');
- end
- % 对未评分项打分,已达到推荐的作用
- itemScore = zeros(numOfUnrated,2);
- r = 0;
- for j = 1:n
- if unratedItem(1,j) == 1%找到未评分项
- r = r + 1;
- score = evaluate(data, user, simMeas, j);
- itemScore(r,1) = j;
- itemScore(r,2) = score;
- end
- end
- %排序,按照分数的高低进行推荐
- [sortScore, sortIndex_1] = sort(itemScore(:,2),'descend');
- [numOfIndex,x] = size(sortIndex_1(:,1));
- sortIndex = zeros(numOfIndex,1);
- for m = 1:numOfIndex
- sortIndex(m,:) = itemScore(sortIndex_1(m,:),1);
- end
- end
相似度的函数:
- 欧式距离函数
- function [ ecludSimilarity ] = ecludSim( vectorA, vectorB )
- ecludSimilarity = 1./(1 + norm(vectorA - vectorB));
- end
- 皮尔逊相关系数函数
- function [ pearsSimilarity ] = pearsSim( vectorA, vectorB )
- pearsSimilarityMatrix = 0.5 + 0.5 * corrcoef(vectorA, vectorB);
- pearsSimilarity = pearsSimilarityMatrix(1,2);
- end
- 余弦相似度函数
- function [ cosSimilarity ] = cosSim( vectorA, vectorB )
- %注意vectorA和vectorB都是行向量
- num = vectorA * vectorB';
- denom = norm(vectorA) * norm(vectorB);
- cosSimilarity = 0.5 + 0.5 * (num./denom);
- end




