从模型坐标到屏幕坐标

在 3D 引擎中，场景通常被描述为三维空间中的模型或对象，每个模型对象由许多三维顶点组成。最终，这些模型对象将在平面屏幕上呈现和显示。

渲染场景始终相对于摄像机，因此，还必须相对于摄像机的视图定义场景的顶点。了解一下这个转换过程是相当有必要的。

一般从模型坐标到我们可看到在屏幕中的坐标要经过4步变化。

• 模型坐标 -> 世界坐标
• 世界坐标-> 相机坐标
• 相机坐标 -> NDC
• NDC > 屏幕坐标

NDC是Normalized Device Coordinates 的缩写，所谓Normalized Device就是指xyz三个轴向都是-1到1的空间

在 Webgl绘制图形时，顶点着色器将处理每个顶点，期望在剪辑空间中定义顶点的位置。模型视图投影是一系列常见的矩阵转换，可应用于模型空间中定义的顶点，将其转换为剪辑空间，然后可以对其进行栅格化。

定义矩阵

P1 = 模型中的点 point matrix

{
 -5.00
  5.00
  5.00
  1.00
}

M = 模型世界坐标 world matrix

{
  1.00 0.00 0.00 0.00
  0.00 1.00 0.00 5.00
  0.00 0.00 0.00 1.00
  0.00 0.00 0.00 1.00
}

世界向偏移5个单位，使结果看起来有意义。一般世界坐标是0,0,0。

V = 相机 camera matrix invert

{
  0.96 -0.00  0.28  0.00
  0.17  0.80 -0.57 -4.01
 -0.22  0.60  0.77 -45.71
  0.00  0.00  0.00  1.00
}

P = 投影坐标 camera projection matrix

{
  1.50  0.00  0.28  0.00
  0.00  2.75  0.00  0.00 
  0.00  0.00 -1.20 -22.00
  0.00  0.00 -1.00  0.00
}

W = 视口坐标 camera projection matrix

{
701.50      0.00    0.00  701.50
  0.00   -384.00    0.00  384.00 
  0.00      0.00    0.00    0.00
  0.00      0.00    0.00    1.00
}

在上述矩阵准备好后，后续可进行计算。

转换

第一步 模型坐标 -> 世界坐标

计算出P1在模型世界位置MP1

MP1 = M * P1

第二步 世界坐标-> 相机坐标

计算出P1在相机中的位置VMP1

VMP1 = V*MP1

第三步 相机投影坐标-> NDC

1. 计算出P1在相机中的位置PVMP1
2. 将4Dvector转为3Dvector，获得 NDC

PVMP1= P*VMP1 
NDC = PVMP1 / PVMP1.W // -0.15 0.02 0.57 1.00

第四步 NDC > 屏幕坐标

通过上述四步获取最终视口中的坐标599px,393px。

示例

通过代码角度更容易理解上述过程

/*
    立方体:
  - 大小 10x10x10
  - 世界坐标 (0, 5, 0) 

  桔色小球的坐标，在立方体的左上角，(-5, 5, 5)
*/

// cube.position.y = 5
// cube.add(sphere)
// sphere.position.set(-5, 5, 5)

const point = sphere.position.clone(); // (-5, 5, 5) 
console.log("point=", point);

//
// A: Model -> World
//

const M = cube.matrixWorld;
console.log("Model (World) Matrix", M);
point.applyMatrix4(M);
console.log("world-space point=", point);

//
// B: World -> Camera (aka View)
//

const V = camera.matrixWorldInverse;
console.log("View Matrix", V);
point.applyMatrix4(V);
console.log("view-space point=", point);

//
// C: Camera -> NDC
//

const P = camera.projectionMatrix;
console.log("Projection Matrix", P);
point.applyMatrix4(P);
console.log("clip coordinates", point);

//
// D: NDC -> Screen
//

const W = new THREE.Matrix4();
const { x: WW, y: WH } = renderer.getSize(new THREE.Vector2());
W.set(
  WW / 2, 0, 0, WW / 2,
  0, -WH / 2, 0, WH / 2,
  0, 0, 0.5, 0.5,
  0, 0, 0, 1
);
console.log("Window Matrix", W);
point.applyMatrix4(W);
console.log("window coordinates", point);

用一张图更容易看懂这个过程:

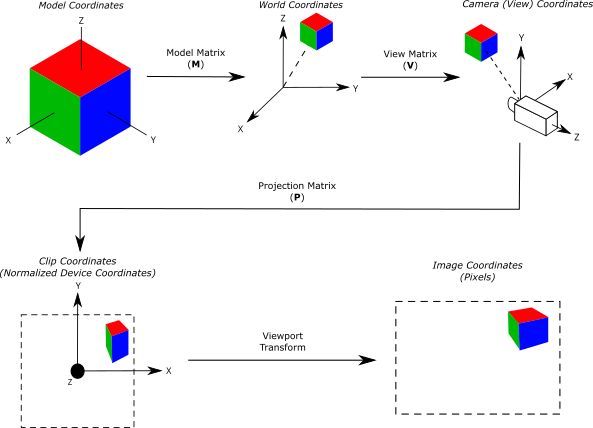
相关的文章

https://webgl2fundamentals.org/webgl/lessons/zh_cn/webgl-matrix-naming.html
https://jsantell.com/model-view-projection/