实现二叉树非递归前序、中序和后序遍历

引言

本文只讲述二叉树的三种非递归遍历，递归遍历太简单就不说了。题目分别是leetcode的94、144和145，读者阅读完后可自行去解答。使用的语言是java，其他语言读者自行操作。

正文

以下图为例讲解三种非递归遍历

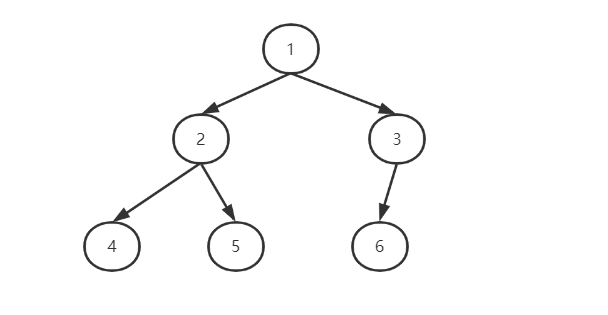
树节点的定义

public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {}
        TreeNode(int val) { this.val = val; }
        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

前序遍历

实现非递归操作，栈是不可缺少的数据结构。前序遍历是中左右，所以每次先将节点入栈，然后将右孩子入栈，再将左孩子入栈。因为栈是先进后出，这样就可以实现中左右。详细代码如下

public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        stack.add(root);
        while (!stack.isEmpty()){
            TreeNode tn = stack.pop();
            if (tn != null){
                // 中左右：先放右孩子，再放左孩子
                res.add(tn.val);
                stack.add(tn.right);
                stack.add(tn.left);
            }
        }
        return res;
    }

后序遍历

后序遍历是左右中，前序遍历中左右。根据上述前序遍历的代码我们知道如果将

stack.add(tn.right);
stack.add(tn.left);

替换成

stack.add(tn.left);
stack.add(tn.right);

此时，打印树的遍历顺序为中右左。而后序遍历是左右中，所以我们最后可以通过反转函数将res数组反转就变成了后序遍历的结果。详细代码如下

public List<Integer> postorderTraversal_01(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        stack.add(root);
        while (!stack.isEmpty()){
            TreeNode tn = stack.pop();
            if (tn != null){
                // 左右中：先放左孩子，再放有右孩子 变成中右左，然后反转变成左右中
                res.add(tn.val);
                stack.add(tn.left);
                stack.add(tn.right);
            }
        }
        // 反转
        Collections.reverse(res);
        return res;
    }

但这种方法效率不高，在leetcode评分不高，接下来换另一种方法。

使用curr作为当前树节点，pre作为上一次访问的节点（初始化为空）。curr一直遍历到最左端，当为空时弹出栈顶元素，并令curr等于栈顶元素，查看curr右孩子是否为空或者是否==pre,如果不空并且不是上次一访问的元素，则说明curr有右孩子，则需要将curr重新放进去，并令curr=curr.right，此时重新循环再遍历右子树。

但如果curr的右孩子为空或者curr的右孩子是上一次访问过的节点这两种情况其中的一种。先说curr右孩子为空，例如上图的节点3，此时左节点访问完，不存在右节点，那么按照后序遍历顺序就需要访问根节点了，于是弹出栈顶元素,并修改curr和pre的值。

如果curr的右孩子不空，但是是上一次访问过的节点。这里提出一个疑问，为什么要设置pre这一节点。用上图来说，假设当我们弹出栈顶元素2时，发现他有右孩子，此时我们将curr值设置为栈顶元素右孩子5。但是当我们遍历完5后，又需要弹出栈顶元素，此时栈顶元素依旧是2，而我们又会判断2节点右孩子是否为空，不为空则继续刚刚操作。但是刚刚操作我们已经执行了，这就陷入了死循环。所以我们需要一个pre来防止我们陷入死循环。详细代码如下

public List<Integer> postorderTraversal_02(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        TreeNode pre = null;  // 上一次访问过的节点,避免死循环
        while (curr != null || !stack.isEmpty()){
            // 遍历到最左下端
            while (curr != null){
                stack.push(curr);
                curr = curr.left;
            }
            // 弹出栈顶元素
            curr = stack.pop();
            if (curr.right == null || curr.right == pre){
                res.add(curr.val);
                pre = curr;
                curr = null;
            }else {
                // 再将栈顶元素放进去，因为他还有右子树
                stack.push(curr);
                curr = curr.right;
            }
        }
        return res;
    }

中序遍历

中序遍历跟后序遍历就相对于简单了，按照中序遍历顺序，先是左子树、节点，然后右子树。详细代码如下。

// 非递归中序遍历
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (curr != null || !stack.empty()){
            // 左不空入栈
            while (curr != null){
                stack.push(curr);
                curr = curr.left;
            }
            // 左空出栈顶元素
            curr = stack.pop();
            res.add(curr.val);
            curr = curr.right;
            }
        return res;
    }