机器学习入门--------线性回归的损失和优化

引言

假如现存在一个房屋价格和一些数据的关系，真实关系是：真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

那么现在呢，我们随意指定一个关系（猜测）随机指定关系：预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率

这样会发现真实结果与我们预测的结果存在一定的误差，如下图

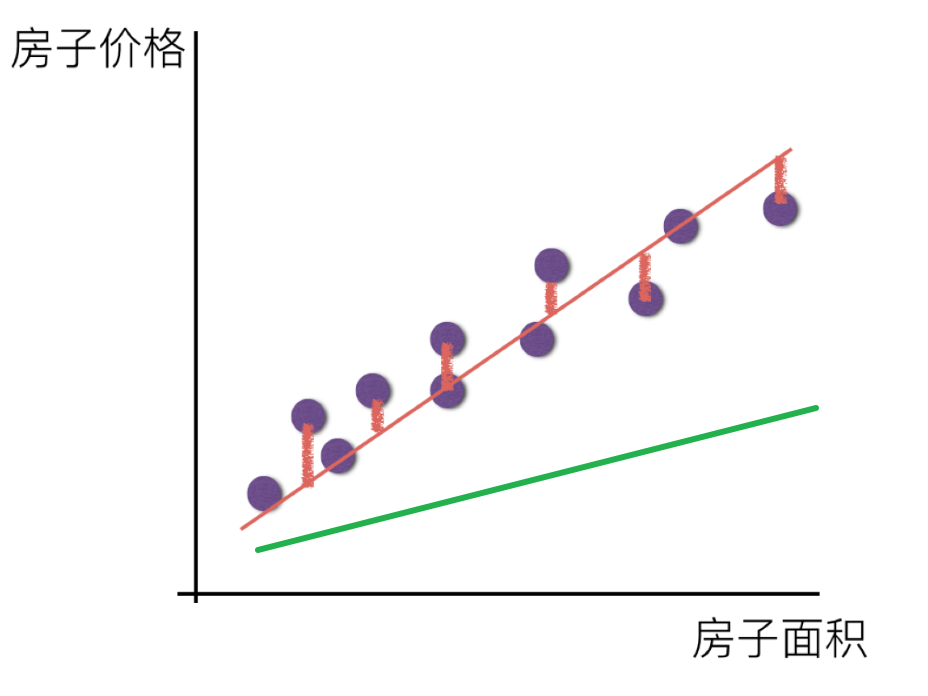
那么存在误差就需要将误差衡量出来，并尽可能减小这个误差，就有了损失函数

正文

损失函数

定义:

• yi为第i个训练样本的真实值
• h(xi)为第i个训练样本特征值组合预测函数
• 又称最小二乘法
  

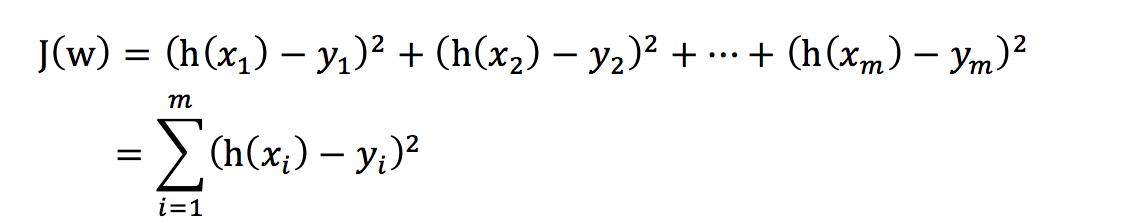
优化方法:

• 正规方程
• 梯度下降法

正规方程

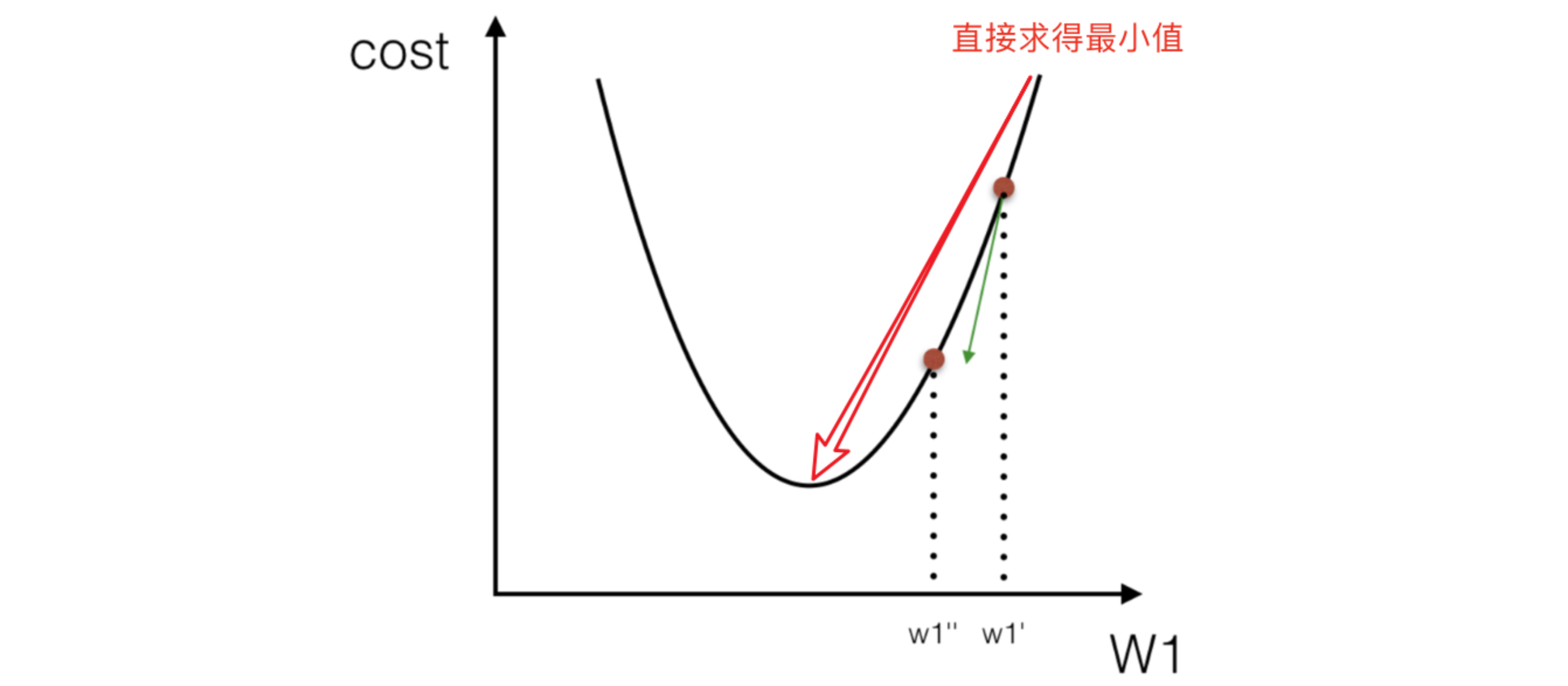
定义:X为特征值矩阵，y为目标值矩阵,xT为x的转置矩阵。

优点:直接求到最好的结果

缺点:当特征过多过复杂时，求解速度太慢并且得不到结果,时间复杂度高

代码api:

• sklearn.linear_model.LinearRegression(fit_intercept=True)
  • 通过正规方程优化
  • 参数
    • fit_intercept：是否计算偏置(y=ax+b 此时b就是偏置)
  • 属性
    • LinearRegression.coef_：回归系数(y=ax+b 此时a就是回归系数)
    • LinearRegression.intercept_：偏置

梯度下降

定义:梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要从山上下来(i.e. 找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，（同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走）。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

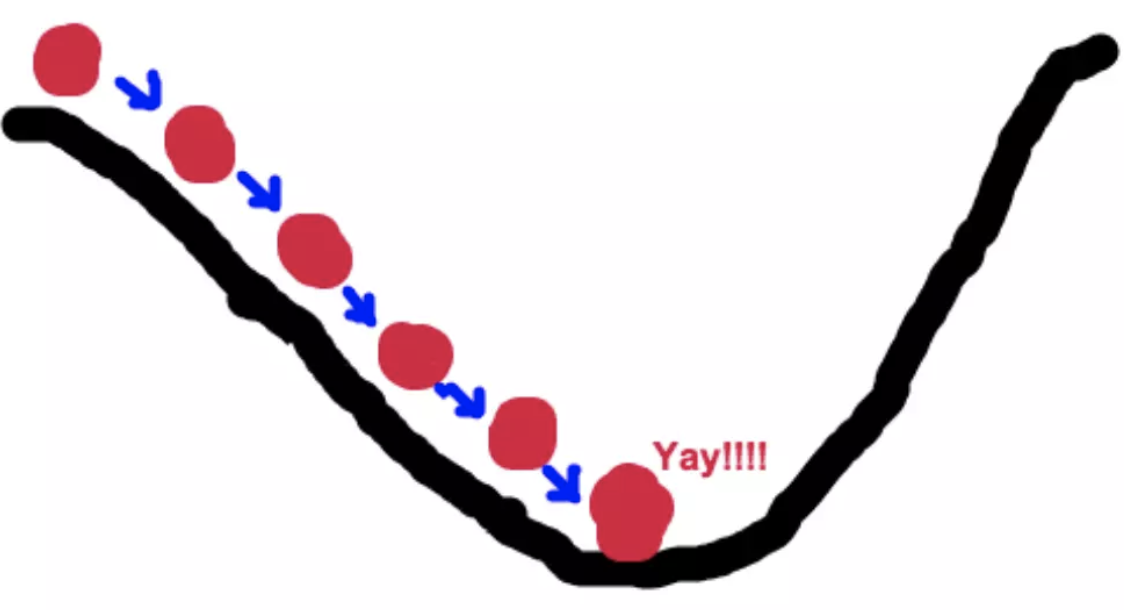
梯度下降的基本过程就和下山的场景很类似。首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数值变化最快的方向。 所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。

梯度下降公式:

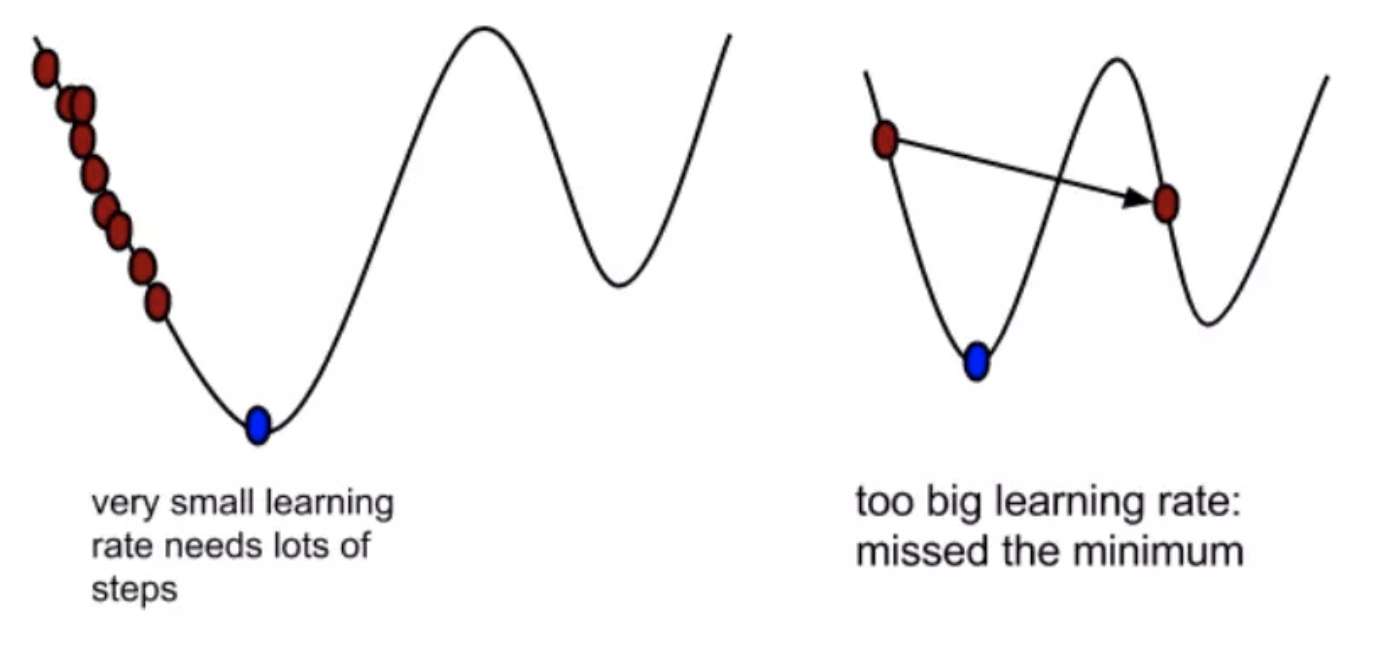
• 1）α是什么含义？

α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大扯着蛋，哈哈，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

• 2）为什么梯度要乘以一个负号？

梯度前加一个负号，就意味着朝着梯度相反的方向前进！我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号

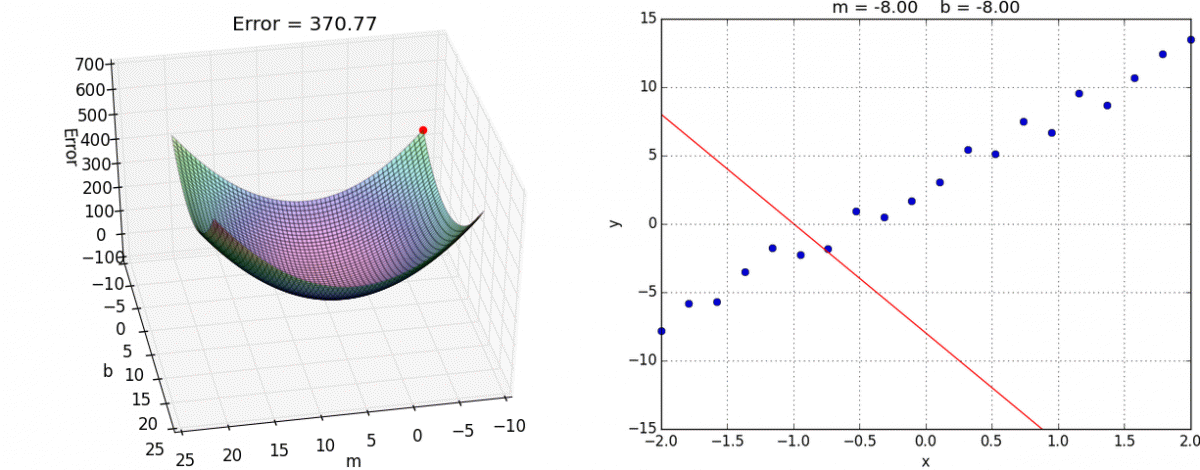
所以有了梯度下降这样一个优化算法，回归就有了"自动学习"的能力。优化动态图演示

代码api:

• sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)
  • SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
  • 参数：
    • loss:损失类型
      • loss=”squared_loss”: 普通最小二乘法
    • fit_intercept：是否计算偏置
    • learning_rate : string, optional
      • 学习率填充
      • 'constant': eta = eta0
      • 'optimal': eta = 1.0 / (alpha * (t + t0)) [default]
      • 'invscaling': eta = eta0 / pow(t, power_t) power_t=0.25:存在父类当中
      • 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
  • 属性：
    • SGDRegressor.coef_：回归系数
    • SGDRegressor.intercept_：偏置

梯度下降和正规方程的对比

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

算法选择依据：

• 小规模数据：
  • 正规方程：LinearRegression(不能解决拟合问题)
  • 岭回归
• 大规模数据：
  • 梯度下降法：SGDRegressor

案例：波士顿房价预测

通过正规方程和梯度下降分别实现房价的预测

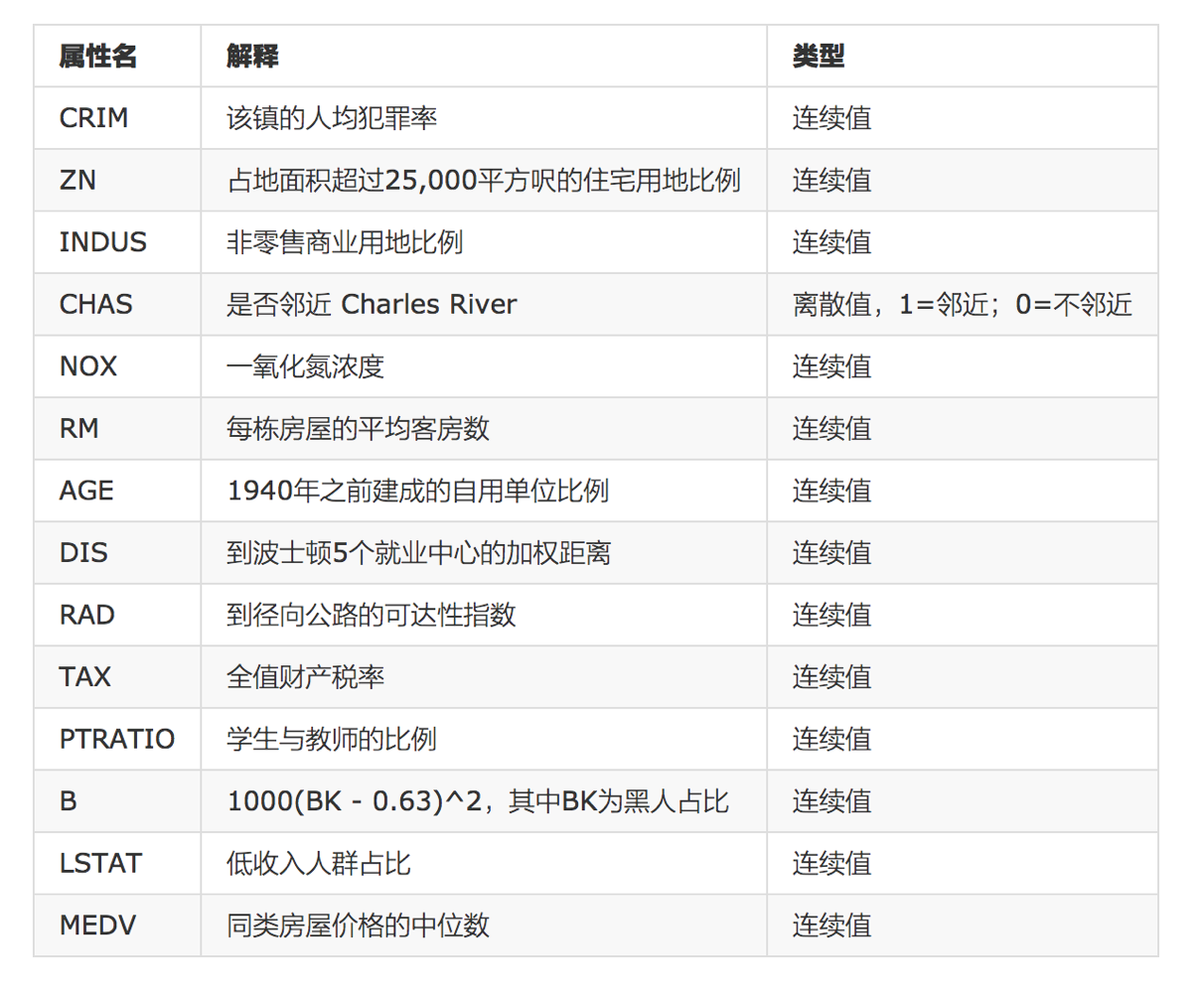
数据介绍

代码

#-*- codeing = utf-8 -*-
#@Time : 2021/1/16 19:41
#@Author : 杨晓
#@File : price_predict.py
#@Software: PyCharm
'''
# 1、获取数据
# 2、数据处理
# 2.1、数据分割
# 3、特征工程:标准化
# 4、机器学习:正规方程
# 5、模型评估
'''
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error

## 正规方程
def linear_model1():
    # 1、获取数据
    boston = load_boston()
    # 2、数据处理
    # 2.1、数据分割
    x_train,x_test,y_train,y_test = train_test_split(boston.data,boston.target,test_size=0.2)
    # 3、特征工程:标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)
    # 4、机器学习:正规方程
    estimator = LinearRegression()
    estimator.fit(x_train,y_train)
    # 5、模型评估
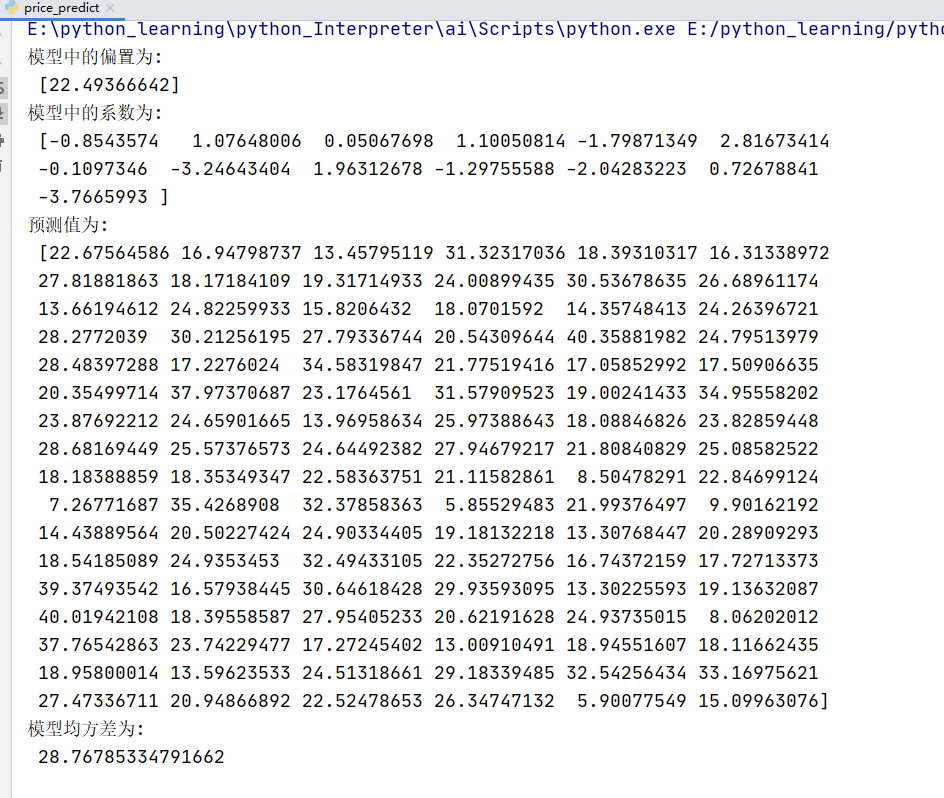
    print("模型中的偏置为:\n",estimator.intercept_)
    print("模型中的系数为:\n",estimator.coef_)
    y_pre = estimator.predict(x_test)
    print("预测值为:\n",y_pre)
    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test,y_pre)
    print("模型均方差为:\n",error)

## 梯度下降
def linear_model2():
    # 1、获取数据
    boston = load_boston()
    # 2、数据处理
    # 2.1、数据分割
    x_train,x_test,y_train,y_test = train_test_split(boston.data,boston.target,test_size=0.2)
    # 3、特征工程:标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)
    # 4、机器学习:正规方程
    estimator = SGDRegressor(max_iter=100)
    estimator.fit(x_train,y_train)
    # 5、模型评估
    print("模型中的偏置为:\n",estimator.intercept_)
    print("模型中的系数为:\n",estimator.coef_)
    y_pre = estimator.predict(x_test)
    print("预测值为:\n",y_pre)
    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test,y_pre)
    print("模型均方差为:\n",error)
#linear_model1()
linear_model2()

运行结果:

正规方程

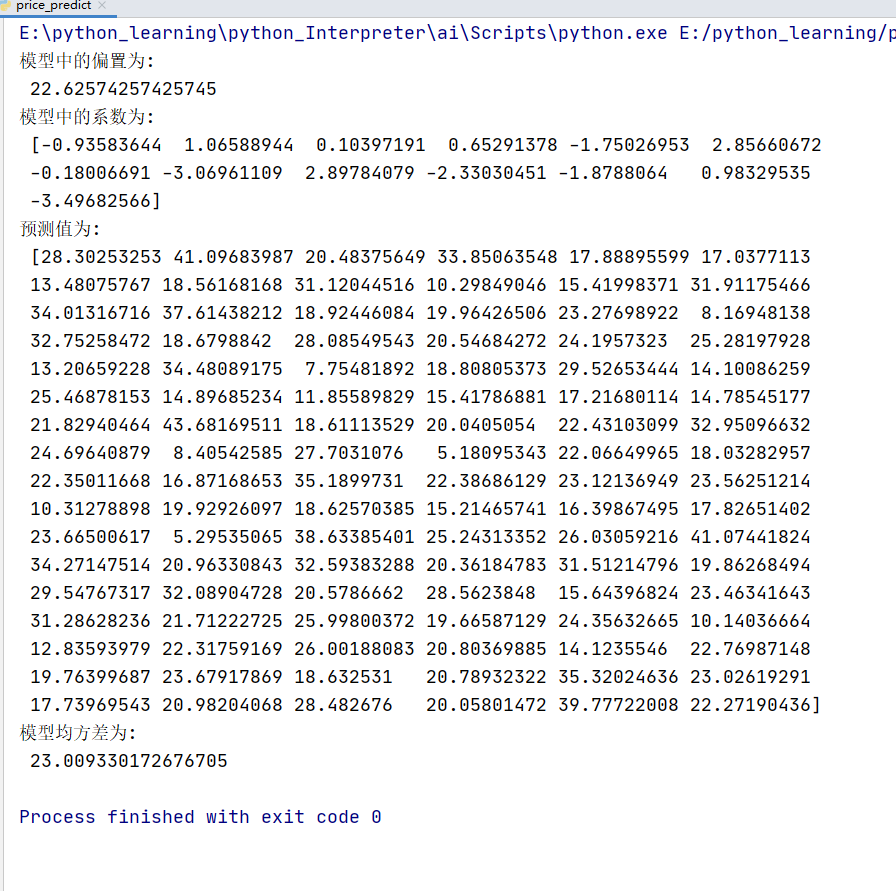
梯度下降