2-1. 矩阵论（笔记）

Course：矩阵理论
Textbook：《矩阵理论》- 黄廷柱，《矩阵论》- 方保镕
ISBN：9787040119428, 9787302092087
Link：工程应用数学基础 - 国防科技大学

一、线代基础

1.1. 线性空间

1.1.1. 线性空间

数环
数环是一种特殊的数集，字面意思由数组成的环，是环的最基本的例子和模型。设 \(P\) 是复数集的非空子集，如果 \(P\) 中任意两个数的和、差、积仍属于 \(P\)，则称 \(P\) 是一个数环。即数环对前三则基本运算封闭。

例如全体整数的集合 \(Z\)，全体有理数的集合 \(Q\)，全体实数的集合 \(R\) 和全体复数的集合 \(C\)，分别称为整数环、有理数环、实数环和复数环；对数的加法、乘法均构成环；偶数集是数环，称为偶数环；还有各种代数整数环等。

数域
设 \(P\) 是由一些复数组成的集合，其中包括 0 与 1，如果 \(P\) 中任意两个数的和、差、积、商（除数不为 \(0\)）仍属于 \(P\)，则称 \(P\) 为一个数域。例如复数域 \(\mathbf{C}\)，实数域 \(\mathbf{R}\)，有理数域 \(\mathbf{Q}\)。

特别的：

1. \(z = \{ 0 \}\) 是最小的数环，数环必定含有 0；
2. 有理数集 \(\mathbf{Q}\) 是最小的数域，数域必定含有 0 和 1；

线性空间
设 \(V\) 为定义了加法和数乘运算的非空集合，\(P\) 为一个数域，如果 \(\forall \alpha, \beta, \gamma \in V, k, l \in P\)，集合 \(V\) 均满足：

1. 加法交换律：\(\alpha + \beta = \beta + \alpha\)
2. 加法结合律：\((\alpha + \beta) + \gamma = \alpha + (\beta + \gamma)\)
3. 唯一零元：\(\alpha + 0 = \alpha\)，任意一个元素加上零元均为其本身（零元并不特指整数 0，取决于线性空间的定义）
4. 唯一负元：\(\alpha + \beta = 0, \beta = -\alpha\)，任意一个元素都存在唯一负元，使二者之和等于零元（而不是整数 0）
5. 唯一单位元：\(\alpha \cdot 1 = \alpha\)，任意一个元素乘以单位元均为其本身（单位元并不特指整数 1，取决于线性空间的定义）
6. 乘法分配律：\((k + l) \alpha = k \alpha + l \alpha\)
7. 乘法分配律：\(k(\alpha + \beta) = k \alpha + k \beta\)
8. 乘法结合律：\(k \cdot (l \cdot \alpha) = k \cdot l \cdot \alpha\)

则称 \(V\) 为数域 \(P\) 上的线性空间。

线性空间的维数与基
在线性空间 \(V\) 中，如果存在 \(n\) 个向量线性无关，而任意 \(n+1\) 个向量均线性相关，则这 \(n\) 个向量为 \(V\) 的一组基底，\(n\) 为线性空间 \(V\) 的维数，记为 \(dim \ V = n\)。

例如复线性空间 \(\mathbf{C}\) 在实数域上是二维的，基为 \(\{1, i\}\)；在复数域上是一维的，基为 \(\{1\}\)。

坐标
设 \(x_1, ..., x_n\) 为线性空间 \(V\)（数域 \(P\) 上）的一组基，则 \(\forall x \in V\)，都有且仅有一组数 \(a_1, ..., a_n \in P\) 使得 \(x = a_1 x_1 + ... + a_n x_n\)，则 \((a_1, ..., a_n)^T\) 称为 \(x\) 在基底 \(x_1, ..., x_n\) 下的坐标。

过渡矩阵
设 \(\alpha = \{ \alpha_1, ..., \alpha_n \}, \beta = \{ \beta_1, ..., \beta_n \}\) 为线性空间 \(V\) 的两组不同基，则存在可逆矩阵 \(P\)，使得基底 \(\alpha\) 过渡到基底 \(\beta\)：

\[\alpha P = \beta \]

维数公式
设 \(V_1, V_2\) 为线性空间 \(V\) 的子空间，分别定义两者的和空间和交空间如下：

1. \(V_1 + V_2 = \{ \alpha = \alpha_1 + \alpha_2 \ | \ \alpha_1 \in V_1, \alpha_2 \in V_2 \}\)
2. \(V_1 \cap V_2 = \{ \alpha \ | \ \alpha \in V_1 \cap V_2\}\)

则有维数公式如下：

\[dim(V_1) + dim(V_2) = dim(V_1 + V_2) + dim(V_1 \cap V_2) \]

1.1.2. 线性子空间

定义
子空间为包含于向量空间内的一个向量空间。它是原向量空间的一个子集，而且本身也满足向量空间的要求。注意其与子集的区别，所有元素都在原空间之内就可称之为子集，但是要满足对线性运算封闭的子集才能成为子空间。

张成子空间
设 \(\alpha_1, ..., \alpha_n\) 为线性空间 \(V\) 的一组向量（不一定是基，也可能线性相关），则这组向量的所有可能的线性组合行成的集合，被称为 \(\{\alpha_1, ..., \alpha_n\}\) 的张成子空间，记作 \(span \{ \alpha_1, ..., \alpha_n \} = \{ k_1 \alpha_1 + ... + k_n \alpha_n \}\)，其中 \(k_i \in P\)。

直和
设 \(V_1, V_2\) 为线性空间 \(V\) 的子空间，且 \(\forall \alpha \in V_1 + V_2\)，下面的表示方式有且仅有一种，则称 \(V_1 + V_2\) 为直和，记作 \(V_1 \oplus V_2\)：

\[\alpha = \alpha_1 + \alpha_2, \forall \alpha_1 \in V_1, \alpha_2 \in V_2 \]

\(V_1 + V_2\) 为直和，等价于：

1. \(V_1 \cap V_2\) 为零子空间 \(\{0\}\)
2. \(dim(V_1 + V_2) = dim(V_1) + dim(V_2)\)
3. \(V_1\) 的基和 \(V_2\) 的基，放在一起就是 \(V\) 的基

不变子空间
设 \(T\) 为 线性空间 \(V\) 的线性变换，\(V_1\) 为 \(V\) 的子空间，如果 \(\forall \alpha \in V_1\) 都有 \(T \alpha \in V_1\)，则称 \(V_1\) 为 \(V\) 的不变子空间。

空间正交
设 \(V_1, V_2\) 为线性空间 \(V\) 的子空间，如果 \(\forall \alpha \in V_1, \beta \in V_2\) 都有 \(\alpha \bot \beta\)，则称 \(V_1\) 与 \(V_2\) 相互正交，记为 \(V_1 \bot V_2\)。

特别的，如果 \(V_1 \bot V_2\)，则有 \(V_1 + V_2 = V_1 \oplus V_2\)，即 \(V_1 \cap V_2 = \{0\}\)，两个正交空间的交集只有一个零元素。

正交补
设 \(V_1, V_2\) 为线性空间 \(V\) 的子空间，如果 \(V_1 \bot V_2\) 且 \(V_1 \oplus V_2\)，则称 \(V_1, V_2\) 互为正交补，记作 \(V_1 = V_2^{\perp}, V_2 = V_1^{\perp}\)。

特别的，线性空间 \(V = V_1 \oplus V_1^\perp = V_2 \oplus V_2^\perp\) 称为 \(V\) 的正交直和分解。

1.2. 线性变换

1.2.1. 线性变换

定义
设 \(V_1, V_2\) 为数域 \(P\) 上的两个线性空间，\(f\) 为 \(V_1 \rightarrow V_2\) 的映射，对于 \(\alpha, \beta \in V_1, k \in P\)，如果满足线性的两个条件：

1. 可加性：\(f(\alpha + \beta) = f(\alpha) + f(\beta)\)
2. 齐次性：\(f(k \alpha) = k f(\alpha)\)

则称 \(f\) 为 \(V_1 \rightarrow V_2\) 的线性变换或线性算子（后面一般不用符号 \(f\)，而是符号 \(T\)）。

线性变换的矩阵表示
设 \(T: V^n \rightarrow V^m\) 为线性变换，\(\alpha = \{\alpha_1, ..., \alpha_n \}, \beta = \{ \beta_1, ..., \beta_m\}\) 分别是两个空间的基，则有：

\[T(\alpha) = T(\alpha_1 \ \alpha_2 \ ... \ \alpha_n) = (\beta_1 \ \beta_2 \ ... \ \beta_m)\begin{bmatrix}a_{11} & ... & a_{1n} \\ ... & ... & ... \\ a_{m1} & ... & a_{mn} \end{bmatrix} = \beta A \]

则矩阵 \(A\) 称为线性变换 \(T\) 在基偶 \(\{\alpha, \beta\}\) 下的矩阵。当 \(m=n\) 时，两个线性空间可以使用相同的基，此时\(A\) 为方阵，简称为 \(T\) 在基 \(\alpha\) 下的矩阵。

1.2.2. 零空间与列空间

零空间（化零空间、核空间）
矩阵 \(A\) 的零空间 \(N(A)\) 是满足 \(Ax = 0\) 的所有 \(x\) 的集合。即对于 \(A \in \mathbf{C}^{m \times n}\)，有：

\[N(A) = \{x \ | \ \forall x \in \mathbf{C}^n, Ax = 0\} \]

求解 \(A x = 0\) 的问题，比如 \(A \in \mathbf{C}^{4 \times 3}, rank \ A = 2\)，则 \(N(A)\) 应该是 \(\mathbf{R}^3\) 内的一个子空间。

列空间（值空间）
矩阵 \(A\) 的列空间 \(R(A)\) 是其列向量的所有线性组合所构成的空间。即对于 \(A \in \mathbf{C}^{m \times n}\)，有：

\[R(A) = \{Ax \ | \ \forall x \in \mathbf{C}^n\} \]

求解 \(A x = b\) 的问题，对于给定的矩阵 \(A\)，显然不是任意的 \(b\) 都一定能得到解。比如上例中的矩阵 \(A\)，它的值空间即为两个无关列向量的张成空间，即 \(R(A)\) 为 \(\mathbf{R}^4\) 内的一个二维子空间。

设矩阵 \(A \in \mathbf{C}^{m \times n}\)，关于零空间和列空间，有如下推论：

1. \(R(A) \bot N(A^H)\)
2. \(N(A) \bot R(A^H)\)
3. \(dim R(A) + dim N(A^H) = m\)
4. \(dim R(A^H) + dim N(A) = n\)
5. \(\mathbf{C}^m = R(A) \oplus N(A^H)\)
6. \(\mathbf{C}^n = R(A^H) \oplus N(A)\)

1.2.3. Householder 变换

对向量 \(x \in \mathbf{C}^n\) 进行 Householder 变换使之与标准单位向量 \(e_i \in \mathbf{C}^n\)（第 i 行为 1，其余行为 0）同向：

1. 计算 \(a = \Vert x \Vert_2\)
2. 计算向量 \(u = \frac{x - a e_1}{\Vert x - a e_1 \Vert_2}\)
3. 计算矩阵 \(H = I_n - 2 u u^H\)
4. 则有 \(H x = k e_1\)

1.2.4. Givens 变换

1.3. 内积空间

1.3.1. 欧式空间

设 \(V\) 是 \(n\) 维实线性空间，如果 \(\forall \alpha, \beta \in V\)，都有一个实数与二者相对应（所以也可以理解为一种映射），将该实数记为 \(<\alpha, \beta>\)，如果其满足如下性质：

1. 对称性：\(<\alpha, \beta> = <\beta, \alpha>\)
2. 可加性：\(<\alpha + \beta, \gamma> = <\alpha + \gamma, \beta + \gamma>, \gamma \in V\)
3. 齐次性：\(<k \alpha, \beta> = k <\beta, \alpha>, k \in \mathbf{R}\)
4. 正定性：\(<\alpha, \alpha> \ge 0\)，且等号成立当且仅当 \(\alpha = 0\)

则称 \(<\alpha, \beta>\) 为这两个向量的内积，定义了内积的实线性空间称为欧式空间。

1.3.2. 酉空间

设 \(V\) 是 \(n\) 维复线性空间，如果 \(\forall \alpha, \beta \in V\)，都有一个复数与二者相对应，将该复数记为 \(<\alpha, \beta>\)，如果其满足如下性质：

1. 共轭对称性：\(<\alpha, \beta> = \overline{<\beta, \alpha>}\)，上横线表示共轭
2. 可加性：\(<\alpha + \beta, \gamma> = <\alpha + \gamma, \beta + \gamma>, \gamma \in V\)
3. 齐次性：\(<k \alpha, \beta> = k <\beta, \alpha>, k \in \mathbf{C}\)
4. 正定性：\(<\alpha, \alpha> \ge 0\)，且等号成立当且仅当 \(\alpha = 0\)

则称 \(<\alpha, \beta>\) 为这两个向量的内积，定义了内积的复线性空间称为酉空间。

1.3.3. Schmidt 正交化

以向量组 \(\{\alpha_1, \alpha_2, \alpha_3 \}\) 为例，对其进行施密特正交化得到标准正交基 \(\{\gamma_1, \gamma_2, \gamma_3\}\)：

\[\begin{align*} & \beta_1 = \alpha_1 \\ & \beta_2 = \alpha_2 - <\alpha_2, \gamma_1> \gamma_1 \\ & \beta_3 = \alpha_3 - <\alpha_3, \gamma_2> \gamma_2 - <\alpha_3, \gamma_1> \gamma_1 \\ & \gamma_i = \frac{\beta_i}{| \beta_i |}, i = 1, 2, 3 \end{align*} \]

1.4. 特殊矩阵及性质

1.4.1. 共轭转置矩阵

对矩阵 \(A\) 中的每个元素取共轭复数，再将该矩阵转置，得到的矩阵就是共轭转置矩阵，记作 \(A^H\)。

1.4.2. Hermite 矩阵

设矩阵 \(A \in \mathbf{C}^{n \times n}\)，如果其满足如下条件，则称为自共轭矩阵，又叫 Hermite 矩阵、埃尔米特矩阵、厄米特矩阵（对应实矩阵中的实对称矩阵）：

\[A = A^H \]

比如：

\[A = \begin{bmatrix} 1 & 1+2i \\ 1-2i & -1 \end{bmatrix} \]

关于构造 Hermite 矩阵的两个手法：

1. Hermite 矩阵：\(B = \frac{A + A^H}{2}\)
2. 反 Hermite 矩阵（共轭转置加负号）：\(D = \frac{A - A^H}{2}\)

显然有 \(B + D = A\)，即任意方阵都可以表示为 Hermite 矩阵和反 Hermite 矩阵的和。特别的，Hermite 矩阵的特征值都是实数，反 Hermite 矩阵的特征值都是纯虚数或零（不包含实部）。

1.4.3. 酉矩阵

当矩阵 \(A\) 的逆矩阵为其共轭转置 \(A^H\)时，即如下等式成立时，称矩阵 \(A\) 为酉矩阵（对应实矩阵中的正交矩阵）：

\[A A^H = A^H A = I_n \]

酉矩阵的性质：

1. \(\Vert Ax \Vert = \Vert x \Vert\)
2. 酉矩阵的乘积仍为酉矩阵
3. 酉矩阵特征值的模均为 1（如果是实数，绝对值为 1；如果是虚数，则 \(\sqrt{a^2 + b^2} = 1\)）。

1.4.4. \(\lambda\) 矩阵

矩阵中的每一项都是关于 \(\lambda\) 的多项式，即形如：

\[A = \begin{bmatrix} a_{11}(\lambda) & ... & a_{1n}(\lambda) \\ ... & ... & ... \\ a_{m1}(\lambda) & ... & a_{mn}(\lambda) \end{bmatrix} \]

的矩阵被称为 \(\lambda\) 矩阵（也叫多项式矩阵），比如线代中的特征多项式矩阵 \(\lambda I - A\)。

1.4.5. 矩阵的谱半径

设 \(A \in \mathbf{C}^{n \times n}\)，记 \(\rho(A) = \max\limits_i \ | \lambda_i |\) 为方阵 \(A\) 的谱半径，即最大的特征值绝对值。

1.4.5. 矩阵的奇异值

设 \(A \in \mathbf{C}^{m \times n}, rank \ A = r\)，则矩阵 \(A^H A\) 的特征值 \(\lambda_1 \ge \lambda_2 \ge ... \ge \lambda_r > \lambda_{r+1} = ... = \lambda_n = 0\) 非负。取 \(\sigma_i = \sqrt{\lambda_i}, i = 1, ..., r\) 为矩阵 \(A\) 的正奇异值（其余均为 0）。显然 \(A\) 和 \(A^H\) 的奇异值相同。

1.4.6. 单纯矩阵

一个特征值的代数重数就是它在特征多项式中作为根出现的次数，几何重数就是它对应的特征空间的维数。对于任意矩阵的特征值，其几何重数都小于等于代数重数。如果矩阵每个特征值的几何重数与代数重数都相等，则称该矩阵为单纯矩阵。

一个矩阵是单纯矩阵的充要条件，就是其与对角阵相似。

1.4.7. 正规矩阵

如果矩阵 \(A \in \mathbf{C}^{n \times n}\) 满足 \(A A^H = A^H A\)，则称 \(A\) 为正规矩阵，正规矩阵不一定是 Hermite 矩阵。

如果矩阵 \(A \in \mathbf{R}^{n \times n}\) 满足 \(A A^T = A^T A\)，则称 \(A\) 为实正规矩阵，实正规矩阵不一定是实对称矩阵。

正规矩阵的性质，如果 \(A \in \mathbf{C}^{n \times n}\) 是正规矩阵：

1. 存在酉矩阵 \(U\)，使得 \(U^H A U\)（\(U^H A^H U\)）为对角阵，且对角线元素为 \(A\) 的特征值（的共轭）
2. \(A\) 是单纯矩阵
3. 若 \(A x = \lambda_i x, x \ne 0\)，则 \(A^H x = \overline{\lambda_i} x\)

1.5. Jordan 标准型

1.5.1. Jordan 矩阵

Jordan 块
形如下面的方阵（主对角线相同，主对角线的上一个元素都是 1，其余所有元素均为 0）被称为 Jordan 块，其中 \(\lambda \in \mathbf{C}\)：

\[J = \begin{bmatrix} \lambda & 1 & 0 & ... & 0 \\ 0 & \lambda & 1 & ... & 0 \\ ... & ... & ... & ... & ... \\ 0 & 0 & ... & \lambda & 1 \\ 0 & 0 & 0 & ... & \lambda \end{bmatrix} \]

子 Jordan 矩阵
由多个 \(\lambda\) 相同的 Jordan 块组成的矩阵，形如：

\[\begin{bmatrix} J_1(\lambda) & 0 & ... & 0 \\ 0 & J_2(\lambda) & ... & 0 \\ ... & ... & ... & ... \\ 0 & 0 & ... & J_s(\lambda) \end{bmatrix} \]

Jordan 矩阵
由多个子 Jordan 矩阵组成的矩阵，形如：

\[\begin{bmatrix} J_1(\lambda_1) & 0 & ... & 0 \\ 0 & J_2(\lambda_2) & ... & 0 \\ ... & ... & ... & ... \\ 0 & 0 & ... & J_s(\lambda_s) \end{bmatrix} \]

从定义可以看出，Jordan 矩阵可以划分为多个 \(\lambda\) 不同的子 Jordan 矩阵，每个子 Jordan 矩阵又包含多个 \(\lambda\) 相同的 Jordan 块。

1.5.2. Jordan 标准型

定义
如果 \(n\) 阶方阵 \(A\) 相似于 Jordan 矩阵 \(J\)，即存在 \(n\) 阶可逆矩阵 \(P\)，使得：

\[J = P^{-1} A P \]

则称 \(J\) 为矩阵 \(A\) 的 Jordan 标准型，称 \(P\) 为相似变换矩阵。

行列式因子
设 \(n\) 阶方阵 \(A\) 的特征矩阵 \(A(\lambda) = \lambda I - A\)，所有非零的 \(k = 1, 2, ..., n\) 阶子式的首项系数为 1 的最大公因式称为 \(A\) 的 \(k\) 阶行列式因子，记为 \(D_k(\lambda)\)。

例如：

\[A(\lambda) = \begin{bmatrix} \lambda - 2 & -1 & 0 & 0 \\ 0 & \lambda - 2 & -1 & 0 \\ 0 & 0 & \lambda - 2 & -1 \\ 0 & 0 & 0 & \lambda - 2 \end{bmatrix} \]

1. 非零一阶子式：\(-1, \lambda - 2\)，\(D_1(\lambda) = 1\)
2. 非零二阶子式：\(-1, (\lambda - 2)^2\)，\(D_2(\lambda) = 1\)
3. 非零三阶子式：\(-1, (\lambda - 2)^3\)，\(D_3(\lambda) = 1\)
4. 非零四阶子式：\((\lambda - 2)^4\)，\(D_4(\lambda) = (\lambda - 2)^4\)

不变因子
设 \(D_k(\lambda)\) 为 \(A\) 的各阶行列式因子，令 \(d_i(\lambda)\) 为 \(A\) 的不变因子：

\[d_1(\lambda) = D_1(\lambda), d_2(\lambda) = \frac{D_2(\lambda)}{D_2(\lambda)}, ..., d_n(\lambda) = \frac{D_n(\lambda)}{D_{n-1}(\lambda)} \]

Smith 标准型

通过初等行（列）变换，规则如下：

1. 交换两行或两列
2. 非零数乘某行或某列
3. 某行或某列的 \(\phi(\lambda)\) 倍加到另一行或列

将 \(\lambda\) 矩阵化为如下对角阵，其中 \(rank \ A = r\)，\(d_i(\lambda)\) 为首项系数为 1 的 \(\lambda\) 多项式：

\[A(\lambda) \rightarrow S(\lambda) = diag(d_1(\lambda), d_2(\lambda), ..., d_r(\lambda), 0, ..., 0) \]

对角线的非零元素，即为 \(A(\lambda)\) 的不变因子。

初等因子
将所有的不变因子，分解为互不相同的一次因式方幂，每个因式都是一个初等因子。

判断矩阵 Jordan 块的数目
通过特征值判断，（代数重数）一重特征值对应一阶 Jordan 块，k 重特征值有多少个无关的特征向量，就有多少个以其为对角元的 Jordan 块。

1.5.3. 求解 Jordan 标准型和变换矩阵

\[\begin{align*} 例：& 求矩阵 \ A \ 的 \ Jordan \ 标准型及变换矩阵 \ P，其中 \ A = \begin{bmatrix} 0 & -4 & 0 \\ 1 & -4 & 0 \\ 1 & -2 & -2 \end{bmatrix} \\ 解：& 1. \ 计算矩阵 \ A \ 的特征值，分析 \ Jordan \ 块数目 \\ & 由 | \lambda I - A | = \left| \begin{matrix} \lambda & 4 & 0 \\ -1 & \lambda + 4 & 0 \\ -1 & 2 & \lambda + 2 \end{matrix} \right| = (\lambda + 2)^3 \\ & 所以矩阵 \ A \ 只有一个特征值 -2，代数重数为 3 \\ & 又因为 rank\ (-2 I - A) = 2，无关特征向量有两个，则 \ A \ 对应的 \ Jordan \ 块应该有两个 \\ & 则 \ A \ 对应的 \ Jordan \ 标准型 \ J = \begin{bmatrix} -2 & 0 & 0 \\ 0 & -2 & 1 \\ 0 & 0 & -2 \end{bmatrix} \\ & \\ & 2. \ 列出相似变换，由于存在可逆矩阵 \ P，使得 \ P^{-1} A P = J \\ & 则有 \ A P = P J \\ & 即 \ A (P_1, P_2, P_3) = (P_1, P_2, P_3) \begin{bmatrix} -2 & 0 & 0 \\ 0 & -2 & 1 \\ 0 & 0 & -2 \end{bmatrix} \\ & 得到方程组 \left\{ \begin{array} \ A P_1 = -2 P_1 \\ A P_2 = -2 P_2 \\ A P_3 = P_2 - 2 P_3 \end{array} \right. \\ & 因此 \ P_1, P_2 \ 为 \ \lambda = -2 \ 的无关特征向量，P_3 \ 可根据关于 \ P_2 \ 的方程解得 \\ & \\ & 3. \ 选择 \ P_1, P_2 \\ & 由 \ (-2I - A) = \begin{bmatrix} -2 & -4 & 0 \\ -1 & 2 & 0 \\ -1 & 2 & 0 \end{bmatrix} = \begin{bmatrix} 1 & -2 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \\ & 得两个无关的特征向量 \alpha_1 = (2, 1, 0)^T，\alpha_2 = (0, 0, 1)^T \\ & 经检验，无论选择哪个作为 \ P_2，都将导致方程组无解 \\ & 令 \ P_1 = \alpha_1，P_2 = k \alpha_1 + l \alpha_2 \\ & \\ & 4. \ 求解 \ P_3 \\ & 令 \ P_3 = (x_1, x_2, x_3)^T，则有 (A+2E) P_3 = P_2 \\ & 即 \ \begin{bmatrix} 2 & -4 & 0 \\ 1 & -2 & 0 \\ 1 & -2 & 0 \end{bmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2k \\ k \\ l \end{pmatrix} \\ & 解得 \left\{ \begin{array} \ x_1 - 2 x_2 = k \\ k = l \end{array} \right. \\ & 取 \ k = 1，则 \ P_2 = (2, 1, 1)^T \\ & 再取 \ x_1 = 1，则 x_2 = 0，x_3 \ 为自由变量 \\ & \\ & 5. \ 得到变换矩阵 \\ & 综上，得到可逆矩阵 P = \begin{bmatrix} 2 & 2 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 0 \end{bmatrix} \\ & 使得 P^{-1} A P = \begin{bmatrix} -2 & 0 & 0 \\ 0 & -2 & 1 \\ 0 & 0 & -2 \end{bmatrix} \end{align*} \]

二、范数

2.1. 向量范数

2.1.1. 定义

向量范数是用来刻画向量大小的一种度量。形如：实数的绝对值、复数的模、三维空间向量的长度等，都是抽象的范数概念的原型。对于任意两个 \(n\) 维向量，我们不能直接去比较它们的大小，因为没有比较规则。通过定义某种向量范数（规则），可以将每个 \(n\) 维向量映射为一个实数，所以也可以将范数理解为一种映射（\(f: \mathbf{C}^n \rightarrow \mathbf{R}\)）。不过范数通常不用 \(f(x)\) 来表示，它有专用符号 \(\Vert · \Vert\)。有些常用的范数，会加上右下角标，这是默认的约定，如向量2-范数（\(\Vert x \Vert_2\)）。

在线性空间 \(\mathbf{C}^n\) 中，定义向量范数需要满足如下三条性质：

1. 非负性：\(\Vert x \Vert \ge 0\)，当且仅当 \(x = 0\) 等号成立，其中 \(x \in \mathbf{C}^n\)
2. 齐次性：\(\Vert \lambda x \Vert = | \lambda | \cdot \Vert x \Vert\)，其中 \(\lambda \in \mathbf{C}\)
3. 三角不等式：\(\Vert x + y \Vert \le \Vert x \Vert + \Vert y \Vert\)，其中 \(x, y \in \mathbf{C}^n\)

如果映射 \(\Vert · \Vert: \mathbf{C}^n \rightarrow \mathbf{R}\) 满足以上三条性质，则该映射称为 \(\mathbf{C}^n\) 中的向量范数。定义了范数的线性空间，称为赋范线性空间。

2.1.2. 常用的向量范数

Hölder 范数（p 范数）

\[\Vert x \Vert_p = (|x_1|^p + |x_2|^p + ... + |x_n|^p)^\frac{1}{p}, p \in [1, +\infty) \]

注意 \(p\) 的范围，当 \(p \in (0, 1)\) 时得到的映射不满足三角不等式，所以不属于范数。

Hölder 不等式
若 \(p, q > 1\)，且 \(\frac{1}{p} + \frac{1}{q} = 1\)，则 \(\forall x, y \in \mathbf{C}^n\) 都有：

\[\big{(} \sum_{i=1}^n | x_i | \cdot | y_i | \big{)} \le \big{(} \sum_{i=1}^n | x_i |^p \big{)}^{1/p} \cdot \big{(} \sum_{i=1}^n | y_i |^q \big{)}^{1/q} \]

向量 1 范数
即 \(p\) 范数中，\(p = 1\) 的情况：

\[\Vert x \Vert_1 = (|x_1| + |x_2| + ... + |x_n|) \]

向量 2 范数
即 \(p\) 范数中，\(p = 2\) 的情况：

\[\Vert x \Vert_2 = (|x_1|^2 + |x_2|^2 + ... + |x_n|^2)^\frac{1}{2} \]

向量无穷范数
即 \(p\) 范数中，\(p \rightarrow +\infty\) 的情况：

\[\Vert x \Vert_\infty = \lim_{p \rightarrow +\infty}(|x_1|^p + |x_2|^p + ... + |x_n|^p)^\frac{1}{p} = \max_{1 \le i \le n} | x_i | \]

从上面可以看出，范数指标越高（一范数、二范数、...、无穷范数），它就越关注向量中的大值而忽略小值。

2.2. 矩阵范数

2.2.1. 定义

设矩阵 \(A, B \in \mathbf{C}^{m \times n}\)，如果映射 \(\Vert · \Vert\) 满足：

1. 非负性：\(\Vert A \Vert \ge 0\)，当且仅当 \(A\) 为零矩阵时等号成立
2. 齐次性：\(\Vert \lambda A \Vert = | \lambda | \cdot \Vert A \Vert\)，其中 \(\lambda \in \mathbf{C}\)
3. 三角不等式：\(\Vert A + B \Vert \le \Vert A \Vert + \Vert B \Vert\)
4. 相容性：\(\Vert A B \Vert \le \Vert A \Vert \cdot \Vert B \Vert\)

满足前三条，则称该映射为 \(\mathbf{C}^{m \times n}\) 上的范数。有些书上定义的矩阵范数是对于 \(n\) 阶方阵的，这种定义往往要求矩阵满足相容性，即上述第四条。

2.2.2. 算子范数

是一类矩阵范数而非一种。设 \(\Vert · \Vert_a\) 为 \(\mathbf{C}^n\) 上的向量范数，\(A \in \mathbf{C}^{n \times n}\)，定义映射 \(\Vert · \Vert_m\) 如下：

\[\Vert A \Vert_m = \sup_{\Vert x \Vert_a = 1} \Vert Ax \Vert_a \]

则该映射称为 \(\mathbf{C}^{n \times n}\) 上，由向量范数 \(\Vert · \Vert_a\) 诱导的算子范数（也叫诱导范数）。算子范数有如下性质：

1. 算子范数是矩阵范数，且必与该向量范数相容，即 \(\Vert A x \Vert_a \le \Vert A \Vert_m \cdot \Vert x \Vert_a\)
2. 相容的矩阵范数（算子范数就属于）满足 \(\Vert A \Vert_m \ge | \lambda_i |\)，其中 \(\lambda_i\) 为 \(A\) 的特征值
3. 设 \(A \in \mathbf{C}^{n \times n}\)，\(\Vert A \Vert_{a}\) 为从属于向量范数 \(\Vert x \Vert_a\) 的算子范数，则当 \(\Vert A \Vert_a < 1\) 时 \(E-A\) 可逆，且 \(\Vert (E-A)^{-1} \Vert_a \le (1 - \Vert A \Vert_a)^{-1}\)

2.2.3. 常用的矩阵范数

矩阵 1 范数

\[\Vert A \Vert_{m_1} = \sum_{j=1}^n \sum_{i=1}^n | a_{ij} | \]

矩阵 2 范数（F-范数）

\[\Vert A \Vert_{m_2} = (\sum_{j=1}^n \sum_{i=1}^n | a_{ij} |^2)^{1/2} \]

F-范数的性质：

1. 记作 \(\Vert A \Vert_{m_2}\) 或者 \(\Vert A \Vert_{F}\)，二者等价
2. \(\Vert A \Vert_{m_2}^2 = tr(A^H A) = \sum_{i=1}^n \lambda_i (A^H A) = \sum_{i=1}^n \lambda_i^2 (A)\)
3. 对于任意酉矩阵 \(U, V\)，均有 \(\Vert U A V \Vert_{m_2} = \Vert U A \Vert_{m_2} = \Vert A V \Vert_{m_2} = \Vert A \Vert_{m_2} = \Vert U^H A V \Vert_{m_2} = \Vert U A V^H \Vert_{m_2}\)
4. 设矩阵 \(A \in \mathbf{C}^{m \times n}, rank \ A = r\) 的正奇异值为 \(\sigma_1, ..., \sigma_r\)，则 \(\Vert A \Vert_{m_2} = (\sum_{i=1}^r \sigma_i^2)^{1/2}\)

矩阵无穷范数

\[\Vert A \Vert_{m_\infty} = \max_{i,j} \ \{ | a_{ij} | \} \]

矩阵的无穷范数与 \(\Vert x \Vert_{\infty}\) 不相容，除这个外，其余几个范数都与对应的向量范数相容。

从属于向量 1 范数的算子范数（列和范数，即最大列和）

\[\Vert A \Vert_{1} = \max_{j} \ ( \sum_{i=1}^n | a_{ij} | ) \]

从属于向量 2 范数的算子范数（谱范数）

\[\Vert A \Vert_{2} = \sqrt{r(A^H A)} \]

谱范数的性质：

1. \(\Vert A \Vert_2 = \Vert A^H \Vert_2 = \Vert A^T \Vert_2 = \Vert \overline{A} \Vert_2\)
2. \(\Vert A^H A \Vert_2 = \Vert A A^H \Vert_2 = \Vert A \Vert_2^2\)
3. 对于任意酉矩阵 \(U, V\)，均有 \(\Vert U A V \Vert_2 = \Vert U A \Vert_2 = \Vert A V \Vert_2 = \Vert A \Vert_2\)
4. \(\Vert A \Vert_2^2 \le \Vert A \Vert_1 \Vert \cdot A \Vert_\infty\)
5. 设矩阵 \(A \in \mathbf{C}^{m \times n}, rank \ A = r\) 的正奇异值为 \(\sigma_1, ..., \sigma_r\)，则 \(\Vert A \Vert_{2} = \max_i \sigma_i\)

从属于向量无穷范数的算子范数（行和范数，即最大行和）

\[\Vert A \Vert_{\infty} = \max_{i} \ ( \sum_{j=1}^n | a_{ij} | ) \]

2.2.4. 酉不变范数

定义

是一类矩阵范数而非一种。设 \(U\) 为任意 \(n\) 阶酉矩阵，\(A \in \mathbf{C}^{m \times n}\)，如果映射 \(\Vert · \Vert: \mathbf{C}^{m \times n} \rightarrow \mathbf{R}\) 满足：

1. 非负性：\(\Vert A \Vert \ge 0\)，当且仅当 \(A\) 为零矩阵时等号成立
2. 齐次性：\(\Vert \lambda A \Vert = | \lambda | \cdot \Vert A \Vert\)，\(\forall \lambda \in \mathbf{C}\)
3. 三角不等式：\(\Vert A + B \Vert \le \Vert A \Vert + \Vert B \Vert\)，\(\forall A, B \in \mathbf{C}^{m \times n}\)
4. 酉不变性：\(\Vert U A V \Vert = \Vert A \Vert\)，对任意 \(m, n\) 阶酉矩阵 \(U, V\) 均成立
5. 如果 \(rank \ A = 1\)，则 \(\Vert U A V \Vert = \Vert A \Vert_2\)，即酉不变范数等于谱范数

常见范数分类

1. \(\Vert A \Vert_2\)（谱范数）是酉不变范数
2. \(\Vert A \Vert_{m_2} \Leftrightarrow \Vert A \Vert_F\)（F 范数）是酉不变范数
3. \(\Vert A \Vert_1, \Vert A \Vert_{\infty}\) 不是酉不变范数

三、矩阵分解

3.1. 三角分解

矩阵的三角分解，将矩阵分解为一个酉矩阵（或者正交矩阵，如果是实矩阵分解的话）和一个三角矩阵的乘积

3.1.1. LR 分解

若矩阵 \(A\) 为满秩复方阵，则可唯一分解为：

1. \(A = LR\)，其中 \(L\) 是单位下三角复矩阵，\(R\) 是上三角复矩阵
2. \(A = LR\)，其中 \(L\) 是下三角复矩阵，\(R\) 是单位上三角复矩阵
3. \(A = LDR\)，其中 \(L\) 是单位下三角复矩阵，\(R\) 是单位上三角复矩阵，\(D\) 是对角矩阵

\[\begin{align*} 例：& 利用待定系数法对矩阵 A 做 LR 分解，其中 A = \begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & 3 \\ 0 & -6 & 0 \end{bmatrix} \\ 解：& 令 \ A = LR = \begin{bmatrix} 1 & 0 & 0 \\ ? & 1 & 0 \\ ? & ? & 1 \end{bmatrix} \cdot \begin{bmatrix} ? & ? & ? \\ 0 & ? & ? \\ 0 & 0 & ? \end{bmatrix} \\ & 通过解线性方程，得：\\ & \qquad L = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -3 & 1 \end{bmatrix}，R = \begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & 3 \\ 0 & 0 & 9 \end{bmatrix} \\ & 其中 L 是单位下三角矩阵，R 是上三角矩阵 \\ & 更进一步，可将 R 分成对角阵乘以单位上三角阵 \\ & A = LDR = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -3 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & & \\ & 2 & \\ & & 9 \end{bmatrix} \cdot \begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 3/2 \\ 0 & 0 & 1 \end{bmatrix} \end{align*} \]

特别的：

1. 满秩方阵才有 \(LR\)（以及其它两种）分解式
2. 分解式是唯一的
3. 对正线上（下）三角矩阵施加酉变换（U 矩阵）可以得到满秩矩阵（原矩阵）

3.1.2. QR 分解

若矩阵 \(A\) 为满秩实方阵，则可唯一分解为 \(A = LQ\)，其中 \(L\) 是正线下三角实矩阵，\(Q\) 是正交矩阵。同样的，\(A\) 可唯一分解为 \(A = QR\)，其中 \(R\) 是正线上三角实矩阵，\(Q\) 是正交矩阵。

\[\begin{align*} 例：& 利用 Schmidt 正交化对矩阵 A 做 QR 分解，其中 A = \begin{bmatrix} 0 & 4 & 1 \\ 1 & 1 & 1 \\ 0 & 3 & 2 \end{bmatrix} \\ 解：& 经验证，矩阵 A 可逆，令 A = (\alpha_1, \alpha_2, \alpha_3) \\ & 取 \ \beta_1 = \alpha_1 \\ & \beta_2 = \alpha_2 - <\alpha_2, \beta_1> \beta_1 \\ & \beta_3 = \alpha_3 - <\alpha_3, \beta_2> \beta_2 - <\alpha_3, \beta_1> \beta_1 \\ & 取 \ \gamma_i = \frac{\beta_i}{\Vert \beta_i \Vert_2} \\ & 则 \ A = \begin{pmatrix} \gamma_1 & \gamma_2 & \gamma_3 \end{pmatrix} \cdot \begin{bmatrix} \Vert \beta_1 \Vert_2 & <\alpha_2, \gamma_1> & <\alpha_3, \gamma_1> \\ & \Vert \beta_2 \Vert_2 & <\alpha_3, \gamma_2> \\ & & \Vert \beta_3 \Vert_2 \end{bmatrix} = QR \\ & 其中 \ Q \ 为正交阵，R \ 为正线上三角实矩阵 \end{align*} \]

3.2. 谱分解

3.2.1. 单纯矩阵的谱分解

设 \(A \in \mathbf{C}^{n \times n}\) 为单纯矩阵，则 \(A\) 可分解为一系列幂等矩阵的加权和（\(\lambda_i\) 为 \(A\) 的特征值），即：

\[A = \sum_{i=1}^n \lambda_i A_i \]

\[f(A) = \sum_{i=1}^n f(\lambda_i) A_i \]

其推导过程如下：

\[\begin{align*} A & = P \cdot diag(\lambda_1, ..., \lambda_n) \cdot P^{-1} \\ & = \begin{bmatrix} \alpha_1 & \alpha_2 & ... & \alpha_n \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & ... & 0 \\ 0 & \lambda_2 & ... & 0 \\ ... & ... & ... & ... \\ 0 & 0 & ... & \lambda_n \end{bmatrix} \begin{bmatrix} \beta_1 \\ \beta_2 \\ ... \\ \beta_n \end{bmatrix} \\ & = \sum_{i=1}^n \lambda_i \alpha_i \beta_i \\ 由 \ & P P^{-1} = I \ 得 \ \beta_i \cdot \alpha_i = 1，即 \ A_i \cdot A_i = A_i，所以其为幂等阵 \end{align*} \]

3.2.1. 正规矩阵的谱分解

Schur 引理
设 \(A \in \mathbf{C}^{n \times n}\)，则存在酉矩阵 \(U\)，使得 \(A = U R U^H\)，其中 \(R\) 为上三角矩阵，且主对角线元素为 \(A\) 的特征值。

正规矩阵的谱分解
设 \(A \in \mathbf{C}^{n \times n}\) 为正规矩阵，则存在酉矩阵 \(U\)，使得：

\[A = U \cdot diag(\lambda_1, ..., \lambda_n) \cdot U^H \]

特别的，\(A\) 可酉相似对角化，是 \(A\) 为正规矩阵的充要条件。

3.3. 奇异值分解

设矩阵 \(A \in \mathbf{C}^{m \times n}_r\)（下标为矩阵的秩），\(\sigma_1, ..., \sigma_r\) 为其 r 个正奇异值，则存在酉矩阵 \(U \in \mathbf{C}^{m \times m}, V \in \mathbf{C}^{n \times n}\) 以及矩阵 \(\Sigma \in \mathbf{C}^{m \times n}\)，使得：

\[\begin{align*} A & = U \Sigma V^H \\ & = \begin{bmatrix} U_1 & U_2\end{bmatrix} \begin{bmatrix} diag(\sigma_1, ..., \sigma_r) & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} \end{align*} \]

其中 \(V\) 为 \(A^H A\) 的单位正交的特征向量矩阵，\(V_1\) 为 \(V\) 的前 r 列，\(V_1\) 为 \(V\) 的剩余列。\(U_1 = A V_1 \Sigma^{-1}\)，\(U_2\) 为构造矩阵，其每一列都与 \(U_1\) 中的任一列向量正交。

\[\begin{align*} 例：& 求矩阵 \ A \ 的奇异值分解，其中 \ A = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix} \\ 解：& 1. \ 计算矩阵 \ A \ 的奇异值及 \ \Sigma \ 矩阵 \\ & A^H A = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 2 \end{bmatrix} \\ & | \lambda I - A^H A | = \left| \begin{matrix} \lambda - 1 & 0 & -1 \\ 0 & \lambda - 1 & -1 \\ -1 & -1 & \lambda - 2 \end{matrix} \right| = \lambda (\lambda - 1) (\lambda - 3) \\ & 所以矩阵 \ A \ 的特征值为：\lambda_1 = 3, \lambda_2 = 1, \lambda_3 = 0 \\ & 所以矩阵 \ A \ 的正奇异值为：\sigma_1 = \sqrt{3}, \sigma_2 = 1 \\ & 将正奇异值按照从大到小的顺序排列在对角线上，则有 \ \Sigma = \begin{bmatrix} \sqrt{3} & 0 \\ 0 & 1 \end{bmatrix}，\Sigma^{-1} = \begin{bmatrix} \frac{1}{\sqrt{3}} & 0 \\ 0 & 1 \end{bmatrix} \\ & \\ & 2. \ 通过 \ A^H A \ 的特征向量，计算 \ V \ 矩阵 \\ & \lambda_1 = 3, \lambda_2 = 1, \lambda_3 = 0 对应的特征向量分别为：\alpha_1 = \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix}，\alpha_2 = \begin{bmatrix} 1 \\ -1 \\ 0 \end{bmatrix}，\alpha_3 = \begin{bmatrix} 1 \\ 1 \\ -1 \end{bmatrix} \\ & 由于三个向量属于不同特征值，无需正交化，只对其进行单位化 \\ & 即得：\gamma_1 = \frac{1}{\sqrt{6}} \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix}，\gamma_2 = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ -1 \\ 0 \end{bmatrix}，\gamma_3 = \frac{1}{\sqrt{3}} \begin{bmatrix} 1 \\ 1 \\ -1 \end{bmatrix} \\ & 则得到矩阵 \ V = \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{2}{\sqrt{6}} & 0 & -\frac{1}{\sqrt{3}} \end{bmatrix} \\ & \\ & 3. \ 计算 \ U \ 矩阵 \\ & 则有 \ U_1 = A V_1 \Sigma^{-1} = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} \\ \frac{2}{\sqrt{6}} & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{3}} & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ 0 & 0 \end{bmatrix} \\ & 构造 \ U_2 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}，其每一列均与 \ U_1 \ 的任意列向量均正交 \\ & 则有 \ U = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & \\ & 4. \ 写出奇异值分解式 \\ & 对 \ \Sigma 进行扩充，得到 \ \Sigma = \begin{bmatrix} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} \\ & 则有 \ A = U \Sigma V^H = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{3}} \end{bmatrix} \end{align*} \]

3.4. 满秩分解

设矩阵 \(A \in \mathbf{C}^{m \times n}_r\)，则存在矩阵 \(B \in \mathbf{C}^{m \times r}, D \in \mathbf{C}^{r \times n}\) 使得：

\[A = B D \]

其中矩阵 \(D\) 为原矩阵行最简形式的前 r 行，矩阵 \(B\) 为原矩阵行最简形式中，组成单位阵 \(E_r\) 的列号，在原矩阵中对应的列。

\[\begin{align*} 例：& 求矩阵 \ A \ 的满秩分解，其中 \ A = \begin{bmatrix} 1 & 4 & 1 & 11 & -7 \\ 2 & 1 & -1 & -3 & 0 \\ 1 & 0 & -3 & -1 & 1 \\ 0 & 2 & -6 & 14 & -4 \end{bmatrix} \\ 解：& 1. \ 将矩阵 \ A \ 化为行最简形式 \\ & 得 \ A \rightarrow \begin{bmatrix} 1 & 0 & 0 & -4 & 1 \\ 0 & 1 & 0 & 4 & -2 \\ 0 & 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}，rank \ A = 3 \\ & \\ & 2. \ 取矩阵 \ D \ 为 \ A \ 行最简形式的前 r 行 \\ & 则 \ D = \begin{bmatrix} 1 & 0 & 0 & -4 & 1 \\ 0 & 1 & 0 & 4 & -2 \\ 0 & 0 & 1 & -1 & 0 \end{bmatrix} \\ & \\ & 3. \ 取矩阵 \ B \\ & 在 \ A \ 的行最简形式中找到组成单位阵 \ E_r \ 的列号，本例为第 1, 2, 3 列 \\ & 在矩阵 \ A \ 中取这 \ r \ 列组成矩阵 \ B \\ & 即 \ B = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \\ & \\ & 4. \ 写出满秩分解式 \\ & 则有 A = BD = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -4 & 1 \\ 0 & 1 & 0 & 4 & -2 \\ 0 & 0 & 1 & -1 & 0 \end{bmatrix} \end{align*} \]

四、特征值的估计与摄动

4.1. 特征值界估计

设矩阵 \(A \in \mathbf{C}^{n \times n}\)，令矩阵 \(B = \frac{A + A^H}{2}, C = \frac{A - A^H}{2}\)，则 \(B, C\) 为 Hermite 矩阵（特征值均为实数）和反 Hermite 矩阵（特征值均为纯虚数）。令 \(A, B, C\) 的特征值集合为 \(\{\lambda_1, ..., \lambda_n \}, \{\mu_1, ..., \mu_n \}, \{i\gamma_1, ..., i\gamma_n \}\)，且均按照由大到小的顺序排序。

令 \(Re(\lambda_i)\) 表示 \(\lambda_i\) 的实部，\(Im(\lambda_i)\) 表示 \(\lambda_i\) 的虚部。

Schur 不等式（舒尔）
设矩阵 \(A \in \mathbf{C}^{n \times n}\) 的特征值为 \(\lambda_1, ..., \lambda_n\)。则有关于特征值的范围的不等式：

\[\sum_{i=1}^n \lambda_i^2 \le \sum_{i=1}^n \sum_{j=1}^n a_{ij}^2 = \Vert A \Vert_F^2 \]

等号成立，当且仅当 \(A\) 为正规矩阵，即 \(A A^H = A^H A\)。

Hadamard 不等式（哈达玛）
设矩阵 \(A \in \mathbf{C}^{n \times n} = (\alpha_1, ..., \alpha_n)\) 的特征值为 \(\lambda_1, ..., \lambda_n\)，则有关于行列式的范围的不等式：

\[\prod_{i=1}^n | \lambda_i | = | det \ A | \le \Vert \alpha_1 \Vert_2 \cdot ... \cdot \Vert \alpha_n \Vert_2 \]

等号成立，当且仅当 \(A\) 的某一列全为零元。

定理

\[\mu_n \le Re(\lambda_i) \le \mu_1 \]

\[\gamma_n \le Im(\lambda_i) \le \gamma_1 \]

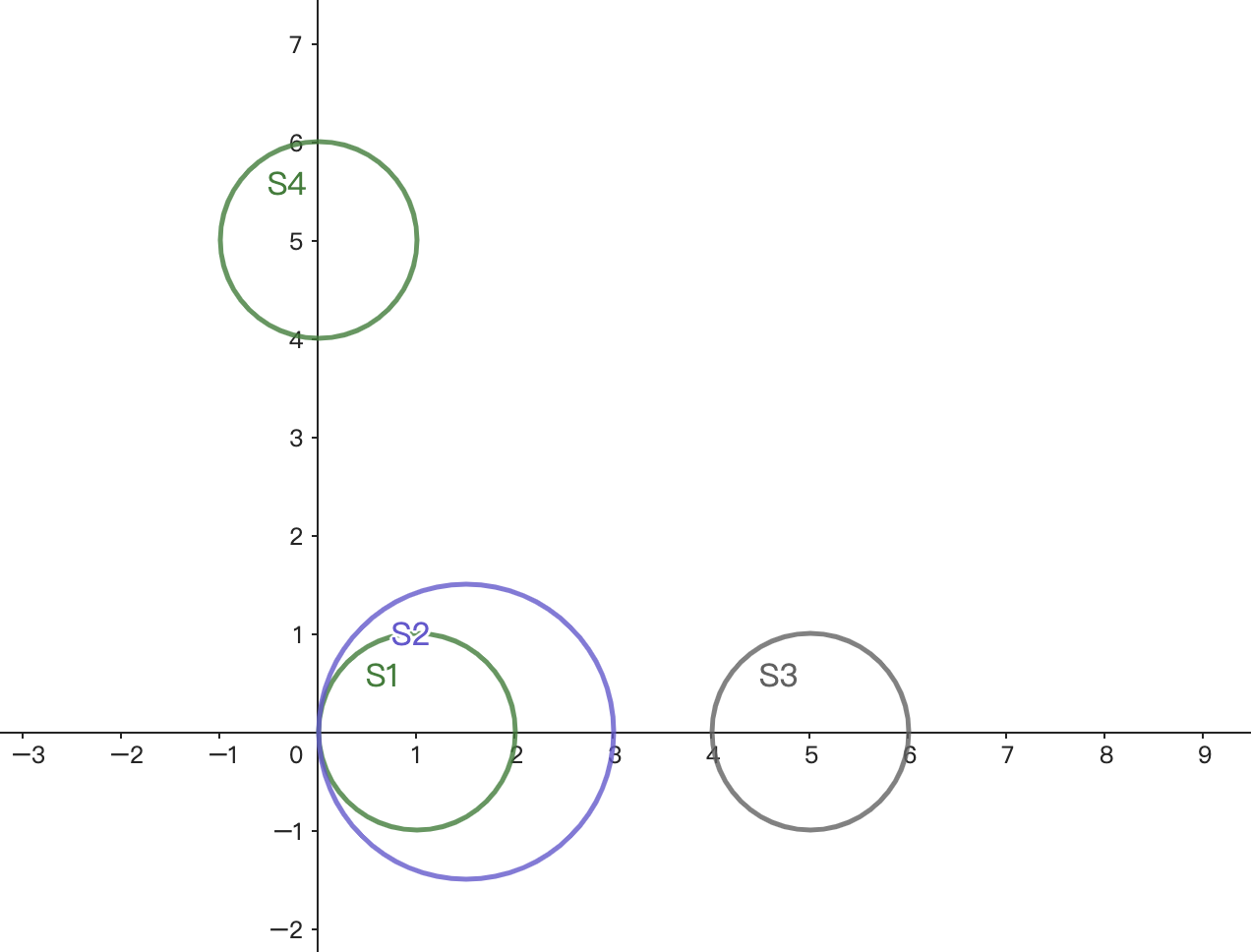
4.2. 盖尔圆盘定理

盖尔圆

1. 行盖尔圆：\(S_i = \{ z \in \mathbf{C} \ | \ | z - a_{ii} | \le R_i = \sum_{j \ne i} |a_{ij}| \}\)
2. 列盖尔圆：\(G_j = \{ z \in \mathbf{C} \ | \ | z - a_{jj} | \le C_j = \sum_{i \ne j} |a_{ij}| \}\)

通俗的说：

1. \(S_i\) 表示第 \(i\) 行对应的行盖尔圆，是一个点集，集合中每个元素距离圆心（该行对角元）的距离，不超过 \(R_i\)（去掉该行对角元的所有元素绝对值的和）。
2. \(G_j\) 表示第 \(j\) 列对应的列盖尔圆，是一个点集，集合中每个元素距离圆心（该列对角元）的距离，不超过 \(C_j\)（去掉该列对角元的所有元素绝对值的和）。

盖尔圆盘定理
设矩阵 \(A \in \mathbf{C}^{n \times n}\)，则其任一特征值均满足：

\[\lambda_i \in \bigcup_{j=1}^n S_j, i = 1, ..., n \]

也就是说，任意一个特征值，均落在其行盖尔圆的集合内。对列盖尔圆也有相同结论。

盖尔圆盘定理推广
如果 \(n\) 阶方阵的 \(n\) 个行盖尔圆中有 \(k\) 个盖尔圆的并集形成一个连通区域（只要存在一个交点就算），则在这个连通区域中恰有 \(k\) 个特征值。对列盖尔圆也有相同结论。

\[\begin{align*} 例：& 求矩阵 \ A \ 的盖尔圆，其中 \ A = \begin{bmatrix} 1 & -1/2 & -1/2 & 0 \\ -1/2 & 2/3 & i & 0 \\ 0 & -i/2 & 5 & i/2 \\ -1 & 0 & 0 & 5i \end{bmatrix}。\\ 解：& \ A \ 的四个盖尔圆分别为：\\ & S_1: \{ z \in \mathbf{C} \ | \ \left| z - 1 \right| \le R_1 = 1 \}，其中 R_1 = \left| -\frac{1}{2} \right| + \left| -\frac{1}{2} \right| + \left| 0 \right| = 1 \\ & S_2: \{ z \in \mathbf{C} \ | \ \left| z - \frac{3}{2} \right| \le R_2 = \frac{3}{2} \}，其中 R_2 = \left| -\frac{1}{2} \right| + \left| i \right| + \left| 0 \right| = \frac{3}{2} \\ & S_3: \{ z \in \mathbf{C} \ | \ \left| z - 5 \right| \le R_3 = 1 \}，其中 R_3 = \left| 0 \right| + \left| -\frac{i}{2} \right| + \left| \frac{i}{2} \right| = 1 \\ & S_4: \{ z \in \mathbf{C} \ | \ \left| z - 5i \right| \le R_4 = 1 \}，其中 R_4 = \left| -1 \right| + \left| 0 \right| + \left| 0 \right| = 1 \\ & 则 \ A \ 的特征值均落在下图的四个圆内 \\ & 其中 \ S_1, S_2 \ 两个区域重叠，其中包含两个特征值，而 \ S_3, S_4 \ 内各有一个特征值 \end{align*} \]

五、矩阵分析

5.1. 矩阵函数的求法

1. 求出矩阵的 Jordan 标准型及变换矩阵

2. 按照如下公式对每个 Jordan 块 \(J_i\) 计算 \(f(J_i)\)，其中 \(m_i\) 表示该 Jordan 块的阶数

\[f(J_i) = \begin{bmatrix} f(\lambda_i) & \frac{1}{1!} f^{'}(\lambda_i) & ... & \frac{1}{(m_i - 1)!} f^{(m_i-1)}(\lambda_i) \\ & f(\lambda_i) & ... & ... \\ & & ... & \frac{1}{1!} f^{'}(\lambda_i) \\ & & & f(\lambda_i) \end{bmatrix} \]

3. 将 \(f(J_i)\) 按顺序排列，合成 \(f(J)\)

\[f(J) = diag(f(J_1), f(J_2), ..., f(J_s)) \]

4. 按照 \(f(A) = P f(J) P^{-1}\) 计算矩阵函数

\[\begin{align*} 例：& 矩阵 \ A = \begin{bmatrix} 1 & 2 & 3 & 4 \\ & 1 & 2 & 3 \\ & & 1 & 2 \\ & & & 1 \end{bmatrix}，计算 \sqrt{A}。\\ 解：& 1. \ 求出矩阵 \ A \ 的 \ Jordan \ 标准型及变换矩阵 \ P（如果 \ A \ 已经是 \ Jordan \ 标准型则不需要这一步） \\ & J = \begin{bmatrix} 1 & 1 & 0 & 0 \\ & 1 & 1 & 0 \\ & & 1 & 1 \\ & & & 1 \end{bmatrix}，P = \begin{bmatrix} 8 & 4 & 0 & 0 \\ & 4 & -1 & 1 \\ & & 2 & -2 \\ & & & 1 \end{bmatrix}，P^{-1} = \frac{1}{16} \begin{bmatrix} 2 & -2 & -1 & 0 \\ & 4 & 2 & 0 \\ & & 8 & 16 \\ & & & 16 \end{bmatrix} \\ & \\ & 2. \ 求出 \ f(\lambda_i)，f^{'}(\lambda_i)，f^{''}(\lambda_i) ，...，f^{(m_i - 1)}(\lambda_i) \ 并构造 \ f(J_i) \\ & f(J_1) = \begin{bmatrix} f(1) & \frac{1}{1!} f^{'}(1) & ... & \frac{1}{(4- 1)!} f^{(4-1)}(1) \\ & f(1) & ... & ... \\ & & ... & \frac{1}{1!} f^{'}(1) \\ & & & f(1) \end{bmatrix} = \frac{1}{16} \begin{bmatrix} 16 & 8 & -2 & 1 \\ & 16 & 8 & -2 \\ & & 16 & 8 \\ & & & 16 \end{bmatrix} \\ & \\ & 3. \ 合成 \ f(J) \\ & 由于本例矩阵只包含一个 \ Jordan \ 块，所以 \ f(J) = f(J_1) \\ & \\ & 4. \ 计算 \ f(A) \\ & f(A) = P f(J) P^{-1} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ & 1 & 1 & 1 \\ & & 1 & 1 \\ & & & 1 \end{bmatrix} \end{align*} \]

六、广义逆矩阵

6.1. M-P 广义逆矩阵

定义
设矩阵 \(A \in \mathbf{C}^{n \times n}\)，如果存在矩阵 \(G\) 满足：

1. \(AGA = A\)
2. \(GAG = G\)
3. \((GA)^H= GA\)
4. \((AG)^H = AG\)

则称 \(G\) 为 \(A\) 的 M-P 广义逆矩阵，记作 \(A^+\)。

性质

1. \((A^+)^+ = A\)
2. \((A^H)^+ = (A^+)^H\)
3. \(A^+ = (A^H A)^+ A^H = A^H (A^H A)^+\)
4. \(R(A^+) = R(A^H), N(A^+) = N(A^H)\)
5. \((A^H A)^+ = A^+ (A^H)^+\)
6. \((A^2)^+ = (A^+)^2 \Leftrightarrow A\) 为 Hermite 矩阵

通过满秩分解计算
根据矩阵满秩分解，我们有 \(A = BD\)，则矩阵 \(A\) 的 M-P 广义逆矩阵可表示为：

\[A^+ = D^+ B^+ = D^H (D D^H)^{-1} (B^H B)^{-1} B^H \]

方程的解

1. 线性齐次方程组：\(Ax = b\) 有解的充要条件为 \(A A^+ b = b\)，有解时的通解为 \(x = A^+ b +(I_n - A^+ A) y, \forall y \in \mathbf{C}^n\)
2. 最小二乘解：通解形式为 \(x = A^+b +(I_n - A^+ A) y\)
3. 最佳逼近解：\(x = A^+ b\)