004. 节能型MEC系统中的计算和协作通信

一、简介

论文信息

1	2
论文名称	Joint Computation and Communication Cooperation for Energy-Efficient Mobile Edge Computing
出版日期	2018/10/10
发表期刊	IEEE Internet of Things Journal ( Volume: 6, Issue: 3, June 2019)
地址	https://ieeexplore.ieee.org/abstract/document/8488502

总结

本文研究了移动边缘计算（MEC）中计算卸载（Computation Offloading）的优化问题。在边缘网络中如何分配用户设备的计算任务，以使整体耗电量最小？本文针对 User-Helper-AP 三节点模型求解这个问题的最优解。通过构建两个非线性规划问题，分别对可分割任务和不可分割任务的最优耗电量进行建模，并使用拉格朗日乘子法和 KKT 条件等方法求出最优解，以达到节约设备用电的目的。

这篇文章是 LP 问题在 MEC 领域的经典应用。多时隙划分使用，带有 Helper 的三节点 MEC 以及 User 间协作（Helper 就是空闲 User）的设计相较于单纯的 MEC 系统来说确实提高了系统能效和利用率。但不足的是，仿真对比的对象都是没有联合优化的基准方案，而不是其它不同思路的优化方案。且没有配置类似多智能体环境，即多 User 多 Helper，距离实际应用尚有差距。

二、简单译文

Abstract

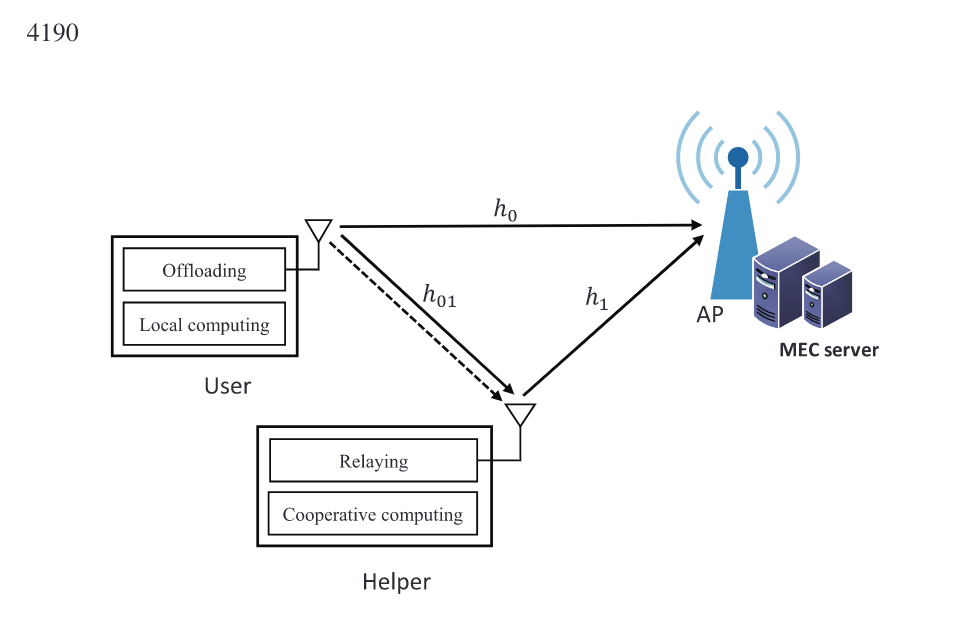
本文提出了一种新的用户协作方法，用于MEC系统中的计算和通信，以提高延迟受限计算（即有延迟限制的计算任务）的能效。考虑一个基本的三节点MEC系统，其包含一个 User 节点、一个 Helper 节点和一个 AP 节点（用于连接MEC服务器）组成。在该系统中，用户需要执行延迟受限的计算密集型任务。考虑两种不同的卸载模型，分别是部分卸载和二元卸载。

1. 部分卸载：用户任务可能分布在这三个节点上执行
2. 二元卸载：用户任务作为一个不可分割的整体在某一个节点上执行

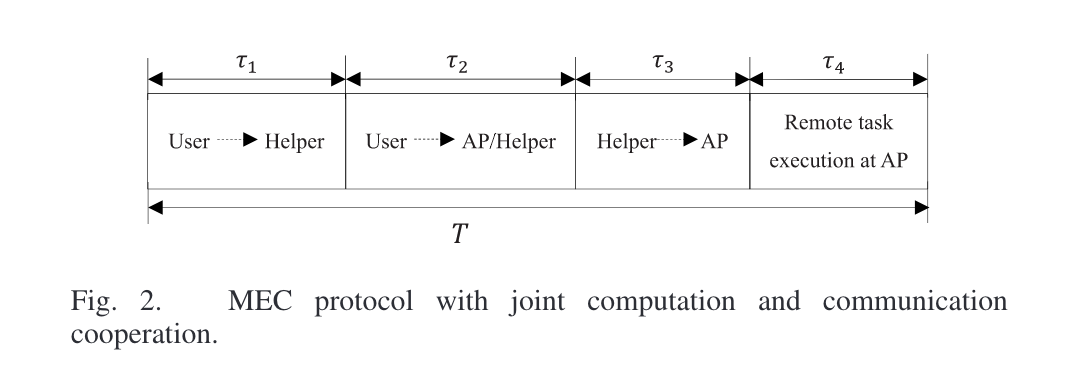
此外，针对特定的时间块，开发一个高效的四时隙传输协议，用于实现联合计算和协作通信：

1. 第一时隙：User 将一些计算任务（\(l_h\)）卸载给 Helper，Helper 在剩余时间（\(T - \tau_1\)）内协同计算这些任务
2. 第二时隙：User 将需要 AP 执行的任务（\(l_a\)）卸载给 AP 或者 Helper（如果需要 Helper 作中继的话）
3. 第三时隙：第二时隙 Helper 作为中继的情况下，Helper 将 User 传输的任务发送给 AP
4. 第四时隙：AP（MEC 服务器）执行第二时隙和第三时隙卸载给自己的任务

对于部分卸载和二元卸载两种情况，我们联合优化了 User 和 Helper 的计算和通信资源分配（即卸载的时间和传输功率分配，以及 CPU 的计算频率），以便在满足用户的计算延迟约束的同时最小化它们的总能耗。尽管这两个问题通常是非凸的，但我们开发了有效的算法来最优地解决它们。

Introduction

最近，第五代（5G）蜂窝技术的进步已经实现了各种新的应用，如增强现实（AR）、自动驾驶和物联网（IoT）。这些应用需要大量无线设备（例如传感器和致动器）之间的超低延迟通信、计算和控制[2]。在实践中，要执行的实时计算任务可能非常密集，但无线设备通常又很小，只支持有限的通信、计算和存储[3]。因此，如何增强其计算能力并降低通信延迟是实现这些 5G 应用的一个关键且具有挑战性的问题。

传统上，移动云计算（MCC）已被广泛采用，通过将无线设备的计算和数据存储移动到云服务器（远程执行）来增强其计算能力。然而，由于云服务器通常远离无线设备，MCC 可能无法满足新兴 5G 应用的低延迟要求。为了克服这些限制，最近提出了移动边缘计算（MEC）作为一种新的解决方案，通过在无线网络边缘（如接入点 AP 和蜂窝基站 BS）部署分布式 MEC 服务器提供云计算[3]–[9]。其中，无线设备可以将计算密集型和延迟关键型任务卸载到 AP/BS，由于 MEC 很近，即使是远程执行也可以实现比 MCC 更低的计算延迟。在二元卸载中，计算任务是不可分割的，这实际上对应那些高度集成或相对简单的任务，如语音识别或自然语言翻译。而部分卸载需要任务可以被分割为多个可独立执行的部分，如 AR 应用。

基于二进制和部分卸载模型，先前的工作[9]-[17]研究了联合计算和通信资源分配，以提高 MEC 的性能。[10]-[11]考虑了具有动态任务到达和信道衰落的单用户 MEC 系统，其中用户联合优化本地计算或卸载决策，以最小化计算延迟，同时受计算和通信资源约束。[12]-[14]研究了多用户 MEC 系统中的节能设计，其中多个用户将各自的任务卸载到单个 AP/BS 执行，其目标是最小化用户能耗，同时确保其计算延迟约束。[15]–[17]通过将新兴的无线电能传输（WPT）技术集成到 MEC 中，提出了无线供电 MEC 系统，以实现自我可持续计算，其中 AP 使用 WPT 为用户的本地计算和卸载提供电力。

尽管最近取一些研究进展，但多用户 MEC 设计仍面临若干技术挑战。首先，MEC 服务器上的计算资源和 AP 上的通信资源应该在活跃用户之间共享。当用户数量变大时，分配给每个用户的计算和通信资源从根本上受到限制。其次，由于信号传播的损失，远距离用户可能会比近距离用户花费更多的通信资源，这会导致公平性问题。请注意，5G 网络由大规模具有一定计算和通信资源的无线设备组成。由于无线通信的突发性，每个活动设备很可能被一些闲置设备所包围，这些闲置设备具有未使用的资源。因此，在本文中，我们提出了一种新的多用户 MEC 系统中的联合计算和通信协作方法，使得附近的用户能够作为 Helper 来共享他们的计算和通信资源，以帮助有计算需求的用户，从而提高 MEC 计算性能。

本文考虑了一个具有用户协作的三节点 MEC 系统，该系统由 User 节点、Helper 节点和 AP 节点组成。在这里，Helper 节点可以是物联网传感器、智能手机或笔记本电脑，它们就在附近，并具有一定的计算和通信资源。贡献：

• 首先，对于部分卸载，用户任务被划分为三个部分：本地计算、卸载到 Helper 和卸载到 AP。为了最小化 User 和 Helper 在用户计算延迟限制下的总能耗，我们联合优化了 User 的任务分配、User 和 Helper 的 CPU 频率、卸载的时间和传输功率分配。一般来说，非凸问题可以重新表述为凸问题。利用拉格朗日对偶方法，得到半封闭形式的全局最优解。
• 接下来，对于二元卸载，应该通过在三种计算模式中选择一种，即 User 本地计算、Helper 本地计算和 AP 计算。为了解决由此产生的能耗最小化问题，开发了一种有效的优化算法。首先选择计算模式，然后优化相应的联合假设和通信资源分配。
• 最后，大量的数值结果表明，与没有这种联合设计的其他基准方案相比，所提出的联合计算和通信协作方法在计算能力和系统能效方面都取得了显著的性能提高。

System Model

参数	含义
\(T\)	自定义的时间块长度 \(\ge \tau_1 + \tau_2 + \tau_3 + \tau_4\)，输出相比于输入足够小，忽略结果输出的时间
\(\tau_i\)	第 \(i\) 个时隙的长度
\(L\)	整个时间块内的任务长度（比特数）= \(l_u + l_h + l_a\)
\(l_u\)	User 节点执行的任务长度
\(l_h\)	Helper 节点执行的任务长度，\(= \tau_1 r_{01} (P_1)\)
\(l_a\)	AP 节点执行的任务长度
\(h_{01}\)	User 节点向 Helper 节点传输 \(l_u\) 的通信信道增益
\(P_1 h_{01}\)	接收功率 = 传输功率 * 信道增益
\(r_{01} (P_1)\)	数据传输速率函数，表示第一时隙从 User 到 Helper 的数据传输速率。 根据香农公式，即最大信息传输速率 \(C = B \log_2(1+S/N)\)，得 \(r_{01} (P_1) = B \log_2 (1 + \frac{P_1 h_{01}}{\Gamma \sigma_1^2})\)
\(r_0(P_2)\)	同上，表示第二时隙从 User 到 Helper 的数据传输速率，\(r_0 (P_2) = B \log_2 (1 + \frac{P_2 h_0}{\sigma_0^2})\)
\(r_1(P_3)\)	同上，表示第三时隙从 Helper 到 AP 的数据传输速率，\(r_1 (P_3) = B \log_2 (1 + \frac{P_3 h_1}{\sigma_0^2})\)
\(\Gamma\)	由实际调制编码带来的信道容量变化系数，是一个常数，本文假设为 1
\(\sigma_0\)	AP 接收的噪声功率
\(\sigma_1^2\)	Helper 的加性高斯白噪声功率
\(P_{u,\max}\)	用户的最大发射功率，因此 \(0 \le P_1 \le P_{u,\max}\)
\(\mathbf{P}\)	\([P_1, P_2, P_3]\)，每个时隙的传输功率：\(User \overset{l_h}{\rightarrow} Helper, User \overset{l_a}{\rightarrow} Helper, Helper \overset{l_a}{\rightarrow} AP\)
\(\mathbf{\mathcal{l}}\)	\([l_1,l_2,l_3]\)，每个时隙的任务长度：Helper 计算、Helper 中继接收 User、Helper 中继传给 AP
\(\bf{\tau}\)	\([\tau_1,\tau_2,\tau_3]\)，每个时隙的长度：前三个需要通信的时隙
\(E_1^{offl}\)	User 节点卸载到 Helper 节点的能耗，\(= \tau_1 P_1\)
\(E_u^{comp}\)	\(\frac{\kappa_u c_u^3 l_u^3}{T^2}\)
\(E_h^{comp}\)	\(\frac{\kappa_h c_h^3 l_h^3}{(T - \tau_1)^2}\)

Problem Formulation

P1. Partial Offloading

\[\begin{align} \min\limits_{\mathbf{P, \tau, \mathcal{l}}} & \quad (\sum_{i=1}^3 E_i^{offl}) + E_u^{comp} + E_h^{comp} = \sum_{i=1}^3 \tau_i P_i + \frac{\kappa_u c_u^3 l_u^3}{T^2} + \frac{\kappa_h c_h^3 l_h^3}{(T - \tau_1)^2} \\ subject \ to & \quad l_h \le \tau_1 r_{01} (P_1) \\ & \quad l_a \le \min(\tau_2 r_0 (P_2) + \tau_3 r_1 (P_3), \tau_2 r_{01} (P_2)) \\ & \quad 0 \le P_j \le P_{u,\max}, \forall j \in \{1, 2\} \\ & \quad 0 \le P_3 \le P_{h,\max} \\ & \quad 0 \le \tau_i \le T, \forall i \in \{1, 2, 3\} \\ & \quad l_u \ge 0, l_h \ge 0, l_a \ge 0 \\ & \quad l_u + l_h + l_a = L \\ & \quad c_u l_u \le T f_{u, \max} \\ & \quad c_h l_h \le (T - \tau_1) f_{h, \max} \\ & \quad \tau_1 + \tau_2 + \tau_3 + \frac{c_a l_a}{f_{a,\max}} \le T \end{align} \]

这是一个非凸问题，因为优化变量 \(\mathbf{\tau}\) 和 \(\mathbf{P}\) 耦合在优化问题及前两个约束中，对 \(f = \sum_{i=1}^3 \tau_i P_i\) 进行二阶条件判断，其 \(Hessian\) 矩阵半负定，显然为凹函数：

\[\nabla^2 f = \begin{bmatrix} 0 & 3 \\ 3 & 0\end{bmatrix} \]

P2. Binary Offloading

\[\begin{align} \min\limits_{\mathbf{P, \tau, \mathcal{l}}} & \quad \sum_{i=1}^3 \tau_i P_i + \frac{\kappa_u c_u^3 l_u^3}{T^2} + \frac{\kappa_h c_h^3 l_h^3}{(T - \tau_1)^2} \\ subject \ to & \quad l_u \in \{0,L\}, l_h \in \{0,L\}, l_a \in \{0,L\} \\ & \quad l_u + l_h + l_a = L \\ & \quad c_u l_u \le T f_{u, \max} \\ & \quad c_h l_h \le (T - \tau_1) f_{h, \max} \\ & \quad \tau_1 + \tau_2 + \tau_3 + \frac{c_a l_a}{f_{a,\max}} \le T \\ & \quad l_h \le \tau_1 r_{01} P_1 \\ & \quad l_a \le \min(\tau_2 r_0 P_2 + \tau_3 r_1 P_3, \tau_2 r_{01} P_2) \\ & \quad 0 \le P_j \le P_{u,\max}, \forall j \in \{1, 2\} \\ & \quad 0 \le P_3 \le P_{h,\max} \\ & \quad 0 \le \tau_i \le T, \forall i \in \{1, 2, 3\} \\ \end{align} \]

是一个混合整数非线性规划问题，因为其中的优化变量 \(\mathcal{l} = l_u, l_h, l_a\) 都是整型变量。其中必有两个分量为 0，剩下一个为整数 \(L\)。

Optimal Solution

引入辅助变量

通过引入辅助变量，令 \(\mathbf{E} = \{E_1, E_2, E_3\} = \{\tau_1 P_1, \tau_2 P_2, \tau_3 P_3\}\)，将耦合的两个优化变量合为一个，可以将问题 P1 转化为凸优化问题：

\[\begin{align} \min\limits_{\mathbf{E, \tau, l}} & \quad \sum_{i=1}^3 E_i + \frac{\kappa_u c_u^3 l_u^3}{T^2} + \frac{\kappa_h c_h^3 l_h^3}{(T - \tau_1)^2} \\ subject \ to & \quad l_h \le \tau_1 r_{01} (\frac{E_1}{\tau_1}) \\ & \quad l_a \le \tau_2 r_0 (\frac{E_2}{\tau_2}) + \tau_3 r_1 (\frac{E_3}{\tau_3}) \\ & \quad l_a \le \tau_2 r_{01} (\frac{E_2}{\tau_2}) \\ & \quad 0 \le E_j \le \tau_j P_{u,\max}, \forall j \in \{1, 2\} \\ & \quad 0 \le E_3 \le \tau_3 P_{h,\max} \\ & \quad l_u + l_h + l_a = L \\ & \quad c_u l_u \le T f_{u, \max} \\ & \quad c_h l_h \le (T - \tau_1) f_{h, \max} \\ & \quad \tau_1 + \tau_2 + \tau_3 + \frac{c_a l_a}{f_{a,\max}} \le T \\ & \quad 0 \le \tau_i \le T, \forall i \in \{1, 2, 3\} \\ & \quad l_u \ge 0, l_h \ge 0, l_a \ge 0 \\ \end{align} \]

至于约束函数的凹凸性，原文解释的比较简单，我的理解如下：

\[\begin{align*} & 以 \ l_h - \tau_1 r_{01} \big{(} \frac{E_1}{\tau_1} \big{)} \le 0 \ 为例 \\ & 由于 \ l_h \ 是单变量线性函数 \\ & 只需考虑 \ \tau_1 r_{01} \big{(} \frac{E_1}{\tau_1} \big{)} \\ & 对其进行等价变换，令 \ \tau_1 r_{01} \big{(} \frac{E_1}{\tau_1} \big{)} \underset{r_{01} = f}{\overset{\tau_1 = x, E_1 = xt}{\Longrightarrow}} g(x,t) = xf(t) \\ & 则有 \ \nabla^2g = \begin{bmatrix} 0 & f^{'}(t) \\ f^{'}(t) & x f^{''}(t)\end{bmatrix} \le 0 \\ & 则 \ g \ 为凹函数 \\ & 则 \ -g \ 为凸函数 \end{align*} \]