1-1. 凸优化（笔记）

Course：电子科技大学 - 最优化理论
Textbook：《凸优化》- Stephen Boyd
ISBN：9787302297567

一、引言

1.1. 数学优化

1.1.1. 优化问题

数学优化问题指可以写成如下形式的问题：

\[\begin{equation} \begin{aligned} minimize \quad & f_0(x) \\ subject \ to \quad & f_i(x) \le b_i, i = 1, ..., m \end{aligned} \end{equation} \]

其中，各个变量及符号的含义如下：

• \(x \in \bf{R^n}\)：优化变量
• \(f_0(x): \bf{R^n} \rightarrow \bf{R}\)：目标函数
• \(f_i(x): \bf{R^n} \rightarrow \bf{R}\)：约束函数
• \(b_i\)：约束上限或者约束边界
• \(x^*\)：称为最优解或者解，即对于任意满足所有约束函数的优化变量取值中，使得目标函数值最小的那个优化变量取值

1.1.2. 线性规划问题

一般只考虑具有特殊形式的优化问题，如目标函数和约束函数都为线性函数，此类问题称为线性规划。其目标函数和约束函数满足如下性质：

\[f_i(\alpha x + \beta y) = \alpha f_i(x) + \beta f_i(y), \quad i = 0, 1, ..., m \]

1.1.3. 凸优化问题

凸优化问题也是一种具有特殊形式的优化问题，是本课程讨论的主要对象，且线性规划也属于一种特殊的凸优化问题。凸优化问题的目标函数和约束函数满足如下性质：

\[f_i(\alpha x + \beta y) \le \alpha f_i(x) + \beta f_i(y), \quad i = 0, 1, ..., m \]

1.2. 优化问题求解

1.2.1. 最小二乘问题

最小二乘问题是一个典型的无约束函数的凸优化问题（\(m = 0\)），其具体形式如下：

\[\begin{equation} \begin{aligned} minimize \quad & f_0(x) = \Vert A x - b \Vert_2^2 = \sum_{i=1}^{k} (a_i^T x - b_i)^2 \end{aligned} \end{equation} \]

其中 \(A \in \bf{R^{k \times n}} (k \ge n)\)，\(a_i^T\) 是 \(A\) 的行向量，\(x \in \bf{R^n}\) 是优化变量。
最小二乘问题常用于回归分析，最优控制，参数估计以及数据拟合等。求解最小二乘问题一般是一项成熟的技术，其有通用方法，即将其转换为一组线性方程并求出 \(x\) 的解析式：

\[\begin{equation} \begin{aligned} & (A^T A) x = A^T b \\ & x = (A^T A)^{-1} A^T b \end{aligned} \end{equation} \]

判断一个问题是否是最小二乘问题
验证其目标函数是否是二次函数，并检验该二次函数是否半正定。此外加权系数以及正则化参数都是最小二乘问题的扩展，这些参数可以使最小二乘问题更加贴合实际应用。

1.2.2. 线性规划问题

相比于最小二乘，虽然线性规划问题的解没有一个简单的解析式，但也存在很多有效的求解方法，如 Dantzig 单纯形法，内点法。使用小型台式机可在几秒的时间内处理数百变量，数千约束条件的线性规划问题。求解程序已经嵌入到了很多工具箱或者程序包中。

1.2.3. 凸优化问题

凸优化问题的解也没有一个简单的解析式，但是内点法求解在实际应用中就很有效。一些情况下，内点法可以在多项式时间内以给定精度求解这些凸优化问题。

从概念上看，使用凸优化和使用最小二乘及线性规划类似。将某个应用问题表述为凸优化问题，即可快速有效的进行求解。但凸优化问题的识别比较困难，且转换为凸优化问题的过程中存在更多技巧。如果能将一个问题表述为凸优化问题，那么求解它几乎只是一项有套路的技术了。

1.2.4. 非线性优化

非线性优化，其目标函数或约束函数为非线性函数，当然也不一定是凸函数。对于一般的非线性规划问题，还没有比较好的求解方案。一般对于此类问题，都是放宽某些限制，采取不同的途径进行求解。

1. 局部优化：放宽对解的最优性的要求，不再寻找全局最优解，改为寻找局部最优解。这种方法需要估计优化变量的初值，其对优化结果往往影响很大，且这是一项比较困难且没有保障性的工作，需要更多的技巧
2. 全局优化：付出效率的代价寻找全局最优解，一般问题规模较小且求解时间比较长
3. 非凸问题中的凸优化应用：局部优化结合凸优化技术、非凸优化中的凸启发式算法、全局优化的界

1.3. 符号

1. \(R, R_+, R_{++}\)：实数集，非负实数集，正实数集
2. \(C\)：复数集
3. \(R^{n}\)：n 维实向量
4. \(R^{m \times n}\)：\(m \times n\) 实矩阵
5. \(S^n, S^n_{+}, S^n_{++}\)：对称 \(n \times n\) 矩阵，对称半正定 \(n \times n\) 矩阵，对称正定 \(n \times n\) 矩阵
6. \(I\)：单位阵
7. \(\lambda_i\)：第 \(i\) 大特征值
8. \(\sigma_i\)：第 \(i\) 大奇异值

1.4 章节分类

• 1 ~ 5：理论
• 6 ~ 8：应用
• 9 ~ 11：算法

二、凸集

2.1. 仿射集合，凸集和锥

2.1.1. 仿射集

仿射集
对于集合 \(C \in \bf{R^n}\)，连接其中任意两个不同点所成的直线，仍在该集合中，那么称集合 \(C\) 是仿射的。数学公式表述为：

\[\begin{align} & \forall x_1, x_2 \in C, \ \theta \in \mathbf{R} \ \Rightarrow \ \theta x_1 + (1 - \theta) x_2 \in C \\ & \forall x_1, ..., x_k \in C, \ \theta_1, ..., \theta_k \in \mathbf{R}, \ \theta_1 + ... + \theta_k = 1 \ \Rightarrow \ \theta_1 x_1 + ... + \theta_k x_k \in C \end{align} \]

其中，满足条件的 \(\theta_i\) 和 \(x_i\) 的线性组合：\(\theta_1 x_1 + ... + \theta_k x_k\) 称为集合 \(C\) 的仿射组合

仿射包
称由集合 $ C \in \mathbf{R^n} $ 的所有仿射组合，组成的集合称为仿射包，记为 $ \mathbf{aff} \ C$：

\[\begin{align} & \mathbf{aff} \ C = \{ \theta_1 x_1 + ... + \theta_k x_k \ | \ x_1, ..., x_k \in C, \ \theta_1, ..., \theta_k \in \mathbf{R}, \ \theta_1 + ... + \theta_k = 1 \} \end{align} \]

2.1.2. 凸集

凸集
对于集合 \(C \in \bf{R^n}\)，连接其中任意两个不同点所成的线段，仍在该集合中，那么称集合 \(C\) 是凸的。数学公式表述为：

\[\begin{align} & \forall x_1, x_2 \in C, \theta \in \mathbf{R} , 0 \le \theta \le 1 \ \Rightarrow \ \theta x_1 + (1 - \theta) x_2 \in C \\ & \forall x_1, ..., x_k \in C, \ \theta_1, ..., \theta_k \in \mathbf{R} , \ 0 \le \theta_i \le 1, \ \theta_1 + ... + \theta_k = 1 \ \Rightarrow \ \theta_1 x_1 + ... + \theta_k x_k \in C \end{align} \]

其中，满足条件的 \(\theta_i\) 和 \(x_i\) 的线性组合：\(\theta_1 x_1 + ... + \theta_k x_k\) 称为集合 \(C\) 的凸组合

凸包
称由集合 $ C \in \mathbf{R^n} $ 的所有凸组合，组成的集合称为凸包，记为 $ \mathbf{conv} \ C$：

\[\begin{align} & \mathbf{conv} \ C = \{ \theta_1 x_1 + ... + \theta_k x_k \ | \ x_1, ..., x_k \in C, \ \theta_1, ..., \theta_k \in \mathbf{R}, \ 0 \le \theta_i \le 1\} \end{align} \]

2.1.3. 锥

锥

对于集合 \(C \in \bf{R^n}\)，从其顶点到其中任意点的射线，仍在该集合中，那么称集合 \(C\) 是一个锥。数学公式表述为：

\[\begin{align} & \forall x \in C, \ \theta \in \mathbf{R}, \ \theta \ge 0 \ \Rightarrow \ \theta x \in C \end{align} \]

凸锥
如果集合 \(C \in \bf{R^n}\) 是锥且是凸集，则称其为凸锥，如下图。数学公式表述为：

\[\begin{align} & \forall x_1, ..., x_k \in C, \ \theta_1, ..., \theta_k \in \mathbf{R_+} \ \Rightarrow \ \theta_1 x_1 + ... + \theta_k x_k \in C \end{align} \]

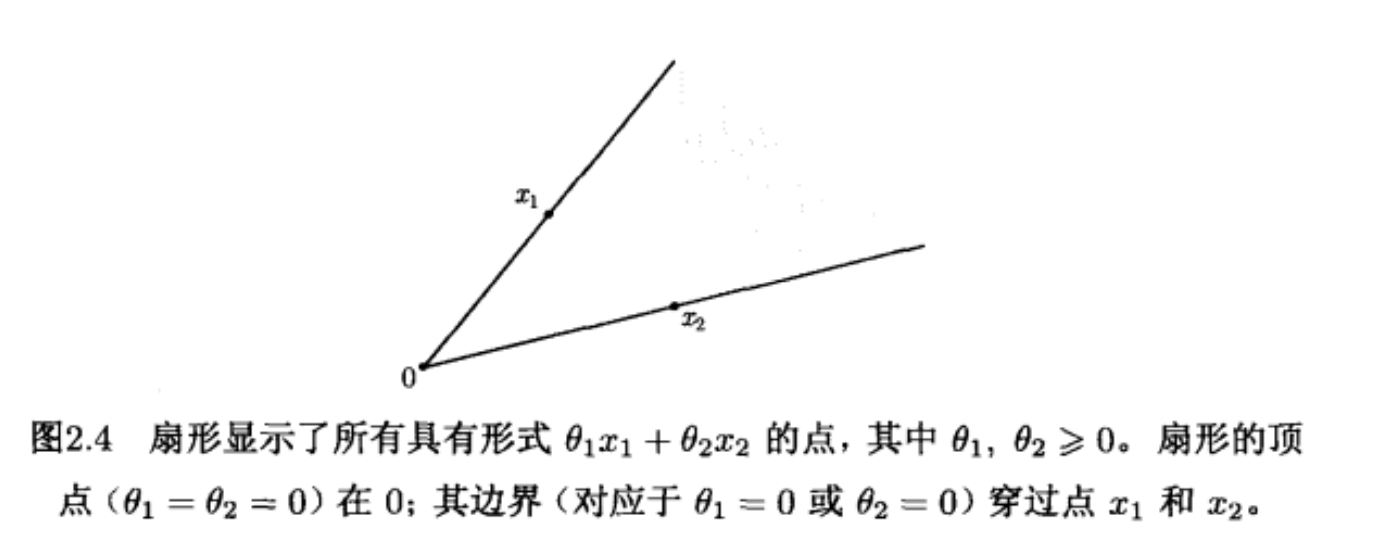
锥组合
其中，满足条件的 \(\theta_i\) 和 \(x_i\) 的线性组合：\(\theta_1 x_1 + ... + \theta_k x_k\) 称为集合 \(C\) 的锥组合

锥包
称由集合 \(C \in \bf{R^n}\) 的所有锥组合，组成的集合称为锥包。数学公式表述为：

\[\begin{align} & \{ \theta_1 x_1 + ... + \theta_k x_k \ | \ x_i \in C, \theta_i\in \mathbf{R_+}, i = 1, ..., k \} \end{align} \]

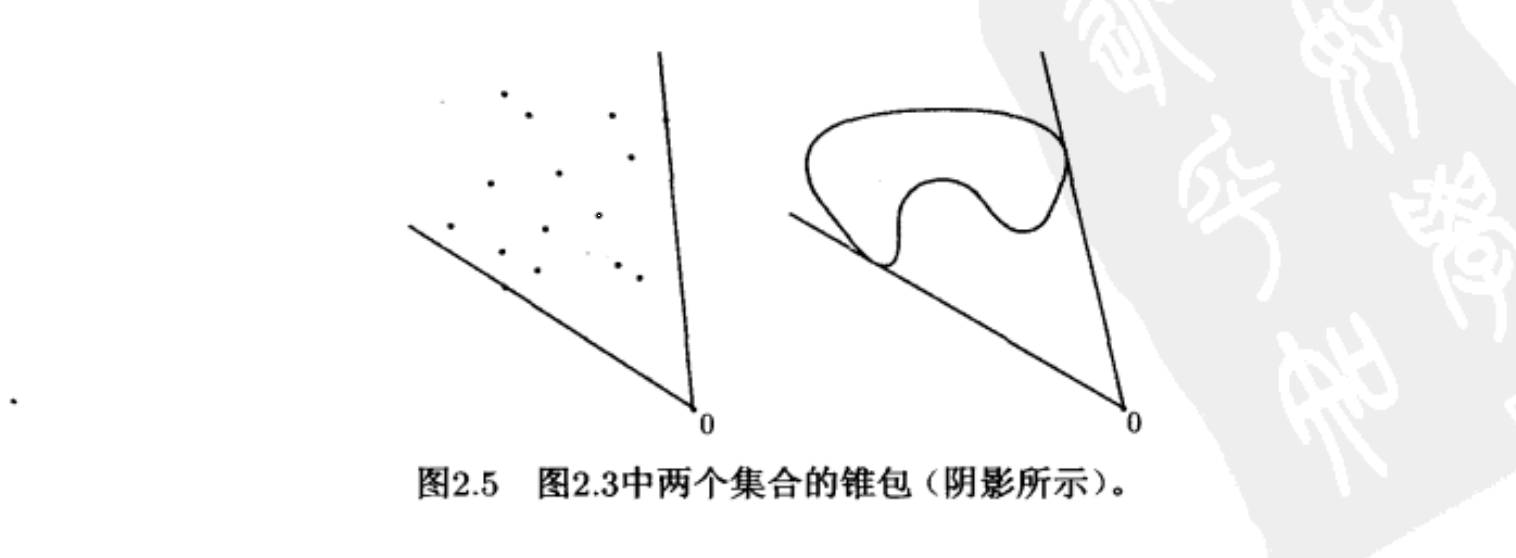
2.2. 重要的例子

2.2.1. 简单的例子

1. \(\emptyset, {x_1}, R^n\)：空集、单点集、全空间都是仿射且凸的
2. 任意直线都是仿射的
3. 任意通过零点的直线都是子空间，也是凸锥
4. 任意一条线段是凸的，但不是仿射的
5. 任意子空间都是仿射的，凸的且凸锥

2.2.2. 超平面

形如 $ \{ x \ | \ a^T x = b, a \in \mathbf{R^n} , a \neq 0, b \in \mathbf{R^n} \}$ 组成的点集称为超平面。在二维空间中可以想象为一条直线，三维空间为一个平面。

2.2.3. 半空间

一个超平面将全空间分为两个半空间，分别表示为：

\[\begin{equation} \begin{aligned} & \{x \ | \ a^T x \le b, a \in \mathbf{R^n} , a \neq 0, b \in \mathbf{R} \} \\ & \{x \ | \ a^T x \ge b, a \in \mathbf{R^n} , a \neq 0, b \in \mathbf{R} \} \end{aligned} \end{equation} \]

半空间的边界 \(\{x \ | \ a^T x = b \}\) 为超平面，内部如 \(\{x \ | \ a^T x < b \}\) 称为开半空间。

2.2.4. Euclid 球和椭球

\(\mathbf{R^n}\) 中的 Euclid 球（简称为球），具有以下形式：

\[B(x_c, r) = \{ x \ | \ \Vert x - x_c \Vert_2 \le r \} = \{ x \ | \ (x - x_c)^T (x - x_c) \le r^2 \} \]

其中标量 \(r > 0\) 表示球的半径，\(\Vert · \Vert_2\) 为 Euclid 范数（欧几里得范数），向量 \(x_c\) 表示球心，\(B(x_c, r)\) 表示距离球心不超过 \(r\) 的所有点组成的集合。显然，球是凸集。

\(\mathbf{R^n}\) 中的椭球，具有以下形式：

\[\mathscr{E} = \{ x \ | \ (x - x_c)^T P^{-1} (x - x_c) \le 1 \} \]

其中 \(P = P^T \succ 0\)，即 \(P\) 为对称正定矩阵。向量 \(x_c\) 表示椭球的球心，矩阵 \(P\) 决定了椭球从球心向各个方向扩展的幅度。椭球的半轴长度由矩阵 \(P\) 的特征值 \(\sqrt{\lambda_i}\) 决定。球可以看做 \(P = r^2 I\) 的椭球。同样的，椭球也是凸集。

2.2.5. 范数球和范数锥

2.2.6. 多面体

多面体是有限个半空间和超平面的交集，具有以下形式：

\[\mathscr{P} = \{ x \ | \ a_i^T x \le b_i, \ i = 1, ..., m, \ c_j^T x = d_j, j = 1, ..., n \} \]

仿射集合（子空间、超平面、直线），射线，线段和半空间都是多面体。显然，多面体也是凸集。有界的多面体也称为多胞形。

2.3. 保凸运算

2.3.1. 交集

交集运算是保凸的，如果 \(S_1, S_2\) 均为凸集，则 \(S_1 \cap S_2\) 也是凸集。这个性质可以扩展到无穷个集合的交。比如多面体是半空间和超平面的交集，因此它是凸的。

2.3.2. 仿射函数

对于仿射函数 \(f: \mathbf{R^m} \rightarrow \mathbf{R^n}\)，如果其具有如下形式：\(f(x) = A x + b, \ A \in \mathbf{R^{m \times n}}, \ b \in \mathbf{R^m}\)，那么该函数是保凸的。即如果原象 \(S \in \mathbf{R^n}\) 是凸的，那么 \(S\) 在 \(f\) 下的象 \(f(S) = \{ f(x) \ | \ x \in S \}\)也是凸的。下面是仿射函数的一些简单应用：

伸缩
如果 \(S \in \mathbf{R^n}\) 是凸集，\(\alpha \in \mathbf{R}\)，那么集合 \(\alpha S = \{ \alpha x \ | \ x \in S \}\) 是凸的。

平移
如果 \(S \in \mathbf{R^n}\) 是凸集，\(a \in \mathbf{R^n}\)，那么集合 \(a + S = \{ a + x \ | \ x \in S \}\) 是凸的。

集合的和
如果 \(S_1, S_2\) 是凸集，那么集合 \(S_1 + S_2 = \{ x_1 + x_2 \ | \ x_1 \in S_1, \ x_2 \in S_2 \}\) 是凸集。

集合的直积/Cartesian 乘积
如果 \(S_1, S_2\) 是凸集，那么集合 \(S_1 \times S_2 = \{ (x_1, x_2) \ | \ x_1 \in S_1, \ x_2 \in S_2 \}\) 是凸集。

集合的部分和
如果 \(S_1, S_2\) 是凸集，那么集合 \(S = \{ (x, y_1 + y_2) \ | \ (x, y_1) \in S_1, \ (x, y_2) \in S_2 \}\) 是凸集。

2.3.3. 透视函数

定义 \(P: \mathbf{R^{n+1}} \rightarrow \mathbf{R^{n}}\)，\(P(\mathbf{Z}, t) = \mathbf{Z} / t\)，其定义域为 \(\mathbf{dom} P = \mathbf{R^{n}} \times \mathbf{R_{++}}\)，即 \(Z \in \mathbf{R^{n}}, t \in \mathbf{R_{++}}\)。透视函数将向量规范化，使得最后一维化为 1 并舍弃之。

对于任意的集合 \(C \in \mathbf{dom} P\) 为凸集，则 \(P(C)\) 是凸的。逆命题同样成立。

2.3.4. 线性分式函数

线性分式函数是由透视函数和仿射函数复合而成的函数。即若 \(g(x)\) 为仿射函数，则 \(P(g(x))\) 称为线性分式函数。形如：

\[g(x) = \begin{bmatrix} A \\ c^T \end{bmatrix} x + \begin{bmatrix} b \\ d \end{bmatrix}, A \in \mathbf{R^{m \times n}}, b \in \mathbf{R^{m}}, c \in \mathbf{R^{n}}, d \in \mathbf{R} \]

\[P(g(x)) = \frac{(Ax+b)}{(c^T x+d)}, \mathbf{dom} P = \{ x \ | \ c^T x + d > 0\} \]

解释
我们可以将线性分式函数表示为一个矩阵左乘 \((x, 1)\)，即：

\[Q \cdot \begin{pmatrix} x \\ 1 \end{pmatrix} = \begin{bmatrix} A & b \\ c^T & d \end{bmatrix} \cdot \begin{pmatrix} x \\ 1 \end{pmatrix} = \begin{pmatrix} Ax+b \\ c^T x + d \end{pmatrix} \]

然后将所得结果做归一化处理，使得最后一个分量变为 1，即 \(\begin{pmatrix} \frac{(Ax+b)}{(c^T x+d)} \\ 1 \end{pmatrix}\)。

三、凸函数

3.1. 定义与性质

3.1.1. 定义

定义一

如果 \(\mathbf{dom} f\) 是凸集，且对于 \(\forall x, y \in \mathbf{dom} f, 0 \le \theta \le 1\)，均有 $ f(\theta x + (1 - \theta) y) \le \theta f(x) + (1 - \theta) f(y) $ 成立，则称函数 \(f: \mathbf{R^n} \rightarrow \mathbf{R}\) 是凸的。

从几何意义上看，这个不等式意味着 \((x, f(x)), (y, f(y))\) 之间的弦，在函数 \(f\) 图像的上方：

1. \(f\) 严格凸：当 \(x \ne y, 0 < \theta < 1\) 时，不等式严格成立
2. \(f\) 凹：函数 \(-f\) 是凸的
3. \(f\) 严格凹：函数 \(-f\) 是严格凸的

对于仿射函数，该不等式总是成立，因此所有的仿射函数都是既凸又凹的。即：一个函数既凸又凹 \(\Leftrightarrow\) 该函数为仿射函数。

定义二

一个函数是凸的，当且仅当其在与其定义域相交的任何直线上都是凸的。换言之，函数 \(f\) 是凸的，当且仅当对于任意的 \(x \in \mathbf{dom} f\) 和任意的向量 \(v\)，均有函数 \(g(t) = f(x + tv)\) 是凸的，其中 \(\mathbf{dom} g = \{ t \ | \ x + tv \in \mathbf{dom} f\}\)。

比如在 xoy 平面中的圆（包含其内部）为一个凸集，使用任意直线对其进行切割，得到的交集（空集、单点集、连接直线与圆两交点的线段）必定为凸集。再比如：

考虑在三维欧式空间中的抛物面： $$A：z = 𝑥^2+𝑦^2$$

任选一点 $x = (0,0)$ 和向量 $v = (1,1)$，以及标量 $t$，那么 $x + vt$ 可以表示二维空间中，通过 $(0,0)$ 和 $(1,1)$ 的直线，即 $x = y$（注意此直线在三维空间中，表示一个空间平面）。 则 $x+vt = (0,0)^T + (t,t)^T = (t,t)^T$，$z = t^2 + t^2 = 2t^2$。即交线方程为 $z = 2t^2$，是一个开口向上的抛物线，显然是凸的。

如果对于任取的 $x, v$，得到的交线都是凸的，那么原函数 $A$ 是凸的。这里的任取，使得 $A$ 的所有 $n-1$ 维切割方式（无数种）都被遍历到。

定义三（一阶条件）

假设 \(f\) 可微（即其梯度 \(\nabla f = (\frac{\partial f}{\partial x_1}, ..., \frac{\partial f}{\partial x_n})\) 在开集 \(\mathbf{dom} f\) 内处处存在），则函数 \(f(x)\) 是凸函数 \(\Leftrightarrow\) \(\mathbf{dom} f\) 是凸集，且 \(\forall x, y \in \mathbf{dom} f\) 均有如下不等式成立：

\[f(y) - f(x) \ge \nabla f(x)^T (y-x) \]

下图描述了该不等式的几何意义（函数图像在切线上方）：

定义四（二阶条件）

假设 \(f\) 二阶可微（即对于开集 \(\mathbf{dom} f\) 内任意一点，其 \(Hessian\) 矩阵或者二阶导数 \(\nabla^2 f\) 存在）。则函数 \(f(x)\) 是凸函数 \(\Leftrightarrow\) \(\mathbf{dom} f\) 是凸集，且 \(\nabla^2 f(x) \succeq 0\)。 其中：

\[\nabla^2 f(x) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 x_2} & ... & \frac{\partial^2 f}{\partial x_1 x_n} \\ \frac{\partial^2 f}{\partial x_2 x_1} & \frac{\partial^2 f}{\partial x_2^2} & ... & \frac{\partial^2 f}{\partial x_2 x_n} \\ ... & ... & ... & ... \\ \frac{\partial^2 f}{\partial x_n x_1} & \frac{\partial^2 f}{\partial x_n x_2} & ... & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} \]

3.1.2. 约定及性质

扩展值延伸（定义域延伸）
通常可以将凸函数定义域外的取值定义为 \(\infty\)，来将凸函数的定义延伸至全空间 \(\mathbf{R^n}\)，得到的新函数我们记为：

\[\tilde{f} = \begin{split} \left\{ \begin{array} \ f(x) & x \in \mathbf{dom} f \\ \infty & x \notin \mathbf{dom} f \end{array} \right. \end{split} \]

凸集的示性函数
凸集 \(C\) 的示性函数 \(\tilde{I}_C(x)\) 仍是一个凸集，其被定义为：

\[\tilde{I}_C(x) = \begin{split} \left\{ \begin{array} \ 0 & x \in C \\ \infty & x \notin C \end{array} \right. \end{split} \]

定义域限制
在判断函数的凹性和凸性时，不管是一阶条件还是二阶条件，\(\mathbf{dom} f\) 是凸集这个前提条件必须满足。

3.2. 重要的例子

3.2.1. 简单的例子

下面的示例是定义在 \(\mathbf{R}\) 上的一些函数，其自变量为标量 \(x\)：

1. 指数函数：\(\forall a \in \mathbf{R}\)，函数 \(e^{ax}\) 在 \(\mathbf{R}\) 上是凸的
2. 幂函数：当 $a \ge 1 $ 或 \(a \le 0\) 时，函数 \(x^a\) 在 \(\mathbf{R_{++}}\) 上是凸的；当 \(0 \le a \le 1\) 时，函数 \(x^a\) 在 \(\mathbf{R_{++}}\) 上是凹的
3. 绝对值幂函数：当 \(p \ge 1\) 时，函数 \(|x|^p\) 在 \(\mathbf{R}\) 时凸的
4. 对数函数：函数 \(\log x\) 在 \(\mathbf{R_{++}}\) 上是凹的
5. 负熵：函数 \(x \log x\) 在定义域（可定义 \(f(0) = 0\)）上是凸的

下面的示例是定义在 \(\mathbf{R^n}\) 上的一些函数，其自变量为 \(x \in \mathbf{R^n}\)：

1. 范数：\(\mathbf{R^n}\) 上的任意范数均为凸函数
2. 最大值函数：函数 \(f(x) = \max \{ x_1, ..., x_n\}\) 在 \(\mathbf{R^n}\) 上是凸的
3. 二次-线性分式函数：函数 \(f(x,y) = \frac{x^2}{y}\) 是凸函数，其定义域为 \(\mathbf{dom} f = \mathbf{R} \times \mathbf{R_{++}}\)
4. 指数和的对数：函数 \(f(x) = \log (e^{x_1} + ... + e^{x_n})\) 在 \(\mathbf{R^n}\) 上是凸的，这个函数可以看成最大值函数的解析近似
5. 几何平均：函数 \(f(x) = (x_1 \cdot x_2 \cdot ... \cdot x_n)^{1/n}\) 在定义域 \(\mathbf{dom} f \in \mathbf{R^n_{++}}\) 上是凹函数
6. 对数-行列式：函数 \(f(X) = \log \det X\) 在定义域 \(\mathbf{dom} f \in \mathbf{S^n_{++}}\) 上是凹函数

3.2.2. 下水平集

函数 \(f: \mathbf{R^n} \rightarrow \mathbf{R}\) 的 \(\alpha\) 下水平集，被定义为 \(C_\alpha = \{ x \in \mathbf{dom} f \ | \ f(x) \le \alpha \}\)。注意，下水平集是定义域的子集，不要理解为函数图像的一部分。

凸函数的任意 \(\alpha\) 下水平集都是凸集，反之则不一定。例如 \(f(x) = -e^x\) 不是凸函数，但其所有下水平集都是凸集。当然，如果 \(f\) 是凹函数，那么它的 \(\alpha\) 上水平集 \(\{ x \in \mathbf{dom} f \ | \ f(x) \ge \alpha \}\) 也是凸集。那么我们有如下结论：如果一个集合是某个凸函数的下水平集或者凹函数的上水平集，那么该集合一定是凸集。

通俗的讲，以 \(f: y = x^2\) 为例，划一条线 \(y = \alpha\)，则使得 \(y \le \alpha\) 的所有 \(x\) 组成的集合，就是 \(f\) 的 \(\alpha\) 下水平集。

3.2.3. 上境图

函数 \(f: \mathbf{R^n} \rightarrow \mathbf{R}\) 的上境图，被定义为 \(\mathbf{epi} f = \{ (x, t) \ | \ x \in \mathbf{dom} f, f(x) \le t \}\)。可以将其理解为由 \(f(x)\) 图像上方的点所组成的集合。它是 \(\mathbf{R^{n+1}}\) 空间的一个子集（这里不用疑惑，函数维度和空间维度本就不一致，比如二维空间的函数图像其自变量为一维）。

一个函数是凸函数，当且仅当其上境图是凸集。一个函数是凹函数，当且仅当其亚图 \(\mathbf{hypo } f = \{ (x, t) \ | \ x \in \mathbf{dom} f, f(x) \ge t \}\) 是凸集。

通俗的讲，以 \(f: y = x^2\) 为例，则图像上方的全部区域，就是 \(f\) 的上境图。对应概念亚图，就是图像下方的全部区域。当然二者都是包含边界的。

3.3. 保凸运算

3.3.1. 非负加权和

如果函数 \(f\) 是凸函数，且标量 \(\alpha \ge 0\)，则 \(\alpha f\) 也是凸函数。如果函数 \(f_1, f_2\) 均是凸函数，则 \(f_1 + f_2\) 也是凸函数。将凸函数的非负伸缩和求和运算结合起来，得到的函数仍然是凸函数。类似的结论有：

1. 凸函数的非负加权求和仍为凸函数
2. 凹函数的非负加权求和仍为凹函数
3. 严格凸（凹）函数的非负、非零加权求和仍为严格凸（凹）函数

3.3.2. 复合仿射映射

设函数 \(f: \mathbf{R}^n \rightarrow \mathbf{R}, A \in \mathbf{R}^{n \times m}, b \in \mathbf{R}^n\)，定义函数 \(g: \mathbf{R}^m \rightarrow \mathbf{R}\)：

\[g(x) = f(Ax + b) \]

其中 \(\mathbf{dom} g = \{x \ | \ Ax+b \in \mathbf{dom} f\}\)。若 \(f\) 为凸（凹）函数，则 \(g\) 同为凸（凹）函数。

3.3.3. 逐点最大函数（有限个函数的最大值函数）

若 \(f_1(x), ..., f_m(x)\) 为凸函数，则 \(f(x) = \max \{ f_1(x), ..., f_m(x) \}\) 也是凸函数，其中 \(\mathbf{dom} f = \bigcap_{i=1}^{m} \mathbf{dom} \ f_i(x)\)。

3.3.4. 逐点上确界和逐点下确界

当函数数量扩展到无限个时，可能不存在最大值或最小值，但可以用上界和下界来衡量。例如，如果对于任意 \(y \in \mathscr{A}\)，函数 \(f(x,y)\) 关于 \(x\) 都是凸的，则逐点上确界函数：

\[g(x) = \sup_{y \in \mathscr{A}} \ f(x, y) \]

关于 \(x\) 也是凸的。类似的，一系列凹函数的逐点下确界也是凹函数。

3.3.5. 向量的最大 \(r\) 个分量和

\(\forall x \in \mathbf{R}^n\)，从 \(n\) 个分量中取出 \(r\) 个，使这 \(r\) 个分量之和最大。令函数 \(f(x)\) 为这 \(r\) 个分量之和，即：

\[f(x) = \max(\sum_{i=1}^r x_i) \]

因为 \(f(x)\) 是 \(C_n^r\) 个线性函数的逐点最大，所以 \(f(x)\) 也是凸（既凸又凹）函数。

3.3.6. 复合函数

给定函数 \(h: \mathbf{R}^k \rightarrow \mathbf{R}, g: \mathbf{R}^n \rightarrow \mathbf{R}^k\)，定义复合函数 \(f: \mathbf{R}^n \rightarrow \mathbf{R}\)：

\[f(x) = h(g(x)) \]

其中，\(\mathbf{dom} f = \{ x \in \mathbf{dom} g \ | \ g(x) \in \mathbf{dom} h\}\)。有如下规定：

1. 考虑一般情况，\(n, k \ge 1\)，\(h, g\) 不一定可微，\(\mathbf{dom} \ g, \mathbf{dom} \ h\) 不一定是全空间；
2. 定义 \(\tilde{h}(x) = \begin{split} \left\{ \begin{array} \ h(x) & x \in \mathbf{dom} h \\ \infty & x \notin \mathbf{dom} h \ \& \ x \in \mathbf{R}^k（h 凸） \\ -\infty & x \notin \mathbf{dom} h \ \& \ x \in \mathbf{R}^k（h 凹） \end{array} \right. \end{split}\)

则关于复合函数 \(f(x) = h(g(x))\) 的凹凸性，有如下结论：

\(h\)	\(\tilde{h}\)	\(g\)	\(f\)
凸	不降	凸	凸
凸	不增	凹	凸
凹	不降	凹	凹
凹	不增	凸	凹

一些常见函数的复合结论：

1. 若 \(g\) 是凸函数，则 \(\exp(g(x))\) 是凸函数；
2. 若 \(g\) 是大于零的凹函数，则 \(\log g(x)\) 是凹函数；
3. 若 \(g\) 是大于零的凹函数，则 \(1/g(x)\) 是凹函数；
4. 若 \(g\) 是大于等于零的凸函数，\(p \ge 1\)，则 \(g^p(x)\) 是凸函数；

3.3.7. 透视函数

给定函数 \(f: \mathbf{R}^n \rightarrow \mathbf{R}\)，则 \(f\) 的透视 \(g: \mathbf{R}^{n+1} \rightarrow \mathbf{R}\) 定义为：

\[g(x,t) = t f(x/t) \]

其定义域为 \(\mathbf{dom} g = \{ (x,t) \ | \ x/t \in \mathbf{dom} f, t > 0\}\)。注意函数的透视与集合（凸集）的透视运算规则不同，但同样可以保持原函数（原集合）的凹凸性。

3.4. 共轭函数

设有函数 \(f: \mathbf{R}^n \rightarrow \mathbf{R}\)，则 \(f\) 的共轭函数 \(f^{*}: \mathbf{R}^n \rightarrow \mathbf{R}\) 定义为：

\[f^{*}(y) = \sup_{x \in \mathbf{dom} f}(y^T x - f(x)) \]

其中使逐点上确界有上限，即 \((y^T x - f(x))\) 在 \(\mathbf{dom} f\) 有上界的所有 \(y \in \mathbf{R}^n\) 构成了共轭函数的定义域。由于共轭函数是一系列关于 \(y\) 的仿射函数的逐点上确界，所以其为凸函数，无论 \(f\) 是否为凸函数。

3.5. 拟凸函数

定义
如果函数 \(f: \mathbf{R}^n \rightarrow \mathbf{R}\) 的定义域及任意 \(\alpha\) 下水平集均为凸集，则 \(f\) 称为拟凸函数：

\[S_\alpha = \{ x \in \mathbf{dom} f \ | \ f(x) \le \alpha \} \]

通俗的讲，以拟凸函数 \(y = \log x, x > 0\) 为例，在图像上任意划一条线 \(y = \alpha\)，则 \(y \le \alpha\) 对应的所有 \(x\) 取值的集合（就在 \(x\) 轴上），是一个凸集（而不是那种断断续续的）。

拟凹函数
如果函数 \(f: \mathbf{R}^n \rightarrow \mathbf{R}\) 的定义域及任意 \(\alpha\) 上水平集均为凸集，则 \(f\) 称为拟凹函数：

\[S_\alpha = \{ x \in \mathbf{dom} f \ | \ f(x) \ge \alpha \} \]

四、凸优化问题

4.1. 基本术语

4.1.1. 一般优化问题

优化问题的数学描述如下。其中，\(x \in \mathbf{R}^n\) 称为优化变量，\(f_0: \mathbf{R}^n \rightarrow \mathbf{R}\) 称为目标函数，\(f_i(x), h_i(x)\) 分别是不等式约束和等式约束。如果整个优化问题没有约束，则称为无约束优化问题

\[\begin{align*} minimize & \quad f_0(x) \\ subject \ to & \quad f_i(x) \le 0, i = 1, ..., m \\ & \quad h_i(x) = 0, i = 1, ..., p \end{align*} \]

对目标函数和所有约束函数均有定义的点集，称为优化问题的定义域。定义域中满足所有约束的点 \(x \in \mathscr{D}\)，称为可行解：

\[\mathscr{D} = \bigcap_{i=0}^m \mathbf{dom} f_i \cap \bigcap_{i=1}^p \mathbf{dom} h_i \]

最优值的定义如下（可以取无穷，即优化问题不可行），如果可行解 \(x^*\) 满足 \(f_0(x^*) = p^*\)，则该解被称为最优解：

\[p^* = \inf \{f_0(x) \ | \ f_i(x) \le 0, i=1,...,m, h_i(x) = 0, i=1,...,p \} \]

如果最优集是空集（没有最优解），但有 \(f_0(x) \le p^* + \epsilon, \epsilon > 0\) 成立，称这样的可行解 \(x\) 为\(\epsilon\) 次优解。

4.1.2. 凸优化问题

凸优化问题的数学描述如下，基本术语与一般优化问题保持一致：

\[\begin{align*} minimize & \quad f_0(x) \\ subject \ to & \quad f_i(x) \le 0, i = 1, ..., m \\ & \quad a_i^T x = b_i, i = 1, ..., p \end{align*} \]

相较于一般的优化问题，多了三个附加条件：

1. 目标函数和不等式约束函数必须是凸函数
2. 凸优化问题的定义域，可行集必定都是凸集
3. 等式约束必须是仿射的

4.2. 不等式与性质

4.2.1. 常用不等式

Jensen 不等式
也叫琴生不等式或均值不等式，最初的 Jensen 不等式如下：

\[f \big{(} \frac{x+y}{2} \big{)} \le \frac{f(x) + f(y)}{2} \]

可扩展为凸函数形式：

\[f(\theta x + (1 - \theta) y) \le \theta f(x) + (1 - \theta) f(y) \]

或无穷点集形式：

\[f \big{(} \frac{\sum_{i=1}^n x_i}{n} \big{)} \le \frac{\sum_{i=1}^n f(x_i)}{n} \]

算数几何平均不等式

\[\sqrt{ab} \le \frac{a+b}{2} \]

可扩展至更一般的形式：

\[a^\theta b^{1-\theta} \le \theta a + (1-\theta)b \]

4.2.2. 常用性质

可微函数的最优性条件
假设凸优化问题的目标函数是可微的，令 \(X\) 表示该问题的可行集，那么 \(x\) 是最优解的充要条件是：

\[\begin{align*} & x \in X, \ and \\ & \forall y \in X, \nabla f_0^T(x) (y-x) \ge 0 \end{align*} \]

4.3. 线性规划问题（LP）

4.4. 线性分式规划（LFP）

4.5. 二次规划（QP、QCQP）

五、对偶

5.1. 拉格朗日对偶函数

5.1.1. 拉格朗日函数

考虑标准形式的优化问题（不一定凸），其中自变量 \(x \in \mathbf{R}^n\)，设问题的定义域是 \(\mathscr{D} = \bigcap_{i=0}^{m} \mathbf{dom} f_i \cap \bigcap_{i=1}^{p} \mathbf{dom} h_i\) 是非空集合，最优值为 \(p^*\)。其形式如下：

\[\begin{align*} minimize & \quad f_0(x) \\ subject \ to & \quad f_i(x) \le 0, i = 1, ..., m \\ & \quad h_i(x) = 0, i = 1, ..., p \end{align*} \]

在此基础上定义拉格朗日函数 \(L(x, \lambda, v): \mathbf{R}^n \times \mathbf{R}^m \times \mathbf{R}^p \rightarrow \mathbf{R}\) 如下。其中 \(\lambda, v\) 称为对偶变量或拉格朗日乘子：

\[L(x, \lambda, v) = f_0(x) + \sum_{i=1}^{m} \lambda_i f_i(x) + \sum_{i=1}^{n} v_i h_i(x) \]

5.1.2. 拉格朗日对偶函数

在此基础上定义拉格朗日对偶函数 \(g(\lambda, v): \mathbf{R}^m \times \mathbf{R}^p \rightarrow \mathbf{R}\) 如下：

\[\begin{align*} g(\lambda, v) & = \inf_{x \in \mathscr{D}} \big{(} L(x, \lambda, v) \big{)} \\ & = \inf_{x \in \mathscr{D}} \big{(} f_0(x) + \sum_{i=1}^{m} \lambda_i f_i(x) + \sum_{i=1}^{n} v_i h_i(x) \big{)} \end{align*} \]

注意，因为拉格朗日函数关于 \(\lambda, v\) 是仿射的（不是 \(x\)），所以对偶函数是关于 \(\lambda, v\) 的一组仿射函数的逐点下确界（凸函数的逐点上确界是凸的，凹函数的逐点下确界是凹的，仿射函数既凸又凹）。也就是说不论原问题的凹凸性，对偶函数一定是凹函数。

下图是一个优化问题的图像示例（其最优解在 \(x = -0.49\)），包含取不同拉格朗日乘子得到的拉格朗日函数：

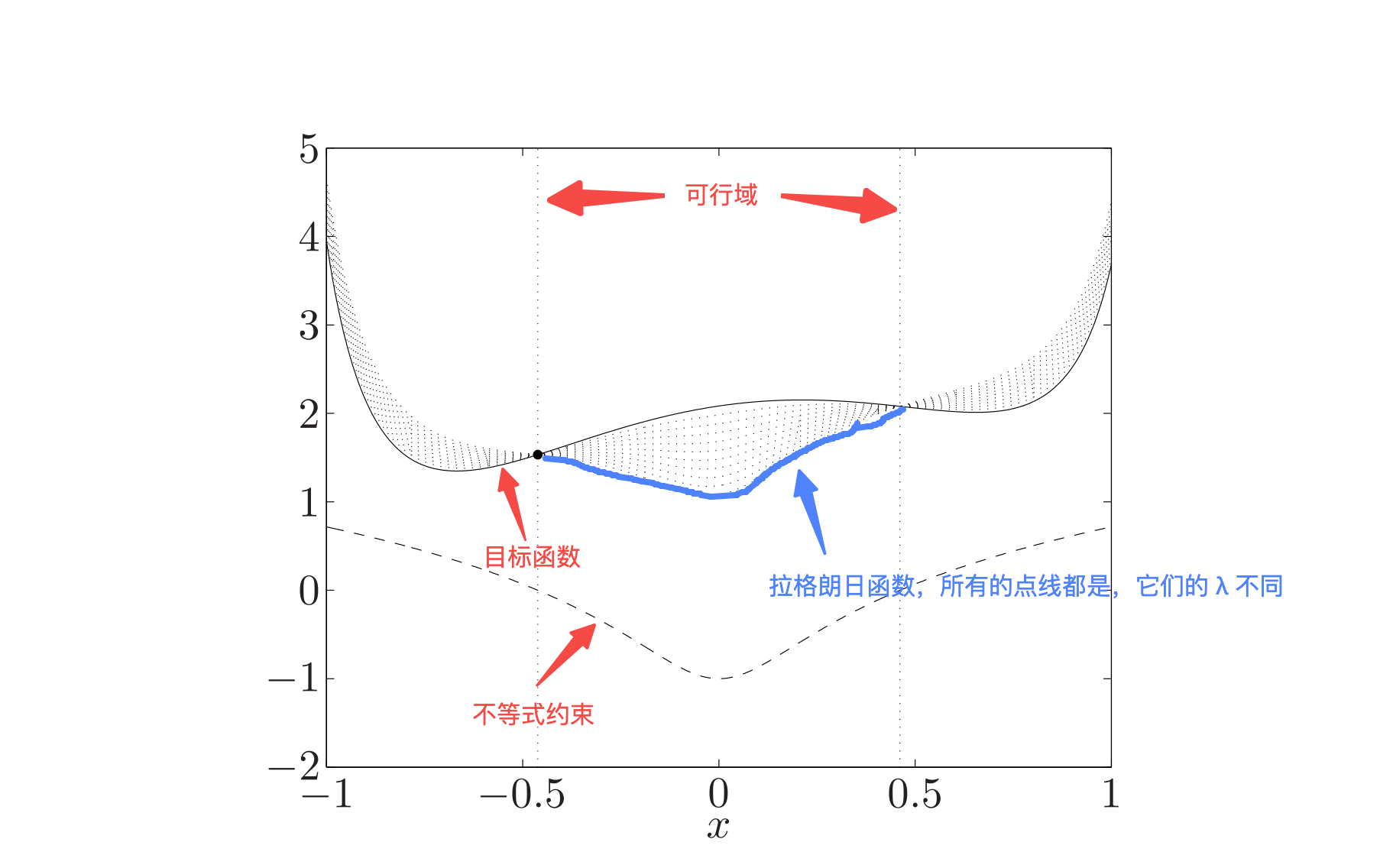
5.1.3. 最优值的下界

对偶函数的最优值（\(d^{*}\)，即最大值），构成了原问题的一个下界（即 \(d^{*} \le p^{*}\)）。很容易理解，因为对于原问题的任意可行解，该解的对偶函数值，必然小于等于该解的拉格朗日函数值（因为逐点下确界）；而拉格朗日函数值又小于等于该解目标函数值（因为约束函数的值是非正的）。即 \(\forall \lambda \succeq 0\) 和 \(v\)，有下式成立：

\[g(\lambda, v) \le p^{*} \]

下图是上图示例， \(x = p^{*} = -0.49\) 时的对偶函数，即关于 \(\lambda\) 的逐点下确界，可以看到图像始终在原问题最优值下方：

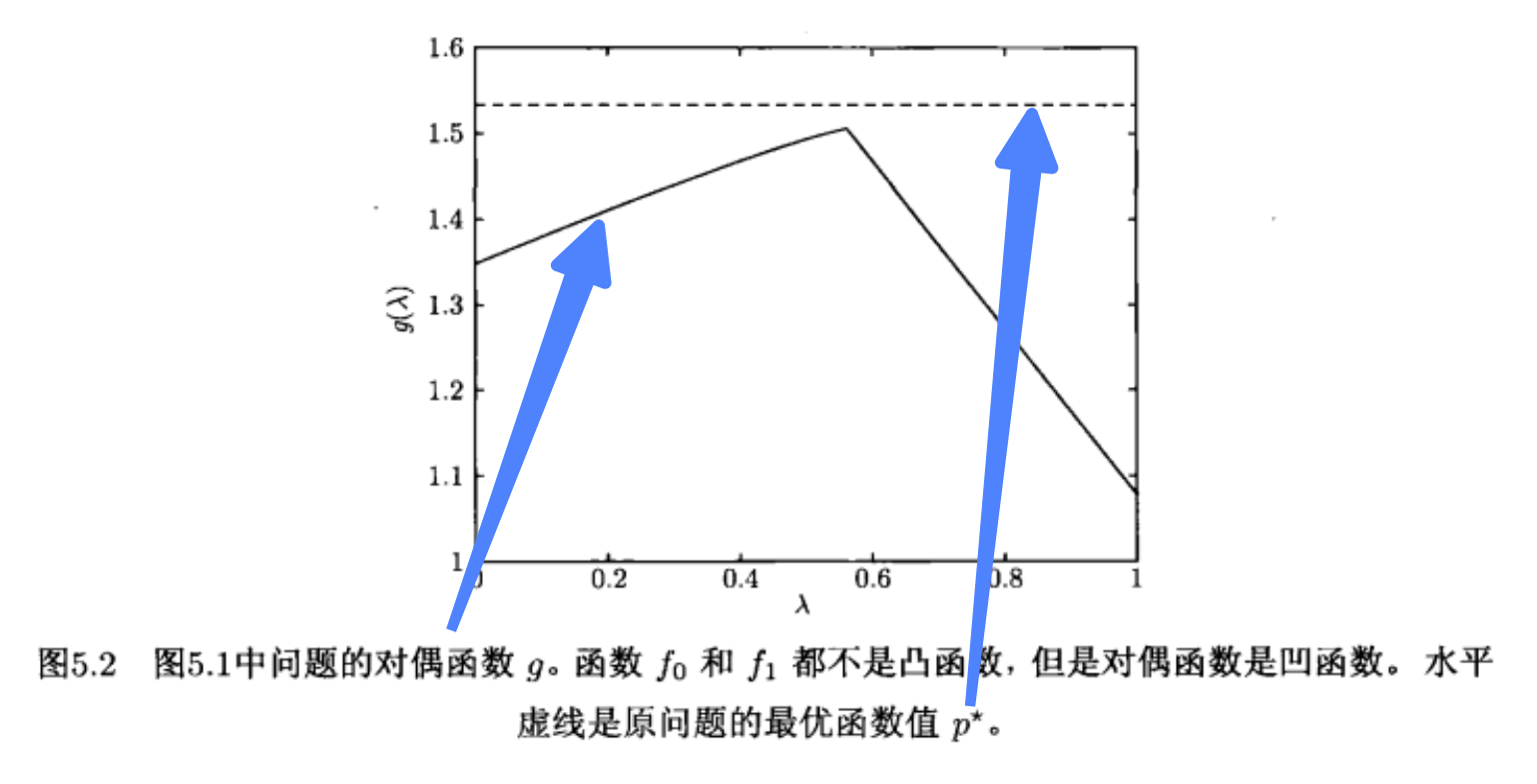
5.1.4. 拉格朗日对偶问题

得到拉格朗日对偶函数之后，对于任意的一组 \((\lambda, v)\)，其中 \(\lambda \succeq 0\)，对偶函数都可以给出原问题最优值 \(p^{*}\) 的一个下界。那么如何从对偶函数得出最好的下界？只需要让这个下界最大化，即最接近原问题最优值，这个问题可表述为如下优化问题：

\[\begin{align*} maximize & \quad g(\lambda, v) \\ subject \ to & \quad \lambda \succeq 0 \end{align*} \]

5.2. 对偶性

5.2.1. 弱对偶性

拉格朗日对偶函数的最优值，即原问题最优值 \(p^{*}\) 的最好下界，记为 \(d^{*}\)。即使原问题非凸，也有 \(d^{*} \le p^{*}\) 成立。这个性质称为弱对偶性。

将差值 \(p^{*} - d^{*}\) 称为原问题的最优对偶间隙，显然其总是非负的。

5.2.2. 强对偶性

如果等式 \(p^{*} = d^{*}\) 即 \(f_0(x^*) = g(\lambda^*, \mathscr{v}^*)\) 成立，即最优对偶间隙为零，则强对偶性成立。如果原问题是凸问题，强对偶性通常（但不总是）成立。而一般情况下，强对偶性不成立。

5.2.3. Slater 条件

相对内部（Relative Interior）

\[\mathbf{relint} \ \mathscr{D} = \{x \in \mathscr{D} \ | \ \exists r > 0, B(x, r) \cap \mathbf{aff}\ \mathscr{D} \subseteq \mathscr{D}\} \]

其中 \(B(x, r)\) 表示以 \(x\) 为中心，\(r\) 为半径的 Euclid 球（\(n\) 维球），\(\mathbf{aff}\ \mathscr{D}\) 表示 \(\mathscr{D}\) 的仿射包。其表示的含义就是，将 \(\mathscr{D}\) 去掉边界后得到的区域。

Slater 条件（对偶性充分条件）

对于如下凸优化问题，如果总是 \(\exists x \in \mathbf{relint} \ \mathscr{D}\)，使得 \(\forall i= 1, ..., m\)，均有 \(f_i(x) < 0, Ax = b\) 成立（不等式约束严格成立），则称 Slater 条件满足：

\[\begin{align*} minimize & \quad f_0(x) \\ subject \ to & \quad f_i(x) \le 0, i = 1, ..., m \\ & \quad A x = b \end{align*} \]

当原问题是凸问题且 Slater 条件成立时，强对偶性成立，即有 \(d^{*} = p^{*}\) 成立。判断 Slater 条件时，不等式约束如果是仿射的，则不要求 “严格小于” 成立。也就是说，如果存在一部分不等式约束是仿射的，即使它们不能严格小于，也不影响 Slater 条件的判定。

5.2.4. 对偶性的几何解释

令原函数和约束函数的函数值集合为：

\[\mathscr{G} = \{ f_1(x), ..., f_m(x), h_0(x), ...h_p(x), f_0(x) \in \mathbf{R}^m \times \mathbf{R}^p \times \mathbf{R} \ | \ x \in \mathscr{D}\} \]

令 \(\mathbf{u} = (f_1(x), ..., f_m(x))^T, \mathbf{v} = (h_0(x), ...h_p(x))^T, t = f_0(x)\)，则原问题最优值 \(p^{*}\) 可表示为：

\[p^{*} = \inf \{ t \ | \ (\mathbf{u}, \mathbf{v}, t) \in \mathscr{G}, \mathbf{u} \preceq 0, \mathbf{v} = 0 \} \]

则拉格朗日函数：

\[L = (\lambda, \mathscr{v}, 1)^T (\mathbf{u}, \mathbf{v}, t) = (\sum_{i=1}^{m} \lambda_i \mathbf{u}_i) + (\sum_{i=1}^{p} \mathscr{v}_i \mathbf{v}_i) + t \]

在 \((\mathbf{u}, \mathbf{v}, t) \in \mathscr{G}\) 上极小化拉格朗日函数，则得到以 \((\lambda, \mathscr{v})\) 为自变量的对偶函数：

\[g(\lambda, \mathscr{v}) = \inf \{ (\lambda, \mathscr{v}, 1)^T (\mathbf{u}, \mathbf{v}, t) \ | \ (\mathbf{u}, \mathbf{v}, t) \in \mathscr{G} \} \]

根据逐点下确界的定义，有 \(L \ge g(\lambda, \mathscr{v})\) 成立，该不等式定义了 \(\mathscr{G}\) 的一个支撑超平面（下图是不包含等式约束，不等式约束也仅有一个的示例，这样可以以图像的方式展示它们之间的关系）：

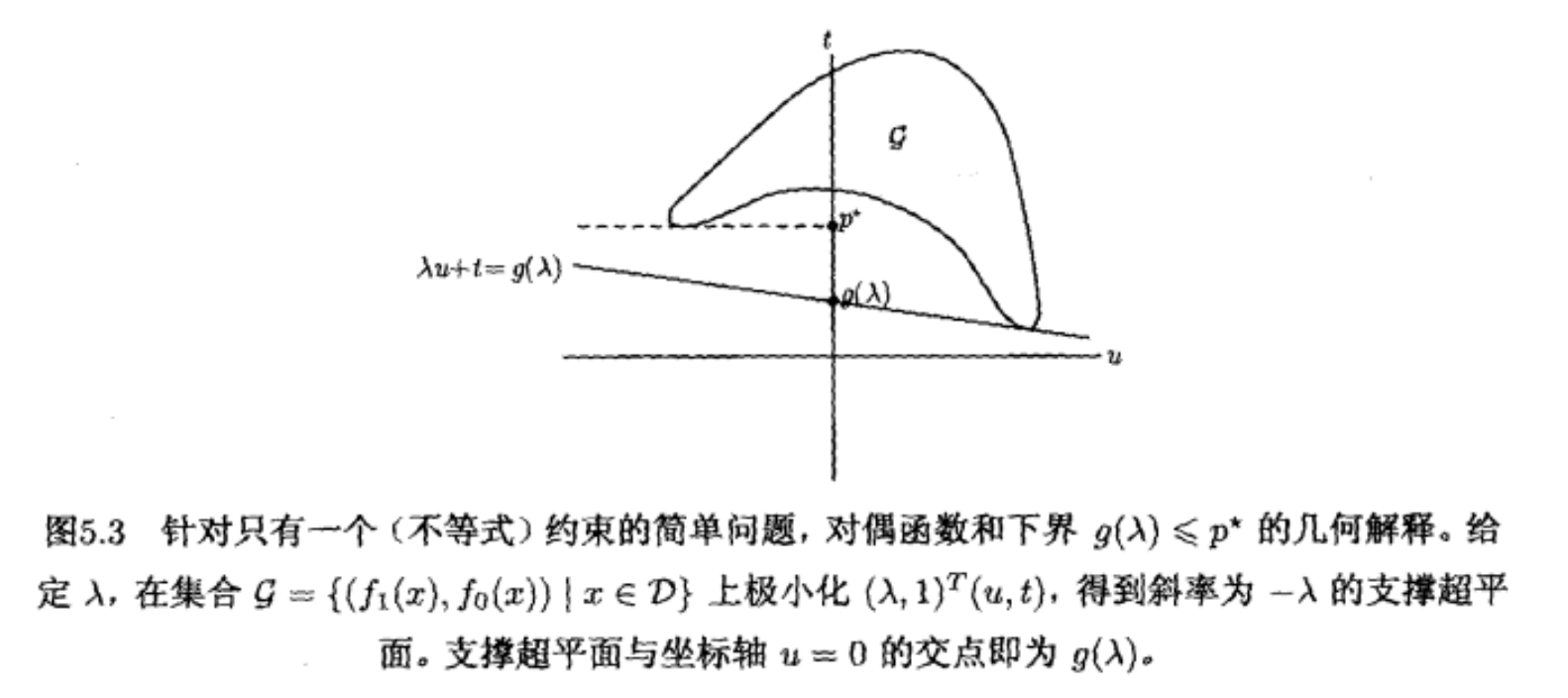
下图为不同 \(\lambda\) 对应的对偶函数：

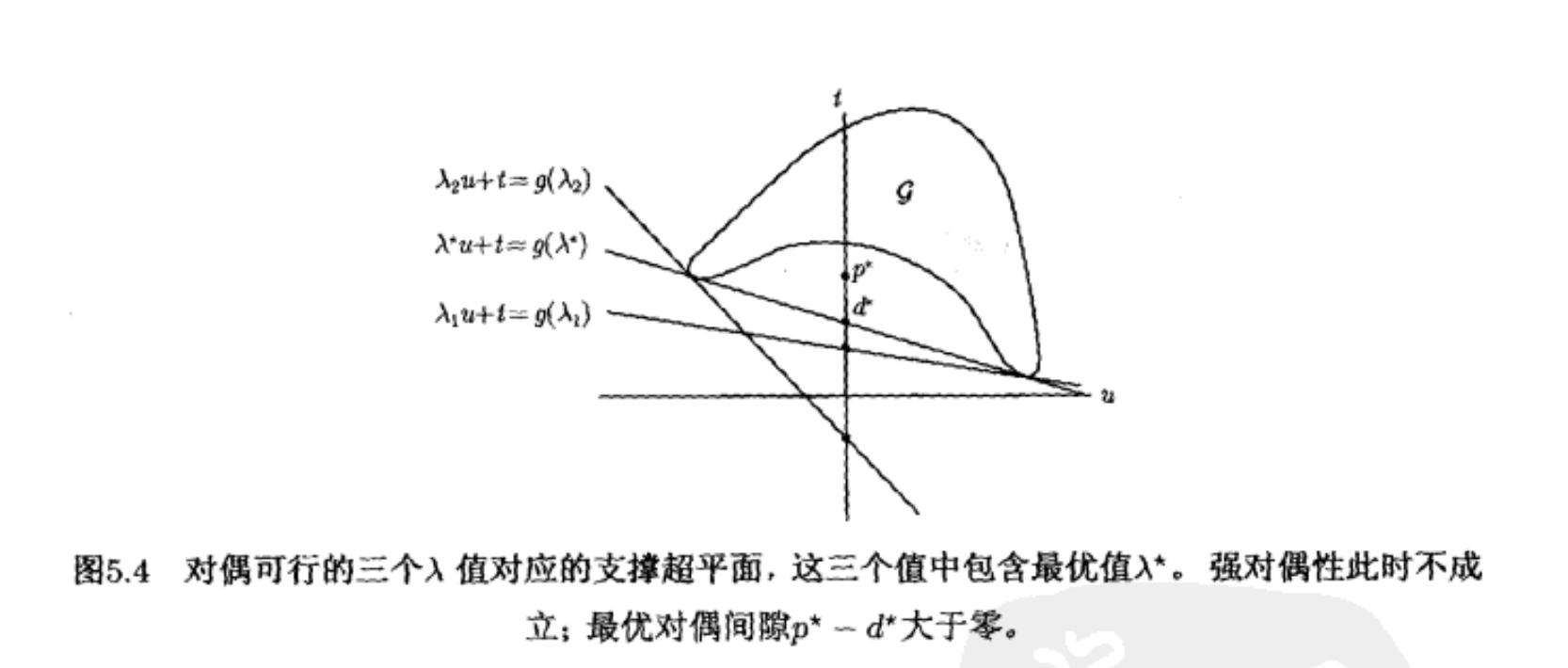
5.2.5. 互补松弛性

假设强对偶性成立，令 \(x^*\) 是原问题的最优解，\((\lambda^*, \mathscr{v}^*)\) 是对偶问题的最优解。则有：

\[\begin{align*} f_0(x^*) & = g(\lambda^*, \mathscr{v}^*) \\ & = \inf_{x} \big{(} f_0(x) + (\sum_{i=1}^{m} \lambda_i^* f_i(x)) + (\sum_{i=1}^{p} \mathscr{v}_i^* h_i(x)) \big{)} \\ & \le f_0(x^*) + (\sum_{i=1}^{m} \lambda_i^* f_i(x^*)) + (\sum_{i=1}^{p} \mathscr{v}_i^* h_i(x^*)) \\ & \le f_0(x^*) \end{align*} \]

显而易见，上述推导过程中的所有不等式均取等号。由此可得：

\[\sum_{i=1}^m \lambda_i^* f_i(x^*) = 0 \mbox{，也即 } \forall i = 1, ..., m, \lambda_i^* f_i(x^*) = 0 \]

此条件称为互补松弛性，它对任意原问题最优解 \(x^*\) 和对偶问题最优解 \((\lambda^*, \mathscr{v}^*)\) 均成立，前提是强对偶性成立。粗略的讲，在最优点 \(x^*\) 处，如果第 \(i\) 个约束起作用了（\(f_i(x) < 0\)），则该项最优拉格朗日乘子一定为零（\(\lambda_i^* = 0\)）。

5.3. KKT 条件

考虑任意优化问题：

\[\begin{align*} minimize & \quad f_0(x) \\ subject \ to & \quad f_i(x) \le 0, i = 1, ..., m \\ & \quad h_i(x) = 0, i = 1, ..., p \end{align*} \]

假设对于该问题：

1. 强对偶性成立，即 \(p^* = d^*\)
2. 所有的函数均可微（原问题、约束，定义域取开集）

对应的对偶函数：

\[g(\lambda, \mathscr{v}) = \inf_{x \in \mathscr{D}} \big{(} f_0(x) + \sum_{i=1}^{m} \lambda_i f_i(x) + \sum_{i=1}^{p} \mathscr{v}_i h_i(x) \big{)} \]

对应的对偶问题：

\[\begin{align*} \max & \quad g(\lambda, \mathscr{v}) \\ subject \ to & \quad \lambda \ge 0 \end{align*} \]

令 \(x^*\) 是原问题的最优解，\((\lambda^*, \mathscr{v}^*)\) 是对偶问题的最优解。

5.3.1. 非凸问题的 KKT 条件

因为 \(L(x, \lambda^*, \mathscr{v}^*)\) 关于 \(x\) 的极小 \(\inf\) 在 \(x^*\) 处取得最小值，因此 \(L\) 在 \(x^*\) 处的导数为零，即：

\[\nabla f_0(x^*) + \sum_{i=1}^{m} \lambda_i \nabla f_i(x^*) + \sum_{i=1}^{p} \mathscr{v}_i \nabla h_i(x^*) = 0 \]

结合其它条件，我们就得到了 Karush-Kuhn-Tucker (KKT 条件)：

\[\begin{align*} & f_i(x^*) \le 0, i = 1, ..., m \\ & h_i(x^*) = 0, i = 1, ..., p \\ & \lambda_i^* \ge 0 \\ & \lambda_i^* f_i(x^*) = 0, i = 1, ..., m \\ & \nabla f_0(x^*) + \sum_{i=1}^{m} \lambda_i \nabla f_i(x^*) + \sum_{i=1}^{p} \mathscr{v}_i \nabla h_i(x^*) = 0 \end{align*} \]

对于目标函数和约束函数可微的任意优化问题，如果强对偶性成立，那么任何一对原问题的最优解和对偶问题最优解必定满足 KKT 条件（必要条件，反之不成立，满足 KKT 条件的点不一定是原问题和对偶问题最优解）。

5.3.2. 凸问题的 KKT 条件

如果原问题为凸问题，且满足强对偶性成立和可微，则 KKT 条件为充要条件。即 KKT 条件成立的点，一定是原问题和对偶问题的最优解。

5.4. 扰动及灵敏度分析

5.4.1. 扰动

考虑对一般优化问题进行扰动后的问题：

\[\begin{align*} minimize & \quad f_0(x) \\ subject \ to & \quad f_i(x) \le u_i, i = 1, ..., m \\ & \quad h_i(x) = v_i, i = 1, ..., p \end{align*} \]

通过控制 \(u_i, v_i\) 的正负，来放松或加强某个约束。令 \(p^*(u, v)\) 为扰动问题关于 \((u, v)\) 的最优值函数，则有 \(p^*(0, 0) = p^*\)。

一个全局不等式
如果强对偶性成立，且对偶问题最优值可取。则对于任意 \(u, v\) 和该扰动问题的最优解 \(x\)（凌青老师是按照 \(x\) 是扰动问题最优解证明的。但书上写的是任意可行解，这里书上写的貌似有点问题），均有如下不等式成立（注意 \(v\) 和 \(\mathscr{v}\) 不一样，前者是扰动，后者是拉格朗日乘子）：

\[\begin{align*} p^*(0, 0) & = g(\lambda^*, \mathscr{v}^*) \\ & \le f_0(x) + \sum_{i=1}^m \lambda_i^* f_i(x) + \sum_{i=1}^p \mathscr{v}_i^* h_i(x) \\ & \le f_0(x) + \lambda^{*T} u + \mathscr{v}^{*T} v \\ & = p^*(u, v) + \lambda^{*T} u + \mathscr{v}^{*T} v \\ & \Downarrow \\ p^*(u, v) & \ge p^*(0, 0) - \lambda^{*T} u - \mathscr{v}^{*T} v \end{align*} \]

上述推论依据：

1. 第一行是根据强对偶性成立即 \(p^* = d^*\) 得到的
2. 第二行是根据对偶函数的定义即 \(\inf\) 性质得到的
3. 第三行是根据扰动约束即 \(f_i(x) \le u_i, h_i(x) = v_i\) 得到的
4. 第四行是扰动最优解的两种表达方式即 \(f_0(x) = p^*(u, v)\)

5.4.2. 灵敏度结论

选择 \((\lambda, \mathscr{v})\) 和 \((u, v)\) 对扰动最优值的影响，由上述不等式得到：

1. \(\lambda_i^*\) 较大时，加强第 \(i\) 个约束，会导致 \(p^*(u, v)\) 大幅增大
2. \(\mathscr{v}_i^*\) 较大且大于零时，选择 \(v_i < 0\)，会导致 \(p^*(u, v)\) 大幅增大
3. \(\mathscr{v}_i^*\) 较大且小于零时，选择 \(v_i > 0\)，会导致 \(p^*(u, v)\) 大幅增大
4. \(\lambda_i^*\) 较小时，放松第 \(i\) 个约束，\(p^*(u, v)\) 不会减小太多
5. \(\mathscr{v}_i^*\) 较小且大于零时，选择 \(v_i > 0\)，\(p^*(u, v)\) 不会减小太多
6. \(\mathscr{v}_i^*\) 较小且小于零时，选择 \(v_i < 0\)，\(p^*(u, v)\) 不会减小太多

5.5. 例子

5.5.1. Boolean LP（布尔线性规划问题）

\[\begin{align*} minimize & \quad c^T x \\ subject \ to & \quad A x \preceq b \\ & \quad x_i \in \{0, 1\}, i = 1, ..., n \end{align*} \]

LP Relaxation

对原问题进行 LP 松弛，即将 \(x_i\) 的离散约束，松弛为一个线性约束，得到新的优化问题。松弛问题更容易求解，且其给出了原优化问题的一个下界：

\[\begin{align*} minimize & \quad c^T x \\ subject \ to & \quad A x \preceq b \\ & \quad 0 \le x_i \le 1, i = 1, ..., n \end{align*} \]

Lagrange Relaxation

将原问题等价表述为以下问题，布尔约束被转化为二次等式约束。通过求解等价问题的拉格朗日对偶问题的最优值，可以得到原问题的另一个下界。通过这种方式求得的原问题最优值下界，称为拉格朗日松弛：

\[\begin{align*} minimize & \quad c^T x \\ subject \ to & \quad A x \preceq b \\ & \quad x_i (1 - x_i) = 0, i = 1, ..., n \end{align*} \]

5.5.2. 罚函数方法

带线性等式约束的凸规划问题

原优化问题如下，其中 \(f_0: \mathbf{R}^n \rightarrow \mathbf{R}\) 且可微，\(A \in \mathbf{R}^{m \times n}, rank A = m\)：

\[\begin{align*} minimize & \quad c^T x \\ subject \ to & \quad A x = b \end{align*} \]

通过引入辅助函数，其中 \(\alpha > 0\) 为参数，\(\alpha \Vert Ax-b \Vert_2^2\) 被称为惩罚项。此方法的思路是寻找辅助函数的最优值 \(\tilde{x}\)，基于这个值找出原问题的对偶问题的一个可行解，再基于这个可行解给出原问题最优值的一个下界：

\[\phi (x) = f_0 (x) + \alpha \Vert Ax-b \Vert_2^2 \]

带线性不等式约束的凸规划问题

原优化问题如下，其中 \(f_0: \mathbf{R}^n \rightarrow \mathbf{R}\) 且可微，\(A \in \mathbf{R}^{m \times n}, rank A = m\)：

\[\begin{align*} minimize & \quad c^T x \\ subject \ to & \quad A x \ge b \end{align*} \]

六、算法