2-1. 算法设计与分析(笔记)
Course:电子科技大学 - 算法设计与分析
Textbook:《Algorithm design》- Jon Kleinberg
ISBN:9780321295354
一、算法基础
1. 问题、算法、程序
Problem
- 一个数学函数,从给定的输入找到匹配的输出
- 一个特定的输入必须始终产生相同的输出结果
- 问题的定义应包含对任何可接受解决方案的可能资源消耗限制
三类问题如:决策问题(yes/no),最优化问题(最佳方案),数值计算
Algorithm
- 通过计算机解决某个问题使用的方法或过程
- 接受一个问题的输入并将其转换为对应的输出
- 一个问题可能有多种算法
Program vs Algorithm
- 程序由电脑读取并执行;而算法是人来设计的
- 程序需要遵守编程语言的规则;算法表示形式更多样,可以是无法执行的伪码或者简单易懂的步骤描述
- 程序一般是算法在某种编程语言下的一个实例或具体表现形式
2. 算法的评价(渐进表达式)
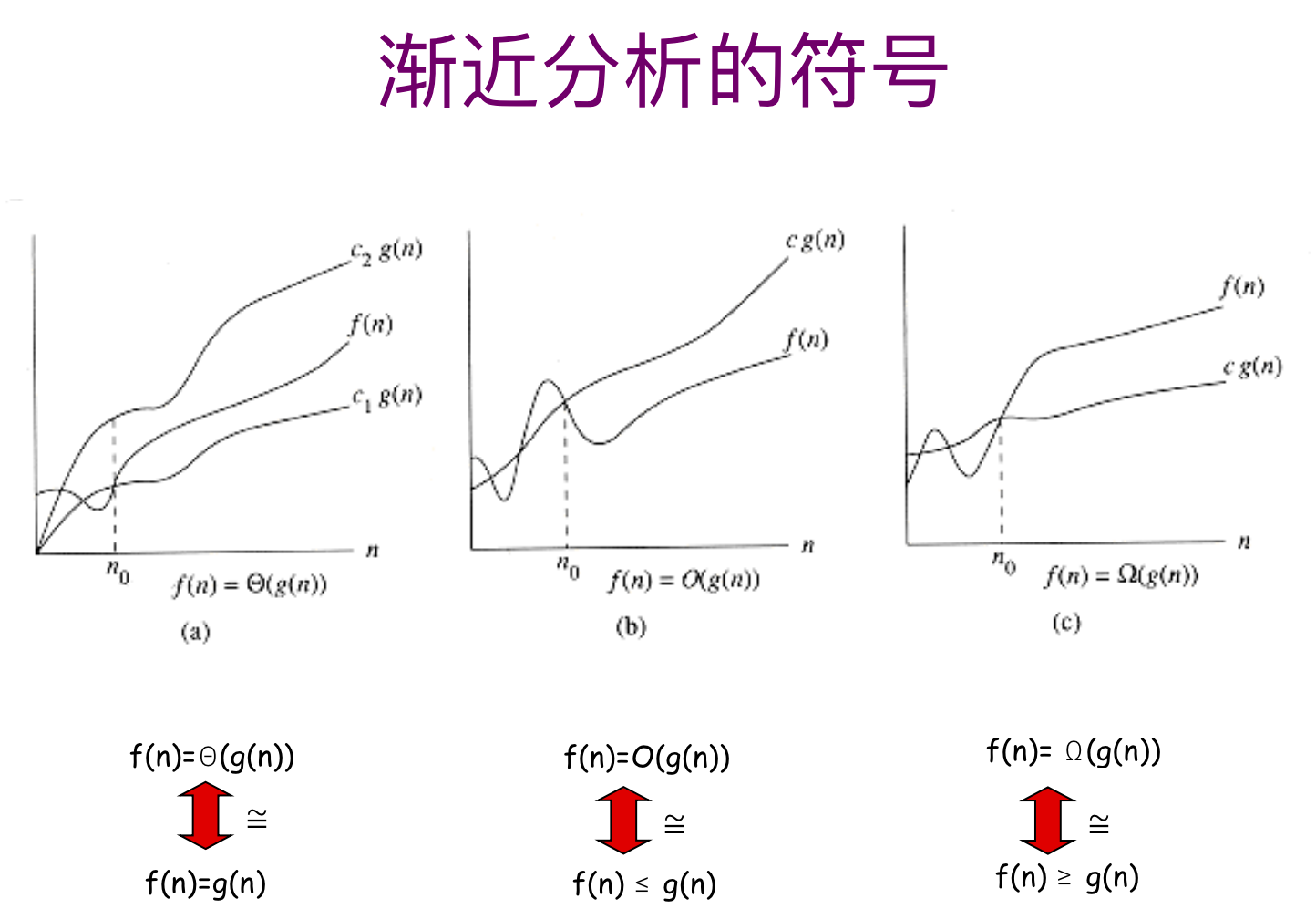
渐进表达式有以下三种,其核心思想都是忽略常数项,关注影响时间或空间的最大因素:
- 渐进上界 \(O\):\(O(g(n)) = \{ f(n) \ | \ \mbox{存在正常数 } c, n_0 \mbox{,使得对于所有 } n \ge n_0 \mbox{,都有 } 0 \le f(n) \le c \cdot g(n) \}\)
- 紧渐进界 \(\Theta\):\(\Theta (g(n)) = \{ f(n) \ | \ \mbox{存在正常数 } c_1, c_2, n_0 \mbox{,使得对于所有 } n \ge n_0 \mbox{,都有 } c_1 \cdot g(n) \le f(n) \le c_2 \cdot g(n)\}\)
- 渐进下界 \(\Omega\):\(\Omega (g(n)) = \{ f(n) \ | \ \mbox{存在正常数 } c, n_0 \mbox{,使得对于所有 } n \ge n_0 \mbox{,都有 } 0 \le c \cdot g(n) \le f(n) \}\)
常见的(渐进上界)时间复杂度
- \(O(1)\):\(f(x) = 12\)
- \(O(\log_{2}n)\):\(f(x) = 3 \log_{2}n + 5\)
- \(O(n)\):\(f(x) = 3n + 5\)
- \(O(n^2)\):\(f(x) = 2n^2 + 5\)
- \(O(n^3)\):\(f(x) = n^3 + 99n^2 + 1000000\)
- \(O(2^n)\):\(f(x) = 3 \cdot 2^n + n^3 + 2n^2 + 1\)
二、排序
...
三、贪心
3.1. 简介
基本思想
选择局部最优解,即在每一步迭代的时候,都选择当前最优解。最终得到的结果便是贪心算法给出的最优结果
特点
- 设计及实现简单
- 部分场景下很高效
- 有可能得到错误或非最优的解
典型应用
- 哈夫曼编码(Huffman Coding)
- 最小生成树算法(Prim,Kruskal)
- 单源最短路径算法(Dijkstra)
- 最小生成树算法
- 最短路径算法
3.2. 活动安排问题(Interval Scheduling)
3.2.1. 问题描述
Q-3.2(问题)
假设有一些时长不等的原子类任务,任务 \(j\) 的起始时间和结束时间分别为 \(s_j, f_j\),其中任意两个任务 兼容 表示它们的执行时间没有重叠。目标:找到相互兼容任务的最大子集。

3.2.2. 贪心模版
将任务按照一定顺序排列(不同的当前最优标准),依次处理每项任务,如果其与已加入结果集的所有任务都兼容,则将其加入结果集中。
- 最早开始时间:按照开始时间 \(s_j\) 升序排列任务
- 最早结束时间:按照结束时间 \(f_j\) 升序排列任务
- 最短执行时间:按照任务长度 \(f_j - s_j\) 升序排列任务
- 最少冲突任务:统计每个任务的冲突任务数,并按照该数值升序排序
3.2.3. 算法
对于问题 Q-3.2 我们考虑使用第二种贪心模版,将每个任务按照结束时间 \(f_j\) 升序排列,依次考察其与已纳入结果集的任务是否冲突。伪代码如下:
Sort jobs by finish times so that f1, f2, ..., fn
A = ∅
for j = 1 to n {
if (job j compatible with A)
A = A ∪ {j}
}
return A
时间复杂度
- 排序:\(O(n \log (n))\)
- 判断当前任务是否兼容:\(O(\log (n))\)
- 循环:\(O(n)\)
综上,贪心算法的总时间复杂度为 \(O(n \log (n))\)
3.2.4. 贪心算法最优性证明
通过反证法证明(假设贪心算法不是最优的推出矛盾):
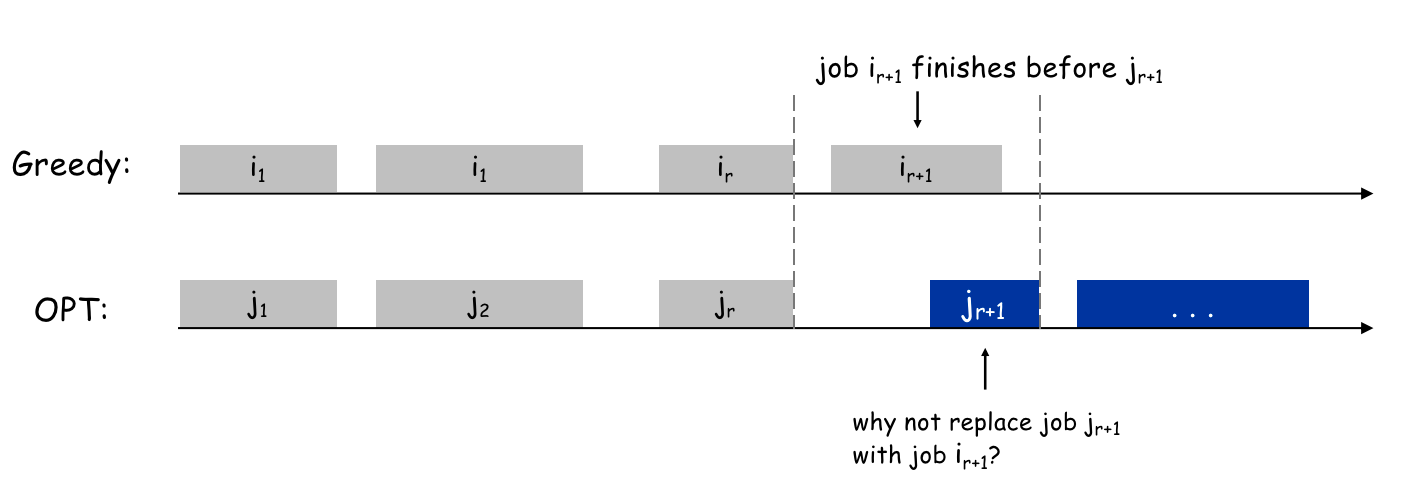
- 上面一行表示贪心算法选择的结果集
- 下面一行是最优的结果集
- 假设前 \(r\) 个任务选择的一致,从 \(r+1\) 个任务开始贪心与最优出现了分歧,即 \(i_{r+1} \neq j_{r+1}\)
- 因为贪心算法选择的是结束时间最早的,那么必有下图的这种情形。此时可推出矛盾,最优算法选择了非最优的结果,因为有 \(i_{r+1}\) 的存在,\(j_{r+1}\) 必然不会是最优选择
3.3. 硬币兑换问题(Coin Changin)
3.3.1. 问题描述
Q-3.3(问题)
给定的硬币面值有:1,5,10,25,100。设计一个算法:对于任意给定的金额,找出使用硬币数量最少的组合,凑出该金额。

3.3.2. 分析
贪心策略
每次迭代添加不超过剩余金额的最大面值硬币,剩余金额初值为总金额,每次添加一个硬币则更新为(剩余金额 = 剩余金额 - 本次添加货币面值)。这个算法是贪心策略,它是最优的吗?
反例
对于如下面值的硬币:1,10,21,34,70,100,350,1225,1500。如果总金额为 140,则有:
- 贪心策略:100 + 34 + 1 + 1 + 1 + 1 + 1 + 1
- 最优解:70 + 70
显然,贪心策略失败了。究其原因,贪心算法得到的解为最优解,需满足如下性质:
- 原问题与子问题具有相同子结构(对剩余金额继续使用贪心策略,与对初始金额使用贪心策略在本质上是一样的)
- 贪心解是可行解(可行解不一定最优)
- 其他解不比当前选择更好(重要!此性质能保证贪心解为最优解)
反例不满足第三条性质,由于 140 与 70 存在倍数关系,导致 100 并不是该阶段的最优解,因此贪心策略失效了。
四、分治
...
五、动态规划
5.2. 背包问题(Knapsack)
5.2.1. 问题描述
Q-5.2(问题)
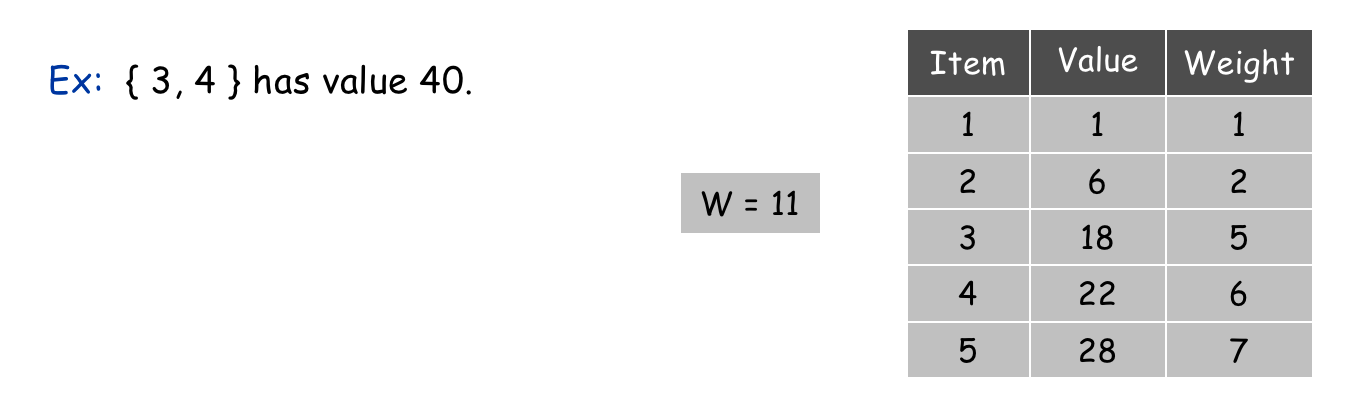
给定 \(n\) 个物品和一个容量为 \(W\) 的背包,每个物品 \(i\) 的价值 \(v_i\) 和重量 \(w_i\) 在表中给定,每个物品最多只能选择 1 次(0-1背包)。使用物品填充背包,要求:设计一个算法求拥有最大价值的填充方案。
5.2.2. 分析
贪心策略
将物品按照单位价值从高到低排序,依次选择填入背包中。最大价值可用 \(\frac{v_i}{w_i}\) 来衡量。注意,按照此贪心策略,上例选择结果为 \(\{5, 2, 1\} = 35\) 非最优解,贪心算法失效了。为了第一次取得最优选择,导致后续的迭代因容量限制而无法选择价值较高的物品。
动态规划思路
定义最佳策略函数 \(OPT(i, w)\),表示在重量为 \(w\) 的限制下,从总共 \(i\) 个物品(\(1, ..., i\))中选出最大价值物品子集。对于第 \(i\) 个物品,OPT 函数有两种可能:
- 没有选择 \(i\) 号物品:OPT 函数递归为在重量 \(w\) 的限制下,从 \(i-1\) 个物品(\(1, ..., i-1\))中选出最大价值物品子集
- 选择了 \(i\) 号物品:OPT 函数递归为在重量 \(w - w_i\) 的限制下,从 \(i-1\) 个物品(\(1, ..., i-1\))中选出最大价值物品子集
综上,我们可以定义递归的 OPT 函数如下:
\(
\begin{aligned}
OPT(i, w) = \begin{cases}
0 & if \ i \ = \ 0 \\
OPT(i-1, w) & if \ w_i \ > \ w \\
\max\{OPT(i-1, w), v_i + OPT(i-1, w-w_i)\} & otherwise
\end{cases}
\end{aligned}
\)
5.2.3. 算法及模拟
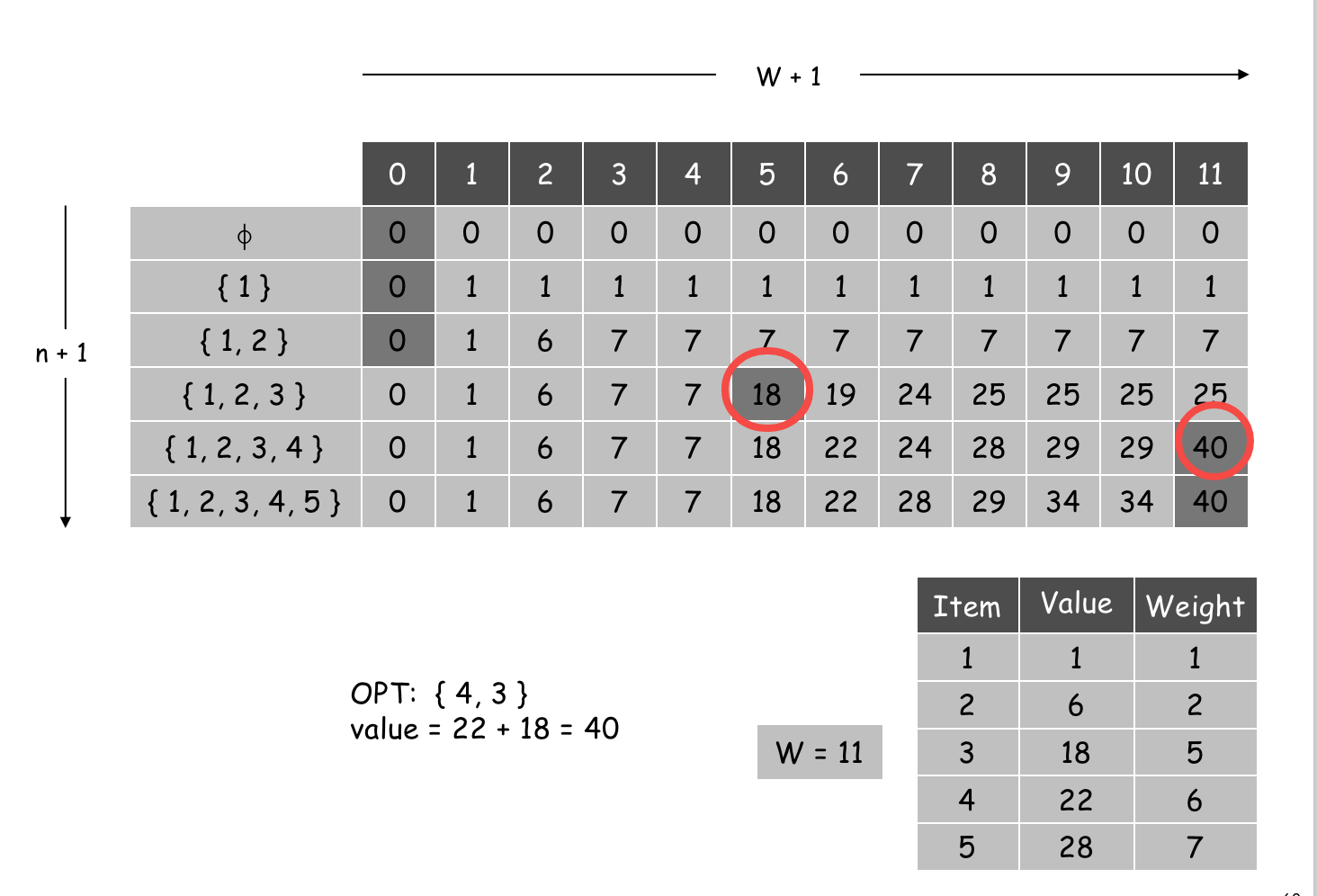
下表为背包问题的动态规划模拟执行表格,横轴为背包的容量(从 0 递增到 11),纵轴为可选的物品集合(从空集递增到全部物品)。
- 原问题背包容量为 11,观察第 11 列,从上往下可以看到最先到达最优价值 40 的物品集合是 \(\{1, 2, 3, 4\}\),即可选物品集合里添加了 4 号物品后得到的价值。因此最优结果集中必选中了 4 号物品。
- 将 4 号物品的重量减去,得到容量为 \(11 - 6 = 5\),观察第 5 列,最先到达最优价值 18 的物品集合是 \(\{1, 2, 3\}\),即可选物品集合里添加了 3 号物品后得到的价值。因此最优结果集中必选中了 3 号物品。
- 再将 3 号物品的重量减去容量已经为 0,则最优集为 \(\{3, 4\} = 40\)。
上述表格亦可描述为一棵二叉树,其深度与物品个数相同,最终对比叶子结点的大小,则从根节点至该叶子结点的路径,即为物品选择的最佳方案:
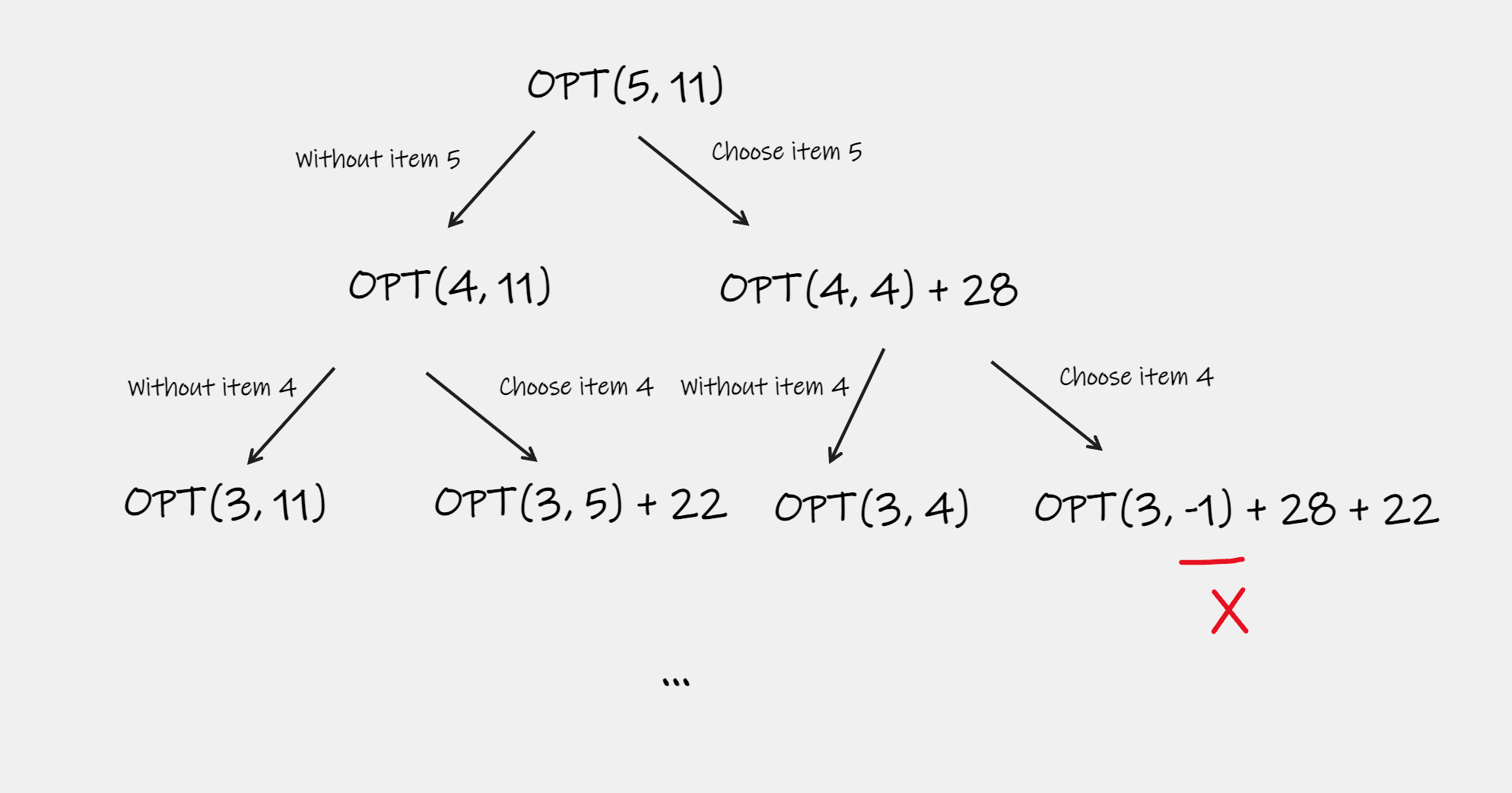
5.3. 对比
5.3.1. 动态规划 vs 贪心
动态规划和贪心算法都是一种递推算法,均有最优子结构性质,通过局部最优解来推导全局最优解。
两者之间的区别在于:贪心算法中作出的每步贪心决策都无法改变,因为贪心策略是由上一步的最优解推导下一步的最优解,而上一部之前的最优解则不作保留,贪心算法每一步的最优解一定包含上一步的最优解(一条道走到黑)。动态规划算法中全局最优解中一定包含某个局部最优解,但不一定包含前一个局部最优解,因此需要记录之前的所有最优解(可以把动态规划理解为一种优化的暴力算法,会产生很多可行解但又不会像暴力算法一样做很多无效操作)。
5.3.2. 动态规划 vs 分治
动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,最终达到解决原问题的效果。
但不同的是,分治法的子问题可能被重复计算了很多次,而动态规划则具有记忆性,通过填写表把所有已经解决的子问题答案纪录下来,在新问题里需要用到的子问题可以直接提取,避免了重复计算,从而节约了时间。
六、其它问题
6.1. 最大流问题(Maximum flow problem)
6.1.1. 背景
实际的应用场景中,“流网络” 有如下类似的场景:
- 道路交通网:人、车在道路上的流动
- 供水网:水在管道中的流动
- 互联网:网络信号在物理层设备间的流动
- 金融系统网:钱在账户之间的流
以道路交通网为例,考虑如下实际问题:将道路交通图模型化为一个有向图,以此寻找从某一个城市出发,到另一个城市之间的最短路径。这便是最大流所要解决的问题:如何充分利用通道,使得整个网络传输的流量最大,以取得最好的效果。这是一种典型的组合最优化问题。
其算法最早由福特和福克逊于1956年提出,20世纪50年代福特(Ford)、福克逊(Fulkerson)建立的“网络流理论”,是网络应用的重要组成成分。
6.1.2. 问题抽象
Q-6.1(问题)
定义有向图 \(G=(V, E)\),其中 \(V\) 为顶点集,\(E\) 为边集,有序对 \((s, t)\) 表示从顶点 \(s\) 到顶点 \(t\) 的路径。其中 \(c(e)\) 表示边 \(e\) 能够通过的最大流量(Capacity),\(f(e)\) 表示边 \(e\) 的实际流量(flow),\(fin(v)\) 和 \(fout(v)\) 分别表示结点 v 实际流入和流出的流量。求满足约束的从起点 \(s\) 到终点 \(t\) 的最大流(MaxFlow),最大流的定义即最终流入终点 \(t\) 的总流量,也是起点流出的总流量。问题中的约束如下:
- \(0 \le f(e) \le c(e)\),即任意边的实际流量总是小于等于最大容量
- \(\forall v \in V, v \ne s, v \ne t, \mbox{ 都有 } fin(v) = fout(v)\),即除起点和终点外,中间节点的流入和流出流量保持相等
Def(定义)
- \(s-t \ cut\):将顶点集 V 分为 (A, B) 两部分,其中 \(s \in A, t \in B\),且原图去掉割集中包含的边后,从 \(s\) 到 \(t\) 无连通路径
- \(cap(A, B)\):割集 (A, B) 的容量,即 \(\sum\limits_{e \ out \ of \ A} c(e)\)
Theorem(定理)
1. 最大流等价于最小割
最小割的流量等于最大流 f 的流量
因为若 f 不是最大流
则一定能找到不属于 f 的边,使其能构成新的连通路径到达 t,才能增加流量值
但因为去掉最小割的任意边后,图已经不连通
所以最小割的边集合已经全在流 f 中
则添加非最小割边不能改变图的连通性
即目前已经无法增加流量
所以最小割对应的流的流量已经达到最大,即最大流
6.1.3. 模拟解法
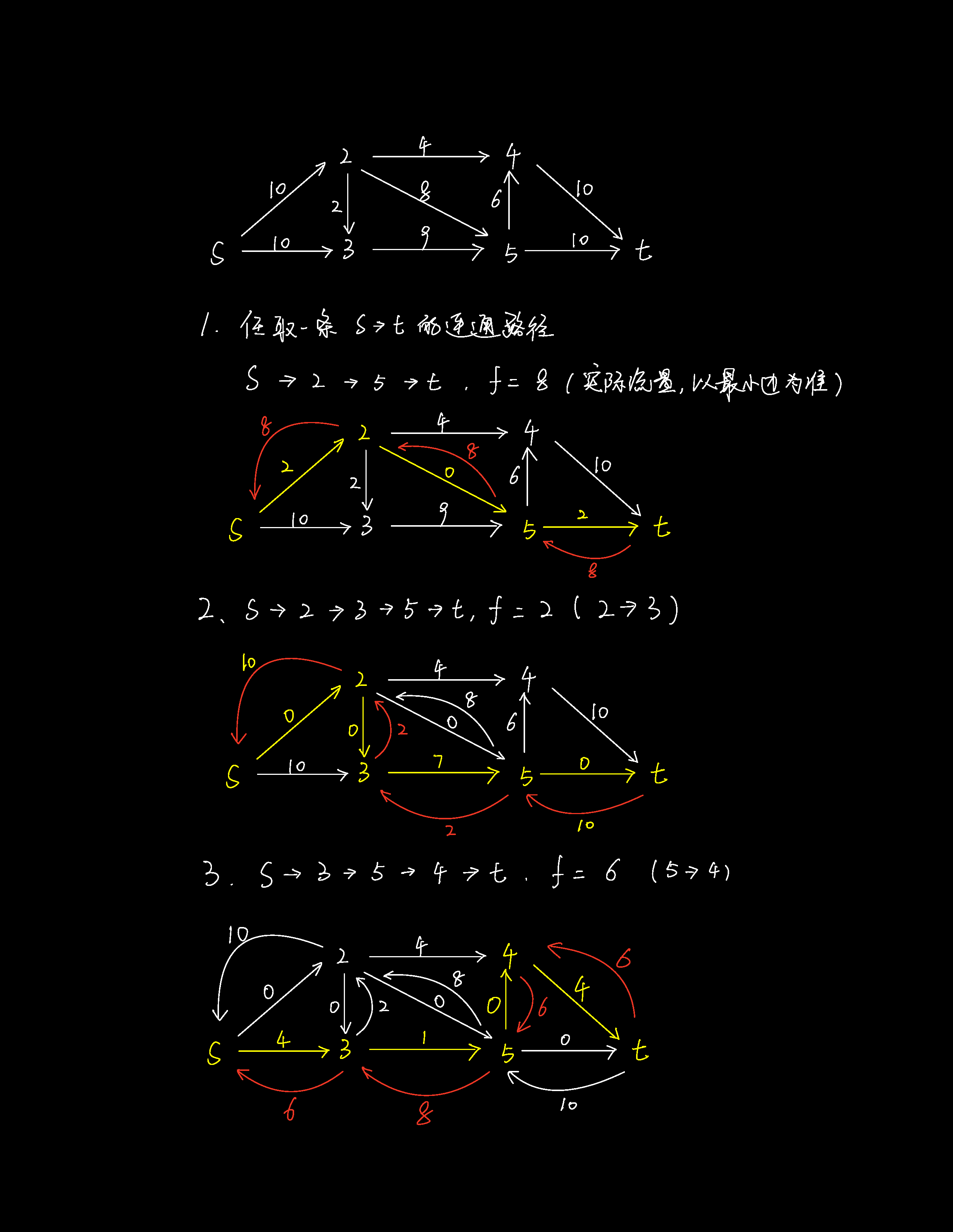
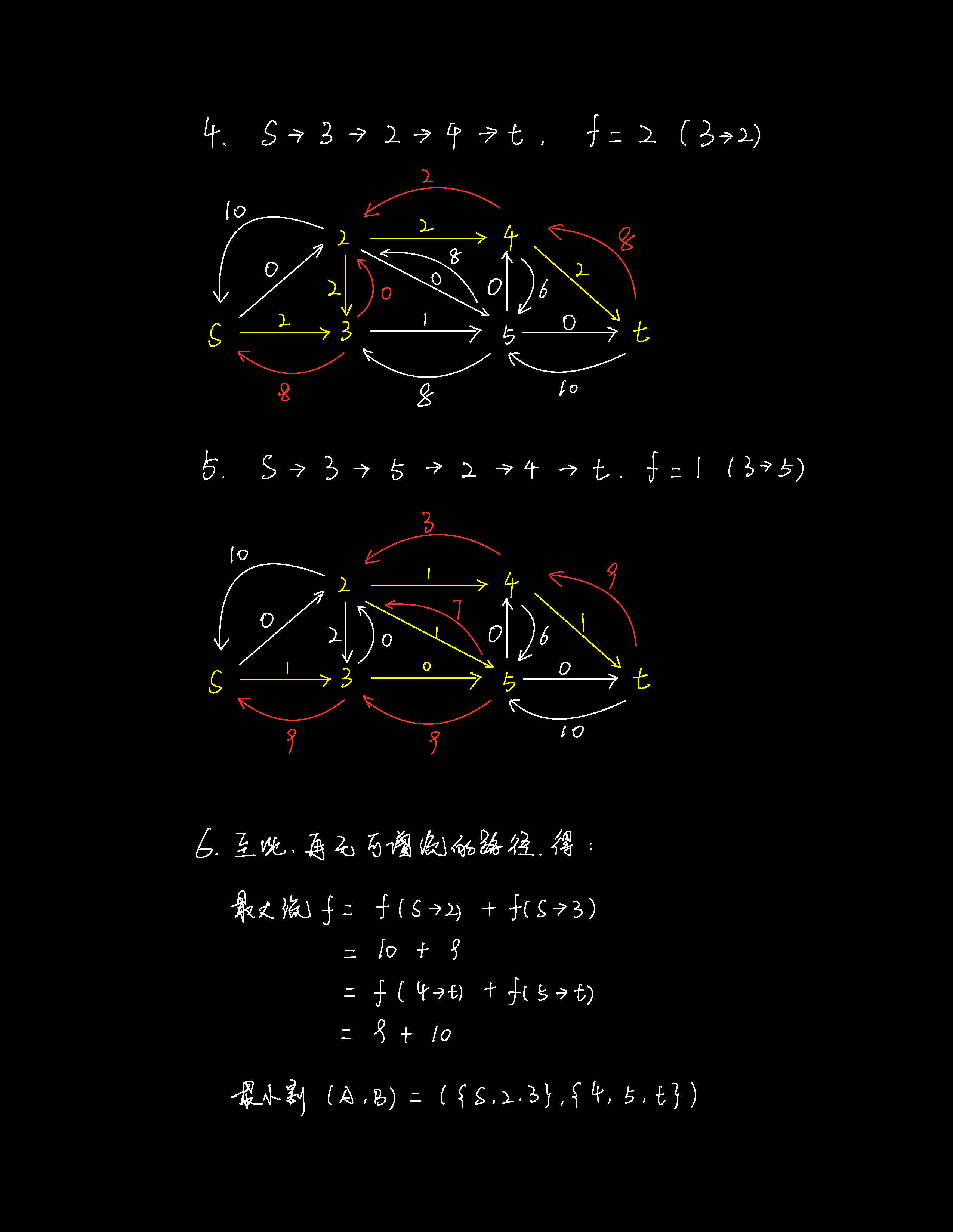
6.2 NP 完备性理论
6.2.1. 多项式时间归约
问题 X 可以在多项式时间归约到问题 Y,当且仅当问题 X 可以被解决:
- 通过多项式次的标准运算步骤,加上
- 多项式次对问题 Y 的解法的调用
记作 \(X \le_p Y\)
Theorem(定理)
- 如果 \(X \le_p Y\),且 \(Y\) 可以在多项式时间内解决,那么 \(X\) 也可以在多项式时间内解决
- 如果 \(X \le_p Y\),且 \(X\) 不能在多项式时间内解决,那么 \(Y\) 也不能在多项式时间内解决
- 如果 \(X \le_p Y\),且 \(Y \le_p X\),则 \(X\) 和 \(Y\) 等价
6.2.2. (最大)独立集问题
给定一个无向图 \(G = (V, E)\) 和整数 \(k\),是否存在一个顶点集的子集 \(S \in V\) 且 \(|S| \ge k\)。使得图中任意一条边,至多有一个端点在集合 \(S\) 中?
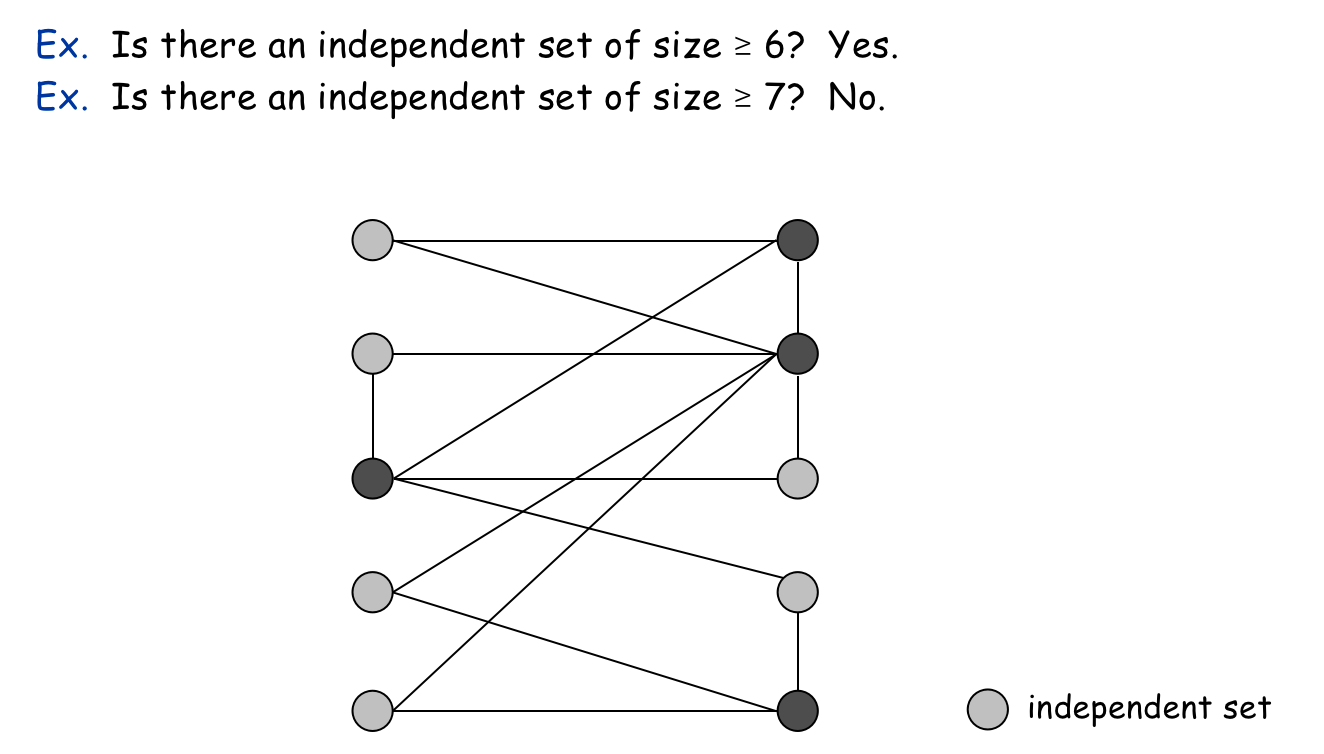
6.2.3. (最小)点覆盖问题
给定一个无向图 \(G = (V, E)\) 和整数 \(k\),是否存在一个顶点集的子集 \(S \in V\) 且 \(|S| \le k\)。使得图中任意一条边,至少有一个端点在集合 \(S\) 中?

Proof(证明)
最大独立集问题等价于最小点覆盖问题,即如果 \(S\) 是一个最大独立集,那么 \(V-S\) 是最小点覆盖。

6.2.4. 最大团问题
给定无向图 \(G = (V, E)\)。如果 \(U\) 是 \(V\) 的一个子集,且对任意 \(u, v \in U\) 有 \((u, v) \in E\),则称 \(U\) 是 \(G\) 的完全子图
- \(G\) 的完全子图 \(U\) 是 \(G\) 的团当且仅当 \(U\) 不包含在 \(G\) 的更大的完全子图中,即 \(U\) 就是最大完全子图
- \(G\) 的最大团是指 \(G\) 中所含顶点数最多的团
特别的,原图的最大独立集等价于补图的最大团,因此二者可以相互归约
6.2.5. 集合覆盖问题
问题描述
假设有一个集合 \(A\),其中包含了 \(m\) 个不同元素,现有 \(n\) 个集合,分别为 \(B_1, B_2, ..., B_n\),且 \(B_1 \cup B_2 \cup ... \cup B_n = A\)。问题:是否存在 \(B\) 集合的最小子集,使得它们的并集也等于 \(A\) 集合?
例如:\(A = \{1, 2, 3, 4, 5\}\),集合\(B = \{\{1, 2, 3\}, \{2, 4\}, \{3, 4\}, \{4, 5\}\}\)。可以看出,\(B\) 集合的并集恰好等于 \(A\) 集合,集合覆盖为 \(SETCOVER = \{\{1, 2, 3\}, \{4, 5\}\}\)。
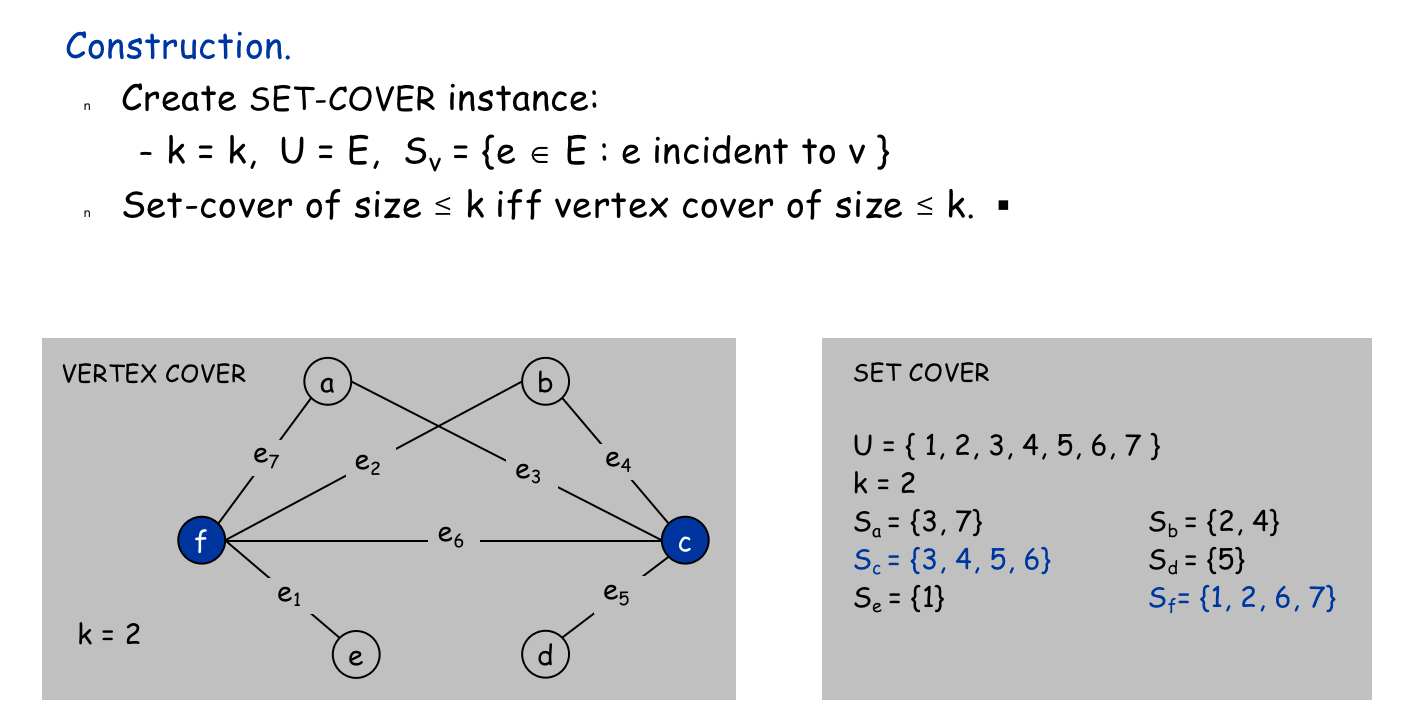
Proof(证明)
\(Vertex-Cover \le_p Set-Cover\),即点覆盖问题可以多项式时间归约到集合覆盖问题(通过点覆盖构造集合覆盖)
- \(k\):点覆盖中点的个数
- \(U\):原图的边集
- \(S_v\):原图中所有与顶点 \(v\) 相连的边
- 集合覆盖:设点覆盖中的点为 \(i\),则 \(S_i\) 在集合覆盖中
6.2.6. 3-SAT 问题
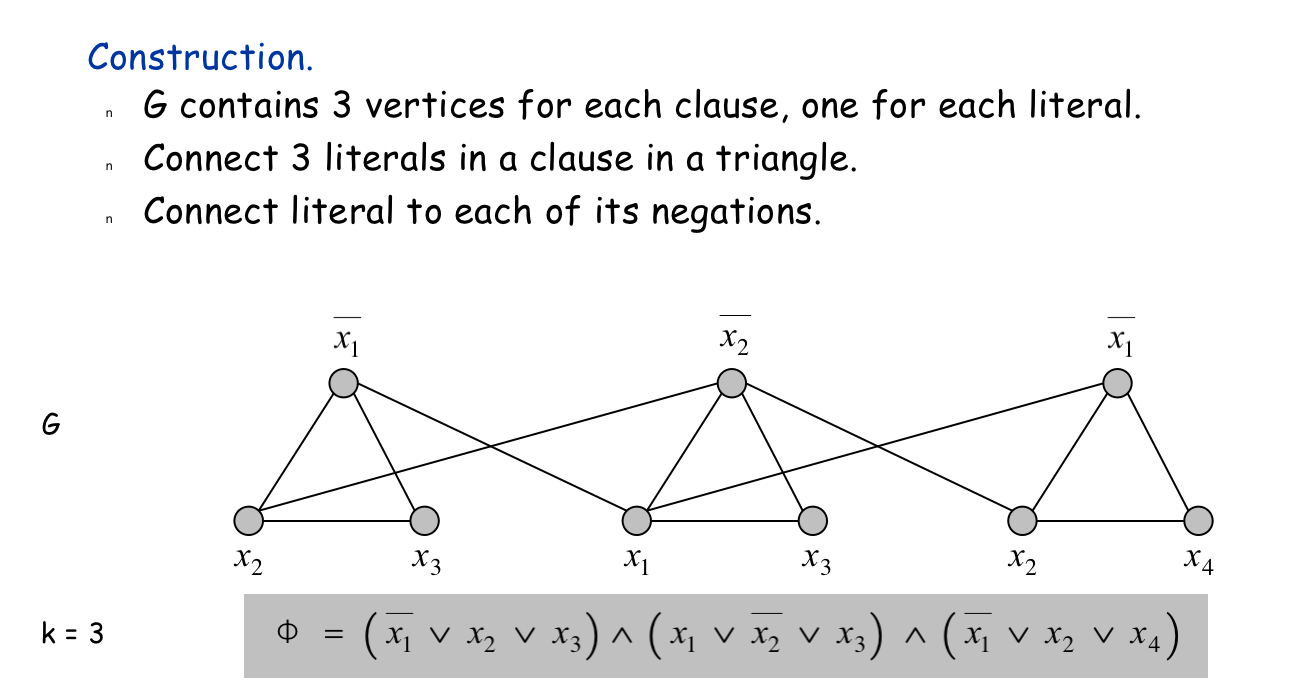
Proof(证明)
\(3-SAT \le_p Independent-Set\),即 3SAT 问题可以多项式时间归约到独立集问题
- 每个子句(括号)建立为一个全相连的图,子句内的每个元素作为图中一个顶点
- 将每个顶点与其否定词相连接
综上,有如下规约关系:\(3-SAT \le_p Independent-Set \le_p Vertex-Cover \le_p Set-Cover\)
6.2.7 自归约
将求解问题归约成判断问题,如果判断问题能够解决,那么就可以利用判断问题来解决求解问题。
比如最小点覆盖问题,假如我们能判断一个图中是否存在点数为 \(k\) 的最小点覆盖。那么可以遍历图中的每个顶点,删去这个顶点以及和这个顶点相连接的边,图中若只存在点数为 \(k-1\) 的点覆盖,那么就可以判定该顶点是最小点覆盖中的顶点,不断重复这个操作,就可以找到最小点覆盖。
6.3 NP
定义
- P 问题:存在多项式时间算法的决策问题(多项式时间可解的问题)
- EXP 问题:存在指数时间算法的决策问题
- NP:多项式时间可以验证的决策问题(给定一个解,可以多项式验证其可行性)
- NPC 问题:指某个有特殊性质的 NP 问题 \(Y\),即对于任意的 NP 问题 X,都有 \(X \le_p Y\)
证明 NPC 问题
- 首先证明该问题是 NP 问题(多项式时间可验证)
- 选择一个 NPC 问题,作为 X
- 证明 X 可以多项式时间归约到该问题
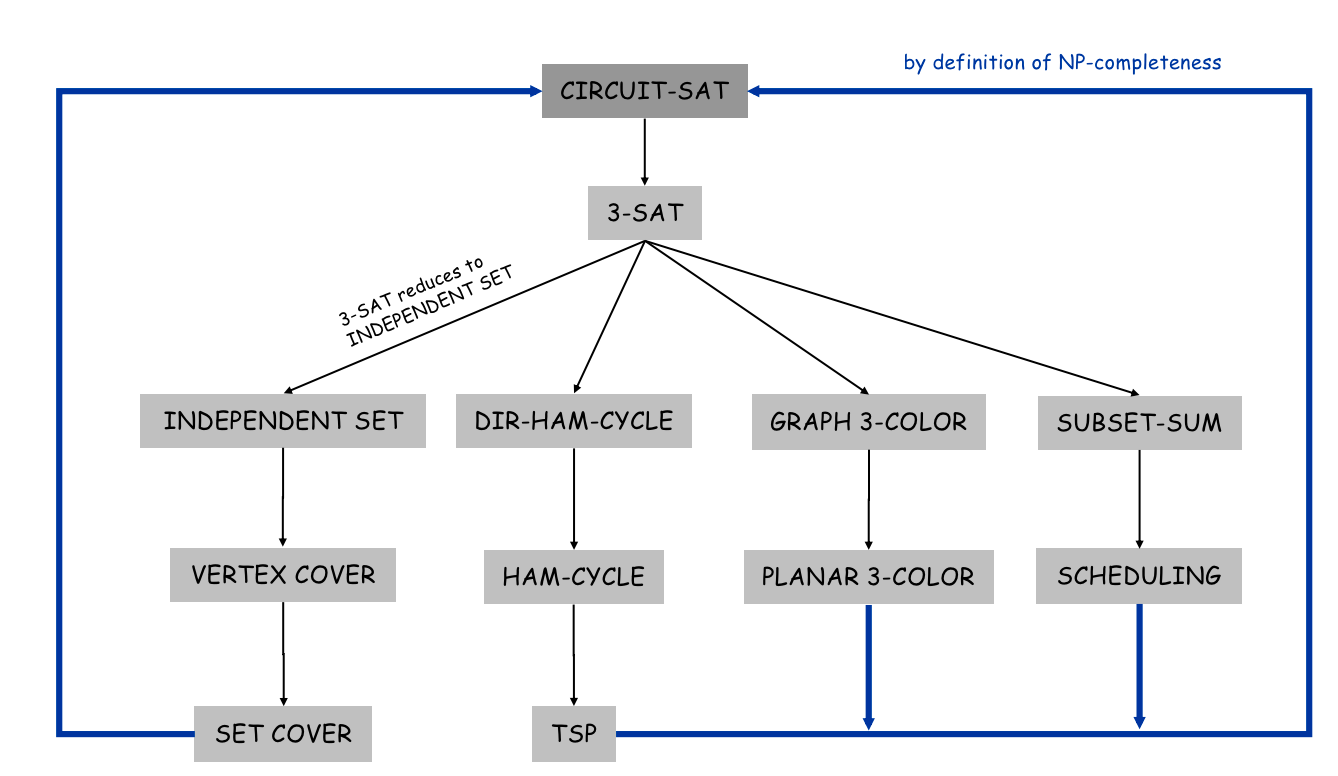
下图是常见的 NPC 问题:
6.4 近似算法
定义
近似算法关注的三个方面:
- 解的优越性,即是否能达到最优解
- 算法的效率,即复杂度(能否在多项式时间内完成)
- 算法适用的范围,即是否适用于所有情况,还是只适合特殊情形
一般的算法在这三个方面往往不能同时表现得很好,但是我们可以退而求其次,选择其中得两个方面去尽可能地满足,当我们选择满足后两者,即对解的优越性放宽要求时,设计出的算法被称为近似算法。

