图
一、学习总结
1.1思维导图
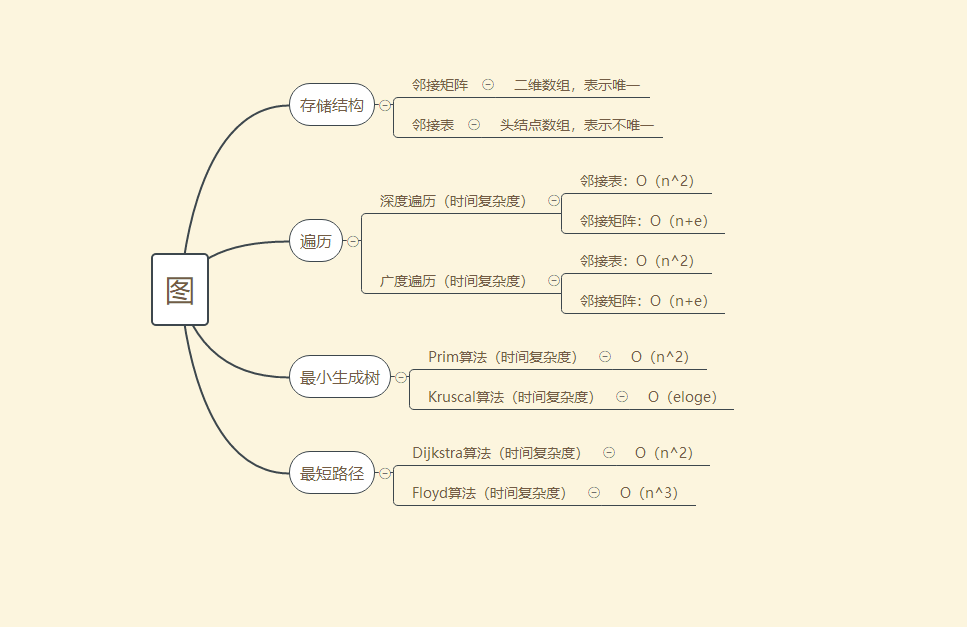
1.2 学习体会
深度遍历算法：首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点。
广度遍历算法：从一个顶点V0开始，辐射状地优先遍历其周围较广的区域。可以解决广度优先生成树，最短路径等问题。
Prim和Kruscal算法：Prim适用于邻接矩阵储存和较密的图，Kruscal算法适用于邻接表储存和较稀疏的图
Dijkstra算法：Dijkstra算法用来求最短路径
拓扑排序算法：对于任何连接自顶点u到顶点v的有向边uv，在最后的排序结果中，顶点u总是在顶点v的前面。
二、PTA实验作业
题目一： 图的着色问题
设计思路
while（n--）
{
for i=1 to 顶点数
输入颜色方案
判断颜色数目是否与k相等，若不等flag=0
将颜色按深度遍历排序储存在数组e中
for i=0 to 顶点数
for j=0 to 顶点数
如果g->a[d[i]][d[j]]==1
令flag=0且退出循环
如果flag=0
输出no 否则 输出yes
}
代码截图
PTA提交列表说明。
题目二：排座位
设计思路
建图
对visited[][]进行初始化为0
若friends[a][b]==1
则为朋友关系，输出“No problem”
对a,b检查是否存在共同的朋友
若存在，flag=1
若不存在，则flag=0；
if（是敌人关系）{
存在共同朋友
输出"OK but..."
否则输出“No way”
}
else（不是朋友也不是敌人）{
存在共同朋友，输出"No problem"
否则输出“OK”
}
代码截图
PTA提交列表说明。
题目三：
设计思路
while（队列不为空）{
将number置为队列头元素，删除队列头元素；
遍历顶点i=0 to i<N{
若visited[i]==0且G[number][i]==1；
将i进队，visited[i]置为1，记录节点数
}
}
若访问到该层的最后一个节点
层数加一，改变访问的最后一个节点
层数达到6结束，返回记录的节点数
代码截图
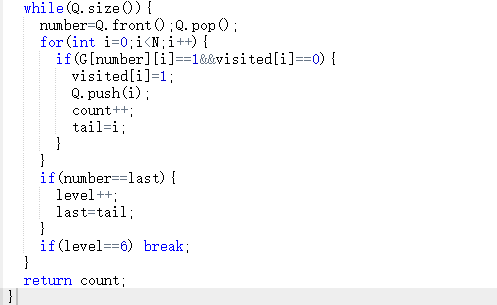
PTA提交列表说明。
三、截图本周题目集的PTA最后排名
总分：2
