傅里叶变换的简易证明

傅里叶变换FT

傅里叶级数：法国数学家傅里叶发现，任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。

1.三角函数正交性

三角函数正交性用到了：\((i)\)三角函数系 \((ii)\) 三角函数的积化和差 \((iii)\) 向量内积

1.1三角函数系

三角函数系就是由下列具有一定规律的正弦函数、余弦函数组成的集合：

\[0,1,sinx,cosx,sin2x,cos2x,\dots sinnx,cosnx,\dots \tag{1.1.1} \]

所谓的三角函数的正交性，就是集合中任意两个不同函数乘积在\([-\pi,\pi]\) 上的积分为 \(0\)。证明需要用到三角函数的积化和差公式。

1.2三角函数的积化和差

\[sin\theta cos\beta = \frac{1}{2}(sin(\theta +\beta) + sin(\theta - \beta)) \\ cos\theta sin\beta = \frac{1}{2}(sin(\beta+\theta) + sin(\beta - \theta)) \\ cos\theta cos\beta = \frac{1}{2}(cos(\theta +\beta) + cos(\theta - \beta)) \\ sin\theta sin\beta = \frac{1}{2}(cos(\theta -\beta) - cos(\theta + \beta)) \\ \tag{1.2.1} \]

1.3向量内积

假设\(\vec{a}=(a_1,a_2,a_3,a_4,\dots,a_n) \quad \vec{b}=(b_1,b_2,b_3,b_4,\dots,b_n)\)

如果两个向量正交则：\(\vec{a} ·\vec{b} = a_1b_1+a_2b_2+a_3b_3+\dots+a_nb_n = \sum_{i=1}^{n}a_ib_i = 0\)

如果将这种正交的概念拓展到函数当中，我们假设\(f(x) = a\quad g(x) =b\)：$$f(x)·g(x) =b\int_{x_0}^{x_1} f(x)g(x)dx = 0 $$

我们假设\(f(x)\)和\(g(x)\)分别是三角函数系中的两个不同的三角函数，则可以证明三角函数的正交性：

\[\begin{align*} \int_{-\pi}^{\pi}cos nxdx = \frac{1}{n}sin nx|^{\pi}_{-\pi} = 0 \tag{1.3.1} \\ \int_{-\pi}^{\pi}sin nxdx = -\frac{1}{n}cos nx|^{\pi}_{-\pi} = 0 \tag{1.3.2} \\ \int_{-\pi}^{\pi}sin nx \space cosmx \space dx = \frac{1}{2}\int_{-\pi}^{\pi}[sin(n+m)x + sin(n-m)x]dx = 0\tag{1.3.3}\\ \int_{-\pi}^{\pi}sin nx \space sinmx \space dx = \frac{1}{2}\int_{-\pi}^{\pi}[cos(n-m)x-cos(n+m)x]dx = 0\tag{1.3.4}\\ \int_{-\pi}^{\pi}cos nx \space cosmx \space dx = \frac{1}{2}\int_{-\pi}^{\pi}[cos(n+m)x+cos(n-m)x]dx = 0\tag{1.3.5}\\ \int_{-\pi}^{\pi}cos nx \space cos nx dx = \int_{-\pi}^{\pi}cos^2 nxdx = \int_{-\pi}^{\pi}\frac{1}{2}(1+cos2x)dx = \pi \tag{特殊} \\ \int_{-\pi}^{\pi}sin nx \space sin nx dx = \int_{-\pi}^{\pi}sin^2 nxdx = \int_{-\pi}^{\pi}\frac{1}{2}(1-cos2x)dx = \pi \tag{特殊} \end{align*} \]

2.周期为\(2\pi\)的傅里叶级数展开

\[f(x) = \sum_{n=0}^{\infty}(a_n\cos{nx}+b_n\sin{nx}) = a_0 + \sum_{n=1}^{\infty}(a_n\cos{nx}+b_n\sin{nx}) \tag{2.1.1} \\a_0 = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx \quad\quad a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos{nx}dx \quad\quad b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin{nx}dx \]

证明过程：

2.1 Step1:找\(a_0\)

我们对\(f(x)\)求积分：\(\int_{-\pi}^{\pi}f(x)dx = \int_{-\pi}^{\pi}{ a_0 }dx + 0 + 0\rightarrow a_0 = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx\)

2.2 Step2: :找\(a_n\)

要想求得 \(a_n\) 则需要去除无关变量\(a_0\) 和\(b_n\) ，根据三角函数正交性，当我们乘以一个 \(\cos{nx}\) 的时候\(a_0\) 和\(b_n\) 项积分之后都是 \(0\) ，但是我们得乘以一个 \(\cos{mx}\) 使得整个式子更普遍。

\[\begin{align*} \int_{-\pi}^{\pi}f(x)\cos{mx}\space dx &= \int_{-\pi}^{\pi} a_0\cos{mx} dx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty} a_n\cos{mx}\cos{nx}dx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty} b_n\sin{nx}\cos{mx}dx \\ &=\int_{-\pi}^{\pi}a_n\cos^2{nx}dx + 0 +0 \\ &= \int_{-\pi}^{\pi}a_n\frac{1}{2}(1-cos2x)dx \\ &= \frac{1}{2}a_n(x - \frac{1}{2}\cos{2x})|^{\pi}_{-\pi} = \pi a_n \\ &\rightarrow a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos{nx}\space dx \tag{2.2.1} \end{align*} \]

2.3 Step3: :找\(b_n\)

\(b_n\) 的求法和 \(a_n\) 的求法相同，在等式两边乘上 \(\sin{mx}\) 再求积分，最后我们可以得到 \(b_n\)：

\[b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin{nx}\space dx \tag{2.3.1} \]

至此，证明完毕。

3.周期为\(2L\)的傅里叶级数展开

3.1利用换元求得一般傅里叶级数

周期为 \(2\pi\) 的周期函数 : \(f(x) = f(x+2\pi)\) ，同理周期为 \(2L\)的周期函数 ： \(f(t) = f(t+2L)\)

原理同周期为\(2\pi\)的傅里叶级数展开相同，但是我们只需要做一个简单的换元即可求得。我们知道一个周期函数是恒定的，有 \(\frac{x}{2\pi} = \frac{t}{2L}\) 。则有 ：\(x=\frac{\pi}{L}t\)

我们假设 \(g(x)\) 为周期为 \(2\pi\) 的函数，则\(g(x)\) 可以用傅里叶级数展开 :

\[g(x) = a_0 + \sum_{n=1}^{\infty}(a_n\cos{nx}+b_n\sin{nx}) \\a_0 = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx \quad\quad a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos{nx}dx \quad\quad b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin{nx}dx \tag{3.1.1} \]

我们将 \(x=\frac{\pi}{L}t\) 带入到 \(g(x)\) 当中 ：

①$x = \pi时\quad t = L $

②\(\int_{-\pi}^{\pi}dx\rightarrow\frac{\pi}{L}\int_{-L}^{L}dt\)

③$g(\frac{\pi}{L}t) =f(t)= a_0 + \sum_{n=1}^{\infty}(a_n\cos{\frac{n\pi}{L}t}+b_n\sin{\frac{n\pi}{L}t}) $

\[f(t) = a_0 + \sum_{n=1}^{\infty}(a_n\cos{\frac{n\pi}{L}t}+b_n\sin{\frac{n\pi}{L}t}) \\a_0 = \frac{1}{2L}\int_{-L}^{L}f(t)dt \quad\quad a_n = \frac{1}{L}\int_{-L}^{L}f(t)\cos{\frac{n\pi}{L}t}dt \quad\quad b_n = \frac{1}{L}\int_{-L}^{L}f(t)\sin{\frac{n\pi}{L}t}dt \tag{3.1.2} \]

3.2将傅里叶级数一般化

时域的表示，时域的横轴是时间，时间无负数 \(t>0\) 。则\(T = 2L\) 我们记 \(\omega = \frac{2\pi}{2L} = \frac{2\pi}{T}\) ，则傅里叶级数可以写成如下形式：

①\(\int_{-L}^{L} dt= \int_{0}^{2L} dt= \int_{0}^{T}dt\)

\[f(t) = a_0 + \sum_{n=1}^{\infty}(a_n\cos{n\omega t}+b_n\sin{n\omega t}) \\a_0 = \frac{1}{T}\int_{0}^{T}f(t)dt \quad\quad a_n = \frac{2}{T}\int_{0}^{T}f(t)\cos{n\omega t}dt \quad\quad b_n = \frac{2}{T}\int_{0}^{T}f(t)\sin{n\omega t}dt \tag{3.2.3} \]

至此我们已经完成了傅里叶的最基础的求解。但是我们觉得这个公式表达太过于繁杂，在实数域将这个公式简化有点苦难，所以我们引入复数将傅里叶级数公式进一步简化。

4.傅里叶级数的复数展开

4.1欧拉公式证明

我们知道欧拉公式为：\(e^{i\theta} = \cos\theta +i\sin\theta\)

如果我们要证明这个公式相等，我们可以令 ：\(f(x) = \frac{e^{i\theta}}{\cos\theta + i\sin\theta}\)

我们对 \(f(x)\) 求导 \(f'(x) = \frac{ie^{i\theta}(\cos\theta+i\sin\theta)-e^{i\theta}(-\sin\theta + \cos\theta)}{(\cos\theta + i\sin\theta)^2} = \frac{ie^{i\theta}(\cos\theta - \cos\theta)+e^{i\theta}(i\sin\theta-i\sin\theta)}{(\cos\theta + i\sin\theta)^2} = 0\)

导数\(f'(x) = 0\) 说明 \(f(x)\) 是一个常数，我们随便带入一个数来求 \(f(x)\) : \(f(x) = f(0) = \frac{e^0}{\cos0} = \frac{1}{1} = 1\)

说明欧拉公式 \(e^{i\theta} = \cos\theta +i\sin\theta\) 成立。

4.2cos、sin复数表示

由欧拉公式的证明可知：不论在什么条件下 ①\(e^{i\theta} = \cos\theta +i\sin\theta\) 均成立。

我们将 \(-\theta\) 带入到欧拉公式当中 : ②\(e^{-i\theta} = \cos(-\theta) +i\sin(-\theta) = \cos\theta-i\sin\theta\)

将欧拉公式和上述的 ①和②公式进行联立，可以得到：

\[\cos\theta = \frac{1}{2}(e^{i\theta}+e^{-i\theta}) \\ \sin\theta = -\frac{i}{2}(e^{i\theta}-e^{-i\theta}) \\ \tag{4.2.1} \]

4.3复数形式展开

我们已知傅里叶级数的一般化为：

\[f(t) = \frac{1}{2}a_0 + \sum_{n=1}^{\infty}(a_n\cos{n\omega t}+b_n\sin{n\omega t}) \\a_0 = \frac{2}{T}\int_{0}^{T}f(t)dt \quad\quad a_n = \frac{2}{T}\int_{0}^{T}f(t)\cos{n\omega t}dt \quad\quad b_n = \frac{2}{T}\int_{0}^{T}f(t)\sin{n\omega t}dt \tag{3.2.3} \]

具体的推导过程：

\[\begin{align*} f(x) &= \frac{1}{2}a_0 + \sum_{n=1}^{\infty}(a_n\cos{n\omega t}+b_n\sin{n\omega t}) \\ &= \frac{1}{2}a_0 + \sum_{n=1}^{\infty}[\frac{1}{2}a_n(e^{in\omega t}+e^{-in\omega t}) -\frac{i}{2}b_n(e^{in\omega t}-e^{-in\omega t})] \\ &= \frac{1}{2}a_0 + \frac{1}{2}\sum_{n=1}^{\infty}[e^{in\omega t}(a_n - ib_n)+e^{-in\omega t}(a_n + ib_n)]\\ &= \sum_{n=0}^{0}\frac{1}{2}a_0·e^{in\omega t}+ \sum_{n=1}^{\infty}\frac{1}{2}e^{in\omega t}·(a_n - ib_n) + \sum_{-\infty}^{n=-1}\frac{1}{2}e^{in\omega t}(a_{-n}+b_{-n}) \\ &= \sum_{-\infty}^{\infty}C_ne^{in\omega t} \tag{4.3.1} \end{align*} \]

具体的公式已经推导完成，接下来就是讨论\(C_n\) 的情况，\(C_n\) 的情况有三种 \(C_n=\left\{ \begin{aligned} n & =0 & \frac{1}{2}a_0 \\ n & >0 & \frac{1}{2}(a_n - ib_n) \\ n & <0 & \frac{1}{2}(a_{-n} + ib_{-n}) \end{aligned} \right.\)

①n=0

\[C_n = \frac{1}{2}a_0 = \frac{1}{T}\int_{0}^{T}f(t)dt = \frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t}dt \tag{4.3.2} \]

②n>0

\[\begin{align*} C_n&=\frac{1}{2}(a_n - ib_n) = \frac{1}{2}(\frac{2}{T}\int_{0}^{T}f(t)\cos{n\omega t}dt - \frac{2}{T}\int_{0}^{T}f(t)\sin{n\omega t}dt) \\ &= \frac{1}{T}\int_{0}^{T}f(t)(\cos{n\omega t}-i\sin{n\omega t})dt \\ &=\frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t}dt \tag{4.3.3} \end{align*} \]

②n<0

\[\begin{align*} C_n&=\frac{1}{2}(a_{-n} + ib_{-n}) = \frac{1}{2}[\frac{2}{T}\int_{0}^{T}f(t)\cos{(-n)\omega t}dt + \frac{2}{T}\int_{0}^{T}f(t)\sin{(-n)\omega t}dt] \\ &=\frac{1}{T}\int_{0}^{T}f(t)(\cos{n\omega t}-i\sin{n\omega t})dt \\ &=\frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t}dt \tag{4.3.4} \end{align*} \]

综上：\(f(x) = \sum_{-\infty}^{\infty}C_ne^{in\omega t}\) ，\(C_n = \frac{1}{T} \int^{T}_{0}f(t)e^{-in\omega t}\)

5.傅里叶变换 Fourier Transform

傅里叶级数解决的是周期函数的表达问题，其频谱图是离散的。傅里叶变换解决的是非周期函数的表达问题，其频谱图是连续的。我们上面已经使用一个统一的式子来表达傅里叶级数了，如何将傅里叶级数转换到傅里叶变换，是这一部分的重点内容。这需要一点高数的内容\((i)\) 黎曼和思想 \((ii)\) 频谱图

5.1连续傅里叶变换

假设对于一个周期性的函数 \(f(x) = \sum_{-\infty}^{\infty}C_ne^{in\omega t}\) , \(C_n = \frac{1}{T} \int^{T}_{0}f(t)e^{-in\omega t}\) ，其函数图像如下： （左：时域图 右：频域图）

我们记\(\omega_0 = \frac{2\pi}{T}\) 记为基频率。

如果我们使用频谱图将傅里叶级数表示出来： \(①f(x) = \dots C_{-1}e^{-i\omega t}+C_{0}e^{0}+C_{1}e^{i\omega t}+C_{2}e^{2i\omega t}+\dots\)

而\(C_n\) 是一个复数，我们可以统一地将其写成： \(②a+bi\)

通过\(①\)和\(②\)便可以画出三维的频谱图像，可以想象得到这个图像是离散的。傅里叶级数我们可以理解成为离散的傅里叶变换。下面是

我们由黎曼和的思想，当周期无限大的时候 \(T\rightarrow \infty\) ，\(\omega_o = \frac{2\pi}{T} \rightarrow 0^+\)上述频谱图的 \(\textcolor{red}{n\omega_0}\) 轴的 \(\omega_0\) 趋于 \(0\) 的时候，频谱图将慢慢变得连续，最终变成一条连续的三维空间的曲线。

对于非周期函数，有：

\(①T\rightarrow \infty\) \(\rightarrow\) \(\lim_{T->\infty}f_T(t) = f(t)\)

\(②\Delta\omega = (n+1)\omega_0 - n\omega_0 = \omega_0\)

\(③\Delta\omega = \omega_0 =\frac{2\pi}{T}\) \(\rightarrow\) \(\frac{1}{T} = \frac{\Delta\omega}{2\pi}\) \(\rightarrow\) \(\lim_{T->\infty} \Delta\omega \rightarrow 0^{+}\)

\(④\sum_{n=-\infty}^{\infty} n\omega_0 =\sum_{n=-\infty}^{\infty} n\Delta\omega = \int_{-\infty}^{\infty} d\omega\)

然后我们将 \(\Delta\omega\) 和 \(C_n\) 带入到周期函数 \(f_T(t)\) 中：

\[\begin{align*} f_T(t) &= \sum_{-\infty}^{\infty}C_ne^{in\omega t} \\ &= \sum_{-\infty}^{\infty}\frac{1}{T} \int^{\frac T 2}_{-\frac T 2}f_T(t)e^{-in\omega_0 t}dt \space e^{in\omega_0 t} \\ &= \sum_{-\infty}^{\infty} \frac{\Delta\omega}{2\pi} \int^{\frac T 2}_{-\frac T 2}f_T(t)e^{-in\omega_0 t}dt \space e^{in\omega_0 t} \tag{5.1.1} \end{align*} \]

当\(T\rightarrow \infty\) 的时候，我们利用上述已经写好的 \(①②③④\)条件：

\[\begin{align*} \lim_{T\rightarrow\infty} f_T(t) &= f(t) \\ &=\frac {1}{2\pi}\int_{-\infty}^{\infty} \int^{\frac T 2}_{-\frac T 2}f(t)e^{-i\omega t}dt \space e^{i\omega t} d\omega \\ &=\frac {1}{2\pi}\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt \space e^{i\omega t} d\omega \tag{5.1.2} \end{align*} \]

则傅里叶变换（时域到频域）应该为：

\[F(\omega) = \int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt \tag{5.1.3} \]

而逆傅里叶变换（频域到时域）则为：

\[f(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega \tag{5.1.4} \]

5.2 傅里叶变换的理解

5.2.1 Pre Knowledge : Time Domain And Frequency Domain

时域：以时间作为参考来观察动态世界世界的方法，称为时域分析。

频域：如果时域分析是以时间为轴，那么世间万物都是出于改变的状态。如果存在另一种方式来观察世界，并且这个世界是一成不变的话，你会不会觉得我已经疯掉了，这个方式就是频域分析。

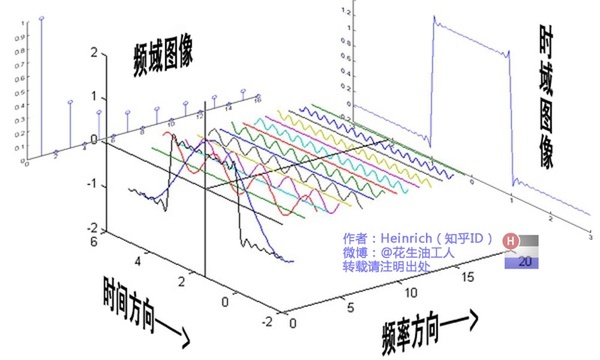
频谱图：我们刚刚求的的公式 \(\text{5.1.2} \quad \lim_{T\rightarrow\infty} f_T(t) = \frac {1}{2\pi}\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt \space e^{i\omega t} d\omega \tag{5.1.2}\) 就是一个对于时间频率的三维的频谱图。

• 🖲️ 傅里叶变换：从时域或空域（原始信号）转到频域，它通过分解信号成正弦或余弦波,以频率和幅度来表达信号。 时域 → 频域

• 🖲️ 傅里叶逆变换：从频域转换回到时域或者空域，它可以通过频域表达或者重构出原始信号。 频域 → 时域

我们现在在回来查看傅里叶变换和傅里叶逆变换，所谓频域就是消除时间的影响，而时域就是消除频率的影响。傅里叶变换从时域变成频域，也就是要对上面的重积分对定义域内的时间做积分： \(F(\omega) =\int_{t=-\infty}^{t=+\infty}\lim_{T\rightarrow\infty} f_T(t)~dt = \int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt \quad \text{From 5.1.3}\)

而傅里叶逆变换，则是对定义域内的频率做积分，傅里叶逆变换是在进行了傅里叶变换之后才能够进行的操作：\(\int_{\omega=-\infty}^{\omega=+\infty} \lim_{T\rightarrow{\infty}}{f_T(t)}~d\omega = \frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega \quad \text{From 5.1.4}\)

如果上图频谱图从侧面进行观察，我们将得到频域图或者时域图，如果我们往下观察会得到什么呢？相位谱。 为什么要提到相位谱，因为不管是频域图还是时域图，都是存在信息缺失的。不同的相位决定了波的位置，所以对于频域分析，仅仅有频谱是不够的。

5.2.2 相位谱（phase spectrum）

在进行从下面往下看之前先了解如下公式，这个公式叫做基础正弦波公式：

\[f(t) = A\sin{(\omega{t} + \varphi )} \tag{One Standard Signal} \]

上述 \(A\) 表示振幅，\(\omega\) 表示角频率，\(\varphi\) 为初相，\(t\) 表示时间，\(f(t)\) 表示动点的位置。

1. 频率(Frequency): \(\color{brown} \omega\)
   • 频率表示信号震荡的快慢。频率越高，信号的变换越快；频率越低，信号的变化就越慢。 在傅里叶变换中我们可以得到信号在不同频率 \(\omega\) 上的频域表达 \(F(\omega)\) ，这些频率的成分就构成了原始信号。通过频率，我们判断信号中哪些速率的频率占据主导。在图形中，低频表示图像平滑变化，高频表示图像细节与边缘。频率的单位是 赫兹\(\text{(Hz)}\) 。
   • 简而言之：频率表示信号的快慢，决定信号中的代表什么样的变化特征。
2. 幅度(Amplitude)：\(\color{brown} A\)
   • 幅度表示信号成分大小或强度。在傅里叶变换中成分\(F(\omega)\)的大小就是幅度。幅度决定了该频率成分在重构原信号中的贡献程度。幅度较大表示该频率在信号中占有较大权重。幅度的单位是 毫米\(\text{(mm)}\)。
   • 简而言之：幅度表示信号强度,决定该频率成分的重要性。
3. 相位(Phase)：\(\color{brown} \omega{t}+\varphi\)
   • 相位表示信号的位置或状态,以度数或弧度为单位测量。它决定了信号成分的正弦或余弦形式。相位不同会导致信号的位置、振幅及波形都发生改变。单位是弧度制 \(\text{rad}\) 。

单位的转换：\(①1\text{Hz} = 1\text{s}^{-1}\Rightarrow frequency=\frac{1}{T} = \frac{1}{s} = 2\pi{f} \quad ②\omega = \frac{2\pi}{T} = 2\pi{f} \Rightarrow \text{rad/s}\)

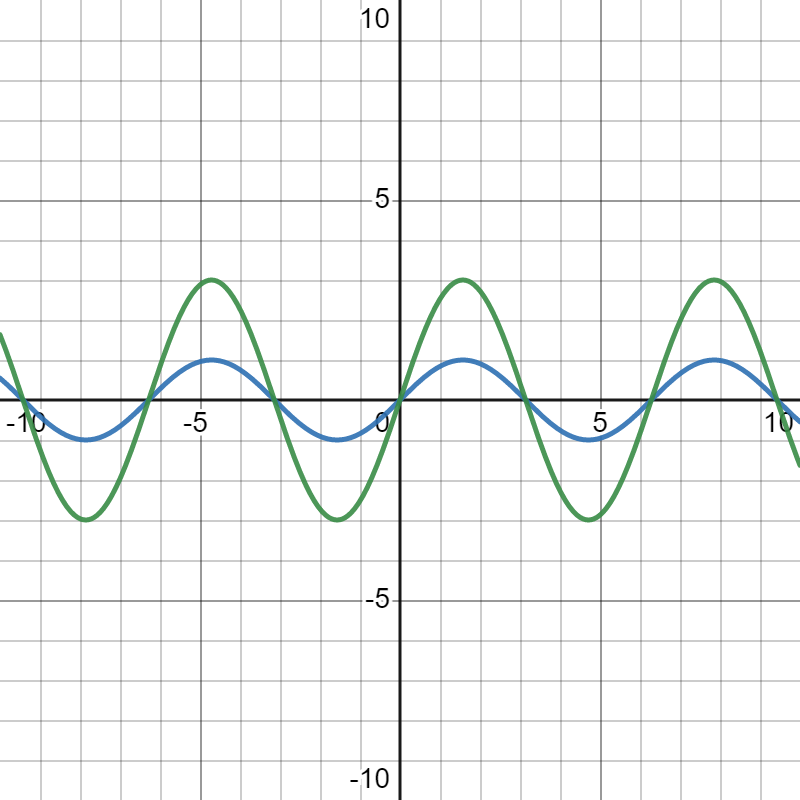
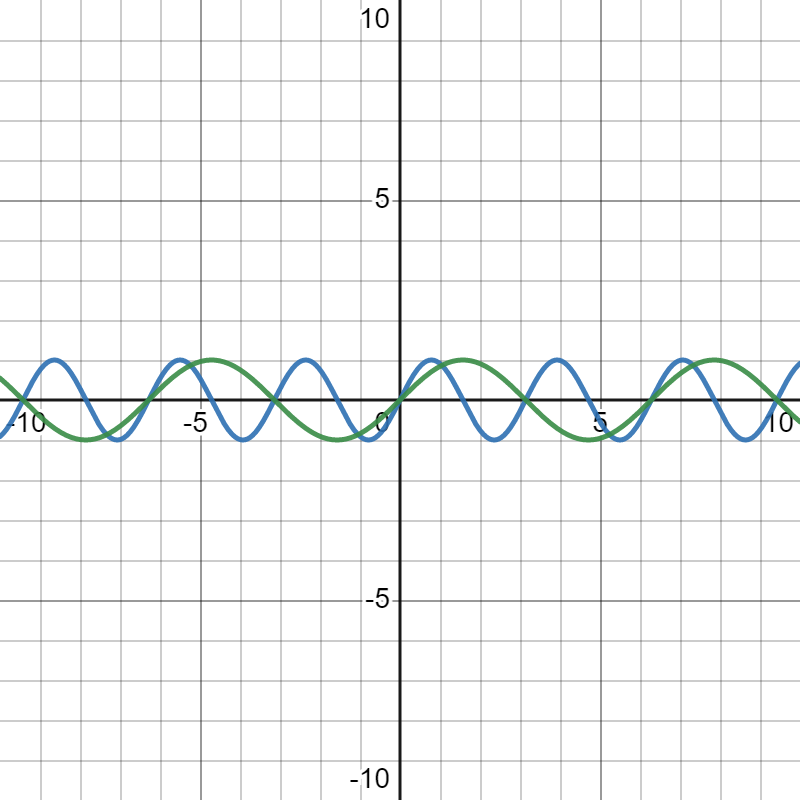
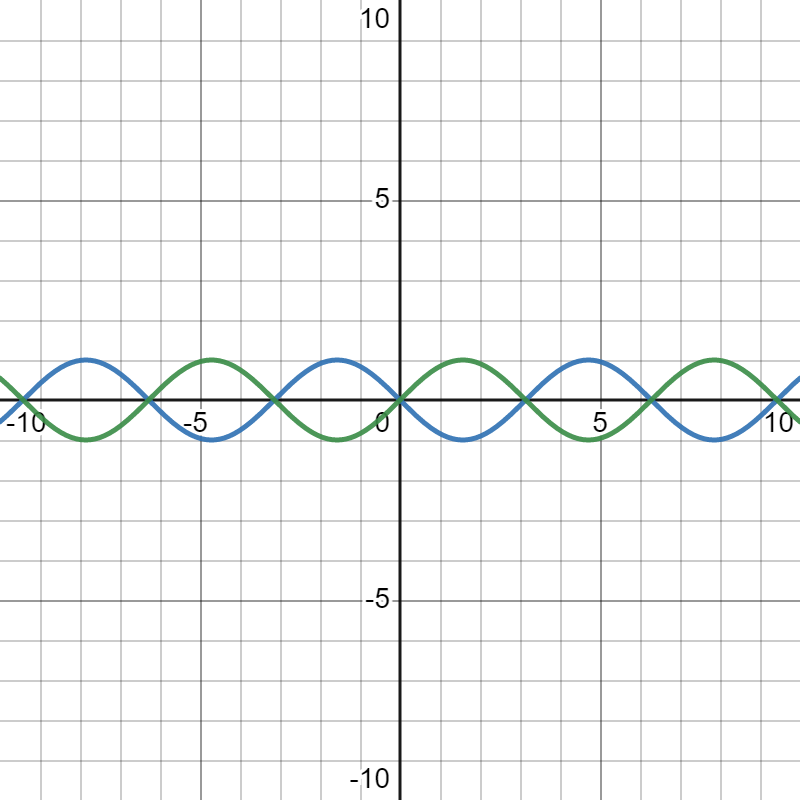
上面的\(\text{1,2,3}\) 引用了GPT的回答，简单来说就是，幅度控制了振幅强度（左一 ：\(\color{blue}\sin{x},\color{green}3\sin{x}\) 区别），频率控制了波的形状（中间：\(\color{blue}\sin{x},\color{green}\sin{2x}\)）,而相位控制了图像的位移（右一：\(\color{blue}\sin{(x+\pi)},\color{green}\sin{(x)}\)）

----------

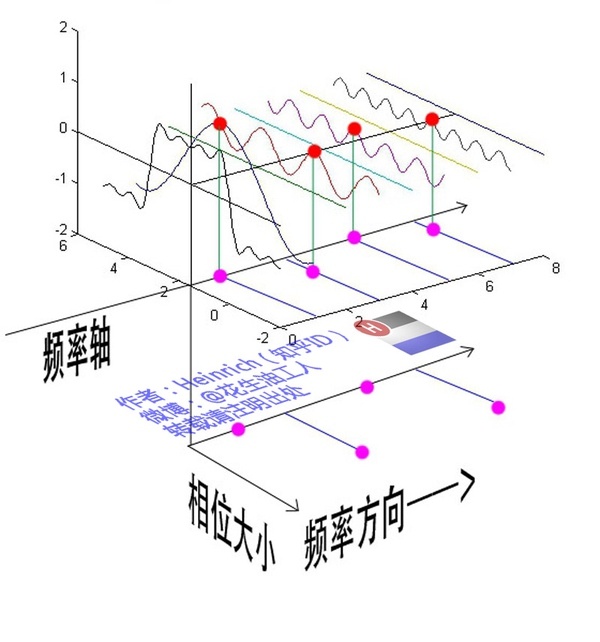
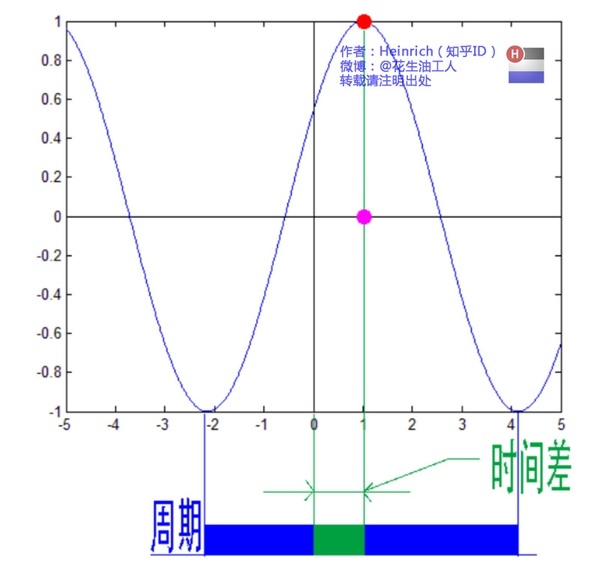
下面继续来说相位谱，下面的图是由七个不同的正弦波叠加构成。相位我们刚刚也说了，表示的是波的状态或者位置，鉴于正弦波是周期性的，我们需要设定一个用来标记正弦波位置的东西。在图中就是小红点，小红点是距离频率轴 \(\omega_i = 0\) 最近的波峰。 这些粉色的点只标注了波峰距离频率轴的距离，并不是相位。时间差 \(≠\) 相位差，要得到相位还需要乘以 \(\frac{2\pi}{T}\) ，如果将一个周期看成是 \(2\pi\) 或者 \(360°\)的话，相位差就是在一个周期内占的比重。

5.2.3 你曾经看过大海吗？关于傅里叶变换的直观理解

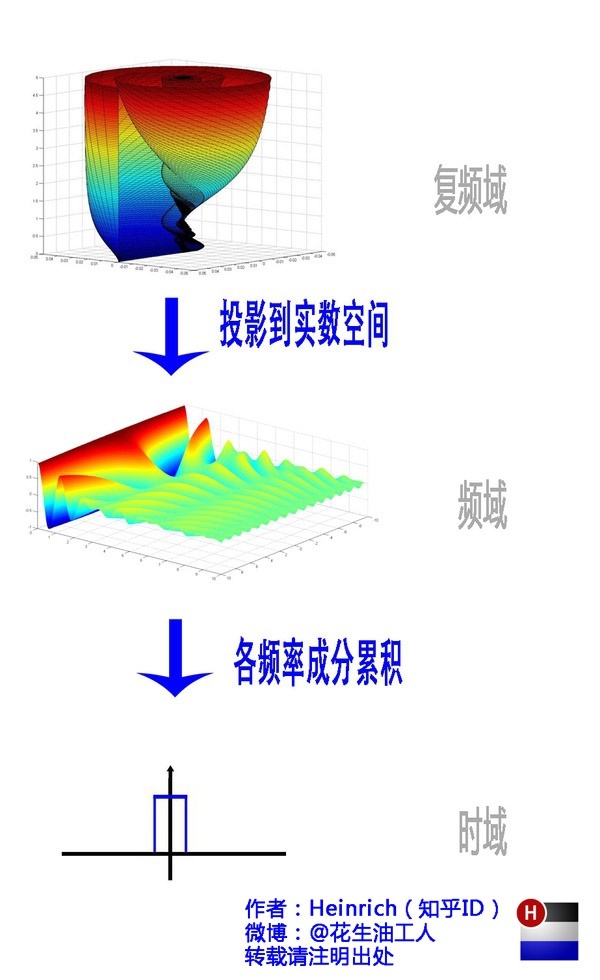
刚才都只是谈论离散的频谱图，我们推出来的公式不是连续的吗？那么连续的频谱图应该张成什么样子呢？

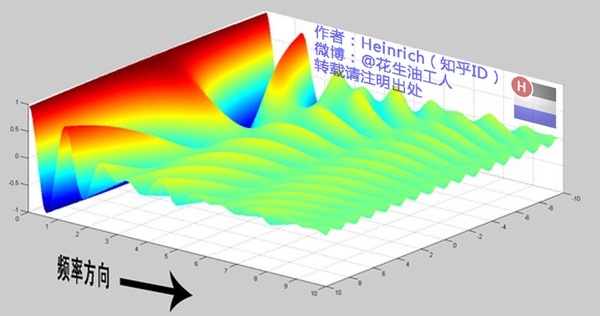
有没有想象出来，就像大海一样。原来离散谱的叠加，变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号，也就是 \(\text{5.1.1}\) 的公式的由来。

接下来就是吹嘘时间，我们上面有证明过欧拉公式 \(e^{i\theta} = \cos\theta +i\sin\theta \quad \text{(Chapter 4.1)}\) 的正确性。但是谁知道这个优美的公式长成什么样子吗？

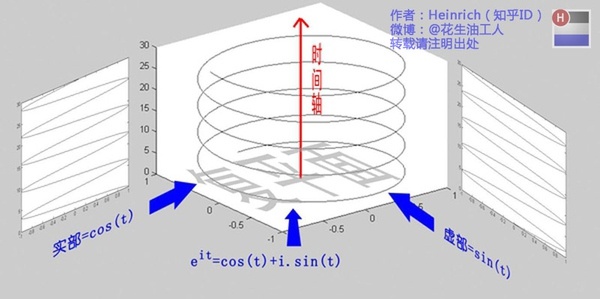
欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。如果只看它的实数部分，也就是螺旋线在左侧的投影，就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。

刚刚我们看过了频谱图的“大海”，却未曾见过复数域下的欧拉公式的“大海”。这个换算回实数域就是频谱图的大海。而其时域就是右边的图。

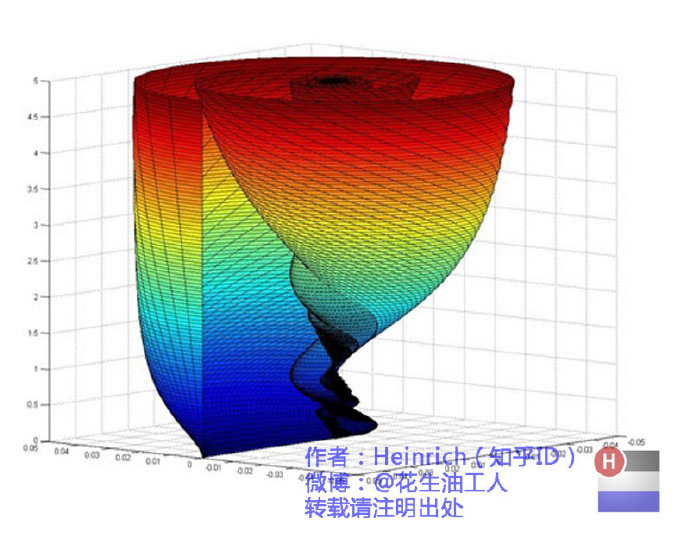<--复频域，时域--->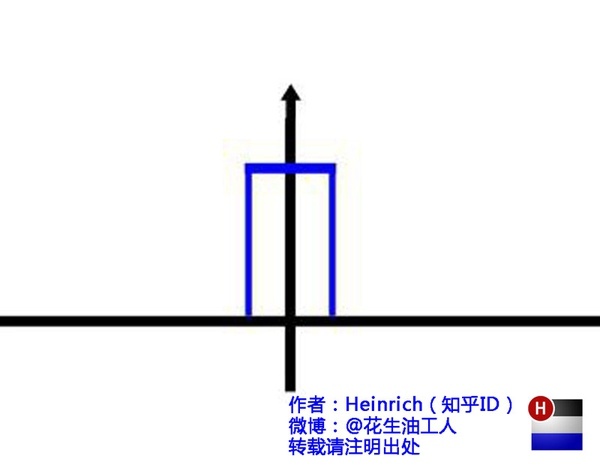

所以我们可以得出傅里叶变换的最终结论：

5.2.3 二维图像和频谱图的关系

上图是一个从灰度图通过傅里叶变换得到一个频域图，时域\(\rightarrow\) 频域的转换。其中中心最亮的点是频率最低点，往四面八方逐渐变成高频，并且左上-右下是完全对称。其中黑色部分即表明该图像不含有该部分的频率，相反颜色越亮，代表该频率的幅值越高。通常我们会发现中心处是最亮的，即低频信号是最多的，这也和原时域图的信息是匹配的。

关于频谱图，通常其大小是和原图像一样，但是其\((u,v)\) 坐标却与原图的\((u,v)\) 坐标没有一一对应的关系。

5.3 傅里叶变换的性质

傅里叶变换有很多种性质：如【线性】，【奇偶性】，【对称性】，【尺度变换】，【时移延迟特性】，【卷积】，【时域微分，积分】，【频域积分，微分】等等 ，我们主要研究其 ①奇偶性 ②卷积 ③ 时域微分，积分 ④ 频域积分，微分

前提：

\(①\)傅里叶相关：

傅里叶变换公式 ：$ F(\omega) = \int_{t=-\infty}^{t=+\infty} f(t)e^{-i\omega{t}}~dt$

逆傅里叶变换公式： \(f(t) = (\int_{\omega = -\infty}^{\omega = +\infty} F(\omega)e^{i\omega{t}}~d\omega)/2\pi\)

\(f(t)\) 称为\(F(\omega)\) 的傅里叶变换或者说原函数，并且： \(\int_{t=-\infty}^{t=+\infty}|f(t)|~dt < \infty\)

\(②\)阶跃函数：

阶跃函数又称奇异函数，在不同的领域中有不同的说法，公式长这样（我也不想去解释那个又臭又长有无聊的定义╮(╯▽╰)╭）：

\[\begin{flalign} \varepsilon{(t)} = \begin{cases} 0\quad,\quad t<0 \\ 1/2 ,\quad t = 0 \\ 1\quad ,\quad t>0\end{cases} \qquad \&\& \qquad \int_{t=-\infty}^{t=+\infty}\varepsilon{(t)}\varphi(t)~\mathrm dt = \int_{0}^{+\infty}\varphi{(t)}~\mathrm d t \tag{Step Function Expression} \end{flalign} \]

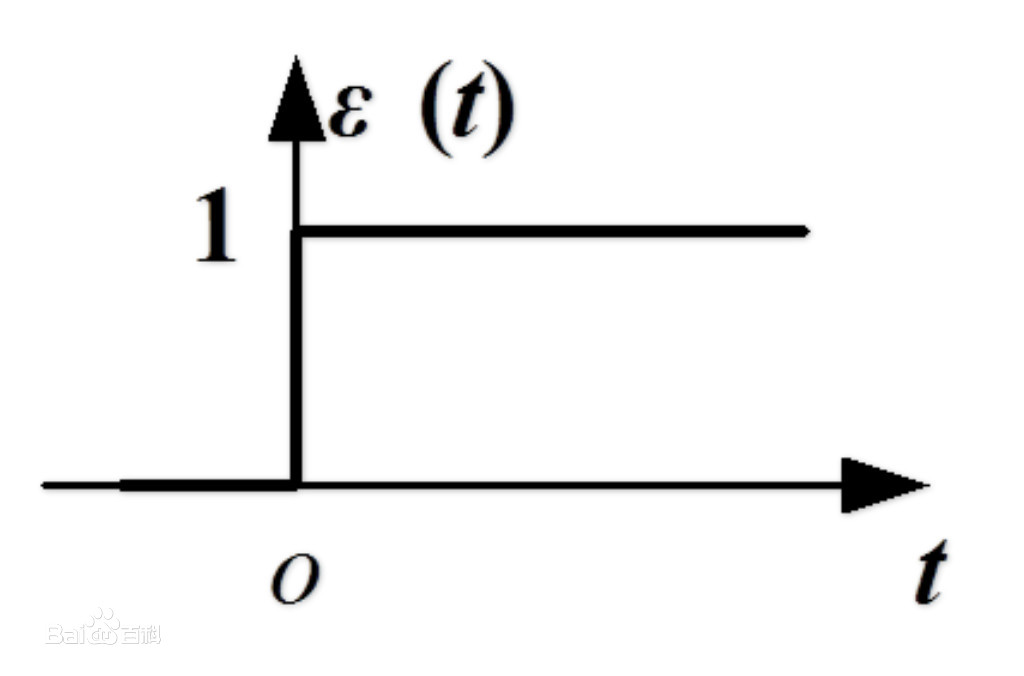--->就长这样：---->积分之后长这样：

\(③\)冲击函数：

单位冲击函数和阶跃函数长得很像但是又刚好长得相反，公式长这样：

\[\begin{flalign} \delta(t) = \begin{cases} \infty \quad t = 0 \\ ~0 \quad ~t≠0 \end{cases} \qquad \&\& \qquad \int_{t=-\infty}^{t=+\infty}\delta{(t)}~dt=1 \tag{Impulse Function Expression} \end{flalign} \]

冲击函数和阶跃函数的关系：

\((i)\)单位冲击函数等于单位阶跃函数对时间变量的导数：\(\delta{(t)} = \frac{\mathrm {d}\varepsilon{(t)}}{\mathrm t}\)

\((ii)\)单位阶跃函数等于单位冲击函数的积分：\(\varepsilon{(t)} = \int_{0}^{t} \delta{(s)} ~\mathrm d s\)

**③常用傅里叶变换对： **

\(\text{(i)}\)单边指数函数: $f(t) = e^{-\alpha{t}}\varepsilon(t)\quad \quad \alpha > 0 \quad & \quad t≥0 $

采用解析法求单边指数信号的傅里叶变换，将单边指数信号乘以 exp(-iwt) 在定义域 t 进行积分。

\[\begin{flalign}\left. F(\omega) = \int_{-\infty}^{\infty} e^{-at} e^{-i\omega{t}} \varepsilon{(t)} ~ \mathrm dt = \int_{0}^{\infty} e^{-at} e^{-i\omega{t}} \mathrm dt = \int_{0}^{\infty} e^{-t(a+i\omega{t})} ~\mathrm dt = \frac{e^{-t(a+i\omega)}}{-(a+i\omega )} \right|^{+\infty}_{0} = \frac{1}{(a+i\omega )} \tag{5.3.1} \end{flalign} \]

我们可以得到 1. 幅度：\(|F(\omega)| = \frac{1}{\sqrt{\alpha^2+\omega^2}}\) 2. \(\varphi(\omega) = \arctan{(\frac{-\omega}{a})} = -\arctan{(\frac{\omega}{\alpha})}\)

a=1时候计算得到的频域谱和相位谱

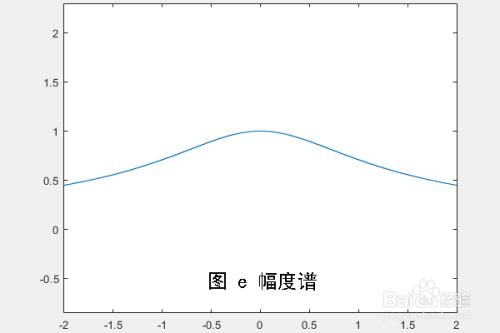
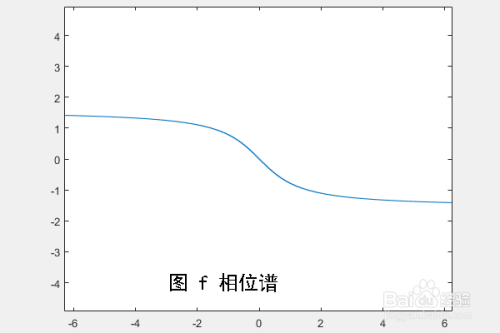
\(\text{(ii)}\)双边指数函数： \(f(t) = e^{-\alpha{|t|}}\varepsilon(t)\quad ,~ \alpha > 0 \quad \& \quad t\in{R}\)

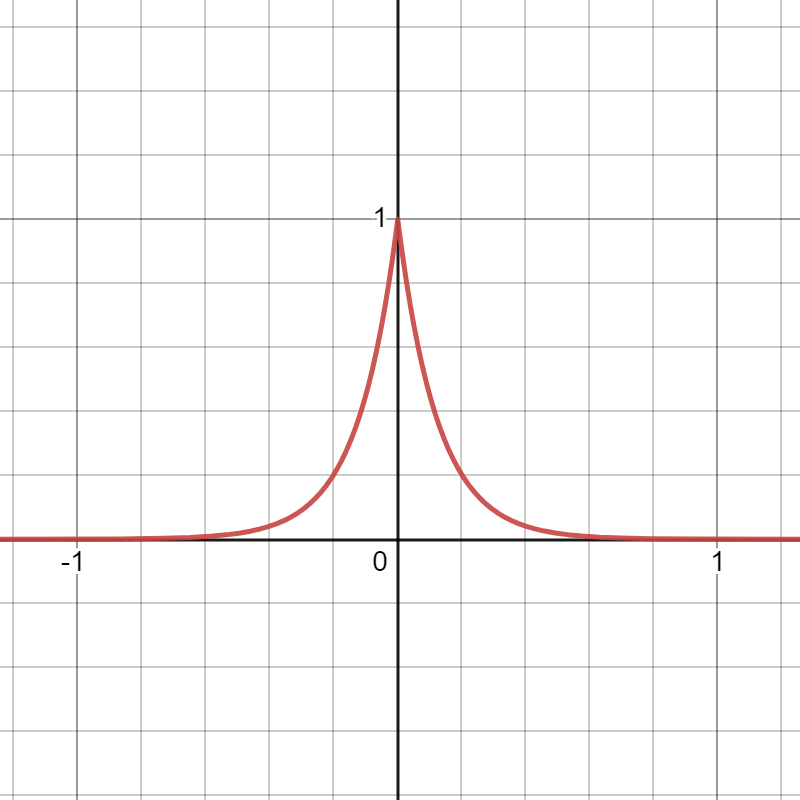和求解单边指数函数一样，都是采用解析法求解，需乘上 exp(-iwt) 在定义域 t 进行积分。

\[\begin{flalign} F(\omega) &= \int_{t=-\infty}^{t=0} e^{\alpha{t}} e^{-i\omega{t}} \mathrm dt + \int_{t=0}^{t=+\infty} e^{-\alpha{t}} e^{-i\omega{t}} \mathrm dt = \left.\frac{e^{(\alpha-i\omega)t }}{\alpha-i\omega} \right|^{0}_{-\infty} + \left. \frac{e^{-(\alpha+i\omega)t }}{-(\alpha+i\omega)}\right|_{0}^{+\infty} = \frac{1}{\alpha-i\omega} +\frac{1}{\alpha+i\omega} \\ &=\frac{2\alpha}{\alpha^2 + \omega^2} \tag{5.3.2} \end{flalign} \]

上面直接省略去了 \(\varepsilon{(t)}\) ，直接省略的原因是双边指数是一个偶函数，左边等于右边，所以左边的式子可以写成：

\[\begin{flalign} \int_{t=-\infty}^{t=0} e^{\alpha{t}} e^{-i\omega{t}} \varepsilon{(t)}~\mathrm dt = \int_{t=0}^{t=+\infty} e^{-\alpha{t}} e^{i\omega{t}} \varepsilon{(t)}~\mathrm dt = \int_{t=0}^{t=+\infty} e^{-\alpha{t}} e^{i\omega{t}} ~\mathrm dt = \int_{t=-\infty}^{t=0} e^{\alpha{t}} e^{-i\omega{t}} ~\mathrm dt \end{flalign} \]

右边同理：\(\int_{t=0}^{t=+\infty} e^{-\alpha{t}} e^{-i\omega{t}} \mathrm dt\)

\(\text{(iii)}\)门函数 - 矩形脉冲： \(\text{rect}(t) = \begin{cases} E\quad ,|t|≤ \frac T2 \\ 0\quad ,|t|> \frac T2\end{cases}\)

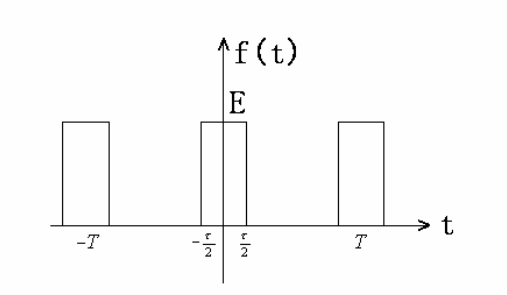
上面的公式可能不能够很好理解门函数，我们来具体了解一下：

1. 矩形脉冲是一种周期函数，每个 \(T\) 时间内，它有一个宽度为 \(T\) 的方波脉冲。
2. 单个脉冲信号积分值为 \(T\) ：\(\int_{t=-\tau}^{t=+\tau} \text{rect}(t) \mathrm dt = 2E\tau = TE\)
3. 当 \(T\rightarrow+\infty\) 时，上图中仅有 \((-\tau ,\tau)\) 存在 \(f(t) = E\)，此时傅里叶变换的结果应是连续的。

\[\begin{flalign} F(\omega) &=\int_{t = -\infty}^{t = +\infty} f(t) e^{-i\omega{t}} \mathrm dt = \int_{t=-\frac\tau 2}^{t=\frac\tau 2} \text{rect}(t) e^{-i\omega{t}} \mathrm dt = \left. \int_{t=-\frac\tau 2}^{t=\frac\tau 2} E e^{-i\omega{t}} \mathrm dt = \frac E{-i\omega} e^{-i\omega{t}} \right|^{\frac\tau 2}_{-\frac\tau 2} \\ &=\frac E{-i\omega}(e^{-i\omega{\frac\tau 2 }} - e^{i\omega{\frac\tau 2}}) \tag{5.3.3} \end{flalign} \]

上面的结果看起来不太美观，我们通过 ChatGPT 得知 \(\text{sinc}\) 函数和指数函数 \(\text{e}\) 存在线性组合关系，\(\Rightarrow\text{sinc}(x) = \sin{(x)}/x = (e^{ix} - e^{-ix}) / 2ix\)

FROM  CHAT  GPT : 

\(\text{sinc}\) 函数定义为：\(\text{sinc}(x) = \sin{x}/x\)

\(\sin{x}\) 和欧拉公式的关系： $\begin{cases} e^{ix} = i\sin{x} + \cos{x} \ e^{-ix} = -i\sin{x} + \cos x \end{cases} \Rightarrow $ \(e^{ix} - e^{-ix} = 2i\sin{x} \Rightarrow\) \((e^{ix} - e^{-ix})/2i = \sin{x}\)

\(\text{sinc}\) 和 \(e\) 的关系可以用欧拉公式表示：

\[\text{sinc}(x)=(e^{ix}-e^{-ix})/2i = ((i\sin{x}+\cos{x}) - (\cos{x}-i\sin{x}))/2xi = 2i\sin{x}/2xi = \sin{x}/x \]

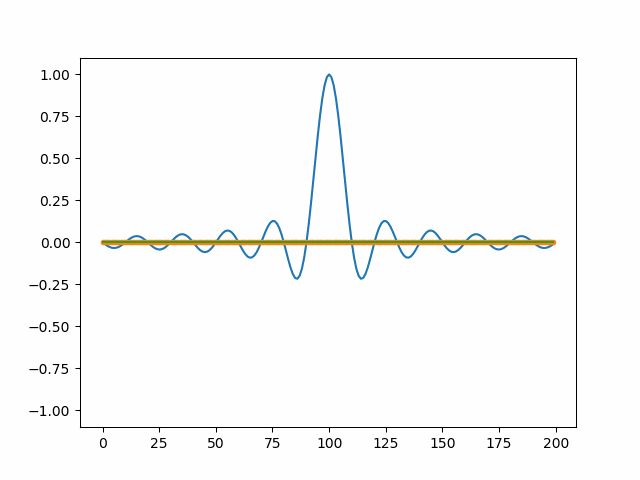
所以一个周期为 \(\tau\) 的矩形脉冲的傅里叶变换可以写成 ：\(F(\omega) = \int_{-\frac{\tau}{2}}^{\frac{\tau}{2}} E e^{-i\omega t} dt = E\tau \text{sinc}\left(\frac{\omega\tau}{2}\right)\)

具体的推到如下：

\[\begin{flalign} F(\omega) &= \int_{t=-\infty}^{t=+\infty} f(t) e^{-i\omega{t}} \mathrm dt = E\int_{t=-\frac\tau2}^{t=\frac\tau2} e^{-i\omega{t}} \mathrm dt \\ &=\frac E{-i\omega}(e^{-i\omega{\frac\tau 2 }} - e^{i\omega{\frac\tau 2}}) \\ &=\frac {2E}{\omega} (\frac{e^{i\omega{\frac\tau 2 }}- e^{-i\omega{\frac\tau 2}}}{2i}) \\ &=\frac {2E}{\omega}\sin{(\frac{\omega\tau}{2})} \\ &=E\tau \frac{\sin{(\frac{\omega\tau}{2})}}{\frac{\omega\tau}{2}} \\ &=E\tau \text{sinc}(\frac{\omega{t}}{2}) \# \end{flalign} \]

矩形脉冲傅里叶变换后的图像→→

5.3.1 傅里叶变换の奇偶性

奇偶性性质：

1. 如果原始信号 \(f(t)\) 是实数信号（即没有虚部） ，那么其傅里叶变换F(ω)具有共轭对称性，即\(F(-ω) = F^*(ω)\)，其中 \(^*\) 表示共轭。
2. 如果原始信号f(t)是偶函数（即\(f(-t) = f(t)\)），那么其傅里叶变换\(F(ω)\)也是偶函数，即\(F(-ω) = F(ω)\)。
3. 如果原始信号f(t)是奇函数（即\(f(-t) = -f(t)\)），那么其傅里叶变换F(ω)也是奇函数，即\(F(-ω) = -F(ω)\)。
4. 如果原始信号\(f(t)\)是实数偶函数，那么其傅里叶变换\(F(ω)\)是实数偶函数。
5. 如果原始信号\(f(t)\)是实数奇函数，那么其傅里叶变换\(F(ω)\)是虚数奇函数。

所以我们可以对原始信号 \(f(t)\) 分情况分析：\(①\)实函数 \(②\)实偶函数 \(③\)实奇函数。

由傅里叶变换：\(F(\omega) = \int_{-\infty}^{+\infty}f(t)e^{-i\omega{t}}\mathrm dt = \int_{-\infty}^{+\infty}f(t)\cos{\omega{t}}~\mathrm dt -i\int_{-\infty}^{+\infty}f(t)\sin{\omega{t}}~\mathrm dt\)

所以频谱可以分成两个部分：\(Re(\omega) = \int_{-\infty}^{+\infty}f(t)\cos{\omega{t}}~\mathrm dt\quad\) \(\quad Im(\omega) = -\int_{-\infty}^{+\infty}f(t)\sin{\omega{t}}\)

幅度：\(|f(t)| = \sqrt{R^2(\omega)+I^2(\omega)}\) 相位：\(\varphi{(\omega)} = \arctan{(\frac{I{(\omega)}}{R{(\omega)}})}\)

\(\text{(i)}\)原始信号是实函数

先解释一下什么是实函数：没有虚部的函数。

假设共轭傅里叶为 \(F^*(\omega)\) ，原傅里叶为 \(F(\omega)\)

5.4 傅里叶变换的应用

5.4.1 图像增强与图像去噪

绝大部分的噪音都是图像中的高频分量，通过设计低通滤波器来滤去高频。边缘也是图像的高频分量，可以通过添加高频分量来增强原始图像的边缘。下次新开文章说吧。

我是一名正在学习计算机图形学的学渣，希望我的文章能够帮助你，加油陌生人❤。

6.文章引用

1.第一期纯干货数学推导傅里叶级数与傅里叶变换Part1三角函数的正交性

2.第二期纯干货数学推导傅里叶级数与傅里叶变换Part2周期为2Pi的函数展开

3.第三期纯干货数学推导傅里叶级数与傅里叶变换Part3周期为2L的函数展开

4.第四期纯干货数学推导傅里叶级数与傅里叶变换Part4傅里叶级数的复数形式

5.第五期纯干货数学推导傅里叶级数与傅里叶变换Part5从傅里叶级数推导傅里叶变换

6.总结篇纯干货数学推导傅里叶级数与傅里叶变换Part6总结与闲话（完)

[7.计算机图形学（第二版） Fundamentals of Computer Graphics ([美] 舍利, Peter Shirley, 高晓春译) (Z-Library)](C:\Users\杨树森\Desktop\PDF WORKSHEET\计算机图形学（第二版） Fundamentals of Computer Graphics ([美] 舍利, Peter Shirley, 高晓春译) (Z-Library) (1).pdf)

8.深入浅出的讲解傅里叶变换（真正的通俗易懂）