Pytorch 4.6 Dropout 暂退法

Waht's Dropout ?

上一节 权重衰减：\(L2\) 正则化 通过介绍添加 \(L_2\) 正则化来减少过拟合的情况的出现。这一节我们使用Dropout Layer 来证明 \(L2\) 正则化的正确性。

• Dropout 的意思是每次训练的时候随机损失掉一些神经元， 这些神经元被Dropped-out了,换句话讲，这些神经元在正向传播时对下游的启动影响被忽略，反向传播时也不会更新权重。
• Dropout 的效果是，网络对某个神经元的权重变化更不敏感，增加泛化能力，减少过拟合。

How to add Dropout?

添加Dropout-Layer的过程就相当于再给我们的模型添加一些噪声，以此增加模型的平滑度，达到增强适应性的特点。
添加Dropout层的原则：

1. 添加噪声而不影响原本数据的固有特征，一种想法是以一种 无偏向（unbiased）的方式注入噪声。 这样在固定住其他层时，每一层的期望值等于没有噪音时的值。

• 在毕晓普的工作中，他将高斯噪声添加到线性模型的输入中。 在每次训练迭代中，他将从均值为零的分布 \(\epsilon \sim \mathcal{N}(0,\sigma^2)\) 的采样噪声添加到输入 \(x\) 中，从而产生扰动点 \(\mathbf{x}' = \mathbf{x} + \epsilon\) ，预期（数学期望为） \(E[\mathbf{x}'] = \mathbf{x}\)

• 在标准暂退法正则化中，通过按保留（未丢弃）的节点的分数进行规范化来消除每一层的偏差。 换言之，每个中间活性值 \(h\) 以暂退概率 \(p\) 由随机变量 \(h′\) 替换，使得 \(E(h') = E(h)\) 如下所示： $$\begin{split}\begin{aligned}
  h' =
  \begin{cases}
  0 & \text{ 概率为 } p \qquad
  \frac{h}{1-p} & \text{ 其他情况}
  \end{cases}
  \end{aligned}\end{split}$$

How do we apply Dropout to our Module?

step1.import packages

import torch 
from torch import nn 
from d2l import torch as d2l  

step2.define Drop-out Layer

def DropOutLayer(X,dropout): 
    assert 0<= dropout <=1  
    if dropout == 1:  
        return torch.zeros_like(X) 
    if dropout == 0: 
        return X 
    mask = (torch.rand(X.shape) > dropout).float() 
    return mask*X / (1-dropout)

step3.define Module's Parameters

num_inputs,num_outputs,num_hidden1,num_hidden2 = 784,10,256,256 
dropout1 ,dropout2 = .2 , .5 

step4.define classes that propagate forward

class Net(nn.Module): 
    def __init__(self,num_inputs,num_outputs,num_hidden1,num_hidden2,is_trian=True):  
        super(Net,self).__init__() 
        self.is_trian = is_trian 
        self.num_inputs = num_inputs 
        self.lin1 = nn.Linear(in_features=num_inputs,out_features=num_hidden1) 
        self.lin2 = nn.Linear(in_features=num_hidden1,out_features=num_hidden2) 
        self.lin3 = nn.Linear(in_features=num_hidden2,out_features=num_outputs) 
        self.relu = nn.ReLU() 
    def forward(self,X):  
        H1 = self.relu(self.lin1(X.reshape(-1,self.num_inputs))) 
        # Use dropout only in training mode 
        if self.is_trian == True:  
            # add the dropout layer between Layer1 and Layer2  
            H1 = DropOutLayer(H1,dropout1) 
        H2 = self.relu(self.lin2(H1)) 
        if self.is_trian == True: 
            H2 = DropOutLayer(H2,dropout2) 
        out = self.relu(self.lin3(H2))
        return out

step5.let's trying training this Model

net = Net(num_inputs,num_outputs,num_hidden1,num_hidden2) 
num_epochs ,lr ,batch_size= 10 ,0.1 ,256 
loss = nn.CrossEntropyLoss()
train_iter , test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)  
trainer = torch.optim.SGD(net.parameters(),lr=lr) 
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)

[out1:]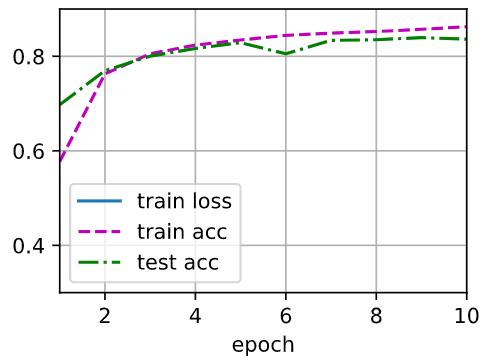

完全使用框架方法实现Deop-out Layer

# Simple implementation  
dropout1, dropout2 = 0.2, 0.5 
net = nn.Sequential( 
    nn.Flatten(), 
    nn.Linear(784,256), 
    nn.ReLU(), 
    nn.Dropout(dropout1), # 不能够在激活函数之前加，否则会损失掉一部分信息 
    nn.Linear(256,256), 
    nn.ReLU(), 
    nn.Dropout(dropout2),  
    nn.Linear(256,10), 
)

def init_weights(m): 
    if type(m) == nn.Linear: 
        nn.init.normal_(m.weight,std=0.01) 

net.apply(init_weights) 

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

[out2:]

用框架实现的 Dropout 貌似更加稳定。这里就要进行我们喜闻乐见的 \(Q&A\) 环节了

Q&A

\(Q1:\) 在我们自定义实现的Dropout层里面的 assert 关键字是什么用法？
\(A1:\) 检查条件，不符合就终止程序。 不懂看这儿

\(Q2:\) 为什么Dropout层在激活函数之后？
\(A2:\) 先来回顾下激活函数的作用：使得我们的模型非线性，或者去线性化。 线性模型经过多个线性的变换仍旧是线性模型，线性模型表达的内容十分有限。像最简单 \(X-OR\) 函数都不能够进行拟合。 其实放在激活函数之前或者之后没有区别，想要证明的可以使用前面的简便实现进行验证。

\(Q3:\) 自己实现的 class Net(nn.Model) 部分没看懂？
\(A3:\) 自己实现的Net类继承了nn.Module类，这是PyTorch中所有网络的父类。在nn.Module中有一个__call__()方法，它相当于C++中的重载()运算符，当我们执行 类名() 这种样式的语句时就会调用__call__()，而在该方法中就有调用forward()。在自定义Net类中我们def的forward()相当于重载了父类nn.Module中的forward()方法，同时自定义Net类也继承了父类的__call__()，因此在执行Net(input)这样的语句时Net类的__call__()被调用，连带着其中的forward()也被调用了，表现出来的就是使用Net(input)时forward()被运行。