Pytorch 4.4 模型选择和多项式回归

模型选择

1.1 Training Error And Generalization Error (训练误差和泛化误差)

• Training Error: 训练误差，指的是在训练数据得到的误差。
• Generalization Error：在原本的样本中抽取无限多的样本时，所计算出来的误差的期望值。一般使用测试集进行计算。

1.3 模型的复杂性

1. 简单的模型和大量的数据可能会造成训练误差和泛化误差非常接近。
2. 复杂的模型和少量的数据极有可能造成训练误差和泛化误差差距巨大，也就是泛化误差非常大，训练误差会很小的一种情况。
3. 诸如此来的等等等等 ... ...

几种影响泛化误差的因素：
(1)可调整参数的数量非常大，比如我们在用多层感知机模型训练的时候，隐藏层的单元达到惊人的 \(2^{50}\) 个的话，那么我们的模型就极有可能会过拟合。
(2)参数的取值范围很大，导致我们的模型曲线可以很“陡峭”，可以很精细的模拟我们的训练数据，容易过拟合，一般我们会引入正则化来规范我们的权重，使之不要太大或者太小。
(3)样本数量。比如样本数量少的时候就会容易Overfitting，样本数量大的时候，模型就很难Overfitting。
(4)还有很多诸如此类,但是没有介绍不代表没有，在实操的时候会遇到很多问题，但是基本上都不过上面的三个... ...

2.1模型选择

问题一，我们绝不能够使用测试集来训练数据，不然我们在测试的时候不论如何都是过拟合的，即泛化误差过大，训练误差过小。但是在现实生活中我们往往要对比较多个模型，但是我们绝不能够使用测试数据集的误差来选择模型，也不能够只通过训练数据集的误差来选择模型，所以我们一般会把数据分成三个部分：
（1）Training Dataset
（2）Testing Dataset
（3）Validation Dataset

没错，就是增加了一个验证数据集Validation Dataset，但是十分不幸的是，在机器学习中 Testing Dataset 和 Validation Dataset 的界限十分模糊，而且大多数时候人们只会将数据划分成一个训练数据集和Others。在李沐大神《DIVE INTO DEEP LEARNING》这本书中也说过，两者的界限太过于模糊，一般来说只取一个训练集和测试机即可。

2.2K折交叉验证

在我们的数据集的样本数量比较少的时候，并且我们甚至可能无法提供足够的数据来构成一个合适的验证集的时候。我们可以采用折交叉验证。
(1) 将数据划分成将数据集随机分为互斥的k个子集，为保证随机性，P次随机划分取平均。
(2) 将k个子集随机分为k-1个一组剩下一个为另一组，有k种分法。
(3) 将每一种分组结果中，k-1个子集的组当做训练集，另外一个当做测试集，这样就产生了k次预测，对其取平均。
(4) 称为p次k折交叉验证，一般取k=10。

3.1欠拟合还是过拟合？

我们还是采用举例的方式来引出过拟合和欠拟合比较合适，因为情况分为很多种，不能够很好概括。
(1) 如果泛化误差 Generalization Error 和 训练误差 Training Error (下面都用G和T来代替泛化误差和训练误差)都很大且G和T都是严丝合缝的时候，说明模型不能够很好模拟真实的情况，模型表达能力不足。欠拟合。
(2) 当T严重低于验证集误差 Validation Error (简称V) 的时候，说明泛化误差过大了，模型只对当前的数据有很好的 “普适性” ，说明模型已经过拟合了。
(3) 诸如此类 ... ...

多项式回归 Polynomial Regression

• 之所以叫做多项式回归，是为了区分之前的线性回归,但是其实实现方式和原理几乎一摸一样
  给定 \(x\) ，我们将使用以下三阶多项式来生成训练和测试数据的标签：

\[y = 5 + 1.2x - 3.4\frac{x^2}{2!} + 5.6 \frac{x^3}{3!} + \epsilon \text{ where } \epsilon \sim \mathcal{N}(0, 0.1^2).\]

step1.导入包

import torch 
import numpy as np  
import math 
from torch import nn  
from d2l import torch as d2l  

step2.生成数据

# 之所以叫做多项式回归，是为了区分之前的线性回归,但是其实实现方式和原理几乎一摸一样
max_degree = 20  # 多项式的最大阶数
n_train, n_test = 100, 100  # 训练和测试数据集大小
true_w = np.zeros(max_degree)  # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])  

features = np.random.normal(size=(n_train+n_test,1)) 
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))  # 计算features的0-3次方 返回的是[200,20]
for i in range(max_degree): # 0,1,2,3,0,0,...,0
    poly_features[:,i] /= math.gamma(i+1) # gamma(n) = (n-1)!  每一个项除以一个它的阶乘 
labels = np.dot(poly_features, true_w) # (200,)
labels += np.random.normal(scale=0.1, size=labels.shape) # 加上噪音 𝜖

step3.将numpy.ndarray转换成torch.tensor

# 将numpy.ndarray转换成为tensor 
true_w, features, poly_features, labels = [torch.tensor(x, dtype=
    torch.float32) for x in [true_w, features, poly_features, labels]]

features[:2], poly_features[:2, :], labels[:2] # 验证数据是正确的 

def evaluate_loss(net, data_iter, loss):  #@save
    """评估给定数据集上模型的损失"""
    metric = d2l.Accumulator(2)  # 损失的总和,样本数量
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())
    return metric[0] / metric[1]

step4.定义训练函数

# 定义训练函数 
def train(train_features, test_features, train_labels, test_labels,
          num_epochs=400):
    loss = nn.MSELoss(reduction='none')
    input_shape = train_features.shape[-1] 
    # 不设置偏置，因为我们已经在多项式特征中实现了它
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
    batch_size = min(10, train_labels.shape[0])
    train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
                               batch_size, is_train=False)
    trainer = torch.optim.SGD(net.parameters(), lr=0.001)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
                                     evaluate_loss(net, test_iter, loss)))
    print('weight:', net[0].weight.data.numpy())

step5.训练模型

使用三项多项式来训练

# 从多项式特征中选择前4个维度，即1,x,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
      labels[:n_train], labels[n_train:]) # 很简单，都是选取前面的100然后后面的100  

weight: [[ 4.9989753 1.1796033 -3.3834207 5.620317 ]]

使用线性模型来训练

# 用线性模型来训练我们的样本 欠拟合，模型表达能力不足 
train(poly_features[:n_train, :2],poly_features[n_train: ,:2],labels[:n_train],labels[n_train:],num_epochs=400)

weight: [[3.168832 4.7659645]]

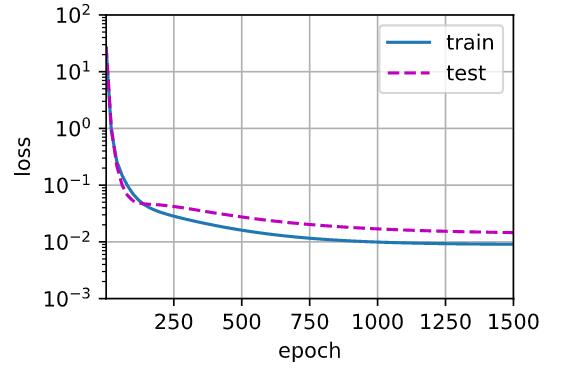
使用全部的多项式来训练我们模型

# 从多项式特征中选取所有维度 测试误差较大，但是训练误差已经很小了，说明已经过拟合了
train(poly_features[:n_train, :], poly_features[n_train:, :],
      labels[:n_train], labels[n_train:], num_epochs=1500)

weight: [[ 4.9898410e+00 1.2610230e+00 -3.3627594e+00 5.2209153e+00
-1.4960654e-02 1.1311897e+00 -1.2000563e-01 3.2521218e-01
2.3846129e-01 1.5138565e-01 -1.3304563e-01 5.2104637e-02
1.9422704e-01 -4.0500900e-06 1.6017137e-01 -5.8273338e-02
-1.9491109e-01 -2.0387647e-01 -9.3304843e-02 -1.9399533e-01]]

参考：np.power() 用法: https://blog.csdn.net/qq_36512295/article/details/98472358
[官方表述] #@save 的用法 ：
If you are following d2l pytorch book like me then the explanation is given at page 68 Chapter 2. "Note that the comment #@save is a special mark where the following function, class, or statements are saved in the d2l package so later they can be directly invoked (e.g., d2l.use_svg_display()) without being redefined.