矩阵求导
矩阵求导
矩阵求导1 简单求导
假设我有A和B两个张量(可以是1x1的标量也可以是向量或者矩阵),所谓矩阵求导 , 就是矩阵A当中的每一个元素对B中的每一元素进行求导,所以求到之后的张量的元素的个数有以下情形:

那么现在我们来复习一下函数的几种形式: 1️⃣标量函数:,像这种称为标量函数。
2️⃣那么向量函数或者矩阵函数的定义就显而易见了,刑如的函数称为向量函数,就好比如:
矩阵求导有两个法则:分母、分子布局,但是在这一篇文章中我们都会以分母布局作为演示。用简单一点的话来说就是,求导出来的形状和分母的形状相同。


分子布局虽然没有说,但是按照上面讲的定义,就是求导出来的形状都会与分子的形状相同。
矩阵求导2 公式求导
1.求导 ----->

2.求导 ----->

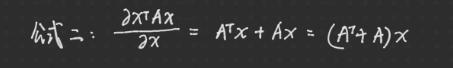
3.最小二乘法:求导 ----->

矩阵求导3 常用的矩阵求导公式介绍
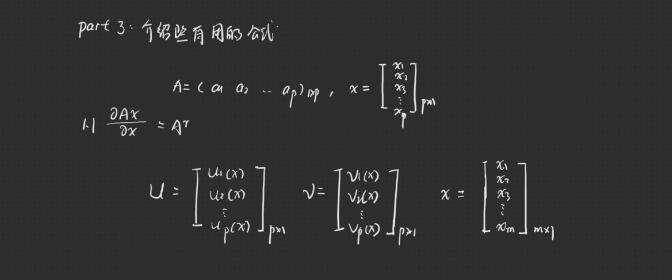

总结
1.矩阵求导的结果有很多种,这要看使用的是什么求导的方式:分子/分母/混合布局等等。所以不同的人求导出来的结果不一样很正常。
2.使用什么布局没有什么优劣之分,但是要注意前后求导的一致性,比如前面一条公式我使用分子求导,后面一条公式我却用了分母求导,这样得到的结果相乘或者做一些其他运算必然会出错。
3.我们要学会反推别人的求导方式,我们可以通过维度上的信息进行判断,或者直接按照别人的公式推导一次,因为在大多数论文中都是没有说明是分子/分母布局的。
4.我这里推荐几个矩阵求导讲的特别好的大佬:
B站:空狐公子
个人博客:zdaiot
维基百科(矩阵求导)
Po-chen Wu ppt
码字不易,创作辛苦,请点个赞吧。(如果有错误的话请斧正,感谢!!你的支持是我最大的动力)
posted on 2021-12-14 23:57 YangShusen' 阅读(8862) 评论(0) 编辑 收藏 举报


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 终于写完轮子一部分:tcp代理 了,记录一下
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理