冒泡排序
1 //冒泡排序
2 //////////////////////////////////////////////////////////////////////////
3 void BubleSort(int a[],int n)
4 {
5 int temp;
6 bool flag=false;
7 for (int i=0;i<n;i++)
8 {
9 flag=true;
10 for (int j=0;j<n-i-1;j++)
11 {
12 if(a[j]>a[j+1])
13 {
14 temp=a[j];
15 a[j]=a[j+1];
16 a[j+1]=temp;
17 flag=false;
18 }
19 }
20 if(flag) break;
21 }
22 }
冒泡排序的时间复杂度为O(n²),在数据比较小的情况下各个算法效率差不多。
希尔排序:

void ShellSort(int array[],int length)
2
3 {
4
5 int d = length/2; //设置希尔排序的增量
6 int i ;
7 int j;
8 int temp;
9 while(d>=1)
10 {
11 for(i=d;i<length;i++)
12 {
13 temp=array[i];
14 j=i-d;
15 while(j>=0 && array[j]>temp)
16 {
17 array[j+d]=array[j];
18 j=j-d;
19 }
20 array[j+d] = temp;
21 }
22 //Display(array,10);
23 d= d/2; //缩小增量
24 }
25 }
其效率很多时候并不输给快速排序其时间复杂度为O(nlogn)。
快速排序:
1 //快速排序
2 ///////////////////////////////////////
3 void Swap(int &a,int &b)
4 {
5 int temp;
6 temp=a;
7 a=b;
8 b=temp;
9 }
10
11 int Partition(int a[],int p,int r)
12 {
13 int i=p;
14 int j=r+1;
15 int x=a[p];
16 while (true)
17 {
18 while(a[++i]<x&&i<r);
19 while(a[--j]>x);
20 if (i>=j)break;
21 Swap(a[j],a[i]);
22
23 }
24 a[p]=a[j];
25 a[j]=x;
26 return j;
27 }
28
29 void QuickSort(int a[],int p,int r)
30 {
31 if (p<r)
32 {
33 int q=Partition(a,p,r);
34 QuickSort(a,p,q-1);
35 QuickSort(a,q+1,r);
36 }
37 }
正如其名快速排序,其效率也是比较高的,时间复杂度为O(nlogn)。难点还是递归的理解!
插入排序:
1 //插入排序
2 //////////////////////////////////////////////////////////////////
3 void Insert(int *a,int n)
4 {
5 int i=n-1;
6 int key=a[n];//需要插入的元素
7 while ((i>=0)&&(key<a[i]))
8 {
9 a[i+1]=a[i]; //比key大的元素往后一个位置,空出插入key的位置
10 i--;
11 }
12 a[i+1]=key;//找到位置插入元素
13 return;
14 }
15
16 //由于递归的原因数太大了栈可能会溢出
17 void InsertionSort(int *a,int n)
18 {
19 if (n>0)
20 {
21 InsertionSort(a,n-1);
22 Insert(a,n);
23 }
24 else return;
25 }
算法效率和冒泡排序相差无几,时间复杂度为O(n²)。
堆排序:

1 //堆排序
2 ////////////////////////////////////////////////////////////////////////////
3 int Parent(int i)
4 {
5 return i/2;
6 }
7 int Left(int i)
8 {
9 return 2*i;
10 }
11 int Right(int i)
12 {
13 return 2*i+1;
14 }
15
16 //把以第i个节点给子树的根的子树调整为堆
17 void MaxHeap(int *a,int i,int length)
18 {
19 int L=Left(i);
20 int R=Right(i);
21 int temp;
22 int largest; //记录子树最大值的下表,值可能为根节点下标、左子树下表、右子树下标
23 if (L<=length&&a[L-1]>a[i-1]) //length是递归返回的条件
24 {
25 largest=L;
26 }
27 else largest=i;
28 if (R<=length&&a[R-1]>a[largest-1]) //length是递归返回的条件
29 largest=R;
30 if (largest!=i)
31 {
32 temp=a[i-1];
33 a[i-1]=a[largest-1];
34 a[largest-1]=temp;
35 MaxHeap(a,largest,length);
36 }
37 }
38
39 void BuildMaxHeap(int *a,int length)
40 {
41
42 for (int i=length/2;i>=1;i--)
43 MaxHeap(a,i,length);
44 }
45
46 void HeapSort(int *a,int length)
47 {
48 BuildMaxHeap(a,length);
49 for (int i=length;i>0;i--)
50 {
51 int temp;
52 temp=a[i-1];
53 a[i-1]=a[0];
54 a[0]=temp;
55 length-=1;
56 MaxHeap(a,1,length);
57 }
58 }

通过使用大根堆来排序,排序过程中主要的动作就是堆的调整。每次把堆的根节点存入到堆的后面,然后把最后一个节点交换到根节点的位置,然后又调整为新的堆。这样不断重复这个步骤就能把把一个数组排列的有序,时间复杂度为O(nlogn)。
最后一种是比较特别的基数排序(属于分配式排序,前几种属于比较性排序)又称“桶子法”:
基本思想是通过键值的部分信息分配到某些桶中,藉此达到排序的作用,基数排序属于稳定的排序,其时间复杂度为O(nlog(r)m),r为所采取的的基数,m为堆的个数,在某些情况下基数排序法的效率比其他比较性排序效率要高。

1 //基数排序
2 /////////////////////////////////////////////////
3 int GetMaxTimes(int *a,int n)
4 {
5 int max=a[0];
6 int count=0;
7 for (int i=1;i<n;i++)
8 {
9 if(a[i]>max)
10 max=a[i];
11 }
12 while(max)
13 {
14 max=max/10;
15 count++;
16 }
17 return count;
18 }
19
20 void InitialArray(int *a,int n)
21 {
22 for (int i=0;i<n;i++)
23 a[i]=0;
24 }
25
26 // void InitialArray1(int a[][],int m,int n)
27 // {
28 // for (int i=0;i<m;i++)
29 // for (int j=0;j<n;j++)
30 // a[i][j]=0;
31 // }
32
33 void RadixSort(int *a,int n)
34 {
35 int buckets[10][10000]={0};
36 int times=GetMaxTimes(a,n);
37 int index,temp;
38 int record[10]={0};
39 for (int i=0;i<times;i++)
40 {
41 int count=0;
42 temp=pow(10,i);//index=(a[j]/temp)%10;用来从低位到高位分离
43 for (int j=0;j<n;j++)
44 {
45 index=(a[j]/temp)%10;
46 buckets[index][record[index]++]=a[j];
47 }
48 //把桶中的数据按顺序还原到原数组中
49 for(int k=0;k<10;k++)
50 for (int m=0;m<100000;m++)
51 {
52 if(buckets[k][m]==0)break;
53 else
54 {
55 a[count++]=buckets[k][m];
56 //cout<<buckets[k][m]<<" ";
57 }
58 }
59 //重新初始化桶,不然前后两次排序之间会有影响
60 //buckets[10][10000]={0};
61 //record[10]={0};
62 //InitialArray1(buckets,10,10000);
63 for (k=0;k<10;k++)
64 for (int m=0;m<100000;m++)
65 {
66 if(buckets[k][m]==0)break;
67 else buckets[k][m]=0;
68 }
69 InitialArray(record,10);
70 }
71 }


数据量为100:
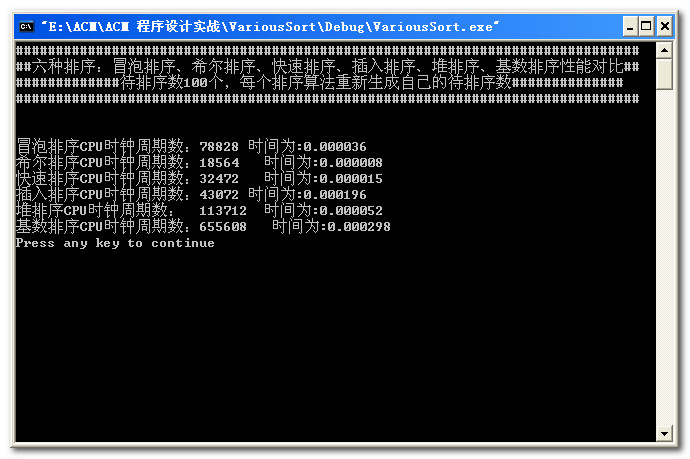
数据量为1000:
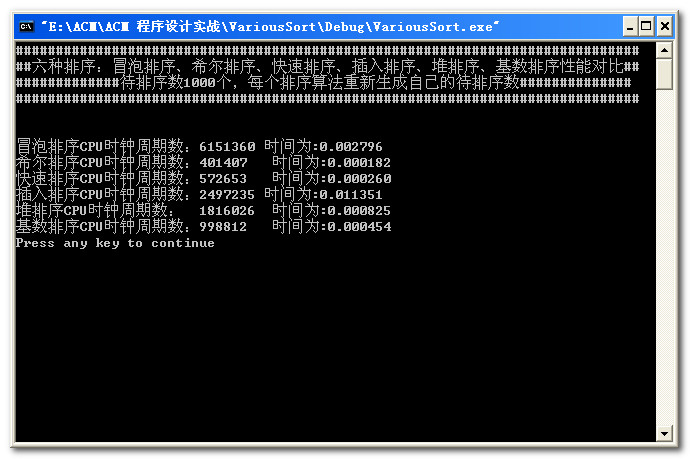
数据量为10000:
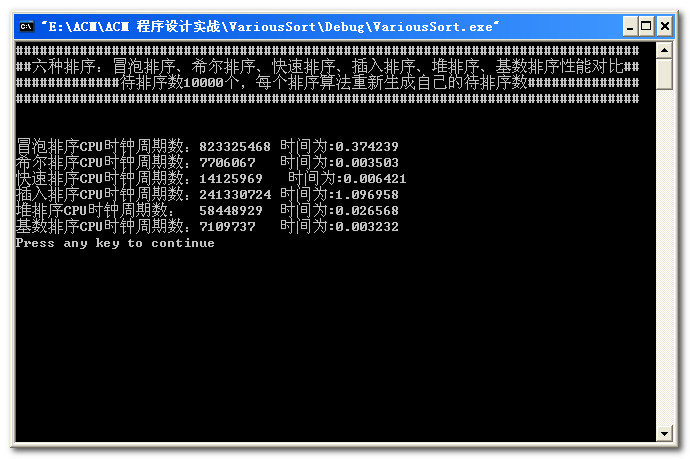
数据量为15000:
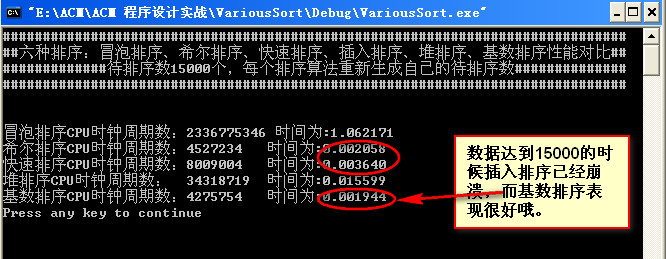
数据量为20000:
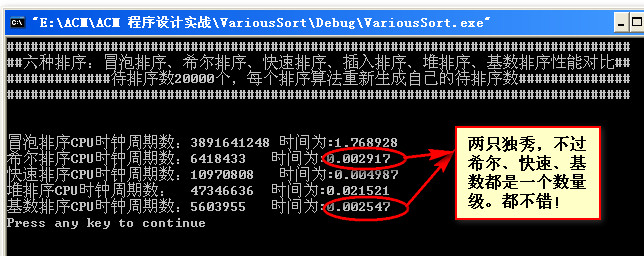
数据量为50000:
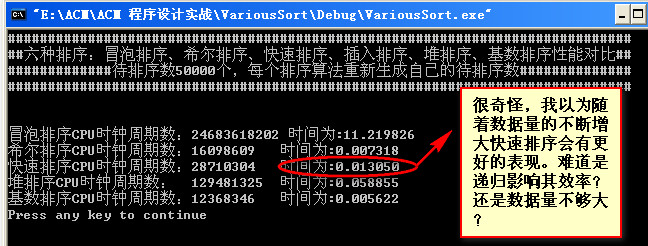
数据量为90000:

数据量为80000:
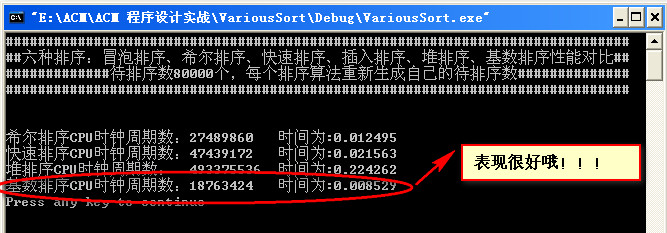
越来越兴奋了:


接下来想测一测10亿是神马情况程序直接挂了,然后测一测5亿然后就死机了,然后就木有然后了,我写了一半的博客!!!!!~~o(>_<)o ~~!!!!!~~o(>_<)o ~~!!!!!~~o(>_<)o ~~
后面测了一下5亿!本来录了一段小视频的,但是上传不了。这里就说出答案吧:5亿数据时,快速排序也挂了,只有希尔排序一直在健壮的运行,运行时间大概为120s左右。
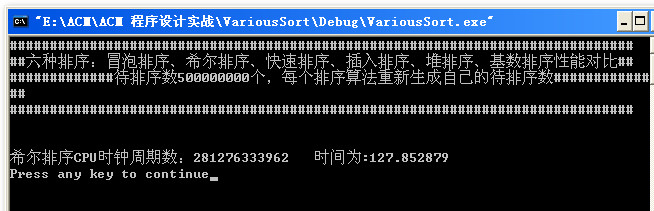
大概分析了一下数据所占的内存:
首先5亿个数据占多少内存?
(50000000*4)/(pow(1024,3))=1.86G
我的电脑内存为3G左右,除去操作系统和软件大约占了20%3G=0.6G。
3-0.6-1.86=0.54G剩余
0.54*pow(1024,3)/4=144955146剩余内存还可以计算1亿多个数据,
所以我的电脑一共能同时排序644955146个数据。这就是为什么排序10亿数据时程序崩溃的原因,因为没有这么多内存分配给程序使用。
然而我实际测了一下实际上达不到6亿,5.5亿就崩溃了,原因有待后续考察!

















