算法模板
基本算法
位
# << 左移
二进制左移,填充0
3 << 2 === 3 * 2 * 2
# >> 右移
正数填充0,负数填充1,因此,右移负数始终为负数,正数始终为正数
27 >> 3 === 24 / 3 / 3
# >>> 无符号右移
正数右移补0, 负数也补0,因此负数会转为正数,负数会达到int最大值
-1 >>> 1 === 2147483647
16 >>> 2 === 16/2/2
# & 与
都为1时为1,其余情况为0
# | 或
有一个1则值为1,全为0值为0
# ^ 异或
相同为0, 不同为1
# ~
0变1,1变0
# 原码,反码,补码
• 第一位0,1决定正负,其余位是数字的大小,绝对值相同的数字除第一位外的其余位是相同
• 正数:原码、反码、补码全部相同
• 负数:
○ 反码:除第一位外,其余位取反
补码:反码+1
二分
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
double bsearch_3(double l, double r)
{
const double eps = 1e-6;
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
高精
高精度加法
#include <iostream>
#include <vector>
using namespace std;
vector<int> add(vector<int> a, vector<int> b) {
vector<int> c;
int la = a.size(), lb = b.size();
if (la < lb) return add(b, a);
int t = 0;
for (int i = 0; i < la; ++i) {
t += a[i];
if (i < lb) t += b[i];
c.push_back(t % 10);
t /= 10;
}
if (t) c.push_back(t);
return c;
}
int main(void) {
vector<int> a, b;
string A, B;
cin >> A >> B;
for (int i = A.size() - 1; i >= 0; --i) a.push_back(A[i] - '0');
for (int i = B.size() - 1; i >= 0; --i) b.push_back(B[i] - '0');
vector<int> c = add(a, b);
for (int i = c.size() - 1; i >= 0; --i) cout << c[i];
return 0;
}
高精度减法
#include <iostream>
#include <vector>
using namespace std;
bool cmp(vector<int> a, vector<int> b) {
if (a.size() != b.size()) return a.size() > b.size();
for (int i = a.size() - 1; i >= 0; --i)
if (a[i] != b[i]) return a[i] > b[i];
return true;
}
vector<int> sub(vector<int> a, vector<int> b) {
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); ++i) {
t = a[i] - t;
if (i < b.size()) t -= b[i];
c.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
int main(void) {
string A, B;
cin >> A >> B;
vector<int> a, b, c;
for (int i = A.size() - 1; i >= 0; --i) a.push_back(A[i] - '0');
for (int i = B.size() - 1; i >= 0; --i) b.push_back(B[i] - '0');
if (cmp(a, b)) c = sub(a, b);
else c = sub(b, a), cout << '-';
for (int i = c.size() - 1; i >= 0; --i) cout << c[i];
return 0;
}
高精度乘法
#include <iostream>
#include <vector>
using namespace std;
vector<int> mul(vector<int> a, int b) {
vector<int> c;
int t = 0;
for (int i = 0; i < a.size() || t; ++i) {
if (i < a.size()) t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
int main(void) {
string A;
int b;
cin >> A >> b;
vector<int> a;
for (int i = A.size() - 1; i >= 0; --i) a.push_back(A[i] - '0');
vector<int> c = mul(a, b);
for (int i = c.size() - 1; i >= 0; --i) cout << c[i];
return 0;
}
高精度除法
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> div(vector<int> a, int b, int &r) {
vector<int> c;
r = 0;
for (int i = a.size() - 1; i >= 0; --i) {
r = r * 10 + a[i];
c.push_back(r / b);
r %= b;
}
reverse(c.begin(), c.end());
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
int main(void) {
string A;
int b;
vector<int> a, c;
cin >> A >> b;
for (int i = A.size() - 1; i >= 0; --i) a.push_back(A[i] - '0');
int r;
c = div(a, b, r);
for (int i = c.size() - 1; i >= 0; --i) cout << c[i];
cout << endl << r;
return 0;
}
双指针
最长连续不重复子序列
/*给定一个长度为 n 的整数序列,请找出最长的不包含重复的数的连续区间,输出它的长度。*/
#include <iostream>
using namespace std;
const int N = 100010;
int a[N], st[N], n;
int main(void) {
cin >> n;
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
int res = 0;
for (int i = 1, j = 1; i <= n; ++i) {
st[a[i]]++;
while (j < i && st[a[i]] > 1) st[a[j++]]--;
res = max(res, i - j + 1);
}
cout << res;
return 0;
}
数组元素的目标和
/* 数组a,b递增,求ai+bj==x时i,j下标,注意:模板规定下标从0开始 */
#include <iostream>
using namespace std;
const int N = 100010;
int a[N], b[N];
int n, m, x;
int main(void) {
scanf("%d%d%d", &n, &m, &x);
for (int i = 1; i <= n; ++i) scanf("%d", a + i);
for (int i = 1; i <= m; ++i) scanf("%d", b + i);
for (int i = 1, j = m; i <= n; ++i) {
while (j >= 1 && a[i] + b[j] > x) j--;
if (a[i] + b[j] == x) {
printf("%d %d", i - 1, j - 1);
break;
}
}
return 0;
}
判断子序列
数组a是否为数组b的子序列(指按原有次序排列)
#include <iostream>
using namespace std;
const int N = 100010;
int a[N], b[N], n, m;
int main(void) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", a + i);
for (int i = 1; i <= m; ++i) scanf("%d", b + i);
int i = 1;
for (int j = 1; j <= m; ++j) {
if (a[i] == b[j]) i++;
}
if (i == n + 1) puts("Yes");
else puts("No");
return 0;
}
离散化
求区间和(保序)
记得开多倍数组
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
vector<PII> add, query;
vector<int> all;
int a[N * 3], s[N * 3];
int n, q;
int find(int x) {
int l = 0, r = all.size() - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (all[mid] < x) l = mid;
else r = mid - 1;
}
return r + 1;
}
int main(void) {
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; ++i) {
int x, v;
scanf("%d%d", &x, &v);
add.push_back({x, v});
all.push_back(x);
}
for (int i = 1; i <= q; ++i) {
int l, r;
scanf("%d%d", &l, &r);
query.push_back({l, r});
all.push_back(l);
all.push_back(r);
}
sort(all.begin(), all.end());
all.erase(unique(all.begin(), all.end()), all.end());
for (int i = 0; i < add.size(); ++i) {
int x = add[i].first, v = add[i].second;
x = find(x);
a[x] += v;
}
for (int i = 1; i <= all.size(); ++i) s[i] = s[i - 1] + a[i];
for (int i = 0; i < query.size(); ++i) {
int l = query[i].first, r = query[i].second;
l = find(l), r = find(r);
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}
其他
区间合并
给定 n个区间[l, r],要求合并所有有交集的区间。
#include <iostream>
#include <vector>
#include <algorithm>
#define l first
#define r second
using namespace std;
typedef pair<int, int> PII;
vector<PII> segs;
int n;
int merge() {
vector<PII> res;
int l = -2e9, r = -2e9;
for (int i = 0; i < segs.size(); ++i) {
PII t = segs[i];
if (r < t.l) {
if (r != -2e9) res.push_back({l, r});
l = t.l, r = t.r;
}
else
r = max(r, t.r);
}
if (l != -2e9) res.push_back({l, r});
return res.size();
}
int main(void) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int l, r;
scanf("%d%d", &l, &r);
segs.push_back({l, r});
}
sort(segs.begin(), segs.end());
cout << merge();
return 0;
}
动态中位数
依次读入一个整数序列,每当已经读入的整数个数为奇数时,输出已读入的整数构成的序列的中位数。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
int n, m;
scanf("%d%d", &m, &n);
printf("%d %d\n", m, (n + 1) / 2);
priority_queue<int> down;
priority_queue<int, vector<int>, greater<int>> up;
int cnt = 0;
for (int i = 1; i <= n; i ++ )
{
int x;
scanf("%d", &x);
if (down.size() == 0 || x <= down.top()) down.push(x);
else up.push(x);
if (down.size() > up.size() + 1) up.push(down.top()), down.pop();
if (up.size() > down.size()) down.push(up.top()), up.pop();
if (i % 2)
{
printf("%d ", down.top());
if ( ++ cnt % 10 == 0) puts("");
}
}
if (cnt % 10) puts("");
}
return 0;
}
增减序列
给定一个长度为 n 的数列 a1,a2,…,an,每次可以选择一个区间 [l,r],使下标在这个区间内的数都加一或者都减一。
求至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列可能有多少种。
第一行输出最少操作次数。
第二行输出最终能得到多少种结果。
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 100010;
int a[N], d[N];
int n;
int main(void) {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
for (int i = 1; i <= n; ++i) d[i] = a[i] - a[i - 1];
LL p = 0, q = 0;
for (int i = 2; i <= n; ++i)
if (d[i] > 0) p += d[i];
else q -= d[i];
cout << max(p, q) << endl;
cout << (abs(p - q) + 1) ;
return 0;
}
数据结构
表达式求值
**求(2+2)*(1+1) 形式的中序表达式 **
#include <iostream>
#include <unordered_map>
#include <stack>
using namespace std;
string s;
stack<int> nums;
stack<char> op;
void eval() {
char c = op.top(); op.pop();
int b = nums.top(); nums.pop();
int a = nums.top(); nums.pop();
int x = 0;
if (c == '+') x = a + b;
if (c == '-') x = a - b;
if (c == '*') x = a * b;
if (c == '/') x = a / b;
nums.push(x);
}
int main(void) {
cin >> s;
unordered_map<char, int> pr = { {'+', 1}, {'-', 1}, {'*', 2}, {'/', 2} };
for (int i = 0; i < s.size(); ++i) {
char c = s[i];
if (isdigit(c)) {
int x = 0, j = i;
while (j < s.size() && isdigit(s[j])) {
x = x * 10 + s[j] - '0';
j++;
}
i = j - 1;
nums.push(x);
} else {
if (c == '(') op.push('(');
else if (c == ')') {
while (op.size() && op.top() != '(') eval();
op.pop();
} else {
while (op.size() && op.top() != ')' && pr[op.top()] >= pr[c]) eval();
op.push(c);
}
}
}
while (op.size()) eval();
cout << nums.top();
return 0;
}
单调栈
输入n个数,输出每个数左边第一个比它小的数,不存在则输出-1
#include <iostream>
#include <stack>
using namespace std;
stack<int> st;
int main(void) {
int n;
scanf("%d", &n);
while (n--) {
int x;
scanf("%d", &x);
while (st.size() && st.top() >= x) st.pop();
if (st.size()) printf("%d ", st.top());
else printf("-1 ");
st.push(x);
}
return 0;
}
单调队列
滑动窗口求最大&最小
#include <iostream>
using namespace std;
const int N = 1000010;
int a[N], q[N];
int n, k;
int main(void) {
scanf("%d%d", &n, &k);
for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
/* k中求最小 */
int hh = 0, tt = -1; // hh头,tt尾
for (int i = 0; i < n; ++i) {
if (hh <= tt && i - k + 1 > q[hh]) hh++;
while (hh <= tt && a[q[tt]] >= a[i]) tt--;
q[++tt] = i;
if (i - k + 1 >= 0) printf("%d ", a[q[hh]]);
}
puts("");
/* k中求最大 */
hh = 0, tt = -1;
for (int i = 0; i < n; ++i) {
if (hh <= tt && i - k + 1 > q[hh]) hh++;
while (hh <= tt && a[q[tt]] <= a[i]) tt--;
q[++tt] = i;
if (i - k + 1 >= 0) printf("%d ", a[q[hh]]);
}
return 0;
}
KMP
求P在S中所有出现位置的起始下标
#include <iostream>
using namespace std;
const int N = 100010, M = 1000010;
int n, m;
char p[N], s[M];
int ne[N];
int main(void) {
cin >> n >> p + 1;
cin >> m >> s + 1;
// next[]
for (int i = 2, j = 0; i <= n; ++i) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
//kmp
for (int i = 1, j = 0; i <= m; ++i) {
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j++;
if (j == n) {
cout << i - n + 1 - 1 << ' ';
j = ne[j];
}
}
return 0;
}
Trie
Trie字符串统计
统计字符串在集合中出现了多少次
输入的n个操作中,'I'表示插入字符串,'Q'表示查询字符串
#include <iostream>
using namespace std;
const int N = 20010;
int son[N][26], cnt[N], idx;
void insert(char str[]) {
int p = 0;
for (int i = 0; str[i]; ++i) {
int u = str[i] - 'a';
if (!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
cnt[p]++;
}
int query(char str[]) {
int p = 0;
for (int i = 0; str[i]; ++i) {
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
int main(void) {
int n;
scanf("%d", &n);
char str[N];
while (n--) {
char op[2];
scanf("%s%s", op, str);
if (*op == 'I')
insert(str);
else {
printf("%d\n", query(str));
}
}
return 0;
}
最大异或对
在n个数中,选两个数进行异或运算,求最大值
(相同为0,不同为1)
#include <iostream>
using namespace std;
const int N = 100010, M = 31 * N;
int son[M][2], idx;
void insert(int x) {
int p = 0;
for (int i = 31; i >= 0; --i) {
int u = x >> i & 1;
if (!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
}
int query(int x) {
int p = 0;
int res = 0;
for (int i = 31; i >= 0; --i) {
int u = x >> i & 1;
if (son[p][!u]) {
p = son[p][!u];
res = res * 2 + !u;
} else {
p = son[p][u];
res = res * 2 + u;
}
}
return res;
}
int main(void) {
int n;
scanf("%d", &n);
int res = 0;
while (n--) {
int x;
scanf("%d", &x);
insert(x);
int t = query(x);
res = max(res, t ^ x);
}
printf("%d", res);
return 0;
}
并查集
路径压缩
int p[N], d[N];
int find(int x) {
if (p[x] != x) {
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
字符串哈希
输入字符串长度n和字符串s,给出q个询问[l1, r1],[l2,r2],判断两区间的字符串是否完全相同
#include <iostream>
using namespace std;
typedef unsigned long long ULL;
const int N = 100010, P = 131;
char s[N];
ULL sum[N], p[N];
ULL get(int l, int r){
return sum[r] - sum[l - 1] * p[r - l + 1];
}
int main(void) {
int n, q;
cin >> n >> q;
cin >> s + 1;
p[0] = 1;
for (int i = 1; i <= n; ++i) {
p[i] = p[i - 1] * P;
sum[i] = sum[i - 1] * P + s[i];
}
while (q--) {
int a, b, x, y;
cin >> a >> b >> x >> y;
if (get(a, b) == get(x, y)) puts("Yes");
else puts("No");
}
return 0;
}
线段树
最大值
给定一个正整数数列 a1,a2,…,an,每一个数都在 0∼p−1 之间。
可以对这列数进行两种操作:
添加操作:向序列后添加一个数,序列长度变成 n+1;
询问操作:询问这个序列中最后 L 个数中最大的数是多少。
程序运行的最开始,整数序列为空。
一共要对整数序列进行 m 次操作。
写一个程序,读入操作的序列,并输出询问操作的答案。
#include <iostream>
using namespace std;
const int N = 200010;
struct Node {
int l, r;
int v;
} tr[N * 4];
int m, p;
void pushup(int u) {
tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) return ;
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
}
int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else return max(query(u << 1, l, r), query(u << 1 | 1, l, r));
}
void modify(int u, int x, int v) {
if (tr[u].l == x && tr[u].r == x) tr[u].v = v;
else {
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(u << 1, x, v);
else modify(u << 1 | 1, x, v);
pushup(u);
}
}
int main(void) {
cin >> m >> p;
build(1, 1, m);
int n = 0;
int last = 0;
while (m--) {
char op[2];
int x;
scanf("%s%d", op, &x);
if (op[0] == 'Q') {
last = query(1, n - x + 1, n);
printf("%d\n", last);
}
else {
n++;
modify(1, n, (last + x) % p);
}
}
}
区间最大子段和
给定长度为 N 的数列 A,以及 M 条指令,每条指令可能是以下两种之一:
1 x y,查询区间 [x,y] 中的最大连续子段和
2 x y,把 A[x] 改成 y。
对于每个查询指令,输出一个整数表示答案。
#include <iostream>
using namespace std;
const int N = 500010;
struct Node {
int l, r;
int tmax, lmax, rmax, sum;
} tr[N * 4];
int n, q;
int w[N];
void pushup(Node &u, Node &l, Node &r) {
u.sum = l.sum + r.sum;
u.lmax = max(l.lmax, l.sum + r.lmax);
u.rmax = max(r.rmax, r.sum + l.rmax);
u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
}
void pushup(int u) {
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(int u, int l, int r) {
if (l == r) tr[u] = {r, r, w[r], w[r], w[r], w[r]};
else {
tr[u] = {l , r};
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
Node query(int u, int l, int r) {
if (tr[u].l >= l && tr[u]. r <= r) return tr[u];
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else {
Node res;
Node left = query(u << 1, l, r);
Node right = query(u << 1 | 1, l, r);
pushup(res, left, right);
return res;
}
}
void modify(int u, int x, int v) {
if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v ,v ,v};
else {
int mid = tr[u].l + tr[u]. r >> 1;
if (x <= mid) modify(u << 1, x, v);
else modify(u << 1 | 1, x, v);
pushup(u);
}
}
int main(void) {
// freopen("1.txt", "r", stdin);
cin >> n >> q;
for (int i= 1; i <= n; ++i) scanf("%d", &w[i]);
build(1, 1, n);
while (q--) {
int k, x, y;
cin >> k >>x >>y;
if (k == 1) {
if (x > y) swap(x, y);
printf("%d\n", query(1, x, y).tmax);
}
else modify(1, x, y);
}
return 0;
}
区间最大公约数
给定一个长度为 N 的数列 A,以及 M 条指令,每条指令可能是以下两种之一:
C l r d,表示把 A[l],A[l+1],…,A[r] 都加上 d。
Q l r,表示询问 A[l],A[l+1],…,A[r] 的最大公约数(GCD)。
对于每个询问,输出一个整数表示答案。
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 500010;
struct Node
{
int l, r;
LL sum, d;
}tr[N * 4];
LL w[N];
int n, q;
LL gcd(LL a, LL b)
{
return b ? gcd(b, a % b) : a;
}
void pushup(Node &u, Node &l, Node &r)
{
u.sum = l.sum + r.sum;
u.d = gcd(l.d, r.d);
}
void pushup(int u)
{
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(int u, int l, int r)
{
if (l == r) {
LL d = w[r] - w[r - 1];
tr[u] = {l, r, d, d};
}
else {
tr[u] = {l, r};
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int x, LL v) // add v in x
{
if (tr[u].l == x && tr[u].r == x) {
LL d = tr[u].sum + v;
tr[u] = {x, x, d, d};
}
else {
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(u << 1, x, v);
else modify(u << 1 | 1, x, v);
pushup(u);
}
}
Node query(int u, int l, int r)
{
if (tr[u].l >= l && tr[u].r <= r) return tr[u];
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else {
Node left = query(u << 1, l, r);
Node right = query(u << 1 | 1, l, r);
Node res;
pushup(res, left, right);
return res;
}
}
int main(void)
{
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; ++i) scanf("%lld", &w[i]);
build(1, 1, n);
while (q--) {
char op[2];
int l, r;
scanf("%s%d%d", op, &l, &r);
if (*op == 'C') {
LL d;
scanf("%lld", &d);
modify(1, l, d);
if (r + 1 <= n) modify(1, r + 1, -d);
}
else {
Node left = query(1, 1, l);
Node right = {0, 0, 0, 0};
if (l + 1 <= r) right = query(1, l + 1, r);
LL d = gcd(left.sum, right.d);
printf("%lld\n", abs(d));
}
}
return 0;
}
图论
知识结构

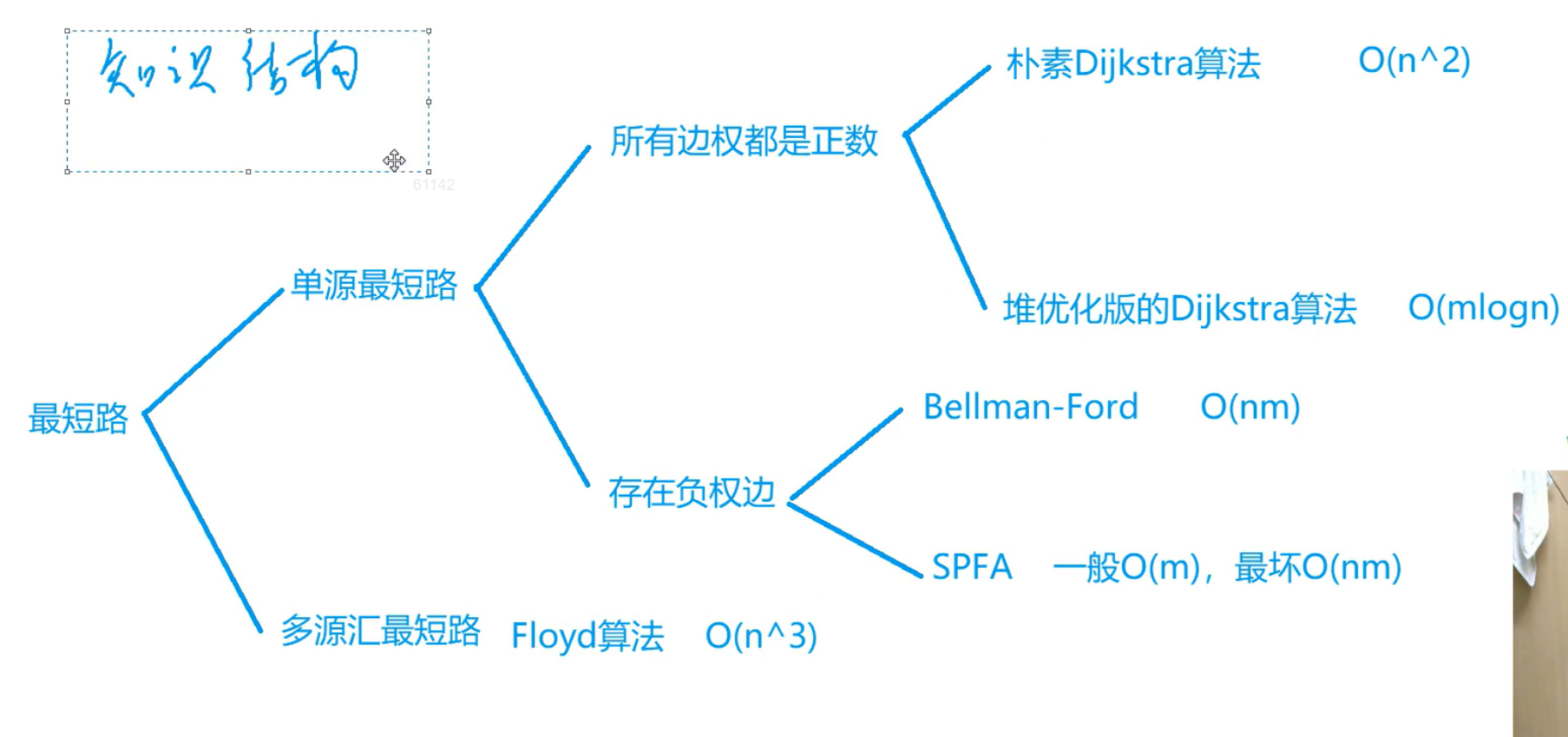
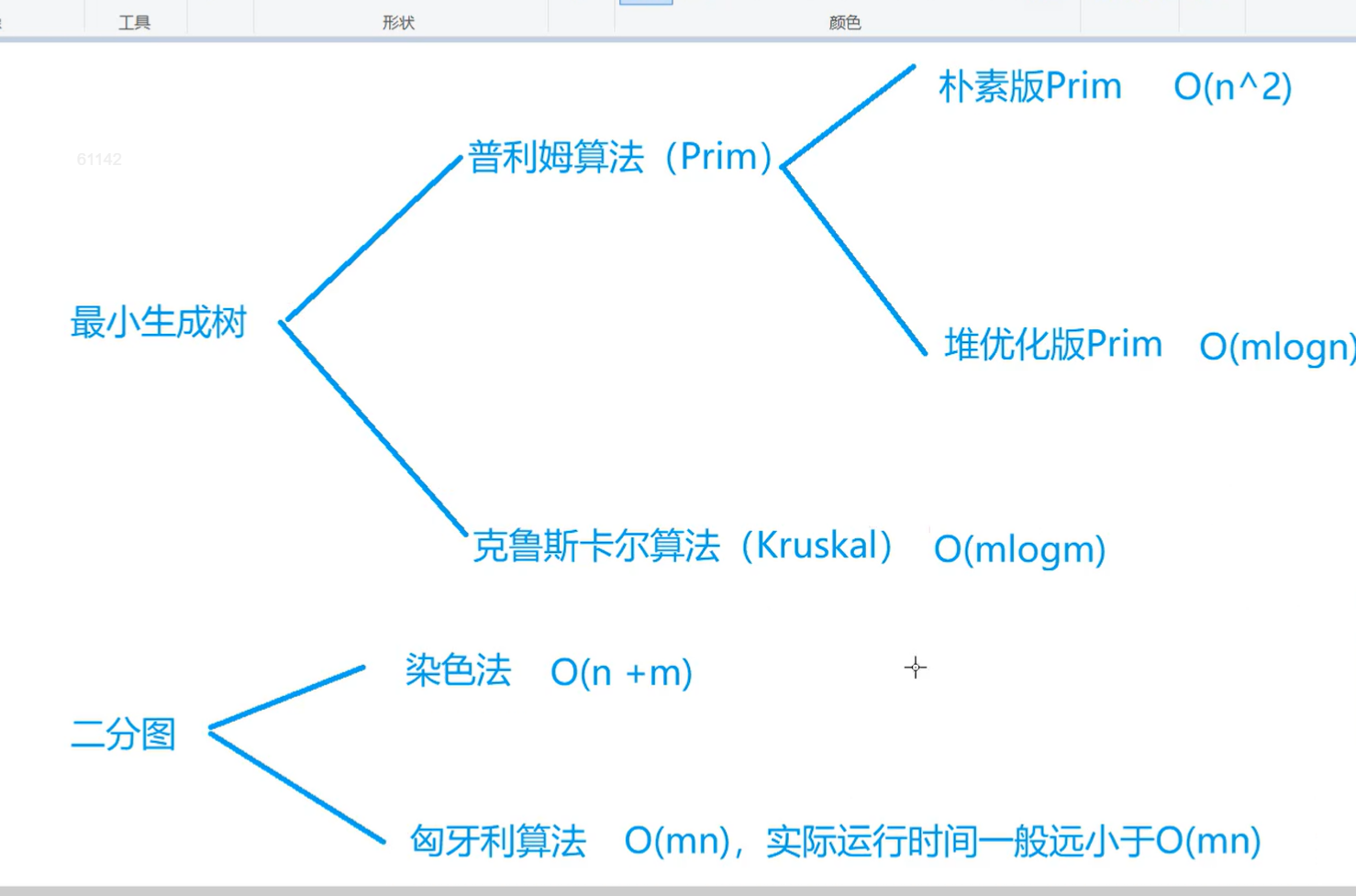

欧拉路径与欧拉回路:

传递闭包
for (int k = 0; k < n; ++k)
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
d[i][j] |= d[i][k] && d[k][j];
树的重心
数中包含n个节点,n-1条无向边,输出将重心删除后,剩余各个联通块中点数的最大值
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
#include <iostream>
#include <vector>
using namespace std;
const int N = 100010;
vector<int> g[N];
bool st[N];
int n, ans = N + 1;
int dfs(int u) {
st[u] = true;
int sum = 1, size = 0; // 包含当前节点的子树中点的数量,连通块中点的最大数量
for (int v : g[u]) {
if (!st[v]) {
int s = dfs(v);
sum += s;
size = max(size, s);
}
}
size = max(size, n - sum);
ans = min(ans, size);
return sum;
}
int main(void) {
scanf("%d", &n);
for (int i = 1; i < n; ++i) {
int a, b;
scanf("%d%d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
dfs(1);
cout << ans;
return 0;
}
最短路
dijkstra(朴素
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int g[N][N];
int dist[N];
bool st[N];
int n, m;
int dijkstra() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 1; i <= n; ++i) {
int t = -1;
for (int j = 1; j <= n; ++j)
if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
st[t] = true;
for (int j = 1; j <= n; ++j) dist[j] = min(dist[j], dist[t] + g[t][j]);
}
if (dist[n] == INF) return -1;
return dist[n];
}
int main(void) {
cin >> n >> m;
memset(g, 0x3f, sizeof g);
while (m--) {
int a, b, w;
cin >> a >> b >> w;
g[a][b] = min(g[a][b], w);
}
int ans = dijkstra();
cout << ans;
return 0;
}
dijkstra(堆优化
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
#include <iostream>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 150010, INF = 0x3f3f3f3f;
vector<PII> g[N];
int dist[N];
bool st[N];
int n, m;
int dijkstra() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while (heap.size()) {
int u = heap.top().second; heap.pop();
if (st[u]) continue;
st[u] = true;
for (PII t : g[u]) {
int v = t.first, w = t.second;
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
heap.push({dist[v], v});
}
}
}
if (dist[n] == INF) return -1;
return dist[n];
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
g[a].push_back({b, w});
}
int ans = dijkstra();
printf("%d", ans);
return 0;
}
bellmen-ford(有边数限制的最短路)
n个点,m条边,求1~n最多经过k条边的最短距离(可能存在负权回路,边权可能为负数,有向图
#include <iostream>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 510, M = 10010, INF = 0x3f3f3f3f;
struct Node {
int a, b, w;
} g[M];
int dist[N], backup[N];
int n, m, k;
int ford() {
memset(dist, INF, sizeof dist);
dist[1] = 0;
while (k--) {
memcpy(backup, dist, sizeof dist);
for (int i = 1; i <= m; ++i) {
int a = g[i].a, b = g[i].b, w = g[i].w;
dist[b] = min(dist[b], backup[a] + w);
}
}
if (dist[n] > INF / 2) return -1;
return dist[n];
}
int main(void) {
cin >> n >> m >> k;
for (int i = 1; i <= m; ++i)
cin >> g[i].a >> g[i].b >> g[i].w;
int ans = ford();
if (ans == -1) cout << "impossible";
else cout << ans;
return 0;
}
spfa(求最短路
n个点m条边的有向图,边权有负数,没有负权回路
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010, INF = 0x3f3f3f3f;
vector<PII> g[N];
int dist[N];
bool st[N];
int n, m;
int spfa() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size()) {
int u = q.front(); q.pop();
st[u] = false;
for (PII t : g[u]) {
int v = t.first, w = t.second;
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
if (!st[v]) {
st[v] = true;
q.push(v);
}
}
}
}
if (dist[n] == INF) return -1;
return dist[n];
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
g[a].push_back({b, w});
}
int ans = spfa();
if (ans == -1) puts("impossible");
else cout << ans;
return 0;
}
spfa判负环
有负环。
#include <iostream>
#include <queue>
#include <vector>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010, INF = 0x3f3f3f3f;
vector<PII> g[N];
int dist[N], cnt[N];
bool st[N];
int n, m;
bool spfa() {
queue<int> q;
for (int i = 1; i <= n; ++i) {
q.push(i);
st[i] = true;
}
while (q.size()) {
int u = q.front(); q.pop();
st[u] = false;
for (PII t : g[u]) {
int v = t.first, w = t.second;
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
cnt[v] = cnt[u] + 1;
if (cnt[v] > n) return true;
if (!st[v]) {
st[v] = true;
q.push(v);
}
}
}
}
return false;
}
int main(void) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a].push_back({b, c});
}
if (spfa()) puts("Yes");
else puts("No");
return 0;
}
Floyd多源最短路
有自环,边权可负
n个点m条有向边,给出k个询问,打印最短距离
#include <iostream>
#include <cstring>
using namespace std;
const int N = 210, INF = 0x3f3f3f3f;
int d[N][N];
int n, m, k;
void floyd() {
for (int k = 1; k <= n; ++k)
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main(void) {
cin >> n >> m >> k;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
if (i != j) d[i][j] = INF;
for (int i = 1; i <= m; ++i) {
int a, b, w;
cin >> a >> b >> w;
d[a][b] = min(d[a][b], w);
}
floyd();
while (k--) {
int a, b;
cin >> a >> b;
if (d[a][b] > INF / 2) cout << "impossible" << endl;
else cout << d[a][b] << endl;
}
return 0;
}
恰好经过k条边的最短路
void mul(int c[][N], int a[][N], int b[][N])
{
static int temp[N][N];
memset(temp, 0x3f, sizeof temp);
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
temp[i][j] = min(temp[i][j], a[i][k] + b[k][j]);
memcpy(c, temp, sizeof temp);
}
void qmi()
{
memset(res, 0x3f, sizeof res);
for (int i = 1; i <= n; i ++ ) res[i][i] = 0;
while (k)
{
if (k & 1) mul(res, res, g); // res = res * g
mul(g, g, g); // g = g * g
k >>= 1;
}
}
// 强制更新
int bellmanFord(){
memset(dis, 0x3f, sizeof dis);
dis[s] = 0;
for(register int i = 1; i <= n; i++){
memcpy(bDis, dis, sizeof dis);
memset(dis, 0x3f, sizeof dis);
for(register int j = 1; j <= m; j++){
dis[e[j].v] = min(dis[e[j].v], bDis[e[j].u] + e[j].w);
dis[e[j].u] = min(dis[e[j].u], bDis[e[j].v] + e[j].w);
}
}
return dis[t];
}
最小生成树
Prim
n个点,m条边的无向图。有重边和自环。边权可能为负
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int g[N][N];
int dist[N];
bool st[N];
int n, m;
int prim() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
int res = 0;
for (int i = 1; i <= n; ++i) {
int t = -1;
for (int j = 1; j <= n; ++j)
if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
if (dist[t] == INF) return INF;
res += dist[t];
st[t] = true;
for (int j = 1; j <= n; ++j) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
int main(void) {
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g);
while (m--) {
int a, b, w;
cin >> a >> b >> w;
g[a][b] = g[b][a] = min(g[a][b], w);
}
int t = prim();
if (t == INF) puts("impossible");
else cout << t;
return 0;
}
Kruskal
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010, M = 200010, INF = 0x3f3f3f3f;
struct Node {
int a, b, w;
bool operator<(const Node &t) const {
return w < t.w;
}
} g[M];
int n, m;
int p[N];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal() {
int res = 0, cnt = 0;
for (int i = 1; i <= m; ++i) {
int a = g[i].a, b = g[i].b, w = g[i].w;
a = find(a), b = find(b);
if (a != b) {
p[a] = b;
res += w;
cnt++;
}
}
if (cnt < n - 1) return INF;
return res;
}
int main(void) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
g[i].a = a, g[i].b = b, g[i].w = w;
}
sort(g + 1, g + m + 1);
for (int i = 1; i <= n; ++i) p[i] = i;
int t = kruskal();
if (t == INF) cout << "impossible";
else cout << t;
return 0;
}
二分图
染色法判定二分图
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环。
#include <iostream>
#include <vector>
using namespace std;
const int N = 100010, INF = 0x3f3f3f3f;
vector<int> g[N];
int color[N];
int n, m;
bool dfs(int u, int c) {
color[u] = c;
for (int v : g[u]) {
if (!color[v]) {
if (!dfs(v, 3 - c)) return false;
} else if (color[v] == c) return false;
}
return true;
}
int main(void) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int a, b;
scanf("%d%d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
bool flag = true;
for (int i = 1; i <= n; ++i) {
if (!color[i]) {
if (!dfs(i, 1)) {
flag = false;
break;
}
}
}
if (flag) puts("Yes");
else puts("No");
return 0;
}
二分图的最大匹配
给定一个二分图,其中左半部包含 n1 个点(编号 1∼n1),右半部包含 n2 个点(编号 1∼n2),二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。请你求出二分图的最大匹配数。
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int N = 510, M = 100010, INF = 0x3f3f3f3f;
vector<int> g[N];
int match[N];
bool st[N];
int n1, n2, m;
bool find(int u) {
for (int v : g[u]) {
if (!st[v]) {
st[v] = true;
if (match[v] == 0 || find(match[v])) {
match[v] = u;
return true;
}
}
}
return false;
}
int main(void) {
scanf("%d%d%d", &n1, &n2, &m);
for (int i = 1; i <= m; ++i) {
int a, b;
scanf("%d%d", &a, &b);
g[a].push_back(b);
}
int res = 0;
for (int i = 1; i <= n1; ++i) {
memset(st, 0, sizeof st);
if (find(i)) res++;
}
cout << res;
return 0;
}
最小路径重复点覆盖
#include <iostream>
#include <cstring>
using namespace std;
const int N = 210;
bool d[N][N], st[N];
int match[N];
int n, m;
bool find(int x) {
for (int i = 1; i <= n; ++i) {
if (!d[x][i] || st[i]) continue;
st[i] = true;
if (match[i] == 0 || find(match[i])) {
match[i] = x;
return true;
}
}
return false;
}
int main(void) {
cin >> n >> m;
while (m--) {
int a, b;
cin >> a >> b;
d[a][b] = true;
}
// 传递闭包
for (int k = 1; k <= n; ++k) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
d[i][j] |= d[i][k] && d[k][j];
}
}
}
int res = 0;
for (int i = 1; i <= n; ++i) {
memset(st, false, sizeof st);
if (find(i)) res++;
}
cout << n - res;
return 0;
}
欧拉回路
判断并打印回路(的边
/*
边的编号从1开始,点的编号1~n
type == 1 表示无向边,type == 2 表示有向边
n,m为点数和边数
存在欧拉回路打印YES,否则NO
打印欧拉回路的一路径
*/
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010, M = 2 * 200010;
int h[N], ne[M], e[M], idx;
bool used[M];
int ru[N], chu[N];
int ans[M], cnt;
int type, n, m;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
for (int &i = h[u]; ~i;) {
if (used[i]) {
i = ne[i];
continue;
}
used[i] = true;
if (type == 1) used[i ^ 1] = true;
int t;
if (type == 1) {
t = i / 2 + 1;
if (i & 1) t = -t;
} else t = i + 1;
int v = e[i];
i = ne[i];
dfs(v);
ans[++cnt] = t;
}
}
int main(void) {
scanf("%d%d%d", &type, &n, &m);
memset(h, -1, sizeof h);
for (int i = 1; i <= m; ++i) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
ru[b]++, chu[a]++;
if (type == 1) add(b, a);
}
if (type == 1) {
for (int i = 1; i <= n; ++i) {
if (ru[i] + chu[i] & 1) {
puts("NO");
return 0;
}
}
} else {
for (int i = 1; i <= n; ++i) {
if (ru[i] != chu[i]) {
puts("NO");
return 0;
}
}
}
for (int i = 1; i <= n; ++i) {
if (h[i] != -1) {
dfs(i);
break;
}
}
if (cnt < m) {
puts("NO");
return 0;
}
puts("YES");
for (int i = cnt; i; i--)
printf("%d ", ans[i]);
return 0;
}
字典序最小输出无向图的欧拉路径
/*
按字典序遍历即可
n个点(1~500),m个边,输出路径经过的顶点编号
*/
#include <iostream>
using namespace std;
const int N = 510, M = 1100;
int g[N][N];
int ans[M], cnt;
int du[N];
int n = 500, m;
void dfs(int u) {
for (int i = 1; i <= n; ++i) {
if (g[u][i]) {
g[u][i]--, g[i][u]--;
dfs(i);
}
}
ans[++cnt] = u;
}
int main(void) {
cin >> m;
while (m--) {
int a, b;
cin >>a >> b;
du[a]++, du[b]++;
g[a][b]++, g[b][a]++;
}
int start = 1;
while (!du[start]) start++;
for (int i = 1; i <= n; ++i) {
if (du[i] & 1) {
start = i;
break;
}
}
dfs(start);
for (int i = cnt; i; i--) cout << ans[i] <<endl;
return 0;
}
LCA
给定一棵包含 n 个节点的有根无向树,节点编号互不相同,但不一定是 1∼n。
有 m 个询问,每个询问给出了一对节点的编号 x 和 y,询问 x 与 y 的祖孙关系。
输入格式
输入第一行包括一个整数 表示节点个数;
接下来 n 行每行一对整数 a 和 b,表示 a 和 b 之间有一条无向边。如果 b 是 −1,那么 a 就是树的根;
第 n+2 行是一个整数 m 表示询问个数;
接下来 m 行,每行两个不同的正整数 x 和 y,表示一个询问。
输出格式
对于每一个询问,若 x 是 y 的祖先则输出 1,若 y 是 x 的祖先则输出 2,否则输出 0。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 40010, M = N * 2;
int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][16];
int q[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void bfs(int root)
{
memset(depth, 0x3f, sizeof depth);
depth[0] = 0, depth[root] = 1;
int hh = 0, tt = 0;
q[0] = root;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (depth[j] > depth[t] + 1)
{
depth[j] = depth[t] + 1;
q[ ++ tt] = j;
fa[j][0] = t;
for (int k = 1; k <= 15; k ++ )
fa[j][k] = fa[fa[j][k - 1]][k - 1];
}
}
}
}
int lca(int a, int b)
{
if (depth[a] < depth[b]) swap(a, b);
for (int k = 15; k >= 0; k -- )
if (depth[fa[a][k]] >= depth[b])
a = fa[a][k];
if (a == b) return a;
for (int k = 15; k >= 0; k -- )
if (fa[a][k] != fa[b][k])
{
a = fa[a][k];
b = fa[b][k];
}
return fa[a][0];
}
int main()
{
scanf("%d", &n);
int root = 0;
memset(h, -1, sizeof h);
for (int i = 0; i < n; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
if (b == -1) root = a;
else add(a, b), add(b, a);
}
bfs(root);
scanf("%d", &m);
while (m -- )
{
int a, b;
scanf("%d%d", &a, &b);
int p = lca(a, b);
if (p == a) puts("1");
else if (p == b) puts("2");
else puts("0");
}
return 0;
}
数论
质数
哥德巴赫猜想
哥德巴赫猜想的内容如下:
任意一个大于 4 的偶数都可以拆成两个奇素数之和。
例如:
8=3+5
20=3+17=7+13
42=5+37=11+31=13+29=19+23
现在,你的任务是验证所有小于一百万的偶数能否满足哥德巴赫猜想。
6≤n<106
#include <iostream>
using namespace std;
const int N = 1000010;
int prime[N], cnt;
bool st[N];
void init(int n) {
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++cnt] = i;
for (int j = 1; prime[j] <= n / i; ++j) {
st[prime[j] * i] = true;
if (i % prime[j] == 0) break;
}
}
}
int main(void) {
init(N - 1);
int n;
while (cin >> n, n) {
for (int i = 1; ; ++i) {
int x = prime[i], y = n - x;
if (!st[y]) {
printf("%d = %d + %d\n", n, x, y);
break;
}
}
}
return 0;
}
质数距离
给定两个整数 L 和 U,你需要在闭区间 [L,U] 内找到距离最接近的两个相邻质数 C1 和 C2(即 C2−C1 是最小的),如果存在相同距离的其他相邻质数对,则输出第一对。
同时,你还需要找到距离最远的两个相邻质数 D1 和 D2(即 D1−D2 是最大的),如果存在相同距离的其他相邻质数对,则输出第一对。
1≤L<U≤2^31−1
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 1000010;
int prime[N], cnt;
bool st[N];
int init(int n) {
memset(st, false, sizeof st);
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++cnt] = i;
for (int j = 1; prime[j] <= n / i; ++j) {
st[prime[j] * i] = true;
if (i % prime[j] == 0) break;
}
}
}
signed main(void) {
int l, r;
while (cin >> l >> r) {
init (50000);
memset(st, false, sizeof st);
for (int i = 1; i <= cnt; ++i) {
LL p = prime[i];
for (LL j = max(p * 2, (l + p - 1) / p * p); j <= r; j += p) {
st[j - l] = true;
}
}
cnt = 0;
for (int i = 0; i <= r - l; ++i) {
if (!st[i] && i + l >= 2)
prime[++cnt] = i + l;
}
if (cnt < 2) {
puts("There are no adjacent primes.");
continue;
}
int a = 1, b = 1;
for (int i = 1; i + 1 <= cnt; ++i) {
int d = prime[i + 1] - prime[i];
if (d < prime[a + 1] - prime[a]) a = i;
if (d > prime[b + 1] - prime[b]) b = i;
}
printf("%d,%d are closest, %d,%d are most distant.\n",
prime[a], prime[a + 1], prime[b], prime[b + 1]);
}
}
分解质因数
将n分解质因数,输出底数和指数
void solve() {
int n;
cin >> n;
for (int i = 2; i <= n / i; ++i) {
if (n % i == 0) {
int s = 0;
while (n % i == 0) n /= i, s++;
cout << i << ' ' << s << endl;
}
}
if (n > 1) cout << n << ' ' << 1 << endl;
}
阶乘分解
给定整数 N,试把阶乘 N! 分解质因数,按照算术基本定理的形式输出分解结果中的 pi 和 ci 即可。
#include <iostream>
using namespace std;
const int N = 1000010;
int prime[N], cnt;
bool st[N];
int n;
void init(int n)
{
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++cnt] = i;
for (int j = 1; prime[j] <= n / i; ++j) {
st[prime[j] * i] = true;
if (i % prime[j] == 0) break;
}
}
}
int main(void)
{
int n;
cin >> n;
init(n);
for (int i = 1; i <= cnt; ++i) {
int p = prime[i];
int s = 0;
for (int j = n; j; j /= p) {
s += j / p;
}
cout << p << ' ' << s <<endl;
}
return 0;
}
约数
约数个数
输入n个正整数,求他们成绩的约数个数
(s1+1)*(s2+1)*...*(sn+1)
#include <iostream>
#include <unordered_map>
using namespace std;
const int MOD = 1e9 + 7;
int main(void) {
int n;
cin >> n;
unordered_map<int, int> mp;
while (n--) {
int x;
cin >> x;
for (int i = 2; i <= x / i; ++i) {
if (x % i == 0) {
int s = 0;
while (x % i == 0) x /= i, s++;
mp[i] += s;
}
}
if (x > 1) mp[x] += 1;
}
//LL
int res = 1;
for (auto it : mp) {
int s = it.second;
res = (long long)res * (s + 1) % MOD;
}
cout << res;
return 0;
}
约数之和
输入n个数,求它们乘积的约数之和
(p^0+p^1+...+p^k)*()...*()
#include <iostream>
#include <unordered_map>
using namespace std;
const int MOD = 1e9 + 7;
typedef long long LL;
int main(void) {
int n;
cin >> n;
unordered_map<int, int> mp;
while (n--) {
int x;
cin >> x;
for (int i = 2; i <= x / i; ++i) {
if (x % i == 0) {
int s = 0;
while (x % i == 0) x /= i, s++;
mp[i] += s;
}
}
if (x > 1) mp[x] += 1;
}
int res = 1;
for (auto e : mp) {
int p = e.first, s = e.second;
int t = 1;
while (s--) {
t = ((LL)t * p + 1l) % MOD;
}
res = (LL) res * t % MOD;
}
cout << res;
return 0;
}
樱花
给定一个整数 n,求有多少正整数数对 (x,y) 满足 1/x+1/y=1/n!。
将式子转换,本质上让求(n!)^2的约数个数
1≤n≤10^6
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1000010, mod = 1e9 + 7;
int prime[N], cnt;
bool st[N];
void init(int n)
{
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++cnt] = i;
for (int j = 1; prime[j] <= n / i; ++j) {
st[prime[j] * i] = true;
if (i % prime[j] == 0) break;
}
}
}
int main(void)
{
int n;
cin >> n;
init(n);
int res = 1;
for (int i = 1; i <= cnt; ++i) {
int p = prime[i];
int s = 0;
for(int j = n; j; j /= p) s += j / p;
res = (LL) res * (2 * s + 1) % mod;
}
cout << res;
return 0;
}
反素数
对于任何正整数 x,其约数的个数记作 g(x),例如 g(1)=1、g(6)=4。
如果某个正整数 x 满足:对于任意的小于 x 的正整数 i,都有 g(x)>g(i),则称 x 为反素数。
例如,整数 1,2,4,6 等都是反素数。
现在给定一个数 N,请求出不超过 N 的最大的反素数。
1≤N≤2∗10^9
#include <iostream>
using namespace std;
int prime[9] = {2, 3, 5, 7, 11, 13, 17, 19, 23};
int maxv, number;
int n;
void dfs(int u, int last, int p, int s)
{
if (s > maxv || s == maxv && p < number) {
number = p;
maxv = s;
}
if (u == 9) return;
for (int i = 1; i <= last; ++i) {
if ((long long) p * prime[u] > n) break;
p *= prime[u];
dfs(u + 1, i, p, s * (i + 1));
}
}
int main(void)
{
cin >> n;
dfs(0, 30, 1, 1);
cout << number;
return 0;
}
欧拉
欧拉函数
1~n中与n互质的数的个数
void solve(int n) {
int res = n;
for (int i = 2; i <= n / i; ++i)
if (n % i == 0) {
res = res / i * (i - 1);
while (n % i == 0) n /= i;
}
if (n > 1) res = res / n * (n - 1);
cout << res << endl;
}
欧拉筛
const int N = 1000010;
int prime[N], cnt, phi[N];
bool st[N];
void get_phi(int n) {
phi[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!st[i]) {
prime[++cnt] = i;
phi[i] = i - 1;
}
for (int j = 1; prime[j] <= n / i; ++j) {
st[prime[j] * i] = true;
if (i % prime[j] == 0) {
phi[prime[j] * i] = prime[j] * phi[i];
break;
}
phi[prime[j] * i] = phi[i] * (prime[j] - 1);
}
}
}
扩展欧几里得
int exgcd(int a, int b, int &x, int &y) {
if (!b) {
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
组合数
组合数

输出C(b,a)
C(b,a) -> C[a][b]
void init() {
for (int i = 0; i < N; ++i)
for (int j = 0; j <= i; ++j)
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
}
组合数II
求C(b,a)%mod
给定a,b。输出C(b,a)
1<=b<=a<=1e5
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9 + 7;
int fact[N], infact[N];
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int main()
{
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
int n;
scanf("%d", &n);
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
return 0;
}
组合数III
求C(b,a)%mod
给定a,b,p,其中p是质数。输出C(b,a)%p
1<=n<=20, 1<=b<=a<=1e18, 1<=p<=1e5
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p)
{
if (b > a) return 0;
int res = 1;
for (int i = 1, j = a; i <= b; i ++, j -- )
{
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
LL a, b;
int p;
cin >> a >> b >> p;
cout << lucas(a, b, p) << endl;
}
return 0;
}
DP
最长上升子序列
#include <iostream>
using namespace std;
const int N = 100010;
int f[N], a[N];
int main(void) {
int n;
cin >> n;
for (int i = 0; i < n; ++i) cin >> a[i];
int len = 0;
for (int i = 0; i < n; ++i) {
int l = 0, r = len;
while (l < r) {
int mid = l + r + 1 >> 1;
if (f[mid] < a[i]) l = mid;
else r = mid - 1;
}
f[r + 1] = a[i];
len = max(r + 1, len);
}
cout << len << endl;;
//for (int i = 1; i <= n; ++i) cout << f[i] << ' ';
return 0;
}
最长公共子序列
小沐沐说,对于两个数列 A 和 B,如果它们都包含一段位置不一定连续的数,且数值是严格递增的,那么称这一段数是两个数列的公共上升子序列,而所有的公共上升子序列中最长的就是最长公共上升子序列了。
输出:
输出一个整数,表示最长公共上升子序列的长度。
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main(void) {
cin >> n >> m;
cin >> a + 1 >> b + 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
}
cout << f[n][m];
return 0;
}
最短编辑距离
给定两个字符串 A 和 B,现在要将 A 经过若干操作变为 B,可进行的操作有:
- 删除–将字符串 A 中的某个字符删除。
- 插入–在字符串 A 的某个位置插入某个字符。
- 替换–将字符串 A 中的某个字符替换为另一个字符。
求最少操作次数
#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N];
char a[N], b[N];
int main(void) {
int n, m;
cin >> n >> a + 1;
cin >> m >> b + 1;
for (int i = 0; i <= n; ++i) f[i][0] = i;
for (int i = 0; i <= m; ++i) f[0][i] = i;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
}
}
cout << f[n][m];
return 0;
}
整数划分
一个正整数 n 可以表示成若干个正整数之和,形如:n=n1+n2+…+nk,其中 n1≥n2≥…≥nk,k≥1。
我们将这样的一种表示称为正整数 n 的一种划分。
现在给定一个正整数 n,请你求出 n 共有多少种不同的划分方法。
背包写法:
#include <iostream>
using namespace std;
const int N = 1010, MOD = 1e9 + 7;
int f[N];
int main(void) {
int n;
cin >> n;
f[0] = 1;
for (int i = 1; i <= n; ++i)
for (int j = i; j <= n; ++j)
f[j] = (f[j] + f[j - i]) % MOD;
cout << f[n];
return 0;
}
其他算法
#include <iostream>
using namespace std;
const int N = 1010, MOD = 1e9 + 7;
int f[N][N];
int main(void) {
// f[i][j]表示总和为i,总个数为j的方案数
int n;
cin >> n;
f[1][1] = 1;
f[0][0] = 1;
for (int i = 2; i <= n; ++i)
for (int j = 1; j <= i; ++j)
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % MOD;
int res = 0;
for (int i = 0; i <= n; ++i) res = (res + f[n][i]) % MOD;
cout << res;
return 0;
}
数字三角形模型
最低费用
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110;
int f[N][N], w[N][N];
int main(void) {
int n;
cin >> n;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j)
cin >> w[i][j];
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (i == 1 && j == 1) f[i][j] = w[i][j];
else {
f[i][j] = 0x3f3f3f3f;
if (i > 1) f[i][j] = f[i - 1][j] + w[i][j];
if (j > 1) f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
}
}
}
cout << f[n][n];
return 0;
}
走两次的最大值
#include <iostream>
using namespace std;
const int N = 110;
int f[N+N][N][N], w[N][N];
int main(void) {
int n;
cin >> n;
int a, b, c;
while (cin >> a >> b >> c, a || b || c) w[a][b] = c;
for (int k = 2; k <= n + n; ++k) {
for (int i1 = 1; i1 <= n; ++i1) {
for (int i2 = 1; i2 <= n; ++i2) {
int j1 = k - i1, j2 = k - i2;
if (j1 < 1 || j1 > n || j2 < 1 || j2 > n) continue;
int t = w[i1][j1];
if (j1 != j2) t += w[i2][j2];
int &v = f[k][i1][i2];
v = max(v, f[k - 1][i1][i2] + t);
v = max(v, f[k - 1][i1 - 1][i2 - 1] + t);
v = max(v, f[k - 1][i1 - 1][i2] + t);
v = max(v, f[k - 1][i1][i2 - 1] + t);
}
}
}
cout << f[n + n][n][n];
return 0;
}
最长上升子序列模型
登山问题
先上去再下来,最多能浏览几个点呢?
#include <iostream>
using namespace std;
const int N = 1010;
int f[N], g[N], h[N];
int main(void) {
int n;
cin >> n;
for (int i = 1; i <= n; ++i) cin >> h[i];
for (int i = 1; i <= n; ++i) {
f[i] = 1;
for (int j = 1; j < i; ++j) {
if (h[j] < h[i]) f[i] = max(f[i], f[j] + 1);
}
}
for (int i = n; i; --i) {
g[i] = 1;
for (int j = n; j > i; --j) {
if (h[j] < h[i]) g[i] = max(g[i], g[j] + 1);
}
}
int res = 0;
for (int i = 1; i <= n; ++i) res = max(res, f[i] + g[i] - 1);
cout << res;
return 0;
}
友好城市
一条河道分割南北两边的城市,给出n组相连的南北城市的坐标,最多有几组路线互不相交的城市?
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5010;
struct Node {
int a, b;
bool operator< (const Node &t) const {
return a < t.a;
}
} c[N];
int f[N];
int main(void) {
int n;
cin >> n;
for (int i = 1; i <= n; ++i) cin >> c[i].a >> c[i].b;
sort(c + 1, c + n + 1);
int res = 0;
for (int i = 1; i <= n; ++i) {
f[i] = 1;
for (int j = 1; j < i; ++j) {
if (c[j].b < c[i].b) f[i] = max(f[i], f[j] + 1);
}
res = max(res, f[i]);
}
cout << res;
return 0;
}
最大上升子序列和
#include <iostream>
using namespace std;
const int N = 1010;
int f[N], w[N];
int main(void) {
int n;
cin >> n;
for (int i = 1; i <= n; ++i) cin >> w[i];
int res = 0;
for (int i = 1; i <= n; ++i) {
f[i] = w[i];
for (int j = 1; j < i; ++j) {
if (w[j] < w[i]) f[i] = max(f[i], f[j] + w[i]);
}
res = max(res, f[i]);
}
cout << res;
return 0;
}
覆盖整个区间的最少有序序列问题
能覆盖整个序列最少的不上升子序列个数 == 该序列的最长上升子序列长度
能覆盖整个序列最少的不下降子序列个数 == 该序列最长下降子序列长度
/*
求最长上升子序列最大长度
int cnt = 0;
for (int i = 0; i < n; ++i) {
int k = 0;
while (k < cnt && g[k] < w[i]) k++;
g[k] = w[i];
if (k >= cnt) cnt++;
}
cout << cnt;
*/
导弹防御系统
为了对抗附近恶意国家的威胁,R 国更新了他们的导弹防御系统。
一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。
例如,一套系统先后拦截了高度为 3 和高度为 4 的两发导弹,那么接下来该系统就只能拦截高度大于 4 的导弹。
给定即将袭来的一系列导弹的高度,请你求出至少需要多少套防御系统,就可以将它们全部击落。
#include <iostream>
using namespace std;
const int N = 55;
int w[N], up[N], down[N];
int ans, n;
void dfs(int u, int su, int sd) {
if (su + sd >= ans) return ;
if (u == n) {
ans = su + sd;
return ;
}
// up
int k = 0;
while (k < su && up[k] <= w[u]) k++;
int t = up[k];
up[k] = w[u];
if (k >= su) dfs(u + 1, su + 1, sd);
else dfs(u + 1, su, sd);
up[k] = t;
// down
k = 0;
while (k < sd && down[k] >= w[u]) k++;
t = down[k];
down[k] = w[u];
if (k >= sd) dfs(u + 1, su, sd + 1);
else dfs(u + 1, su, sd);
down[k] = t;
}
int main(void) {
while (cin >> n, n) {
for (int i = 0; i < n; ++i) cin >> w[i];
ans = n;
dfs(0, 0, 0);
cout << ans << endl;
}
return 0;
}
最长公共上升子序列
#include <iostream>
using namespace std;
const int N = 3010;
int f[N][N];
int a[N], b[N];
int main(void) {
int n;
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
for (int i = 1; i <= n; ++i) cin >> b[i];
for (int i = 1; i <= n; ++i) {
int t = 1;
for (int j = 1; j <= n; ++j) {
f[i][j] = f[i - 1][j];
if (a[i] == b[j]) f[i][j] = max(f[i][j], t);
if (b[j] < a[i]) t = max(t, f[i - 1][j] + 1);
}
}
int res = 0;
for (int i = 1; i <= n; ++i) res = max(res, f[n][i]);
cout << res;
return 0;
}
打印路径
#include "bits/stdc++.h"
using namespace std;
const int N = 1010;
struct Node
{
int a, b, id;
bool operator< (const Node &t) const
{
if (a != t.a) return a < t.a;
return b > t.b;
}
} mouse[N];
int pre[N], f[N];
void dfs(int k)
{
if (!k) return ;
dfs(pre[k]);
cout << mouse[k].id << endl;
}
int main(void)
{
int n = 0;
int a, b;
while (cin >> a >> b)
{
++n;
mouse[n].a = a, mouse[n].b = b, mouse[n].id = n;
}
sort(mouse + 1, mouse + n + 1);
int k = 1;
for (int i = 1; i <= n; ++i)
{
f[i] = 1;
for (int j = 1; j <= i; ++j)
{
if (mouse[i].a > mouse[j].a && mouse[i].b < mouse[j].b && f[i] < f[j] + 1)
{
f[i] = f[j] + 1;
pre[i] = j;
}
}
if (f[k] < f[i]) k = i;
}
cout << f[k] << endl;
dfs(k);
return 0;
}
背包模型
初始化总结

01背包求方案数
给定 N 个正整数 A1,A2,…,AN,从中选出若干个数,使它们的和为 M,求有多少种选择方案。
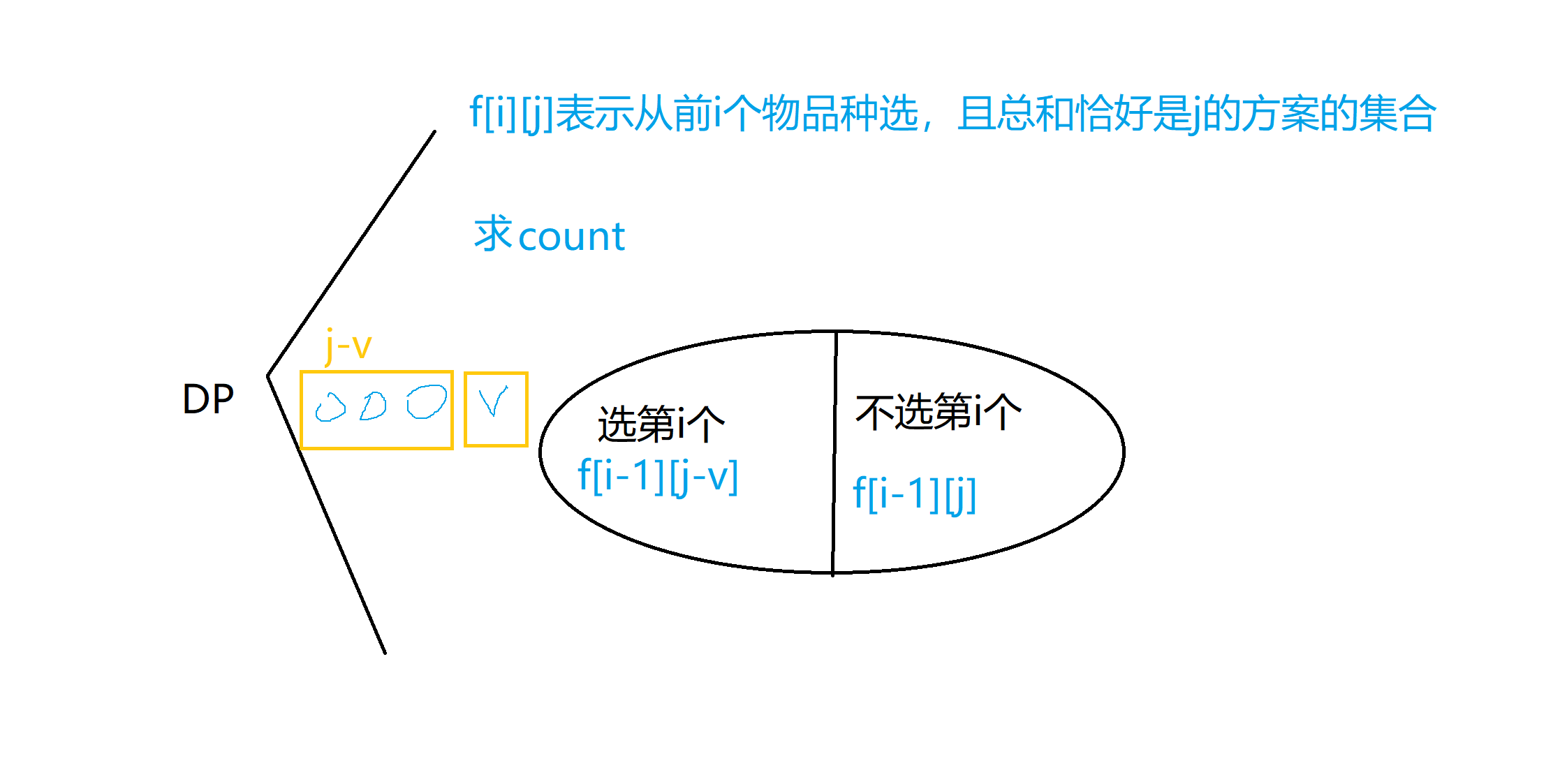
#include <iostream>
using namespace std;
const int N = 10010;
int f[N];
int main(void) {
int n, m;
cin >> n >> m;
f[0] = 1;
while (n--) {
int v;
cin >> v;
for (int i = m; i >= v; --i)
f[i] += f[i - v];
}
cout << f[m];
return 0;
}
完全背包求方案数
给你一个n种面值的货币系统,求组成面值为m的货币有多少种方案。
n≤15,m≤3000
#include <iostream>
using namespace std;
const int N = 3010;
long long f[N];
int main(void) {
int n, m;
cin >> n >> m;
f[0] = 1;
while (n--) {
int v;
cin >> v;
for (int i = v; i <= m; ++i) f[i] += f[i - v];
}
cout << f[m];
return 0;
}
多重背包
#include <iostream>
using namespace std;
const int N = 6010;
int f[N];
int main(void) {
int n, m;
cin >> n >> m;
while (n--) {
int v, w, s;
cin >> v >> w >> s;
for (int i = m; i >= 0; --i) {
for (int j = 0; j <= s && j * v <= i; ++j)
f[i] = max(f[i], f[i - j * v] + j * w);
}
}
cout << f[m];
return 0;
}
多重背包II
0<N≤1000
0<V≤2000
0<vi,wi,si≤2000
#include <iostream>
using namespace std;
const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[M];
int main(void) {
cin >> n >> m;
int cnt = 0;
for (int i = 1; i <= n; ++i) {
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while (k <= s) {
cnt++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k <<= 1;
}
if (s > 0) {
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for (int i = 1; i <= n; ++i)
for (int j = m; j >= v[i]; --j)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m];
return 0;
}
多重背包III
0<N≤1000
0<V≤20000
0<vi,wi,si≤20000
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20010;
int n, m;
int f[N], g[N], q[N];
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i ++ )
{
int v, w, s;
cin >> v >> w >> s;
memcpy(g, f, sizeof f);
for (int j = 0; j < v; j ++ )
{
int hh = 0, tt = -1;
for (int k = j; k <= m; k += v)
{
if (hh <= tt && q[hh] < k - s * v) hh ++ ;
while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt -- ;
q[ ++ tt] = k;
f[k] = g[q[hh]] + (k - q[hh]) / v * w;
}
}
}
cout << f[m] << endl;
return 0;
}
混合背包问题
加二进制优化
#include <iostream>
using namespace std;
const int N = 1010;
int f[N];
int main(void) {
int n, m;
cin >> n >> m;
while (n--) {
int v, w, s;
cin >> v >> w >> s;
if (s == 0) {
for (int i = v; i <= m; ++i) f[i] = max(f[i], f[i - v] + w);
} else {
if (s < 0) s = 1;
for (int k = 1; k <= s; k <<= 1) {
for (int i = m; i >= k * v; --i)
f[i] = max(f[i], f[i - k * v] + k * w);
s -= k;
}
if (s) {
for (int i = m; i >= s * v; --i)
f[i] = max(f[i], f[i - s * v] + s * w);
}
}
}
cout << f[m];
return 0;
}
价值最小问题
状态定义:f[i][j]为体积至多为[i][j]的最小价值
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110;
int f[N][N];
int main(void) {
int m1, m2, n;
cin >> m1 >> m2 >> n;
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
while (n--) {
int v1, v2, w;
cin >> v1 >> v2 >> w;
for (int i = m1; i >= 0; --i) {
for (int j = m2; j >= 0; --j) {
f[i][j] = min(f[i][j], f[max(0, i - v1)][max(0, j - v2)] + w);
}
}
}
cout << f[m1][m2];
return 0;
}
分组背包
#include <iostream>
using namespace std;
const int N = 110;
int f[N], v[N][N], w[N][N], s[N];
int main(void) {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
cin >> s[i];
for (int j = 1; j <= s[i]; ++j)
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; ++i) {
for (int j = m; j >= 0; --j) {
for (int k = 1; k <= s[i]; ++k)
if (j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
cout << f[m];
return 0;
}
分组背包求方案数
总公司拥有M台 相同 的高效设备,准备分给下属的N个分公司。
各分公司若获得这些设备,可以为国家提供一定的盈利。盈利与分配的设备数量有关。
问:如何分配这M台设备才能使国家得到的盈利最大?
求出最大盈利值。
分配原则:每个公司有权获得任意数目的设备,但总台数不超过设备数M。
输入格式
第一行有两个数,第一个数是分公司数N,第二个数是设备台数M;
接下来是一个N*M的矩阵,矩阵中的第 i 行第 j 列的整数表示第 i 个公司分配 j 台机器时的盈利。
输出格式
第一行输出最大盈利值;
接下N行,每行有2个数,即分公司编号和该分公司获得设备台数。
答案不唯一,输出任意合法方案即可。
#include <iostream>
using namespace std;
const int N = 20, M = 20;
int f[N][M], w[N][N], way[N];
int main(void) {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
for (int j = 1 ; j <= m; ++j)
cin >> w[i][j];
}
for (int i = 1; i <= n; ++i) {
for (int j = m; j >= 0; --j) {
f[i][j] = f[i - 1][j];
for (int k = 1; k <= j; ++k)
f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
}
}
int j = m;
for (int i = n; i; --i) {
for (int k = 0; k <= m; ++k) {
if (k <= j && f[i][j] == f[i - 1][j - k] + w[i][k]) {
way[i] = k;
j -= k;
break;
}
}
}
cout << f[n][m] << endl;
for (int i = 1; i <= n; ++i) cout << i << ' ' << way[i] << ' ' << endl;
}
有依赖的背包问题
(分组背包)
有 N 个物品和一个容量是 V 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
每件物品的编号是 i,体积是 vi,价值是 wi,依赖的父节点编号是 pi。物品的下标范围是 1…N。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
#include <iostream>
#include <vector>
using namespace std;
const int N = 110;
int f[N][N], v[N], w[N];
vector<int> g[N];
int n, m;
void dfs(int u) {
for (int ne : g[u]) { // 枚举物品
dfs(ne);
for (int i = m - v[u]; i >= 0; --i) { // 枚举体积,给w[u]留空间
for (int j = 0; j <= i; ++j) { // 枚举方案,方案为体积
f[u][i] = max(f[u][i], f[u][i - j] + f[ne][j]);
}
}
}
for (int i = m; i >= v[u]; --i) f[u][i] = f[u][i - v[u]] + w[u]; // 添加w[u]
for (int i = 0; i < v[u]; ++i) f[u][i] = 0; // 不符合情况为0
}
int main(void) {
cin >> n >> m;
int root = -1;
for (int i = 1; i <= n; ++i) {
int a, b, p;
cin >> v[i] >> w[i] >> p;
if (p == -1) root = i;
else g[p].push_back(i);
}
dfs(root);
cout << f[root][m];
return 0;
}
求最优方案数
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 109+7 的结果。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010, MOD = 1e9 + 7;
int f[N], g[N];
int main(void) {
int n, m;
cin >> n >> m;
memset(f, -0x3f, sizeof f);
f[0] = 0; // 体积恰好为j的最大价值
g[0] = 1;
while (n--) {
int v, w;
cin >> v >> w;
for (int i = m; i >= v; --i) {
int val = max(f[i], f[i - v] + w);
int cnt = 0;
if (val == f[i]) cnt = g[i];
if (val == f[i - v] + w) cnt = (cnt + g[i - v]) % MOD;
g[i] = cnt;
f[i] = val;
}
}
int res = 0;
for (int i = 0; i <= m; ++i) res = max(res, f[i]);
int cnt = 0;
for (int i = 0; i <= m; ++i) {
if (res == f[i]) cnt = (cnt + g[i]) % MOD;
}
cout << cnt;
return 0;
}
求具体方案
字典序最小
#include <iostream>
using namespace std;
const int N = 1010;
int f[N][N], v[N], w[N];
int main(void) {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
for (int i = n; i >= 1; --i) {
for (int j = 0; j <= m; ++j) {
f[i][j] = f[i + 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
}
}
int j = m;
for (int i = 1; i <= n; ++i) {
if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) {
cout << i << ' ';
j -= v[i];
}
}
return 0;
}
状态机模型
不能选择两个连续的
你是一名盗贼,现在有n家店铺,你不能连续的偷两个店铺,问最多能偷盗多少钱
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int w[N], f[N][2];
void solve() {
//f[0][0] = 0, f[0][1] = -0x3f3f3f3f;
int n;
cin >> n;
for (int i = 1; i <= n; ++i) cin >> w[i];
for (int i = 1; i <= n; ++i) {
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + w[i];
}
cout << max(f[n][0], f[n][1]) << endl;
}
int main(void) {
int T;
cin >> T;
while (T--)
solve();
return 0;
}
股票买卖IV
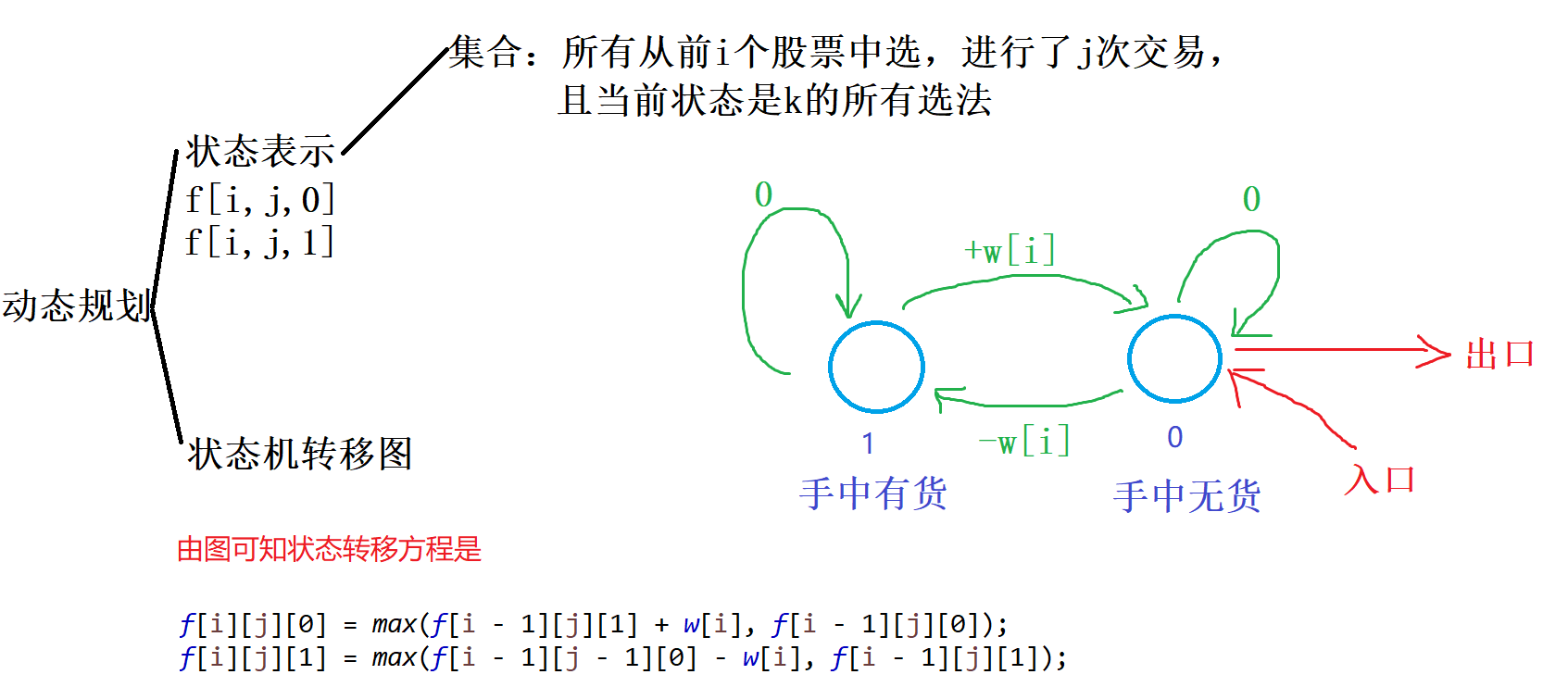
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润,你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010, K = 110;
int f[N][K][2], w[N]; // 在前i个股票中,第j个交易时,手中无货0,有货1
int main(void) {
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
memset(f, -0x3f, sizeof f);
for (int i = 0; i <= n; ++i) f[i][0][0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= k; ++j) {
f[i][j][1] = max(f[i - 1][j - 1][0] - w[i], f[i - 1][j][1]);
f[i][j][0] = max(f[i - 1][j][1] + w[i], f[i - 1][j][0]);
}
}
int res = 0;
for (int i = 0; i <= k; ++i) res = max(res, f[n][i][0]);
cout << res;
return 0;
}
股票买卖V
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
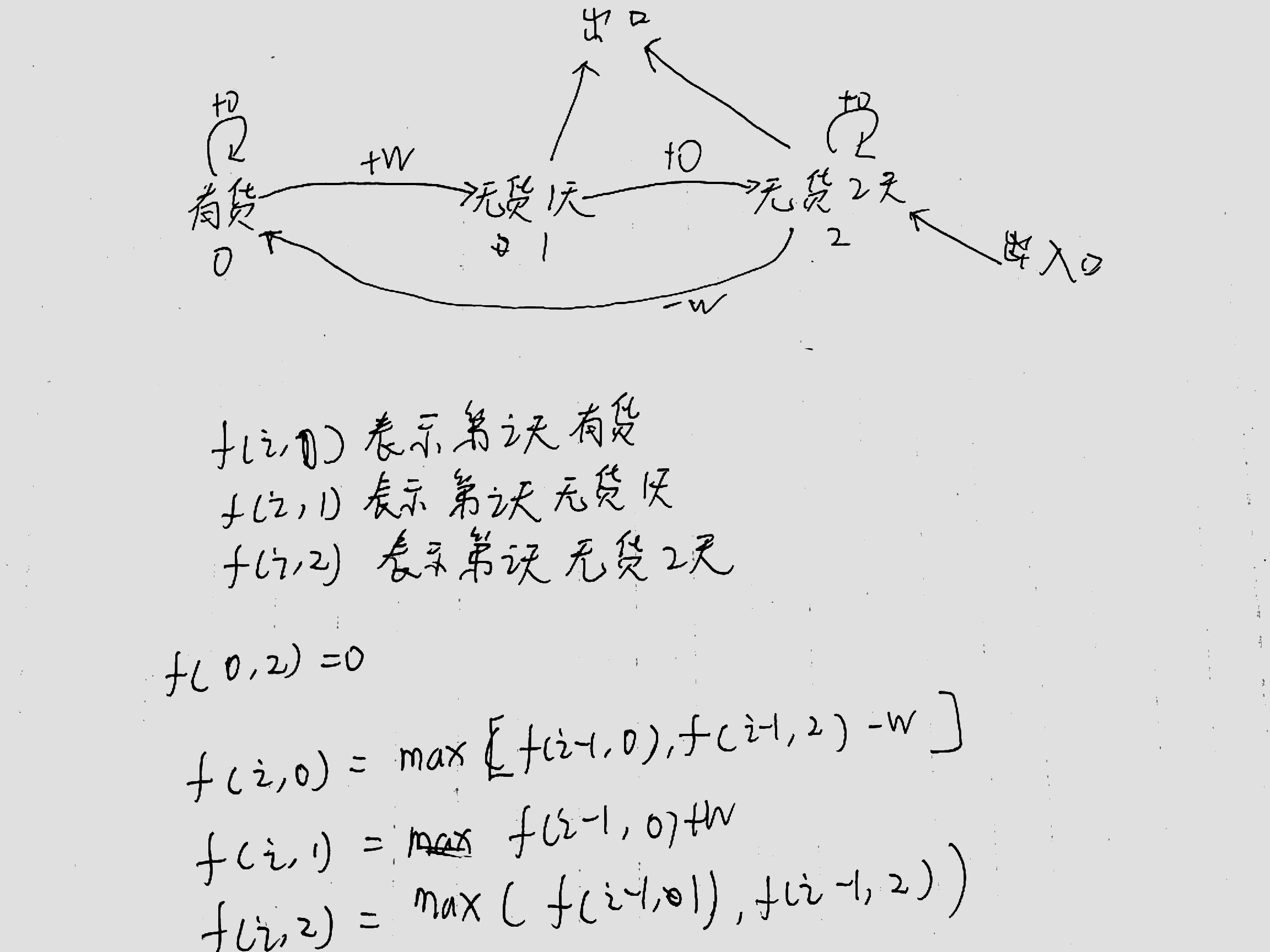
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010;
int f[N][3], w[N];
int main(void) {
int n;
cin >> n;
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
memset(f, -0x3f, sizeof f);
f[0][1] = f[0][2] = 0;
for (int i = 1; i <= n; ++i) {
f[i][0] = max(f[i - 1][0], f[i - 1][2] - w[i]);
f[i][1] = max(f[i - 1][1], f[i - 1][0] + w[i]);
f[i][2] = max(f[i - 1][1], f[i - 1][2]);
}
cout << max(f[n][1], f[n][2]);
return 0;
}
状态压缩模型
小国王
在 n×n 的棋盘上放 k 个国王,国王可攻击相邻的 8 个格子,求使它们无法互相攻击的方案总数。
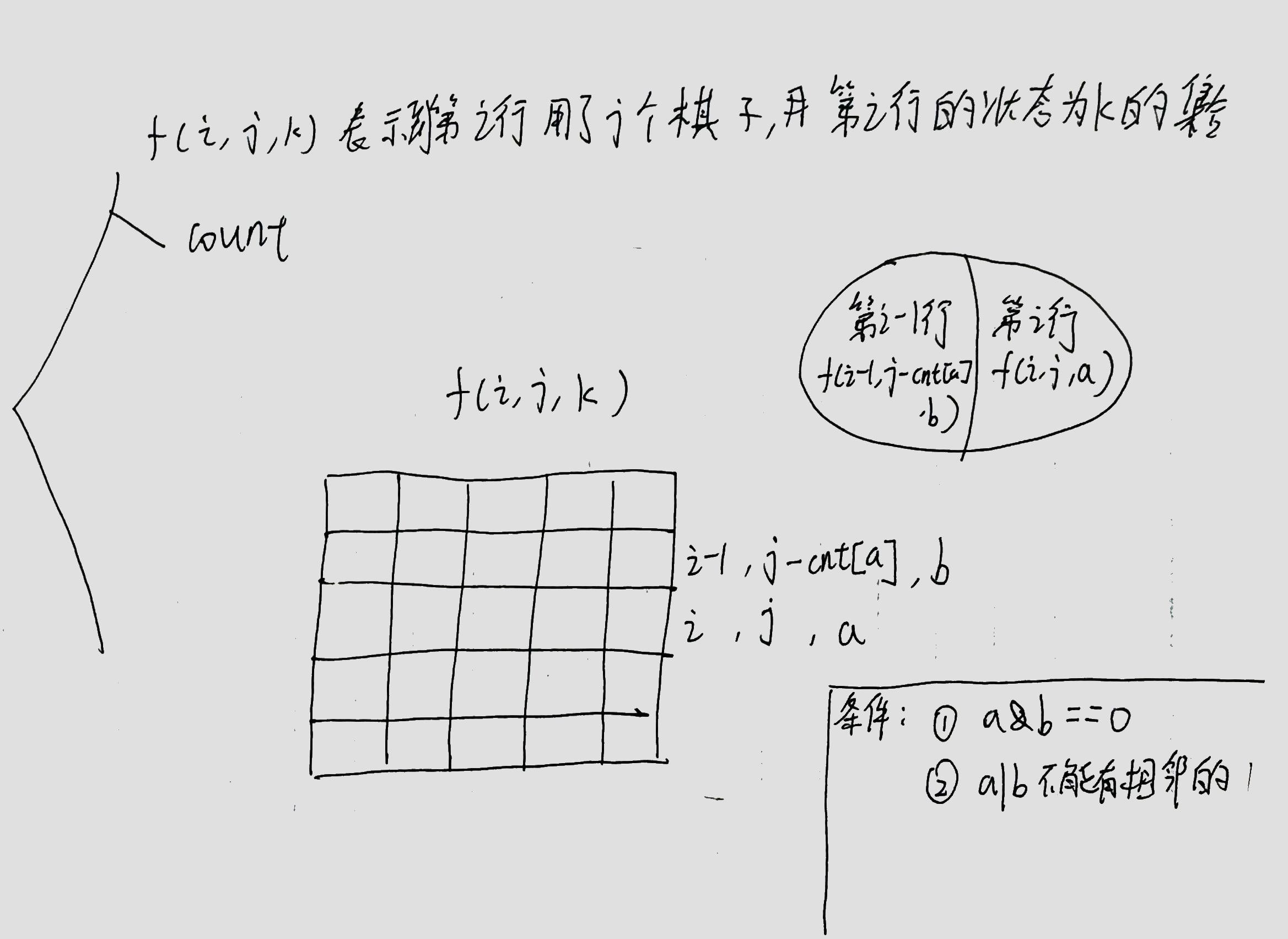
#include <iostream>
#include <vector>
using namespace std;
const int N = 15, M = 1 << 10, K = 120;
long long f[N][K][M];
vector<int> state;
vector<int> head[M]; // 可由状态i转移到状态j
int cnt[M]; // 存储状态i有多少个1
int n, k;
bool check(int x) {
for (int i = 0; i < n; ++i) {
if (x >> i & 1 && x >> i + 1 & 1) return false;
}
return true;
}
int count(int x) {
int res = 0;
for (int i = 0; i < n; ++i) res += x >> i & 1;
return res;
}
int main(void) {
cin >> n >> k;
for (int i = 0; i < 1 << n; ++i) {
if (check(i)) {
state.push_back(i);
cnt[i] = count(i);
}
}
for (int i = 0; i < state.size(); ++i) {
for (int j = 0; j < state.size(); ++j) {
int a = state[i], b = state[j];
if ((a & b) == 0 && check(a | b)) head[i].push_back(j); // 无向的
}
}
f[0][0][0] = 1;
for (int i = 1; i <= n + 1; ++i) {
for (int j = 0; j <= k; ++j) {
for (int a = 0; a < state.size(); ++a) {
for (int b : head[a]) {
int c = cnt[state[a]];
if (j >= c) f[i][j][a] += f[i-1][j-c][b];
}
}
}
}
cout << f[n + 1][k][0];
return 0;
}
玉米田
农夫约翰的土地由 M×N 个小方格组成,现在他要在土地里种植玉米。
非常遗憾,部分土地是不育的,无法种植。
而且,相邻的土地不能同时种植玉米,也就是说种植玉米的所有方格之间都不会有公共边缘。
现在给定土地的大小,请你求出共有多少种种植方法。
土地上什么都不种也算一种方法。
#include <iostream>
#include <vector>
using namespace std;
const int N = 13, M = 1 << N, MOD = 1e8;
int f[N][M]; // 第i行的状态为j
int w[M]; // 第i行的状态,1表示不育,
vector<int> state;
vector<int> g[M];
int n, m;
bool check(int x) {
for (int i = 0; i < m; ++i)
if (x >> i & 1 && x >> i + 1 & 1) return false;
return true;
}
int main(void) {
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < m; ++j) {
int x;
cin >> x;
w[i] = w[i] * 2 + !x;
}
}
for (int i = 0; i < 1 << m; ++i) {
if (check(i)) state.push_back(i);
}
for (int i = 0; i < state.size(); ++i) {
for (int j = 0; j < state.size(); ++j) {
int a = state[i], b = state[j];
if ((a & b) == 0) g[j].push_back(i);
}
}
f[0][0] = 1;
for (int i = 1; i <= n + 1; ++i) {
for (int a = 0; a < state.size(); ++a) {
for (int b : g[a]) {
if ((state[a] & w[i]) == 0 && (state[b] & w[i - 1]) == 0) {
f[i][a] = (f[i][a] + f[i - 1][b]) % MOD;
}
}
}
}
cout << f[n + 1][0];
return 0;
}
炮兵阵地
*
*
**X**
*
*
若在x处放置炮车,*区域均不能放置
给定一张n*m的图,图中H点固定不能放大炮
在n*m的网络中,最多可以放多少个大炮?
#include <iostream>
#include <vector>
using namespace std;
const int N = 110, M = 1 << 11;
long long f[2][M][M]; // 第i行,第i行的状态,第i-1行的状态
int w[N]; // 第i行的状态,1表示不能放大炮
vector<int> state;
vector<int> g[M];
int cnt[M];
int n, m;
bool check(int x) {
for (int i = 0; i < m; ++i) {
if (x >> i & 1 && (x >> i + 1 & 1 || x >> i + 2 & 1)) return false;
}
return true;
}
int count(int x) {
int res = 0;
for (int i = 0; i < m; ++i) res += x >> i & 1;
return res;
}
int main(void) {
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
string s;
cin >> s;
for (int j = 0; j < m; ++j) {
char ch = s[j];
int t = ch == 'H';
w[i] = w[i] * 2 + t;
}
}
for (int i = 0; i < 1 << m; ++i) {
if (check(i)) {
state.push_back(i);
cnt[i] = count(i);
}
}
for (int i = 1; i <= n; ++i) {
for (int u = 0; u < state.size(); ++u) { // i
for (int v = 0; v < state.size(); ++v) { // i - 1
for (int k = 0; k < state.size(); ++k) { // i - 2
int a = state[u], b = state[v], c = state[k];
if (a & b | a & c | b & c) continue;
if (w[i] & a | w[i - 1] & b) continue;
//if (i >= 2 && w[i - 2] & c) continue;
f[i & 1][u][v] = max(f[i & 1][u][v], f[i - 1 & 1][v][k] + cnt[a]);
}
}
}
}
long long res = 0;
for (int i = 0; i < state.size(); ++i) {
for (int j = 0; j < state.size(); ++j)
res = max(res, f[n & 1][i][j]);
}
cout << res;
return 0;
}
区间问题
环形石子合并
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
选择一种合并石子的方案,使得做 n−1 次合并得分总和最大。
选择一种合并石子的方案,使得做 n−1 次合并得分总和最小。
#include <iostream>
using namespace std;
const int N = 210;
int f[N][N], g[N][N];
int w[N], s[N];
int n;
int main(void) {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> w[i];
for (int i = n + 1; i <= n + n; ++i) w[i] = w[i - n];
for (int i = 1; i <= n + n; ++i) s[i] = s[i - 1] + w[i];
for (int len = 1; len <= n; ++len) {
for (int l = 1; l + len - 1 <= n + n; ++l) {
int r = l + len - 1;
if (l == r) continue;
f[l][r] = 2e9, g[l][r] = -2e9;
for (int k = l; k < r; ++k) {
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
}
}
}
int minv = 2e9, maxv = -2e9;
for (int i = 1; i <= n; ++i) {
minv = min(minv, f[i][i + n - 1]);
maxv = max(maxv, g[i][i + n - 1]);
}
cout << minv << endl << maxv;
return 0;
}
加分二叉树
设一个 n 个节点的二叉树 tree 的中序遍历为(1,2,3,…,n),其中数字 1,2,3,…,n 为节点编号。
每个节点都有一个分数(均为正整数),记第 i 个节点的分数为 di,tree 及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数
若某个子树为空,规定其加分为 1。
叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树 tree。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
#include <iostream>
using namespace std;
const int N = 35;
int w[N], f[N][N], g[N][N];
int n;
void dfs(int l, int r) {
if (l > r) return ;
cout << g[l][r] << ' ';
int k = g[l][r];
dfs(l, k - 1);
dfs(k + 1, r);
}
int main(void) {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> w[i];
for (int len = 1; len <= n; ++len) {
for (int i = 1; i + len - 1 <= n; ++i) {
int j = i + len - 1;
if (i == j) f[i][j] = w[i], g[i][j] = i;
else {
f[i][j] = -2e9;
for (int k = i; k <= j; ++k) {
int left = i == k ? 1 : f[i][k - 1];
int right = j == k ? 1 : f[k + 1][j];
int t = left * right + w[k];
if (f[i][j] < t) {
f[i][j] = t;
g[i][j] = k;
}
}
}
}
}
cout << f[1][n] << endl;
dfs(1, n);
return 0;
}
树形DP
树的最长路径
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
1≤n≤10000,
1≤ai,bi≤n,
−105≤ci≤105
#include <iostream>
#include <vector>
using namespace std;
const int N = 10010;
vector<pair<int, int>> g[N];
int n, ans;
int dfs(int u, int fa) {
int d1 = 0, d2 = 0, dist = 0;
for (auto t : g[u]) {
int v = t.first, val = t.second;
if (v == fa) continue;
int d = dfs(v, u) + val;
if (d > d1) d2 = d1, d1 = d;
else if (d > d2) d2 = d;
dist = max(dist, d);
}
ans = max(ans, d1 + d2);
return dist;
}
int main(void) {
cin >> n;
for (int i = 1; i < n; ++i) {
int a, b, c;
cin >> a >> b >> c;
g[a].push_back({b, c});
g[b].push_back({a, c});
}
dfs(1, -1);
cout << ans;
return 0;
}
树的中心
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
1≤n≤10000,
1≤ai,bi≤n,
1≤ci≤105
#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 10010, INF = 0x3f3f3f3f;
vector<PII> g[N];
int d1[N], d2[N], up[N], p1[N], p2[N];
int n;
int dfs_down(int u, int fa) {
d1[u] = d2[u] = -INF;
for (PII t : g[u]) {
int v = t.first, val = t.second;
if (v == fa) continue;
int d = dfs_down(v, u) + val;
if (d > d1[u]) {
d2[u] = d1[u], d1[u] = d;
p2[u] = p1[u], p1[u] = v;
} else if (d > d2[u]) {
d2[u] = d;
p2[u] = v;
}
}
if (d1[u] == -INF) d1[u] = d2[u] = 0;
return d1[u];
}
void dfs_up(int u, int fa) {
for (PII t : g[u]) {
int v = t.first, val = t.second;
if (v == fa) continue;
if (p1[u] == v) up[v] = max(up[u], d2[u]) + val;
else up[v] = max(up[u], d1[u]) + val;
dfs_up(v, u);
}
}
int main(void) {
cin >> n;
for (int i = 1; i < n; ++i) {
int a, b, c;
cin >> a >> b >> c;
g[a].push_back({b, c});
g[b].push_back({a, c});
}
dfs_down(1, -1);
dfs_up(1, -1);
int res = INF;
for (int i = 1; i <= n; ++i) res = min(res, max(up[i], d1[i]));
cout << res;
return 0;
}
数字转换
如果一个数 x 的约数之和 y(不包括他本身)比他本身小,那么 x 可以变成 y,y 也可以变成 x。
例如,4 可以变为 3,1 可以变为 7。
限定所有数字变换在不超过 n 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
1≤n≤50000
#include <iostream>
#include <vector>
using namespace std;
const int N = 50010;
vector<int> g[N];
int sum[N];
int n, ans;
int dfs(int u, int fa) {
int d1 = 0, d2 = 0;
for (int v : g[u]) {
if (v == fa) continue;
int d = dfs(v, u) + 1;
if (d > d1) d2 = d1, d1 = d;
else if (d > d2) d2 = d;
}
ans = max(ans, d1 + d2);
return d1;
}
int main(void) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
for (int j = 2; j <= n / i; ++j) {
sum[i * j] += i; // sum存储x的约数和(不包括x本身)
}
}
for (int i = 1; i <= n; ++i) {
if (sum[i] < i) {
g[sum[i]].push_back(i);
g[i].push_back(sum[i]);
}
}
dfs(1, -1);
cout << ans;
return 0;
}
二叉苹果树
有一棵二叉苹果树,如果树枝有分叉,一定是分两叉,即没有只有一个儿子的节点。
这棵树共 N 个节点,编号为 1 至 N,树根编号一定为 1。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。
一棵苹果树的树枝太多了,需要剪枝。但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留住多少苹果。
这里的保留是指最终与1号点连通。
#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int f[N][N]; // 以i为子树,选j条边的最大价值
vector<PII> g[N];
int n, m;
void dfs(int u, int fa) {
for (PII t : g[u]) {
int v = t.first, val = t.second;
if (v == fa) continue;
dfs(v, u);
for (int i = m; i >= 0; --i) {
for (int k = 0; k < i; ++k) {
f[u][i] = max(f[u][i], f[u][i - k - 1] + f[v][k] + val);
}
}
}
}
int main(void) {
cin >> n >> m;
for (int i = 1; i < n; ++i) {
int a, b, c;
cin >> a >> b >> c;
g[a].push_back({b, c});
g[b].push_back({a, c});
}
dfs(1, -1);
cout << f[1][m];
return 0;
}
贪心
区间选点
给定 N 个闭区间 [a,b],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。输出选择的点的最小数量。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
vector<PII> segs;
int main(void) {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int l, r;
scanf("%d%d", &l, &r);
segs.push_back({r, l});
}
sort(segs.begin(), segs.end());
int res = 0;
int t = -2e9;
for (auto it : segs) {
int l = it.second, r = it.first;
if (t < l) {
t = r;
res++;
}
}
cout << res;
return 0;
}
最大不相交区间数量
给定 N 个闭区间 [a,b],请你在数轴上选择若干区间,使得选中的区间之间互不相交(包括端点)。输出可选取区间的最大数量。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
vector<PII> segs;
int main(void) {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int l, r;
scanf("%d%d", &l, &r);
segs.push_back({r, l});
}
sort(segs.begin(), segs.end());
int res = 0;
int t = -2e9;
for (auto it : segs) {
int l = it.second, r = it.first;
if (t < l) {
t = r;
res++;
}
}
cout << res;
return 0;
}
区间分组
给定 N 个闭区间 [a,b],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
#define l first
#define r second
using namespace std;
typedef pair<int, int> PII;
int main(void) {
int n;
scanf("%d", &n);
vector<PII> segs;
for (int i = 1; i <= n; ++i) {
int l ,r;
scanf("%d%d", &l, &r);
segs.push_back({l, r});
}
sort(segs.begin(), segs.end());
priority_queue<int, vector<int>, greater<int>> heap;
for (PII t : segs) {
if (heap.size() == 0 || heap.top() >= t.l) heap.push(t.r);
else {
heap.pop();
heap.push(t.r);
}
}
cout << heap.size();
return 0;
}
区间覆盖
给定 N 个闭区间 [ai,bi]以及一个线段区间 [s,t],请你选择尽量少的区间,将指定线段区间完全覆盖。
输出最少区间数,如果无法完全覆盖则输出 −1。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
struct Node {
int l, r;
bool operator< (const Node &t) const {
return l < t.l;
}
} segs[N];
int main(void) {
int st, ed;
scanf("%d%d", &st, &ed);
int n;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &segs[i].l, &segs[i].r);
}
sort(segs + 1, segs + n + 1);
int flag = false;
int res = 0;
for (int i = 1; i <= n; ++i) {
int j = i, r = -2e9;
while (j <= n && segs[j].l <= st) {
r = max(r, segs[j].r);
j++;
}
if (r < st) break;
res++;
if (r >= ed) {
flag = true;
break;
}
st = r;
i = j - 1;
}
if (!flag) res = -1;
cout << res;
return 0;
}
Huffman树
#include <iostream>
#include <queue>
using namespace std;
int main(void) {
priority_queue<int, vector<int>, greater<int>> heap;
int n;
cin >> n;
while (n--) {
int x;
cin >> x;
heap.push(x);
}
int sum = 0;
while (heap.size() > 1) {
int a = heap.top(); heap.pop();
int b = heap.top(); heap.pop();
sum += a + b;
heap.push(a + b);
}
cout << sum;
return 0;
}
搜索
最短路模型
迷宫问题
其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
#include <iostream>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 1010;
int g[N][N];
bool st[N][N];
PII path[N][N];
int n;
void bfs(int x, int y) {
queue<PII> q;
q.push({x, y});
st[x][y] = true;
int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
while (q.size()) {
PII t = q.front(); q.pop();
int x = t.first, y = t.second;
for (int i = 0; i < 4; ++i) {
int a = x + dx[i], b = y + dy[i];
if (a >= 0 && a < n && b >= 0 && b < n && g[a][b] == 0 && !st[a][b]) {
st[a][b] = true;
path[a][b] = {x, y};
q.push({a, b});
}
}
}
}
int main(void) {
cin >> n;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> g[i][j];
}
}
bfs(n - 1, n - 1);
int x = 0, y = 0;
while (true) {
cout << x << ' ' << y << endl;
if (x == n - 1 && y == n - 1) break;
PII t = path[x][y];
x = t.first, y = t.second;
}
return 0;
}
双向广搜
字符串变换
已知有两个字串 A, B 及一组字串变换的规则(至多 6 个规则):
A1→B1
A2→B2
若在 10 步(包含 10 步)以内能将 A 变换为 B ,则输出最少的变换步数;否则输出 NO ANSWER!。
#include <iostream>
#include <unordered_map>
#include <queue>
using namespace std;
string a[10], b[10];
int n;
int extend(queue<string> &qa, queue<string> &qb, unordered_map<string, int> &da, unordered_map<string, int> &db, string a[], string b[]) {
for (int k = 0, sk = qa.size(); k < sk; ++k) {
string t = qa.front(); qa.pop();
for (int i = 0; i < t.size(); ++i) {
for (int j = 0; j < n; ++j) {
if (t.substr(i, a[j].size()) == a[j]) {
string state = t.substr(0, i) + b[j] + t.substr(i + a[j].size());
if (da.count(state)) continue;
if (db.count(state)) return da[t] + 1 + db[state];
da[state] = da[t] + 1;
qa.push(state);
}
}
}
}
return 11;
}
int bfs(string st, string ed) {
queue<string> qa, qb;
unordered_map<string, int> da, db;
qa.push(st), da[st] = 0;
qb.push(ed), db[ed] = 0;
while (qa.size() && qb.size()) {
int t;
if (qa.size() <= qb.size()) t = extend(qa, qb, da, db, a, b);
else t = extend(qb, qa, db, da, b, a);
if (t <= 10) return t;
}
return 11;
}
int main(void) {
string st, ed;
cin >> st >> ed;
while (cin >> a[n] >> b[n]) n++;
int t = bfs(st, ed);
if (t > 10) cout << "NO ANSWER!";
else cout << t;
return 0;
}
剪枝
数独
数独是一种传统益智游戏,你需要把一个 9×9 的数独补充完整,使得图中每行、每列、每个 3×3 的九宫格内数字 1∼9 均恰好出现一次。
请编写一个程序填写数独。
#include <iostream>
using namespace std;
const int N = 9, M = 1 << 9;;
int row[N], col[N], cell[N][N];
int ones[M], mp[M];
string str;
void init() {
for (int i = 0; i < N; ++i) row[i] = col[i] = (1 << N) - 1;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j)
cell[i][j] = (1 << N) - 1;
}
}
void draw(int x, int y, int t, bool is_set) {
if (is_set) str[x * N + y] = '1' + t;
else str[x * N + y] = '.';
int v = 1 << t;
if (!is_set) v = -v;
row[x] -= v;
col[y] -= v;
cell[x / 3][y / 3] -= v;
}
int get(int x, int y) {
return row[x] & col[y] & cell[x / 3][y / 3];
}
int lowbit(int x) {
return x & -x;
}
bool dfs(int cnt) {
if (!cnt) return true;
int minv = 10, x, y;
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (str[i * N + j] == '.') {
int state = get(i, j);
if (ones[state] < minv) {
minv = ones[state];
x = i, y = j;
}
}
}
}
int state = get(x, y);
for (int i = state; i; i -= lowbit(i)) {
int t = mp[lowbit(i)];
draw(x, y, t, true);
if (dfs(cnt - 1)) return true;
draw(x, y, t, false);
}
return false;
}
int main(void) {
for (int i = 0; i < N; ++i) mp[1 << i] = i;
for (int i = 0; i < 1 << N; ++i) {
for (int j = 0; j < N; ++j)
ones[i] += i >> j & 1;
}
while (cin >> str, str[0] != 'e') {
init();
int cnt = 0;
for (int i = 0, k = 0; i < N; ++i) {
for (int j = 0; j < N; ++j, ++k) {
if (str[k] != '.') {
int t = str[k] - '1';
draw(i, j, t, true);
} else cnt++;
}
}
dfs(cnt);
cout << str << endl;
}
return 0;
}
木棒
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 50 个长度单位。
然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。
请你设计一个程序,帮助乔治计算木棒的可能最小长度。
每一节木棍的长度都用大于零的整数表示。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n, w[N];
int length, sum;
bool st[N];
bool dfs(int u, int cur, int start) { // 当前组,当前组长度,枚举位置
if (u * length == sum) return true;
if (cur == length) return dfs(u + 1, 0, 0);
for (int i = start; i < n; ++i) {
if (st[i] || cur + w[i] > length) continue;
st[i] = true;
if (dfs(u, cur + w[i], i + 1)) return true;
st[i] = false;
if (!cur || cur + w[i] == length) return false;
int j = i;
while (j < n && w[j] == w[i]) j++;
i = j - 1;
}
return false;
}
int main(void) {
while (cin >> n, n) {
memset(st, false, sizeof st);
sum = 0;
for (int i = 0; i < n; ++i) cin >> w[i], sum += w[i];
sort(w, w + n);
reverse(w, w + n);
length = 1;
while (1) {
if (sum % length == 0 && dfs(0, 0, 0)) {
cout << length << endl;
break;
}
length++;
}
}
return 0;
}
迭代加深
加成序列
满足如下条件的序列 X(序列中元素被标号为 1、2、3…m)被称为“加成序列”:
X[1]=1
X[m]=n
X[1]<X[2]<…<X[m−1]<X[m]
对于每个 k(2≤k≤m)都存在两个整数 i 和 j (1≤i,j≤k−1,i 和 j 可相等),使得 X[k]=X[i]+X[j]。
你的任务是:给定一个整数 n,找出符合上述条件的长度 m 最小的“加成序列”。
如果有多个满足要求的答案,只需要找出任意一个可行解。
#include <iostream>
using namespace std;
const int N = 110;
int path[N];
int n;
bool dfs(int u, int k) {
if (u == k) return path[u - 1] == n;
bool st[N] = {0};
st[1] = true;
for (int i = u - 1; i >= 0; --i) {
for (int j = i; j >= 0; --j) {
int s = path[i] + path[j];
if (s > n || st[s] || s <= path[u - 1]) continue;
st[s] = true;
path[u] = s;
if (dfs(u + 1, k)) return true;
}
}
return false;
}
int main(void) {
path[0] = 1;
while (cin >> n, n) {
int k = 1;
while (!dfs(1, k)) k++;
for (int i = 0; i < k; ++i) cout << path[i] << ' ';
cout << endl;
}
return 0;
}
双向DFS
送礼物
达达帮翰翰给女生送礼物,翰翰一共准备了 N 个礼物,其中第 i 个礼物的重量是 G[i]。
达达的力气很大,他一次可以搬动重量之和不超过 W 的任意多个物品。
达达希望一次搬掉尽量重的一些物品,请你告诉达达在他的力气范围内一次性能搬动的最大重量是多少。
1≤N≤46,
1≤W,G[i]≤231−1
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 55;
int w[N];
int weight[1 << 25], cnt;
int n, m, ans, k;
void dfs1(int u, int s) {
if (u == k) {
weight[cnt++] = s;
return ;
}
dfs1(u + 1, s);
if ((LL) w[u] + s <= m) dfs1(u + 1, s + w[u]);
}
void dfs2(int u, int s) {
if (u == n) {
int l = 0, r = cnt - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if ((LL) weight[mid] + s <= m) l = mid;
else r = mid - 1;
}
ans = max(ans, weight[r] + s);
return ;
}
dfs2(u + 1, s);
if ((LL) w[u] + s <= m) dfs2(u + 1, s + w[u]);
}
int main(void) {
cin >> m >> n;
for (int i = 0; i < n; ++i) cin >> w[i];
sort(w, w + n);
reverse(w , w + n);
k = n / 2 + 2;
dfs1(0, 0);
sort(weight, weight + cnt);
cnt = unique(weight, weight + cnt) - weight;
dfs2(k, 0);
cout << ans;
return 0;
}
IDA*
排书
给定 n 本书,编号为 1∼n。
在初始状态下,书是任意排列的。
在每一次操作中,可以抽取其中连续的一段,再把这段插入到其他某个位置。
我们的目标状态是把书按照 1∼n 的顺序依次排列。
求最少需要多少次操作。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 22;
int n, q[N];
int w[5][N];
int f() {
int tot = 0;
for (int i = 0; i + 1 < n; ++i) {
if (q[i + 1] != q[i] + 1) tot++;
}
return (tot + 2) / 3;
}
bool dfs(int u, int depth) { // 当前深度,最大深度
if (u + f() > depth) return false;
if (f() == 0) return true;
for (int len = 1; len <= n; ++len) {
for (int i = 0; i + len - 1 < n; ++i) {
int j = i + len - 1;
for (int k = j + 1; k < n; ++k) {
memcpy(w[u], q, sizeof q);
int x, y;
for (x = j + 1, y = i; x <= k; ++x, ++y) q[y] = w[u][x];
for (x = i; x <= j; ++x, ++y) q[y] = w[u][x];
if (dfs(u + 1, depth)) return true;
memcpy(q, w[u], sizeof q);
}
}
}
return false;
}
int main(void) {
int T;
cin >> T;
while (T--) {
cin >> n;
for (int i = 0; i < n; ++i) cin >> q[i];
int depth = 0;
while (depth < 5 && !dfs(0, depth)) depth++;
if (depth >= 5) puts("5 or more");
else cout << depth << endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号