图论算法的一些模板

图论

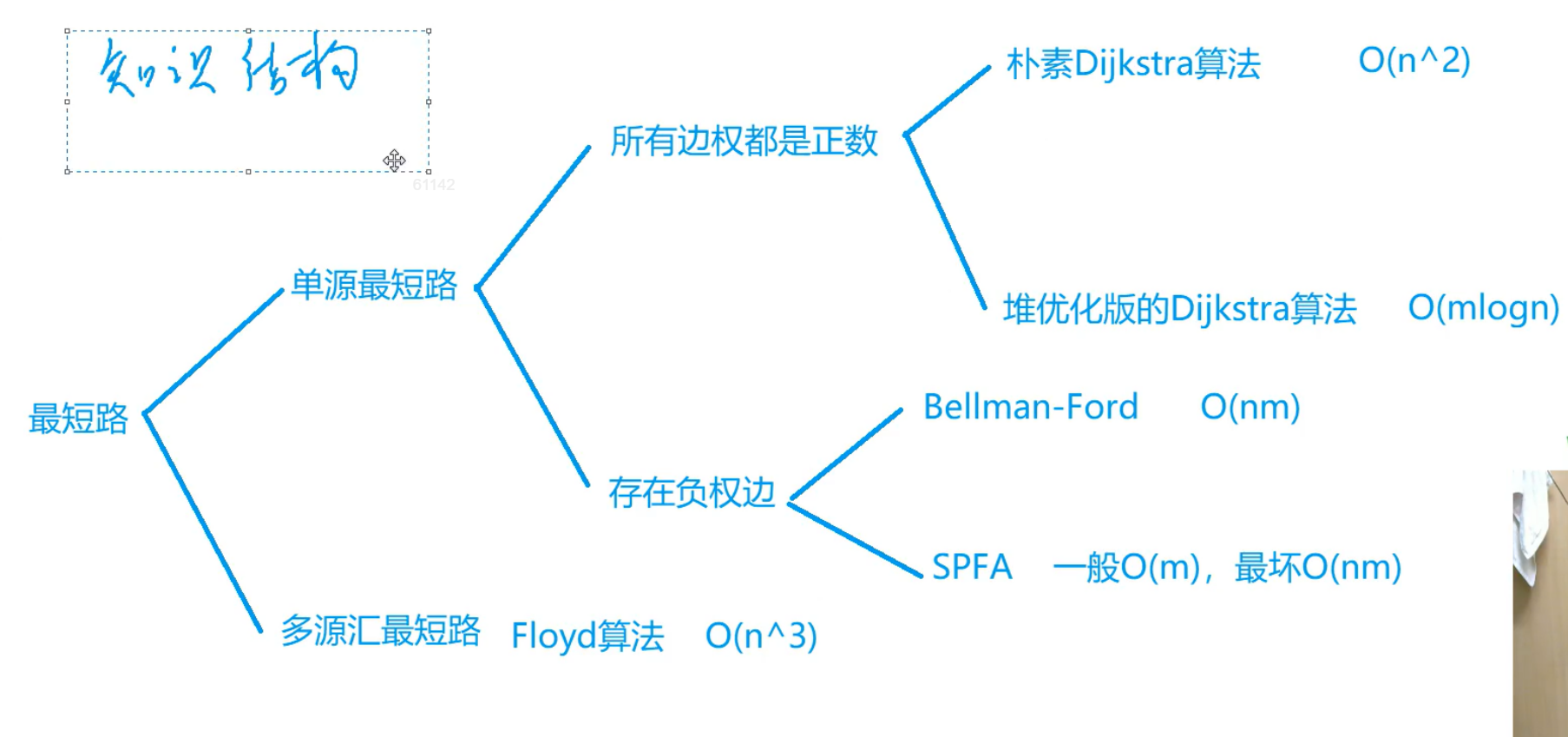
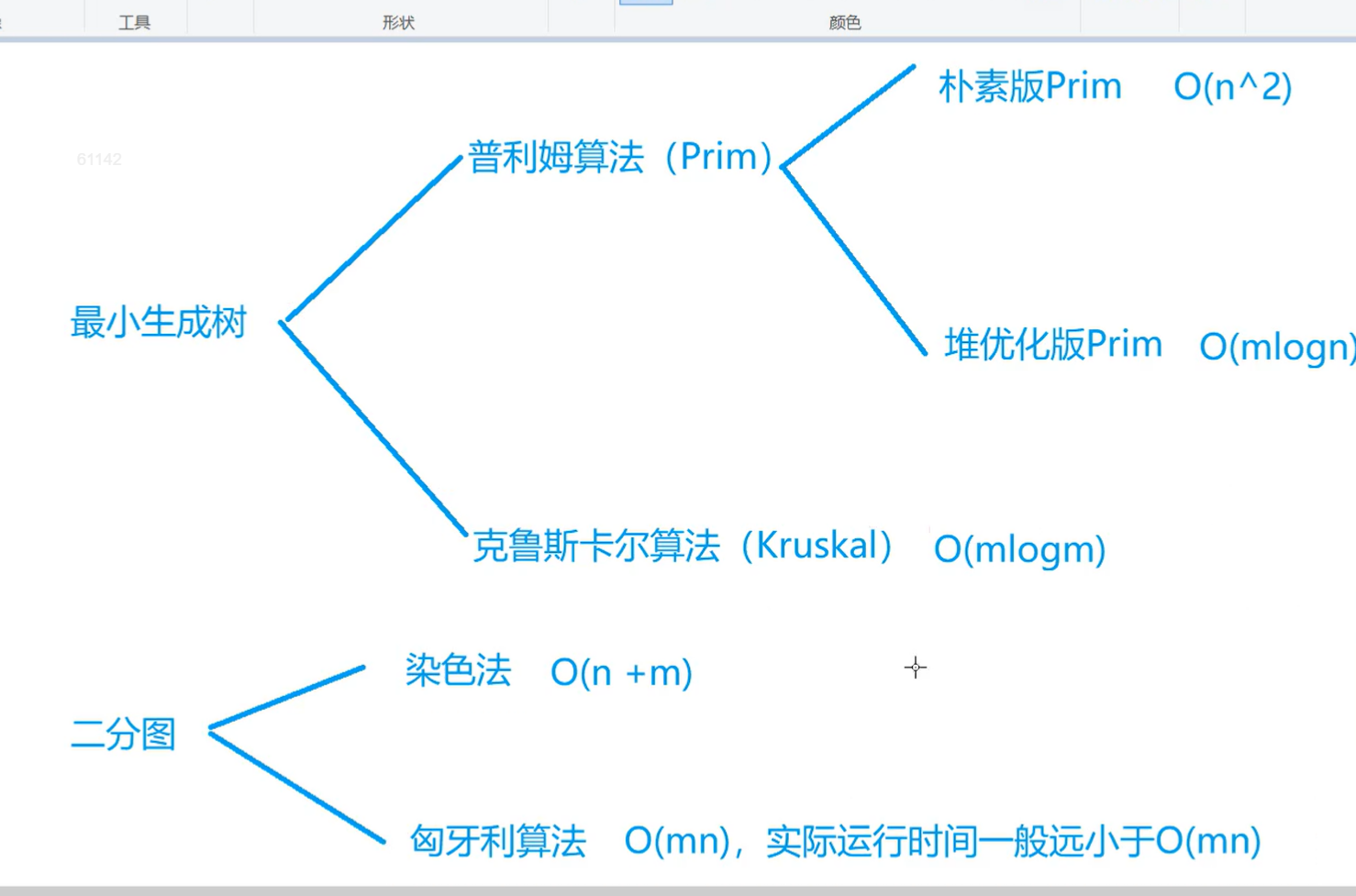
知识结构

欧拉路径与欧拉回路：

传递闭包

for (int k = 0; k < n; ++k)
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < n; ++j)
            d[i][j] |= d[i][k] && d[k][j];

树的重心

数中包含n个节点，n-1条无向边，输出将重心删除后，剩余各个联通块中点数的最大值

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

#include <iostream>
#include <vector>

using namespace std;

const int N = 100010;

vector<int> g[N];
bool st[N];
int n, ans = N + 1;

int dfs(int u) {
    st[u] = true;

    int sum = 1, size = 0; // 包含当前节点的子树中点的数量，连通块中点的最大数量
    for (int v : g[u]) {
        if (!st[v]) {
            int s = dfs(v);
            sum += s;
            size = max(size, s);
        }
    }

    size = max(size, n - sum);
    ans = min(ans, size);
    return sum;
}

int main(void) {
    scanf("%d", &n);

    for (int i = 1; i < n; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        g[a].push_back(b);
        g[b].push_back(a);
    }

    dfs(1);
    cout << ans;

    return 0;
}

最短路

dijkstra（朴素

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int g[N][N];
int dist[N];
bool st[N];
int n, m;

int dijkstra() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 1; i <= n; ++i) {
        int t = -1;
        for (int j = 1; j <= n; ++j)
            if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;

        st[t] = true;
        for (int j = 1; j <= n; ++j) dist[j] = min(dist[j], dist[t] + g[t][j]);
    }

    if (dist[n] == INF) return -1;
    return dist[n];
}

int main(void) {
    cin >> n >> m;

    memset(g, 0x3f, sizeof g);
    while (m--) {
        int a, b, w;
        cin >> a >> b >> w;
        g[a][b] = min(g[a][b], w);
    }

    int ans = dijkstra();
    cout << ans;

    return 0;
}

dijkstra（堆优化

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

#include <iostream>
#include <cstring>
#include <queue>
#include <vector>

using namespace std;

typedef pair<int, int> PII;

const int N = 150010, INF = 0x3f3f3f3f;

vector<PII> g[N];
int dist[N];
bool st[N];
int n, m;

int dijkstra() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});

    while (heap.size()) {
        int u = heap.top().second; heap.pop();

        if (st[u]) continue;
        st[u] = true;

        for (PII t : g[u]) {
            int v = t.first, w = t.second;
            if (dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
                heap.push({dist[v], v});
            }
        }
    }

    if (dist[n] == INF) return -1;
    return dist[n];
}

int main(void) {
    scanf("%d%d", &n, &m);
    while (m--) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        g[a].push_back({b, w});
    }

    int ans = dijkstra();
    printf("%d", ans);

    return 0;
}

bellmen-ford(有边数限制的最短路)

n个点，m条边，求1~n最多经过k条边的最短距离（可能存在负权回路，边权可能为负数，有向图

#include <iostream>
#include <cstring>

using namespace std;

typedef pair<int, int> PII;

const int N = 510, M = 10010, INF = 0x3f3f3f3f;


struct Node {
    int a, b, w;
} g[M];

int dist[N], backup[N];
int n, m, k;

int ford() {
    memset(dist, INF, sizeof dist);
    dist[1] = 0;

    while (k--) {
        memcpy(backup, dist, sizeof dist);
        for (int i = 1; i <= m; ++i) {
            int a = g[i].a, b = g[i].b, w = g[i].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }

    if (dist[n] > INF / 2) return -1;
    return dist[n];
}

int main(void) {
    cin >> n >> m >> k;

    for (int i = 1; i <= m; ++i)
        cin >> g[i].a >> g[i].b >> g[i].w;

    int ans = ford();

    if (ans == -1) cout << "impossible";
    else cout << ans;

    return 0;
}

spfa（求最短路

n个点m条边的有向图，边权有负数，没有负权回路

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>

using namespace std;

typedef pair<int, int> PII;

const int N = 100010, INF = 0x3f3f3f3f;

vector<PII> g[N];
int dist[N];
bool st[N];
int n, m;

int spfa() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    queue<int> q;
    q.push(1);
    st[1] = true;

    while (q.size()) {
        int u = q.front(); q.pop();

        st[u] = false;

        for (PII t : g[u]) {
            int v = t.first, w = t.second;
            if (dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
                if (!st[v]) {
                    st[v] = true;
                    q.push(v);
                }
            }
        }
    }

    if (dist[n] == INF) return -1;
    return dist[n];
}

int main(void) {
    scanf("%d%d", &n, &m);
    while (m--) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        g[a].push_back({b, w});
    }

    int ans = spfa();
    if (ans == -1) puts("impossible");
    else cout << ans;

    return 0;
}

spfa判负环

有负环。

#include <iostream>
#include <queue>
#include <vector>
#include <cstring>

using namespace std;

typedef pair<int, int> PII;

const int N = 100010, INF = 0x3f3f3f3f;

vector<PII> g[N];
int dist[N], cnt[N];
bool st[N];
int n, m;

bool spfa() {
    queue<int> q;
    for (int i = 1; i <= n; ++i) {
        q.push(i);
        st[i] = true;
    }

    while (q.size()) {
        int u = q.front(); q.pop();

        st[u] = false;

        for (PII t : g[u]) {
            int v = t.first, w = t.second;
            if (dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
                cnt[v] = cnt[u] + 1;
                if (cnt[v] > n) return true;

                if (!st[v]) {
                    st[v] = true;
                    q.push(v);
                }
            }
        }
    }

    return false;
}

int main(void) {
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= m; ++i) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a].push_back({b, c});
    }

    if (spfa()) puts("Yes");
    else puts("No");

    return 0;
}

Floyd多源最短路

有自环，边权可负

n个点m条有向边，给出k个询问，打印最短距离

#include <iostream>
#include <cstring>

using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int d[N][N];
int n, m, k;

void floyd() {

    for (int k = 1; k <= n; ++k)
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= n; ++j)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main(void) {
    cin >> n >> m >> k;

    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            if (i != j) d[i][j] = INF;

    for (int i = 1; i <= m; ++i) {
        int a, b, w;
        cin >> a >> b >> w;
        d[a][b] = min(d[a][b], w);
    }

    floyd();

    while (k--) {
        int a, b;
        cin >> a >> b;
        if (d[a][b] > INF / 2) cout << "impossible" << endl;
        else cout << d[a][b] << endl;
    }

    return 0;
}

恰好经过k条边的最短路

void mul(int c[][N], int a[][N], int b[][N])
{
    static int temp[N][N];
    memset(temp, 0x3f, sizeof temp);
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                temp[i][j] = min(temp[i][j], a[i][k] + b[k][j]);
    memcpy(c, temp, sizeof temp);
}

void qmi()
{
    memset(res, 0x3f, sizeof res);
    for (int i = 1; i <= n; i ++ ) res[i][i] = 0;

    while (k)
    {
        if (k & 1) mul(res, res, g);    // res = res * g
        mul(g, g, g);   // g = g * g
        k >>= 1;
    }
}

// 强制更新
int bellmanFord(){
    memset(dis, 0x3f, sizeof dis);
    dis[s] = 0;
    for(register int i = 1; i <= n; i++){
        memcpy(bDis, dis, sizeof dis);
        memset(dis, 0x3f, sizeof dis);
        for(register int j = 1; j <= m; j++){
            dis[e[j].v] = min(dis[e[j].v], bDis[e[j].u] + e[j].w);
            dis[e[j].u] = min(dis[e[j].u], bDis[e[j].v] + e[j].w);
        }
    }
    return dis[t];
}

最小生成树

Prim

n个点，m条边的无向图。有重边和自环。边权可能为负

#include <iostream>
#include <cstring>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int g[N][N];
int dist[N];
bool st[N];
int n, m;

int prim() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    int res = 0;
    for (int i = 1; i <= n; ++i) {
        int t = -1;
        for (int j = 1; j <= n; ++j)
            if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;

        if (dist[t] == INF) return INF;
        res += dist[t];
        st[t] = true;

        for (int j = 1; j <= n; ++j) dist[j] = min(dist[j], g[t][j]);
    }
    return res;
}

int main(void) {
    scanf("%d%d", &n, &m);

    memset(g, 0x3f, sizeof g);

    while (m--) {
        int a, b, w;
        cin >> a >> b >> w;
        g[a][b] = g[b][a] = min(g[a][b], w);
    }

    int t = prim();
    if (t == INF) puts("impossible");
    else cout << t;
    
    return 0;
}

Kruskal

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

struct Node {
    int a, b, w;
    bool operator<(const Node &t) const {
        return w < t.w;
    }
} g[M];

int n, m;
int p[N];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal() {
    int res = 0, cnt = 0;
    for (int i = 1; i <= m; ++i) {
        int a = g[i].a, b = g[i].b, w = g[i].w;
        a = find(a), b = find(b);
        if (a != b) {
            p[a] = b;
            res += w;
            cnt++;
        }
    }
    if (cnt < n - 1) return INF;
    return res;
}

int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; ++i) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        g[i].a = a, g[i].b = b, g[i].w = w;
    }
    
    sort(g + 1, g + m + 1);
    for (int i = 1; i <= n; ++i) p[i] = i;
    
    int t = kruskal();
    if (t == INF) cout << "impossible"; 
    else cout << t;
    
    return 0;
}

二分图

染色法判定二分图

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环。

#include <iostream>
#include <vector>

using namespace std;

const int N = 100010, INF = 0x3f3f3f3f;

vector<int> g[N];
int color[N];
int n, m;

bool dfs(int u, int c) {
    color[u] = c;
    for (int v : g[u]) {
        if (!color[v]) { 
            if (!dfs(v, 3 - c)) return false; 
        } else if (color[v] == c) return false;
    }
    return true;
}

int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        g[a].push_back(b);
        g[b].push_back(a);
    }
    
    bool flag = true;
    for (int i = 1; i <= n; ++i) {
        if (!color[i]) {
            if (!dfs(i, 1)) {
                flag = false;
                break;
            }
        }
    }
    
    if (flag) puts("Yes"); 
    else puts("No");
    
    return 0;
}

二分图的最大匹配

给定一个二分图，其中左半部包含 n1 个点（编号 1∼n1），右半部包含 n2 个点（编号 1∼n2），二分图共包含 m 条边。

数据保证任意一条边的两个端点都不可能在同一部分中。请你求出二分图的最大匹配数。

#include <iostream>
#include <vector>
#include <cstring>

using namespace std;

const int N = 510, M = 100010, INF = 0x3f3f3f3f;

vector<int> g[N];
int match[N];
bool st[N];
int n1, n2, m;

bool find(int u) {
    for (int v : g[u]) {
        if (!st[v]) {
            st[v] = true;
            if (match[v] == 0 || find(match[v])) {
                match[v] = u;
                return true;
            }
        }
    }
    return false;
}

int main(void) {
    scanf("%d%d%d", &n1, &n2, &m);
    for (int i = 1; i <= m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        g[a].push_back(b);
    }
    
    int res = 0;
    for (int i = 1; i <= n1; ++i) {
        memset(st, 0, sizeof st);
        if (find(i)) res++;
    }
    
    cout << res;
    return 0;
}

最小路径重复点覆盖

#include <iostream>
#include <cstring>

using namespace std;

const int N = 210;

bool d[N][N], st[N];
int match[N];
int n, m;

bool find(int x) {
    for (int i = 1; i <= n; ++i) {
        if (!d[x][i] || st[i]) continue;

        st[i] = true;
        if (match[i] == 0 || find(match[i])) {
            match[i] = x;
            return true;
        }
    }
    return false;
}

int main(void) {
    cin >> n >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        d[a][b] = true;
    }

    // 传递闭包
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                d[i][j] |= d[i][k] && d[k][j];
            }
        }
    }

    int res = 0;
    for (int i = 1; i <= n; ++i) {
        memset(st, false, sizeof st);
        if (find(i)) res++;
    }

    cout << n - res;
    return 0;
}

欧拉回路

判断并打印回路（的边

/*
	边的编号从1开始，点的编号1~n
	type == 1 表示无向边，type == 2 表示有向边
	n，m为点数和边数
	存在欧拉回路打印YES，否则NO
	打印欧拉回路的一路径
*/

#include <iostream>
#include <cstring>

using namespace std;

const int N = 100010, M = 2 * 200010;

int h[N], ne[M], e[M], idx;
bool used[M];
int ru[N], chu[N];
int ans[M], cnt;
int type, n, m;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u) {

    for (int &i = h[u]; ~i;) {

        if (used[i]) {
            i = ne[i];
            continue;
        }

        used[i] = true;
        if (type == 1) used[i ^ 1] = true;

        int t;
        if (type == 1) {
            t = i / 2 + 1;
            if (i & 1) t = -t;
        } else t = i + 1;

        int v = e[i];
        i = ne[i];
        dfs(v);

        ans[++cnt] = t;
    }
}

int main(void) {
    
    scanf("%d%d%d", &type, &n, &m);
    
    memset(h, -1, sizeof h);

    for (int i = 1; i <= m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        ru[b]++, chu[a]++;
        if (type == 1) add(b, a);
    }

    if (type == 1) {
        for (int i = 1; i <= n; ++i) {
            if (ru[i] + chu[i] & 1) {
                puts("NO");
                return 0;
            }
        }
    } else {
        for (int i = 1; i <= n; ++i) {
            if (ru[i] != chu[i]) {
                puts("NO");
                return 0;
            }
        }
    }

    for (int i = 1; i <= n; ++i) {
        if (h[i] != -1) {
            dfs(i);
            break;
        }
    }

    if (cnt < m) {
        puts("NO");
        return 0;
    }
    
    puts("YES");
    for (int i = cnt; i; i--)
        printf("%d ", ans[i]);

    return 0;
}

字典序最小输出无向图的欧拉路径

/*
	按字典序遍历即可
	n个点（1~500），m个边，输出路径经过的顶点编号
*/

#include <iostream>

using namespace std;

const int N = 510, M = 1100;

int g[N][N];
int ans[M], cnt;
int du[N];
int n = 500, m;

void dfs(int u) {

    for (int i = 1; i <= n; ++i) {
        if (g[u][i]) {
            g[u][i]--, g[i][u]--;
            dfs(i);
        }
    }
    ans[++cnt] = u;
}

int main(void) {
    cin >> m;
    while (m--) {
        int a, b;
        cin >>a >> b;
        du[a]++, du[b]++;
        g[a][b]++, g[b][a]++;
    }

    int start = 1;
    while (!du[start]) start++;
    for (int i = 1; i <= n; ++i) {
        if (du[i] & 1) {
            start = i;
            break;
        }
    }

    dfs(start);

    for (int i = cnt; i; i--) cout << ans[i] <<endl;

    return 0;
}

LCA

给定一棵包含 n 个节点的有根无向树，节点编号互不相同，但不一定是 1∼n。

有 m 个询问，每个询问给出了一对节点的编号 x 和 y，询问 x 与 y 的祖孙关系。

输入格式
输入第一行包括一个整数 表示节点个数；

接下来 n 行每行一对整数 a 和 b，表示 a 和 b 之间有一条无向边。如果 b 是 −1，那么 a 就是树的根；

第 n+2 行是一个整数 m 表示询问个数；

接下来 m 行，每行两个不同的正整数 x 和 y，表示一个询问。

输出格式
对于每一个询问，若 x 是 y 的祖先则输出 1，若 y 是 x 的祖先则输出 2，否则输出 0。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 40010, M = N * 2;

int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][16];
int q[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void bfs(int root)
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;
    int hh = 0, tt = 0;
    q[0] = root;
    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                q[ ++ tt] = j;
                fa[j][0] = t;
                for (int k = 1; k <= 15; k ++ )
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];
            }
        }
    }
}

int lca(int a, int b)
{
    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 15; k >= 0; k -- )
        if (depth[fa[a][k]] >= depth[b])
            a = fa[a][k];
    if (a == b) return a;
    for (int k = 15; k >= 0; k -- )
        if (fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    return fa[a][0];
}

int main()
{
    scanf("%d", &n);
    int root = 0;
    memset(h, -1, sizeof h);

    for (int i = 0; i < n; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        if (b == -1) root = a;
        else add(a, b), add(b, a);
    }

    bfs(root);

    scanf("%d", &m);
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        int p = lca(a, b);
        if (p == a) puts("1");
        else if (p == b) puts("2");
        else puts("0");
    }

    return 0;
}