动态规划算法的一些模板

DP

最长上升子序列

#include <iostream>

using namespace std;

const int N = 100010;

int f[N], a[N];

int main(void) {
    int n;
    cin >> n;
    
    for (int i = 0; i < n; ++i) cin >> a[i];
    
    int len = 0;
    for (int i = 0; i < n; ++i) {
        int l = 0, r = len;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (f[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        f[r + 1] = a[i];
        len = max(r + 1, len);
    }
    
    cout << len << endl;;
    //for (int i = 1; i <= n; ++i) cout << f[i] << ' ';
    return 0;
}

最长公共子序列

小沐沐说，对于两个数列 A 和 B，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。
输出：
输出一个整数，表示最长公共上升子序列的长度。

#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
char a[N], b[N];
int f[N][N];

int main(void) {
    cin >> n >> m;
    cin >> a + 1 >> b + 1;
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
        }
    }
    
    cout << f[n][m];
    
    return 0;
}

最短编辑距离

给定两个字符串 A 和 B，现在要将 A 经过若干操作变为 B，可进行的操作有：

1. 删除–将字符串 A 中的某个字符删除。
2. 插入–在字符串 A 的某个位置插入某个字符。
3. 替换–将字符串 A 中的某个字符替换为另一个字符。

求最少操作次数

#include <iostream>

using namespace std;

const int N = 1010;

int f[N][N];
char a[N], b[N];

int main(void) {
    int n, m;
    cin >> n >> a + 1;
    cin >> m >> b + 1;
    
    for (int i = 0; i <= n; ++i) f[i][0] = i;
    for (int i = 0; i <= m; ++i) f[0][i] = i;
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
            if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
            else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
        }
    }
    
    cout << f[n][m];
    
    return 0;
}

整数划分

一个正整数 n 可以表示成若干个正整数之和，形如：n=n1+n2+…+nk，其中 n1≥n2≥…≥nk,k≥1。

我们将这样的一种表示称为正整数 n 的一种划分。

现在给定一个正整数 n，请你求出 n 共有多少种不同的划分方法。

背包写法：

#include <iostream>

using namespace std;

const int N = 1010, MOD = 1e9 + 7;

int f[N];

int main(void) {
    int n;
    cin >> n;
    
    f[0] = 1;
    for (int i = 1; i <= n; ++i)
        for (int j = i; j <= n; ++j)
            f[j] = (f[j] + f[j - i]) % MOD;
            
    cout << f[n];
    return 0;
}

其他算法

#include <iostream>

using namespace std;

const int N = 1010, MOD = 1e9 + 7;

int f[N][N];

int main(void) {
    // f[i][j]表示总和为i，总个数为j的方案数
    int n;
    cin >> n;
    
    f[1][1] = 1;
    f[0][0] = 1;
    
    for (int i = 2; i <= n; ++i)
        for (int j = 1; j <= i; ++j)
            f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % MOD;
    
    int res = 0;
    for (int i = 0; i <= n; ++i) res = (res + f[n][i]) % MOD;
    
    cout << res;
    return 0;
}

数字三角形模型

最低费用

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110;

int f[N][N], w[N][N];

int main(void) {
    int n;
    cin >> n;

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j)
            cin >> w[i][j];
    }
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (i == 1 && j == 1) f[i][j] = w[i][j];
            else {
                f[i][j] = 0x3f3f3f3f;
                if (i > 1) f[i][j] = f[i - 1][j] + w[i][j];
                if (j > 1) f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
            }
        }
    }
    
    cout << f[n][n];
    return 0;
    
}

走两次的最大值

#include <iostream>

using namespace std;

const int N = 110;

int f[N+N][N][N], w[N][N];

int main(void) {
    int n;
    cin >> n;
    int a, b, c;
    while (cin >> a >> b >> c, a || b || c) w[a][b] = c;
    
    for (int k = 2; k <= n + n; ++k) {
        for (int i1 = 1; i1 <= n; ++i1) {
            for (int i2 = 1; i2 <= n; ++i2) {
                int j1 = k - i1, j2 = k - i2;
                if (j1 < 1 || j1 > n || j2 < 1 || j2 > n) continue;
                
                int t = w[i1][j1];
                if (j1 != j2) t += w[i2][j2];
                int &v = f[k][i1][i2];
                
                v = max(v, f[k - 1][i1][i2] + t);
                v = max(v, f[k - 1][i1 - 1][i2 - 1] + t);
                v = max(v, f[k - 1][i1 - 1][i2] + t);
                v = max(v, f[k - 1][i1][i2 - 1] + t);
            }
        }
    }
    
    cout << f[n + n][n][n];
    return 0;
}

最长上升子序列模型

登山问题

先上去再下来，最多能浏览几个点呢？

#include <iostream>

using namespace std;

const int N = 1010;

int f[N], g[N], h[N];

int main(void) {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> h[i];
    
    for (int i = 1; i <= n; ++i) {
        f[i] = 1;
        for (int j = 1; j < i; ++j) {
            if (h[j] < h[i]) f[i] = max(f[i], f[j] + 1);
        }
    }
    
    for (int i = n; i; --i) {
        g[i] = 1;
        for (int j = n; j > i; --j) {
            if (h[j] < h[i]) g[i] = max(g[i], g[j] + 1);
        }
    }
    
    int res = 0;
    for (int i = 1; i <= n; ++i) res = max(res, f[i] + g[i] - 1);
    cout << res;
    return 0;
    
}

友好城市

一条河道分割南北两边的城市，给出n组相连的南北城市的坐标，最多有几组路线互不相交的城市？

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 5010;

struct Node {
    int a, b;
    bool operator< (const Node &t) const {
        return a < t.a;
    }
} c[N];

int f[N];

int main(void) {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> c[i].a >> c[i].b;
    
    sort(c + 1, c + n + 1);
    
    int res = 0;
    for (int i = 1; i <= n; ++i) {
        f[i] = 1;
        for (int j = 1; j < i; ++j) {
            if (c[j].b < c[i].b) f[i] = max(f[i], f[j] + 1);
        }
        res = max(res, f[i]);
    }
    
    cout << res;
    return 0;
    
}

最大上升子序列和

#include <iostream>

using namespace std;

const int N = 1010;

int f[N], w[N];

int main(void) {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> w[i];
    
    int res = 0;
    for (int i = 1; i <= n; ++i) {
        f[i] = w[i];
        for (int j = 1; j < i; ++j) {
            if (w[j] < w[i]) f[i] = max(f[i], f[j] + w[i]);
        }
        res = max(res, f[i]);
    }
    
    cout << res;
    return 0;
    
}

覆盖整个区间的最少有序序列问题

能覆盖整个序列最少的不上升子序列个数 == 该序列的最长上升子序列长度
能覆盖整个序列最少的不下降子序列个数 == 该序列最长下降子序列长度
/* 
求最长上升子序列最大长度
    int cnt = 0;
    for (int i = 0; i < n; ++i) {
        int k = 0;
        while (k < cnt && g[k] < w[i]) k++;
        g[k] = w[i];
        if (k >= cnt) cnt++;
    }
    cout << cnt;
*/

导弹防御系统

为了对抗附近恶意国家的威胁，R 国更新了他们的导弹防御系统。
一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。
例如，一套系统先后拦截了高度为 3 和高度为 4 的两发导弹，那么接下来该系统就只能拦截高度大于 4 的导弹。
给定即将袭来的一系列导弹的高度，请你求出至少需要多少套防御系统，就可以将它们全部击落。

#include <iostream>

using namespace std;

const int N = 55;

int w[N], up[N], down[N];
int ans, n;

void dfs(int u, int su, int sd) {
    if (su + sd >= ans) return ;
    if (u == n) {
        ans = su + sd;
        return ;
    }

    // up
    int k = 0;
    while (k < su && up[k] <= w[u]) k++;
    int t = up[k];
    up[k] = w[u];
    if (k >= su) dfs(u + 1, su + 1, sd);
    else dfs(u + 1, su, sd);
    up[k] = t;

    // down
    k = 0;
    while (k < sd && down[k] >= w[u]) k++;
    t = down[k];
    down[k] = w[u];
    if (k >= sd) dfs(u + 1, su, sd + 1);
    else dfs(u + 1, su, sd);
    down[k] = t;
}

int main(void) {
    while (cin >> n, n) {
        for (int i = 0; i < n; ++i) cin >> w[i];
        ans = n;
        dfs(0, 0, 0);
        cout << ans << endl;
    }

    return 0;
}

最长公共上升子序列

#include <iostream>

using namespace std;

const int N = 3010;

int f[N][N];
int a[N], b[N];

int main(void) {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    for (int i = 1; i <= n; ++i) cin >> b[i];

    for (int i = 1; i <= n; ++i) {
        int t = 1;
        for (int j = 1; j <= n; ++j) {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], t);
            if (b[j] < a[i]) t = max(t, f[i - 1][j] + 1);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; ++i) res = max(res, f[n][i]);
    cout << res;
    return 0;
}

打印路径

#include "bits/stdc++.h"

using namespace std;

const int N = 1010;

struct Node
{
    int a, b, id;

    bool operator< (const Node &t) const
    {
        if (a != t.a) return a < t.a;
        return b > t.b;
    }
} mouse[N];

int pre[N], f[N];

void dfs(int k)
{
    if (!k) return ;
    dfs(pre[k]);
    cout << mouse[k].id << endl;
}

int main(void)
{
    int n = 0;
    int a, b;
    while (cin >> a >> b)
    {
        ++n;
        mouse[n].a = a, mouse[n].b = b, mouse[n].id = n;
    }

    sort(mouse + 1, mouse + n + 1);

    int k = 1;
    for (int i = 1; i <= n; ++i)
    {
        f[i] = 1;
        for (int j = 1; j <= i; ++j)
        {
            if (mouse[i].a > mouse[j].a && mouse[i].b < mouse[j].b && f[i] < f[j] + 1)
            {
                f[i] = f[j] + 1;
                pre[i] = j;
            }
        }
        
        if (f[k] < f[i]) k = i;
    }

    cout << f[k] << endl;

    dfs(k);
    return 0;
}

背包模型

初始化总结

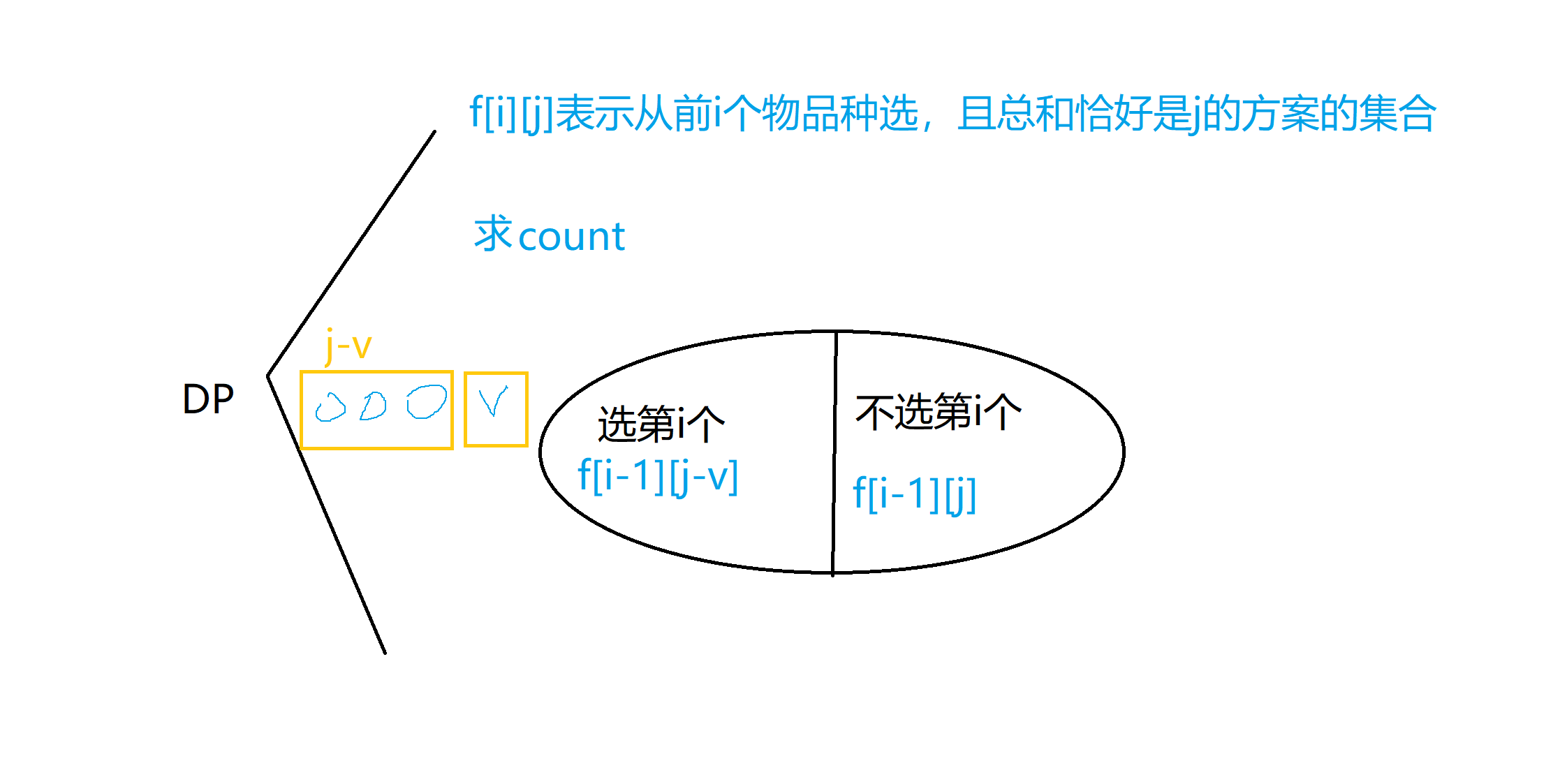
01背包求方案数

给定 N 个正整数 A1,A2,…,AN，从中选出若干个数，使它们的和为 M，求有多少种选择方案。

#include <iostream>

using namespace std;

const int N = 10010;

int f[N];

int main(void) {
    int n, m;
    cin >> n >> m;
    
    f[0] = 1;
    while (n--) {
        int v;
        cin >> v;
        for (int i = m; i >= v; --i)
            f[i] += f[i - v];
    }
    
    cout << f[m];
    return 0;
}

完全背包求方案数

给你一个n种面值的货币系统，求组成面值为m的货币有多少种方案。

n≤15,m≤3000

#include <iostream>

using namespace std;

const int N = 3010;

long long f[N];

int main(void) {
    int n, m;
    cin >> n >> m;
    
    f[0] = 1;
    while (n--) {
        int v;
        cin >> v;
        for (int i = v; i <= m; ++i) f[i] += f[i - v];
    }
    
    cout << f[m];
    return 0;
}

多重背包

#include <iostream>

using namespace std;

const int N = 6010;

int f[N];

int main(void) {
    int n, m;
    cin >> n >> m;
    while (n--) {
        int v, w, s;
        cin >> v >> w >> s;
        for (int i = m; i >= 0; --i) {
            for (int j = 0; j <= s && j * v <= i; ++j)
                f[i] = max(f[i], f[i - j * v] + j * w);
        }
    }
    
    cout << f[m];
    return 0;
}

多重背包II

0<N≤1000
0<V≤2000
0<vi,wi,si≤2000

#include <iostream>

using namespace std;

const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[M];

int main(void) {
    cin >> n >> m;

    int cnt = 0;
    for (int i = 1; i <= n; ++i) {
        int a, b, s;
        cin >> a >> b >> s;

        int k = 1;
        while (k <= s) {
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k <<= 1;
        }

        if (s > 0) {
            cnt++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }

    n = cnt;
    for (int i = 1; i <= n; ++i)
        for (int j = m; j >= v[i]; --j)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m];

    return 0;
}

多重背包III

0<N≤1000
0<V≤20000
0<vi,wi,si≤20000

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 20010;

int n, m;
int f[N], g[N], q[N];

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        int v, w, s;
        cin >> v >> w >> s;
        memcpy(g, f, sizeof f);
        for (int j = 0; j < v; j ++ )
        {
            int hh = 0, tt = -1;
            for (int k = j; k <= m; k += v)
            {
                if (hh <= tt && q[hh] < k - s * v) hh ++ ;
                while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt -- ;
                q[ ++ tt] = k;
                f[k] = g[q[hh]] + (k - q[hh]) / v * w;
            }
        }
    }

    cout << f[m] << endl;

    return 0;
}

混合背包问题

加二进制优化

#include <iostream>

using namespace std;

const int N = 1010;

int f[N];

int main(void) {
    int n, m;
    cin >> n >> m;
    
    while (n--) {
        int v, w, s;
        cin >> v >> w >> s;
        if (s == 0) {
            for (int i = v; i <= m; ++i) f[i] = max(f[i], f[i - v] + w);
        } else {
            if (s < 0) s = 1;
            for (int k = 1; k <= s; k <<= 1) {
                for (int i = m; i >= k * v; --i)
                    f[i] = max(f[i], f[i - k * v] + k * w);
                s -= k;
            }
            if (s) {
                for (int i = m; i >= s * v; --i)
                    f[i] = max(f[i], f[i - s * v] + s * w);
            }
        }
    }
    
    cout << f[m];
    return 0;
}

价值最小问题

状态定义：f[i][j]为体积至多为[i][j]的最小价值

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110;

int f[N][N];

int main(void) {
    int m1, m2, n;
    cin >> m1 >> m2 >> n;
    
    memset(f, 0x3f, sizeof f);
    f[0][0] = 0;
    
    while (n--) {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        for (int i = m1; i >= 0; --i) {
            for (int j = m2; j >= 0; --j) {
                f[i][j] = min(f[i][j], f[max(0, i - v1)][max(0, j - v2)] + w);
            }
        }
    }
    
    cout << f[m1][m2];
    return 0;
}

分组背包

#include <iostream>

using namespace std;

const int N = 110;

int f[N], v[N][N], w[N][N], s[N];

int main(void) {
    int n, m;
    cin >> n >> m;
    
    for (int i = 1; i <= n; ++i) {
        cin >> s[i];
        for (int j = 1; j <= s[i]; ++j)
            cin >> v[i][j] >> w[i][j];
    }
    
    for (int i = 1; i <= n; ++i) {
        for (int j = m; j >= 0; --j) {
            for (int k = 1; k <= s[i]; ++k)
                if (j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
        }
    }
    
    cout << f[m];
    return 0;
    
}

分组背包求方案数

总公司拥有M台 相同 的高效设备，准备分给下属的N个分公司。

各分公司若获得这些设备，可以为国家提供一定的盈利。盈利与分配的设备数量有关。

问：如何分配这M台设备才能使国家得到的盈利最大？

求出最大盈利值。

分配原则：每个公司有权获得任意数目的设备，但总台数不超过设备数M。

输入格式
第一行有两个数，第一个数是分公司数N，第二个数是设备台数M；

接下来是一个N*M的矩阵，矩阵中的第 i 行第 j 列的整数表示第 i 个公司分配 j 台机器时的盈利。

输出格式
第一行输出最大盈利值；

接下N行，每行有2个数，即分公司编号和该分公司获得设备台数。

答案不唯一，输出任意合法方案即可。

#include <iostream>

using namespace std;

const int N = 20, M = 20;

int f[N][M], w[N][N], way[N];

int main(void) {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1 ; j <= m; ++j)
            cin >> w[i][j];
    }
    
    for (int i = 1; i <= n; ++i) {
        for (int j = m; j >= 0; --j) {
            f[i][j] = f[i - 1][j];
            for (int k = 1; k <= j; ++k) 
                f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
        }
    }
    
    int j = m;
    for (int i = n; i; --i) {
        for (int k = 0; k <= m; ++k) {
            if (k <= j && f[i][j] == f[i - 1][j - k] + w[i][k]) {
                way[i] = k;
                j -= k;
                break;
            }
        }
    }
    
    cout << f[n][m] << endl;
    for (int i = 1; i <= n; ++i) cout << i << ' ' << way[i] << ' ' << endl;
    
}

有依赖的背包问题

(分组背包)
有 N 个物品和一个容量是 V 的背包。
物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。
每件物品的编号是 i，体积是 vi，价值是 wi，依赖的父节点编号是 pi。物品的下标范围是 1…N。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。

#include <iostream>
#include <vector>

using namespace std;

const int N = 110;

int f[N][N], v[N], w[N];
vector<int> g[N];
int n, m;

void dfs(int u) {

    for (int ne : g[u]) { // 枚举物品
        dfs(ne);

        for (int i = m - v[u]; i >= 0; --i) { //  枚举体积，给w[u]留空间
            for (int j = 0; j <= i; ++j) { // 枚举方案，方案为体积
                f[u][i] = max(f[u][i], f[u][i - j] + f[ne][j]);
            }
        }
    }

    for (int i = m; i >= v[u]; --i) f[u][i] = f[u][i - v[u]] + w[u]; // 添加w[u]
    for (int i = 0; i < v[u]; ++i) f[u][i] = 0; // 不符合情况为0
}

int main(void) {
    cin >> n >> m;
    int root = -1;
    for (int i = 1; i <= n; ++i) {
        int a, b, p;
        cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;
        else g[p].push_back(i);
    }

    dfs(root);
    cout << f[root][m];
    return 0;
}

求最优方案数

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 最优选法的方案数。注意答案可能很大，请输出答案模 109+7 的结果。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, MOD = 1e9 + 7;

int f[N], g[N];

int main(void) {
    int n, m;
    cin >> n >> m;
    
    memset(f, -0x3f, sizeof f);
    f[0] = 0; // 体积恰好为j的最大价值
    g[0] = 1;
    
    while (n--) {
        int v, w;
        cin >> v >> w;
        for (int i = m; i >= v; --i) {
            int val = max(f[i], f[i - v] + w);
            int cnt = 0;
            if (val == f[i]) cnt = g[i];
            if (val == f[i - v] + w) cnt = (cnt + g[i - v]) % MOD;
            g[i] = cnt;
            f[i] = val;
        }
    }
    
    int res = 0;
    for (int i = 0; i <= m; ++i) res = max(res, f[i]);
    
    int cnt = 0;
    for (int i = 0; i <= m; ++i) {
        if (res == f[i]) cnt = (cnt + g[i]) % MOD;
    }
    
    cout << cnt;
    
    return 0;
}

求具体方案

字典序最小

#include <iostream>

using namespace std;

const int N = 1010;

int f[N][N], v[N], w[N];

int main(void) {
    int n, m;
    cin >> n >> m;
    
    for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
    
    for (int i = n; i >= 1; --i) {
        for (int j = 0; j <= m; ++j) {
            f[i][j] = f[i + 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    }
    
    int j = m;
    for (int i = 1; i <= n; ++i) {
        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) {
            cout << i << ' ';
            j -= v[i];
        }
    }
    
    return 0;
}

状态机模型

不能选择两个连续的

你是一名盗贼，现在有n家店铺，你不能连续的偷两个店铺，问最多能偷盗多少钱

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int w[N], f[N][2];

void solve() {
    //f[0][0] = 0, f[0][1] = -0x3f3f3f3f;

    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> w[i];

    for (int i = 1; i <= n; ++i) {
        f[i][0] = max(f[i - 1][0], f[i - 1][1]);
        f[i][1] = f[i - 1][0] + w[i];
    }

    cout << max(f[n][0], f[n][1]) << endl;
}

int main(void) {
    int T;
    cin >> T;
    while (T--)
        solve();

    return 0;
}

股票买卖IV

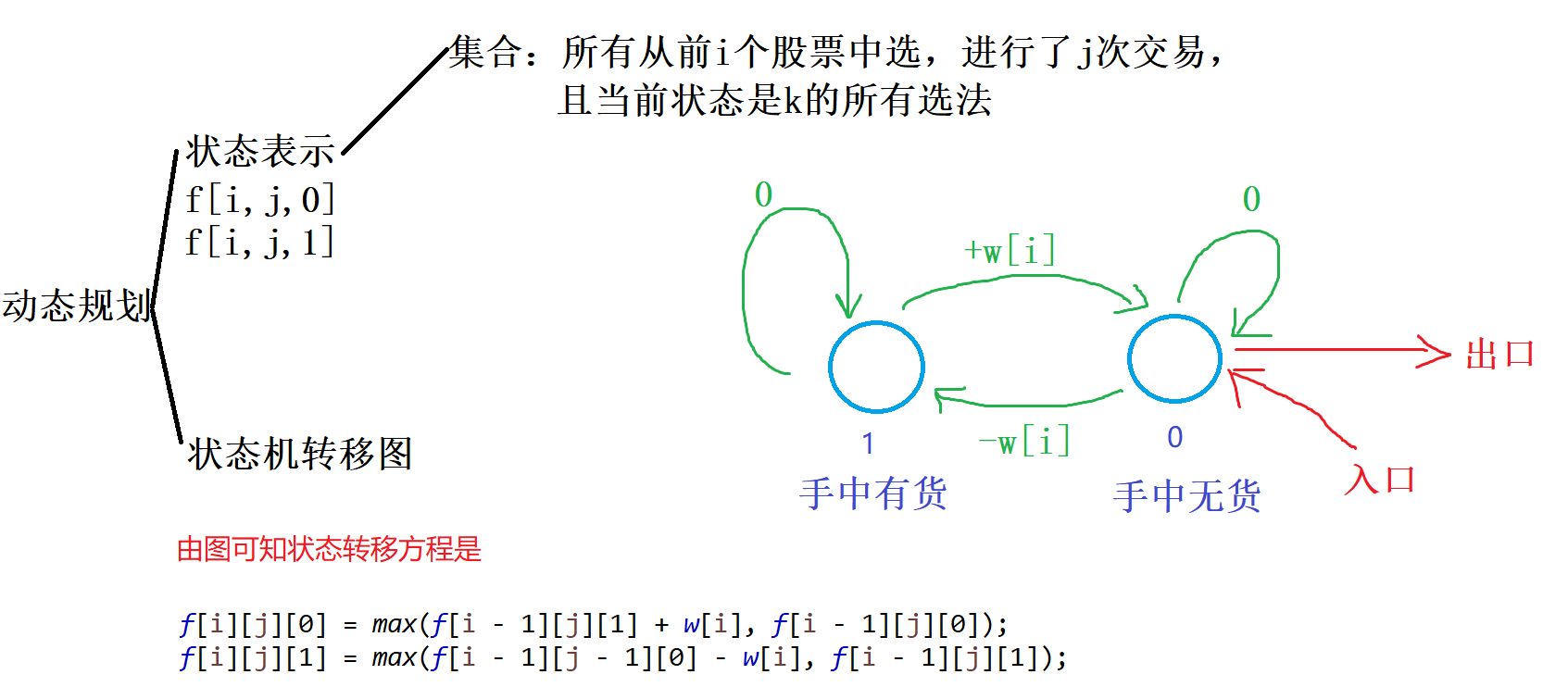
给定一个长度为 N 的数组，数组中的第 i 个数字表示一个给定股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 100010, K = 110;

int f[N][K][2], w[N]; // 在前i个股票中，第j个交易时，手中无货0，有货1

int main(void) {
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    
    memset(f, -0x3f, sizeof f);
    for (int i = 0; i <= n; ++i) f[i][0][0] = 0;
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= k; ++j) {
            f[i][j][1] = max(f[i - 1][j - 1][0] - w[i], f[i - 1][j][1]);
            f[i][j][0] = max(f[i - 1][j][1] + w[i], f[i - 1][j][0]);
        }
    }
    
    int res = 0;
    for (int i = 0; i <= k; ++i) res = max(res, f[n][i][0]);
    cout << res;
    return 0;
}

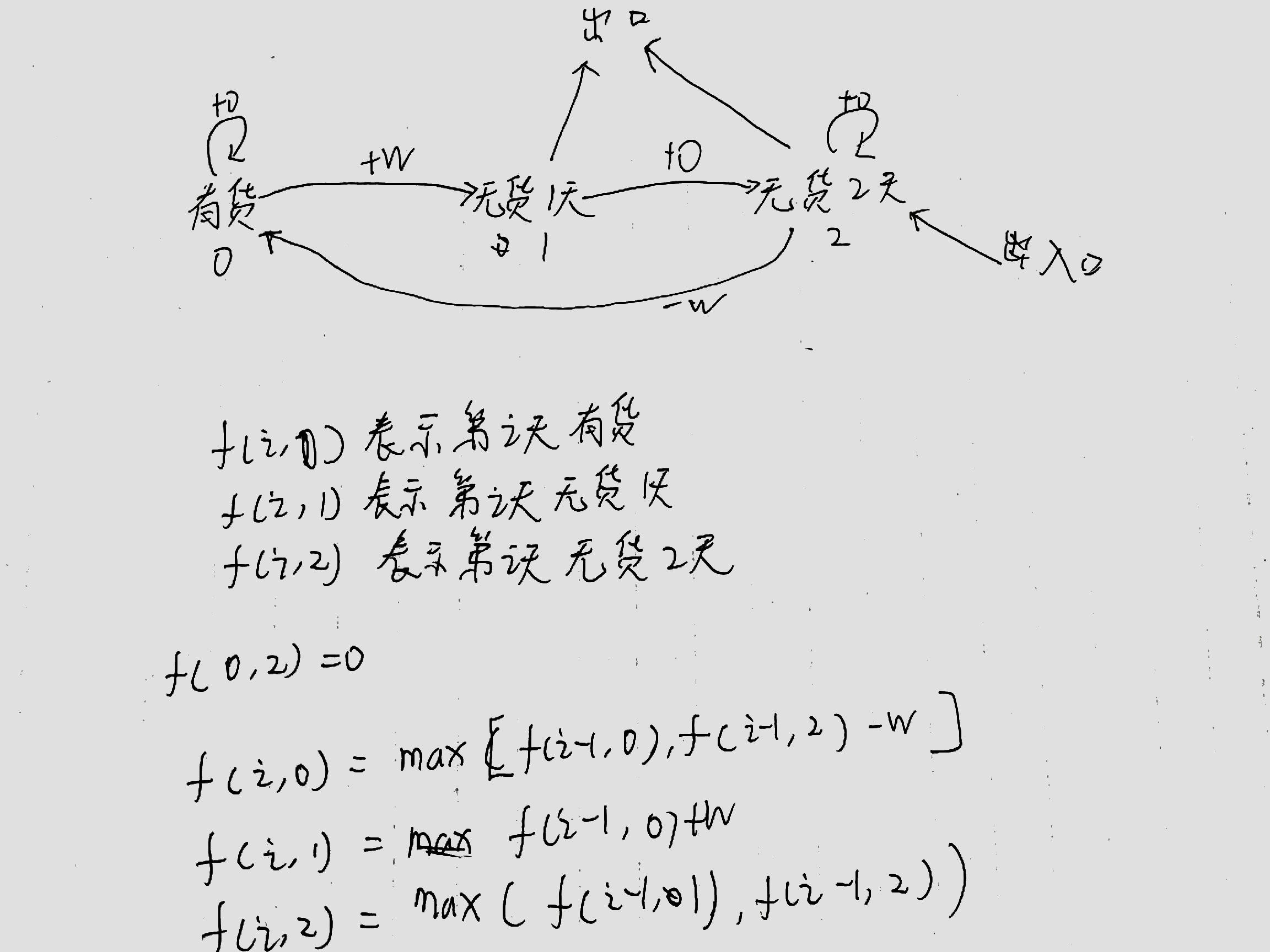
股票买卖V

给定一个长度为 N 的数组，数组中的第 i 个数字表示一个给定股票在第 i 天的价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
    你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
    卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 100010;

int f[N][3], w[N];

int main(void) {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    
    memset(f, -0x3f, sizeof f);
    f[0][1] = f[0][2] = 0;
    
    for (int i = 1; i <= n; ++i) {
        f[i][0] = max(f[i - 1][0], f[i - 1][2] - w[i]);
        f[i][1] = max(f[i - 1][1], f[i - 1][0] + w[i]);
        f[i][2] = max(f[i - 1][1], f[i - 1][2]);
    }
    
    cout << max(f[n][1], f[n][2]);
    return 0;
}

状态压缩模型

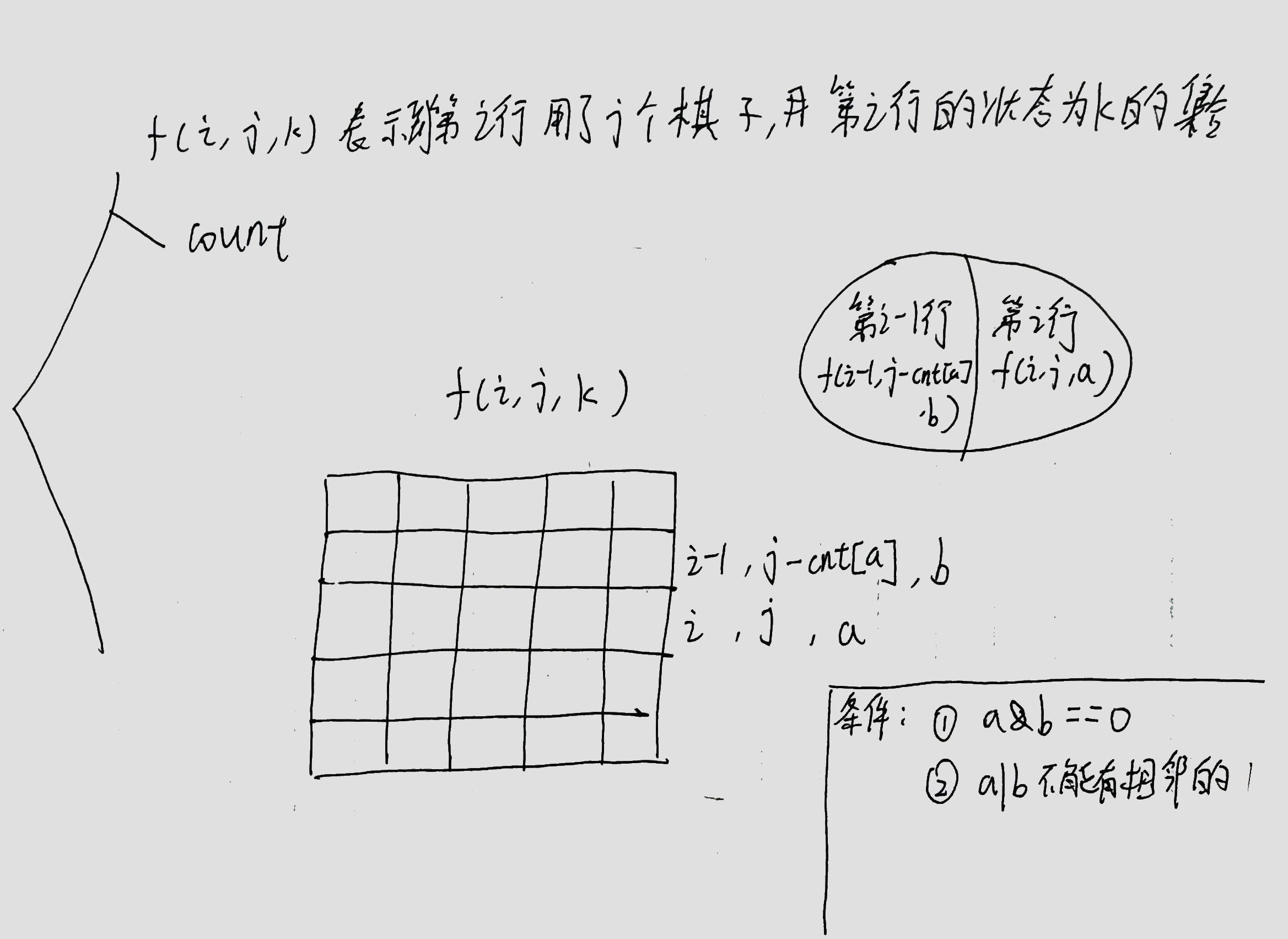
小国王

在 n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。

#include <iostream>
#include <vector>

using namespace std;

const int N = 15, M = 1 << 10, K = 120;

long long f[N][K][M];
vector<int> state;
vector<int> head[M]; // 可由状态i转移到状态j
int cnt[M]; // 存储状态i有多少个1
int n, k;

bool check(int x) {
    for (int i = 0; i < n; ++i) {
        if (x >> i & 1 && x >> i + 1 & 1) return false;
    }
    return true;
}

int count(int x) {
    int res = 0;
    for (int i = 0; i < n; ++i) res += x >> i & 1;
    return res;
}

int main(void) {
    cin >> n >> k;

    for (int i = 0; i < 1 << n; ++i) {
        if (check(i)) {
            state.push_back(i);
            cnt[i] = count(i);
        }
    }

    for (int i = 0; i < state.size(); ++i) {
        for (int j = 0; j < state.size(); ++j) {
            int  a = state[i], b = state[j];
            if ((a & b) == 0 && check(a | b)) head[i].push_back(j); // 无向的
        }
    }

    f[0][0][0] = 1;
    for (int i = 1; i <= n + 1; ++i) {
        for (int j = 0; j <= k; ++j) {
            for (int a = 0; a < state.size(); ++a) {
                for (int b : head[a]) {
                    int c = cnt[state[a]];
                    if (j >= c) f[i][j][a] += f[i-1][j-c][b];
                }
            }
        }
    }

    cout << f[n + 1][k][0];
    return 0;
}

玉米田

农夫约翰的土地由 M×N 个小方格组成，现在他要在土地里种植玉米。

非常遗憾，部分土地是不育的，无法种植。

而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。

现在给定土地的大小，请你求出共有多少种种植方法。

土地上什么都不种也算一种方法。

#include <iostream>
#include <vector>

using namespace std;

const int N = 13, M = 1 << N, MOD = 1e8;

int f[N][M]; // 第i行的状态为j
int w[M]; // 第i行的状态，1表示不育，
vector<int> state;
vector<int> g[M];

int n, m;

bool check(int x) {
    for (int i = 0; i < m; ++i)
        if (x >> i & 1 && x >> i + 1 & 1) return false;
    return true;
}

int main(void) {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        for (int j = 0; j < m; ++j) {
            int x;
            cin >> x;
            w[i] = w[i] * 2 + !x;
        }
    }

    for (int i = 0; i < 1 << m; ++i) {
        if (check(i)) state.push_back(i);
    }

    for (int i = 0; i < state.size(); ++i) {
        for (int j = 0; j < state.size(); ++j) {
            int a = state[i], b = state[j];
            if ((a & b) == 0) g[j].push_back(i);
        }
    }

    f[0][0] = 1;
    for (int i = 1; i <= n + 1; ++i) {
        for (int a = 0; a < state.size(); ++a) {
            for (int b : g[a]) {
                if ((state[a] & w[i]) == 0 && (state[b] & w[i - 1]) == 0) {
                    f[i][a] = (f[i][a] + f[i - 1][b]) % MOD;
                }
            }
        }
    }

    cout << f[n + 1][0];
    return 0;
}

炮兵阵地

  *
  *
**X**
  *
  *
  
  若在x处放置炮车，*区域均不能放置
  给定一张n*m的图，图中H点固定不能放大炮
  在n*m的网络中，最多可以放多少个大炮？

#include <iostream>
#include <vector>

using namespace std;

const int N = 110, M = 1 << 11;

long long f[2][M][M]; // 第i行，第i行的状态，第i-1行的状态
int w[N]; // 第i行的状态，1表示不能放大炮
vector<int> state;
vector<int> g[M];
int cnt[M];

int n, m;

bool check(int x) {
    for (int i = 0; i < m; ++i) {
        if (x >> i & 1 && (x >> i + 1 & 1 || x >> i + 2 & 1)) return false;
    }
    return true;
}

int count(int x) {
    int res = 0;
    for (int i = 0; i < m; ++i) res += x >> i & 1;
    return res;
}

int main(void) {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        string s;
        cin >> s;
        for (int j = 0; j < m; ++j) {
            char ch = s[j];
            int t = ch == 'H';
            w[i] = w[i] * 2 + t;
        }
    }

    for (int i = 0; i < 1 << m; ++i) {
        if (check(i)) {
            state.push_back(i);
            cnt[i] = count(i);
        }
    }

    for (int i = 1; i <= n; ++i) {
        for (int u = 0; u < state.size(); ++u) { // i
            for (int v = 0; v < state.size(); ++v) { // i - 1
                for (int k = 0; k < state.size(); ++k) { // i - 2
                    int a = state[u], b = state[v], c = state[k];
                    if (a & b | a & c | b & c) continue;
                    if (w[i] & a | w[i - 1] & b) continue;
                    //if (i >= 2 && w[i - 2] & c) continue;
                    f[i & 1][u][v] = max(f[i & 1][u][v], f[i - 1 & 1][v][k] + cnt[a]);
                }
            }
        }
    }

    long long res = 0;
    for (int i = 0; i < state.size(); ++i) {
        for (int j = 0; j < state.size(); ++j)
            res = max(res, f[n & 1][i][j]);
    }

    cout << res;
    return 0;
}

区间问题

环形石子合并

将 n 堆石子绕圆形操场排放，现要将石子有序地合并成一堆。

规定每次只能选相邻的两堆合并成新的一堆，并将新的一堆的石子数记做该次合并的得分。

请编写一个程序，读入堆数 n 及每堆的石子数，并进行如下计算：

选择一种合并石子的方案，使得做 n−1 次合并得分总和最大。
选择一种合并石子的方案，使得做 n−1 次合并得分总和最小。

#include <iostream>

using namespace std;

const int N = 210;

int f[N][N], g[N][N];
int w[N], s[N];
int n;

int main(void) {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> w[i];
    for (int i = n + 1; i <= n + n; ++i) w[i] = w[i - n];
    
    for (int i = 1; i <= n + n; ++i) s[i] = s[i - 1] + w[i];
    
    for (int len = 1; len <= n; ++len) {
        for (int l = 1; l + len - 1 <= n + n; ++l) {
            int r = l + len - 1;
            if (l == r) continue;
            f[l][r] = 2e9, g[l][r] = -2e9;
            for (int k = l; k < r; ++k) {
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
                g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
            }
        }
    }
    
    int minv = 2e9, maxv = -2e9;
    for (int i = 1; i <= n; ++i) {
        minv = min(minv, f[i][i + n - 1]);
        maxv = max(maxv, g[i][i + n - 1]);
    }
    
    cout << minv << endl << maxv;
    return 0;
}

加分二叉树

设一个 n 个节点的二叉树 tree 的中序遍历为（1,2,3,…,n），其中数字 1,2,3,…,n 为节点编号。

每个节点都有一个分数（均为正整数），记第 i 个节点的分数为 di，tree 及它的每个子树都有一个加分，任一棵子树 subtree（也包含 tree 本身）的加分计算方法如下：     

subtree的左子树的加分 × subtree的右子树的加分 ＋ subtree的根的分数 

若某个子树为空，规定其加分为 1。

叶子的加分就是叶节点本身的分数，不考虑它的空子树。

试求一棵符合中序遍历为（1,2,3,…,n）且加分最高的二叉树 tree。

要求输出： 

（1）tree的最高加分 

（2）tree的前序遍历

#include <iostream>

using namespace std;

const int N = 35;

int w[N], f[N][N], g[N][N];
int n;

void dfs(int l, int r) {
    if (l > r) return ;
    
    cout << g[l][r] << ' ';
    int k = g[l][r];
    dfs(l, k - 1);
    dfs(k + 1, r);
    
}

int main(void) {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> w[i];
    
    for (int len = 1; len <= n; ++len) {
        for (int i = 1; i + len - 1 <= n; ++i) {
            int j = i + len - 1;
            if (i == j) f[i][j] = w[i], g[i][j] = i;
            else {
                f[i][j] = -2e9;
                for (int k = i; k <= j; ++k) {
                    int left = i == k ? 1 : f[i][k - 1];
                    int right = j == k ? 1 : f[k + 1][j];
                    int t = left * right + w[k];
                    if (f[i][j] < t) {
                        f[i][j] = t;
                        g[i][j] = k;
                    }
                }
            }
        }
    }
    
    cout << f[1][n] << endl;
    dfs(1, n);
    return 0;
}

树上DP

树的最长路径

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

现在请你找到树中的一条最长路径。

换句话说，要找到一条路径，使得使得路径两端的点的距离最远。

注意：路径中可以只包含一个点。

1≤n≤10000,
1≤ai,bi≤n,
−105≤ci≤105

#include <iostream>
#include <vector>

using namespace std;

const int N = 10010;

vector<pair<int, int>> g[N];
int n, ans;

int dfs(int u, int fa) {
    
    int d1 = 0, d2 = 0, dist = 0;
    for (auto t : g[u]) {
        int v = t.first, val = t.second;
        if (v == fa) continue;
        int d = dfs(v, u) + val;
        if (d > d1) d2 = d1, d1 = d;
        else if (d > d2) d2 = d;
        dist = max(dist, d);
    }
    
    ans = max(ans, d1 + d2);
    return dist;
}

int main(void) {
    cin >> n;
    for (int i = 1; i < n; ++i) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a].push_back({b, c});
        g[b].push_back({a, c});
    }
    
    dfs(1, -1);
    cout << ans;
    return 0;
    
}

树的中心

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。

1≤n≤10000,
1≤ai,bi≤n,
1≤ci≤105

#include <iostream>
#include <vector>

using namespace std;

typedef pair<int, int> PII;

const int N = 10010, INF = 0x3f3f3f3f;

vector<PII> g[N];
int d1[N], d2[N], up[N], p1[N], p2[N];
int n;

int dfs_down(int u, int fa) {
    
    d1[u] = d2[u] = -INF;
    for (PII t : g[u]) {
        int v = t.first, val = t.second;
        if (v == fa) continue;
        
        int d = dfs_down(v, u) + val;
        if (d > d1[u]) {
            d2[u] = d1[u], d1[u] = d;
            p2[u] = p1[u], p1[u] = v;
        } else if (d > d2[u]) {
            d2[u] = d;
            p2[u] = v;
        }
    }
    
    if (d1[u] == -INF) d1[u] = d2[u] = 0;
    return d1[u];
}

void dfs_up(int u, int fa) {
    
    for (PII t : g[u]) {
        int v = t.first, val = t.second;
        if (v == fa) continue;
        if (p1[u] == v) up[v] = max(up[u], d2[u]) + val;
        else up[v] = max(up[u], d1[u]) + val;
        
        dfs_up(v, u);
    }
}

int main(void) {
    cin >> n;
    for (int i = 1; i < n; ++i) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a].push_back({b, c});
        g[b].push_back({a, c});
    }
    
    dfs_down(1, -1);
    dfs_up(1, -1);
    
    int res = INF;
    for (int i = 1; i <= n; ++i) res = min(res, max(up[i], d1[i]));
    cout << res;
    return 0;
}

数字转换

如果一个数 x 的约数之和 y（不包括他本身）比他本身小，那么 x 可以变成 y，y 也可以变成 x。

例如，4 可以变为 3，1 可以变为 7。

限定所有数字变换在不超过 n 的正整数范围内进行，求不断进行数字变换且不出现重复数字的最多变换步数。
1≤n≤50000

#include <iostream>
#include <vector>

using namespace std;

const int N = 50010;

vector<int> g[N];
int sum[N];
int n, ans;

int dfs(int u, int fa) {
    
    int d1 = 0, d2 = 0;
    for (int v : g[u]) {
        if (v == fa) continue;
        int d = dfs(v, u) + 1;
        if (d > d1) d2 = d1, d1 = d;
        else if (d > d2) d2 = d;
    }
    
    ans = max(ans, d1 + d2);
    return d1;
}

int main(void) {
    scanf("%d", &n);
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 2; j <= n / i; ++j) {
            sum[i * j] += i; // sum存储x的约数和(不包括x本身)
        }
    }
    
    for (int i = 1; i <= n; ++i) {
        if (sum[i] < i) {
            g[sum[i]].push_back(i);
            g[i].push_back(sum[i]);
        }
    }
    
    dfs(1, -1);
    cout << ans;
    return 0;
}

二叉苹果树

有一棵二叉苹果树，如果树枝有分叉，一定是分两叉，即没有只有一个儿子的节点。

这棵树共 N 个节点，编号为 1 至 N，树根编号一定为 1。

我们用一根树枝两端连接的节点编号描述一根树枝的位置。

一棵苹果树的树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。

这里的保留是指最终与1号点连通。

#include <iostream>
#include <vector>

using namespace std;

typedef pair<int, int>  PII;

const int N = 110;

int f[N][N]; // 以i为子树，选j条边的最大价值
vector<PII> g[N];
int n, m;

void dfs(int u, int fa) {
    
    for (PII t : g[u]) {
        int v = t.first, val = t.second;
        if (v == fa) continue;
        dfs(v, u);
        
        for (int i = m; i >= 0; --i) {
            for (int k = 0; k < i; ++k) {
                f[u][i] = max(f[u][i], f[u][i - k - 1] + f[v][k] + val);
            }
        }
    }
}

int main(void) {
    cin >> n >> m;
    for (int i = 1; i < n; ++i) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a].push_back({b, c});
        g[b].push_back({a, c});
    }
    
    dfs(1, -1);
    cout << f[1][m];
    return 0;
}