[POJ1003]Hangover
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 111811 | Accepted: 54608 |
Description
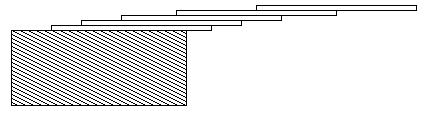
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.
Input
Output
Sample Input
1.00 3.71 0.04 5.19 0.00
Sample Output
3 card(s) 61 card(s) 1 card(s) 273 card(s)
Source
思路
级数求和

var n,k:real; procedure main; var i:longint; begin i:=1;k:=0; while k<n do begin inc(i); k:=k+(1/i); end; writeln(i-1,' card(s)'); end; begin while true do begin read(n); if n=0 then halt; main; end; end.




