二项分布及其极大似然估计
一、二项分布
二项分布：即n次独立重复试验，在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当n = 1时，二项分布就是伯努利分布。
伯努利分布的数学公式表达如下：
如果表示抛硬币,则正面向上的概率为x=1时，p(1)=p^1*(1-p)^(1-1)=p,反面向上的概率为x=0时，p(0)=p^0*(1-p)=1-p
由此可得：多次抛硬币就是一个二项分布，其数学公式可表示为：
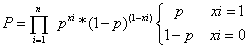
注：这里xi的下标i截图看的不清，就这样表示。
二、极大似然估计
极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！
由上面可知，二项分布的损失函数表示为：
根据梯度下降的方法对二项分布的极大似然估计进行证明，对p进行求导：
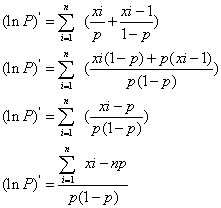
所以极值点为，也是其极大似然估计：
其中：n为总共实验的次数，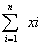
为正样本出现的次数
比如抛硬币实验： 100次，正面次数80，反面次数20，这样其极大似然估计为0.8
参考博客：1、一文搞懂极大似然估计
