基于模型(矩阵分解)的推荐(u2i)
一、算法分类
基于模型的协同过滤作为目前最主流的协同过滤类型,当只有部分用户和部分物品之间是有评分数据的,其他部分评分是空白,此时我们要用已有的部分稀疏数据来预测那些空白的用户和物品之间的评分关系,找到最高评分的物品推荐给用户,实现用户对未评价过的物品的预测评分。
基于模型协同过滤的方法包括:用关联算法、聚类算法、分类算法、回归算法、矩阵分解、神经网络,图模型以及隐语义模型来解决。
本文讲矩阵分解的推荐。
二、基本思想
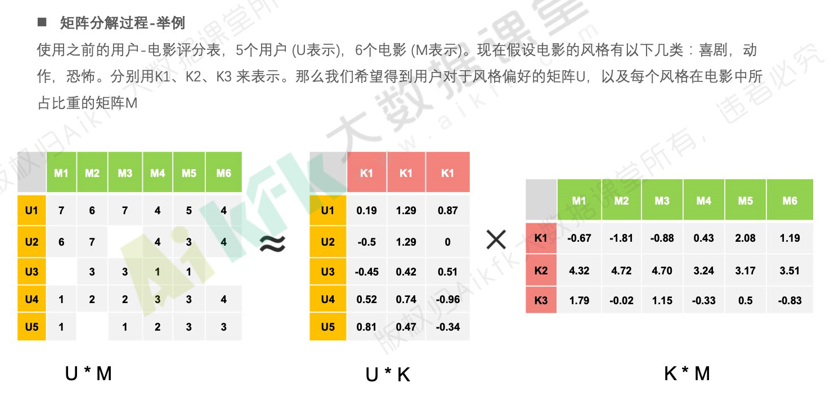
矩阵分解,直观上来说就是把原来的大矩阵,近似分解成两个小矩阵的乘积,在实际推荐计算时不再使用大矩阵,而是使用分解得到的两个小矩阵。按照矩阵分解的原理,把原来的m*n 的大矩阵会分解成 m*k和k*n的两个小矩阵。
k:隐式向量的维度数,是一个超参需要提前制定,k的取值远远小于m和n。
三、优缺点
| 优点 | 缺点 |
|
比较容易编程实现,随机梯度下降方法依次迭代即可训练出模型。 比较低的时间和空间复杂度,高维矩阵映射为两个低维矩阵节省了存储空间, 训练过程比较费时,但是可以离线完成; 评分预测一般在线计算,直接使用离线训练得到的参数,可以实时推荐。 |
模型训练比较费时。 |
| 预测的精度比较高,预测准确率要高于基于领域的协同过滤以及内容过滤等方法。 |
推荐结果不具有很好的解释性,分解出来的用户和物品 矩阵的每个维度无法和现实生活中概念来解释, 无法用现实概念给每个维度命名,只能理解为在语义空间。 |
四、实现算法
1、交替最小二乘法(ALS)
ALS优势:
(1) 在交替的其中一步,也就是假设已知其中一个矩阵求解另一个矩阵时,要优化的参数是很容易并行化的;
(2) 在不那么稀疏的数据集合上,交替最小二乘通常比随机梯度下降要更快的得到结果。
ALS过程:
(1) 初始化随机矩阵U里面的元素值;
(2) 把U矩阵当做已知的,直接用线性代数的方法求得矩阵V;
(3) 得到的矩阵V后,把V当做已知的,求解矩阵U;
(4) 上面两个过程交替进行,一直到误差可以接受为止。
测试数据

1,1,7.0 1,2,6.0 1,3,7.0 1,4,4.0 1,5,5.0 1,6,4.0 2,1,6.0 2,2,7.0 2,4,4.0 2,5,3.0 2,6,4.0 3,2,3.0 3,3,3.0 3,4,1.0 3,5,1.0 4,1,1.0 4,2,2.0 4,3,2.0 4,4,3.0 4,5,3.0 4,6,4.0 5,1,1.0 5,3,1.0 5,4,2.0 5,5,3.0 5,6,3.0
spark代码:

import org.apache.spark.ml.evaluation.RegressionEvaluator import org.apache.spark.ml.recommendation.ALS import org.apache.spark.ml.recommendation.ALS.Rating import org.apache.spark.sql.SparkSession object ALSRecommend_test { def main(args: Array[String]): Unit = { val spark = SparkSession.builder() .master("local[5]") .getOrCreate() import spark.implicits._ //1.准备源数据集 val movieRatings = spark.read.textFile("E:\\tmp\\aikfka\\movieLess\\utou_main.csv") .map(line => { val fields = line.split(",") Rating(fields(0).toInt , fields(1).toInt , fields(2).toFloat) }) //2.从源数据集中拆分出一部分作为训练集 val Array(traing,test) = movieRatings.randomSplit(Array(0.8 , 0.2)) //3.用训练集来训练一个模型 val als = new ALS() .setMaxIter(15) .setUserCol("user") .setItemCol("item") .setRatingCol("rating") .setRegParam(0.15) //避免过拟合 .setRank(5) val model = als.fit(traing) model.itemFactors.show(false) model.userFactors.show(false) // // //在打分数据里面,有这样的情况,就是数据集切割之后,用户对电影的评分有不完整的情况,就是测试集里面可能会出现训练集当中 // //没有出现过的电影或者用户 // //这个叫做冷启动 // //ALS有两种策略,一种是标识为NAN,还有一种是丢弃掉。我们这里选择丢掉 // model.setColdStartStrategy("drop") // // //4.通过模型来预测我们的测试集(源数据中的另一部分) // val prediction = model.transform(test) // // //5.通过指标来评估模型的好坏(也就是预测的评分结果和测试集中的用户的评分结果的误差值大小) // //我们使用RMSE指标来判断模型的好坏,其实就是真实评分和预测评分的评分和 // //RMSE的结果越小,实际的模型的效果就越好 // //这里要数据真实值的一列和预测值的一列 // val evaluator = new RegressionEvaluator() // .setMetricName("rmse") // .setLabelCol("rating") // .setPredictionCol("prediction") // // val rmse = evaluator.evaluate(prediction) // // println("评估值:" + rmse) // // //6.基于模型完成物品的推荐 // //// Returns top `numItems` items recommended for each user, for all users. // //为每一个用户推荐10个商品 // val forUserRecommendItem = model.recommendForAllUsers(6) // forUserRecommendItem.show(false) // // // //Returns top `numUsers` users recommended for each item, for all items. // //为每一个商品推荐10个用户 // val forItemRecommendUser = model.recommendForAllItems(10) // // // //为指定的用户推荐商品 // val users = movieRatings.select(als.getUserCol).distinct().limit(5) // // val userSubset = model.recommendForUserSubset(users , 10) // //// val items = movieRatings.select(als.getItemCol).distinct().limit(5) //// //// val itemSubset = model.recommendForItemSubset(items , 10) // // userSubset.show(false) //// itemSubset.show(false) } }
2、随机梯度下降
(1) 确定优化目标
优化目标是让,Mij和Sij越接近越好,误差越小越好。(Mij是用户物品真实评分矩阵,Sij是预测评分矩阵)
loss = sum(i-->m,j--->n(Mij-Sij)^2)
(2) 确定loss里面的未知数是什么,从而优化他
loss=(Mij-Ui*Vj)^2
梯度下降,来找到最优的U、V;核心是找到函数的最小值点(迭代的方式)
(3) 梯度下降的过程
step1:loss对要下降的参数求导
dloss/dUi=2(Mij-Ui*Vj)*Vj
dloss/dVj=2(Mij-Ui*Vj)*Ui
step2:初始化一个Ui,Vj
for t in range(iter_numm):
Vt+1=Vt-lr(学习率)*dloss/dVj|Vj=Vt
python代码:

''' BiasSvd Model ''' import math import random import pandas as pd import numpy as np class BiasSvd(object): def __init__(self, alpha, reg_p, reg_q, reg_bu, reg_bi, number_LatentFactors=100, number_epochs=10, columns=["userId", "movieId", "rating"]): self.alpha = alpha # 学习率 self.reg_p = reg_p self.reg_q = reg_q self.reg_bu = reg_bu self.reg_bi = reg_bi self.number_LatentFactors = number_LatentFactors # 隐式类别数量 k 隐矩阵的维度 self.number_epochs = number_epochs # 迭代次数 梯度下降 self.columns = columns def fit(self, dataset): ''' fit dataset :param dataset: uid, iid, rating :return: ''' self.dataset = pd.DataFrame(dataset) self.users_ratings = dataset.groupby(self.columns[0]).agg([list])[[self.columns[1], self.columns[2]]] self.items_ratings = dataset.groupby(self.columns[1]).agg([list])[[self.columns[0], self.columns[2]]] self.globalMean = self.dataset[self.columns[2]].mean() self.P, self.Q, self.bu, self.bi = self.sgd() def _init_matrix(self): ''' 初始化P和Q矩阵,同时为设置0,1之间的随机值作为初始值 :return: ''' # User-LF P = dict(zip( self.users_ratings.index, np.random.rand(len(self.users_ratings), self.number_LatentFactors).astype(np.float32) )) # Item-LF Q = dict(zip( self.items_ratings.index, np.random.rand(len(self.items_ratings), self.number_LatentFactors).astype(np.float32) )) return P, Q def sgd(self): ''' 使用随机梯度下降,优化结果 :return: ''' #P ,Q 代表 P用户矩阵 Q 物品矩阵 参数矩阵 P, Q = self._init_matrix() # 初始化bu、bi的值,全部设为0 bu = dict(zip(self.users_ratings.index, np.zeros(len(self.users_ratings)))) bi = dict(zip(self.items_ratings.index, np.zeros(len(self.items_ratings)))) for i in range(self.number_epochs): print("iter%d"%i) error_list = [] for uid, iid, r_ui in self.dataset.itertuples(index=False): v_pu = P[uid] v_qi = Q[iid] # 梯度 err = np.float32(r_ui - self.globalMean - bu[uid] - bi[iid] - np.dot(v_pu, v_qi)) #得到最新的 v_pu v_qi 参数,去更新 以前的 v_pu += self.alpha * (err * v_qi - self.reg_p * v_pu) v_qi += self.alpha * (err * v_pu - self.reg_q * v_qi) P[uid] = v_pu Q[iid] = v_qi bu[uid] += self.alpha * (err - self.reg_bu * bu[uid]) bi[iid] += self.alpha * (err - self.reg_bi * bi[iid]) error_list.append(err ** 2) print(np.sqrt(np.mean(error_list))) return P, Q, bu, bi def predict(self, uid, iid): if uid not in self.users_ratings.index or iid not in self.items_ratings.index: return self.globalMean p_u = self.P[uid] q_i = self.Q[iid] return self.globalMean + self.bu[uid] + self.bi[iid] + np.dot(p_u, q_i) if __name__ == '__main__': dataset = pd.read_csv("../data/ua.base", sep="\t", header=None, names=["userId", "movieId", "rating", "ts"]) print(dataset[["userId", "movieId", "rating"]]) dataset.groupby("userId").agg([list]) bsvd = BiasSvd(0.02, 0.01, 0.01, 0.01, 0.01, 10, 20) bsvd.fit(dataset[["userId", "movieId", "rating"]]) s = bsvd.Q pass while True: uid = input("uid: ") iid = input("iid: ") print(bsvd.predict(int(uid), int(iid)))



 浙公网安备 33010602011771号
浙公网安备 33010602011771号