拉氏变换和反变换

1 引言

机电控制工程中经常要解算一些线性微分方程，按照一般方法解算比较麻烦。

如果用拉氏变换求解线性微分方程，可将经典数学中的微积分运算转换为代数运算，又能够单独地表明初始条件的影响，并有变换表可查找，因而是一种较为简便的工程数学方法。更重要的是，采用拉氏变换后，能够把描述系统运动状态的微分方程很方便地转换为系统的传递函数，并由此发展出用传递函数的零极点分布、频率特性等间接地分析和设计控制系统的工程方法。

2 拉氏变换和反变换的定义

2.1 拉氏变换

设函数f(t)(t≥0)在任一有限区间上分段连续，且存在一正实数σ，使得：

则函数f(t)的拉氏变换存在，并定义为：

式中，s=σ+jω(σ、ω均为实数)为复变数。

F(s)称为函数f(t)的拉氏变换或象函数，是一个复变函数，f(t)称为F(s)的原函数。

2.2 拉氏反变换

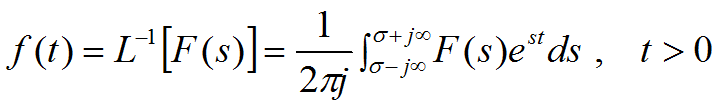
式中，L^-1为拉氏反变换符号。

拉氏变换是描述分析连续、线性、时不变系统的重要工具。

3 简单函数的拉氏变换

3.1 单位阶跃函数1(t)

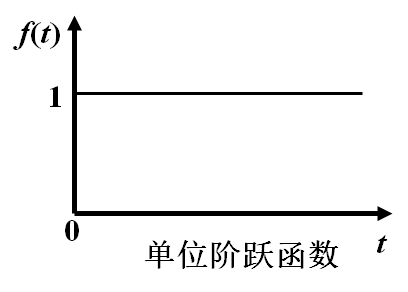
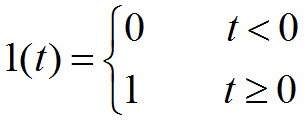
拉氏变换为：

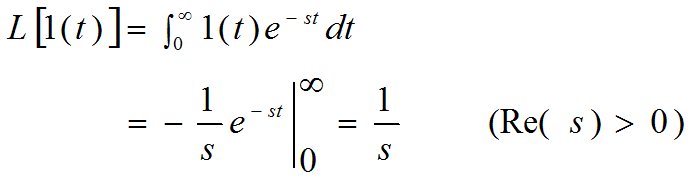
3.2 指数函数

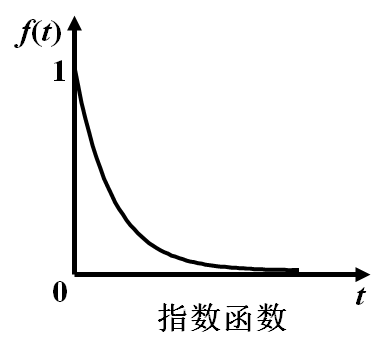
拉氏变换为：

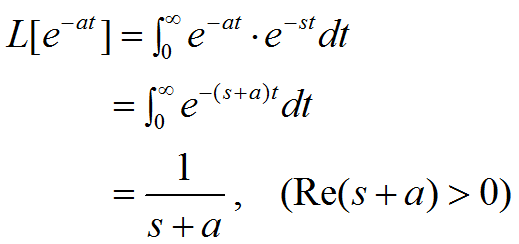
3.3 正弦及余弦函数

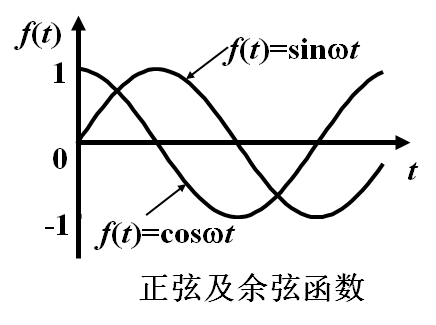
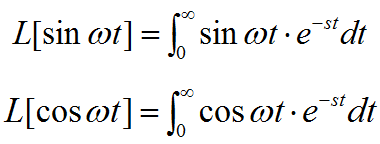
由欧拉公式：

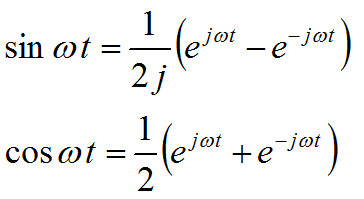
拉氏变换为：

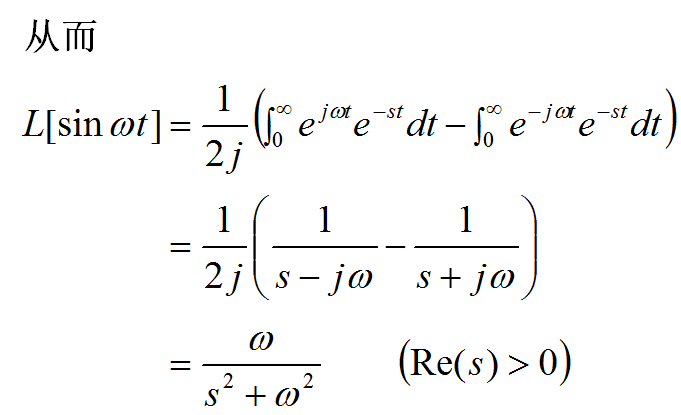
3.4 单位脉冲函数

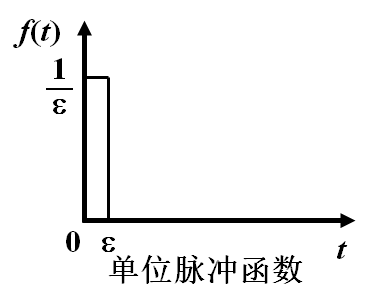
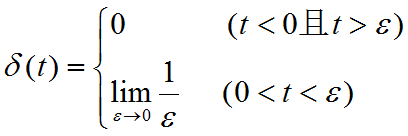
拉氏变换为：

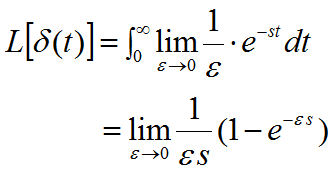
由洛必达法则：

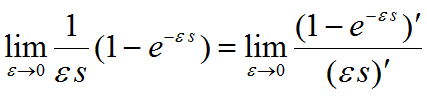
即：

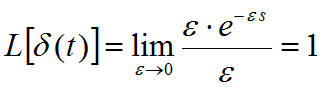
3.5 单位速度函数

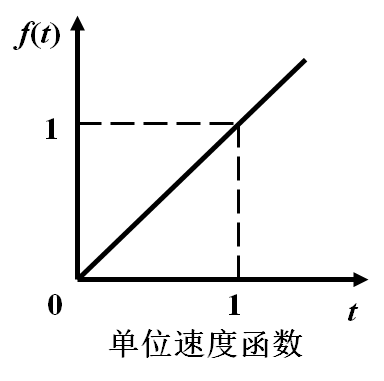
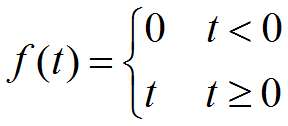
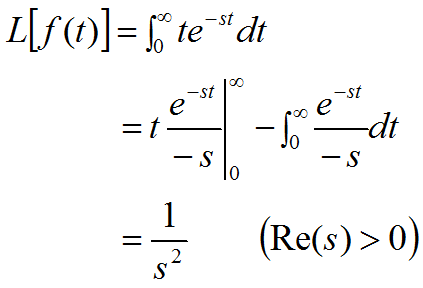
3.6 单位加速度函数

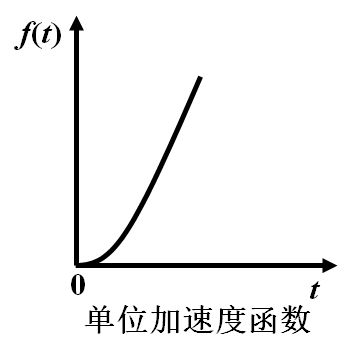
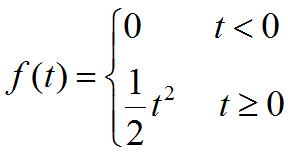
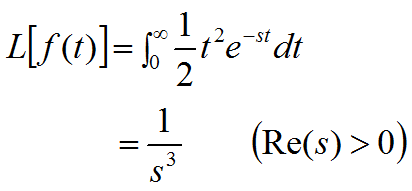
3.7 幂函数

可以利用Γ-函数的性质：

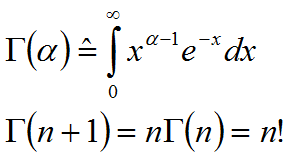
令u=st，则：

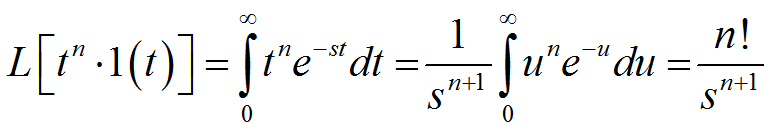
3.8 拉氏变换积分下限的说明

在某些情况下，函数f(t)在t=0处有一个脉冲函数。这时必须明确拉氏变换的积分下限是0^-还是0⁺，并相应记为：

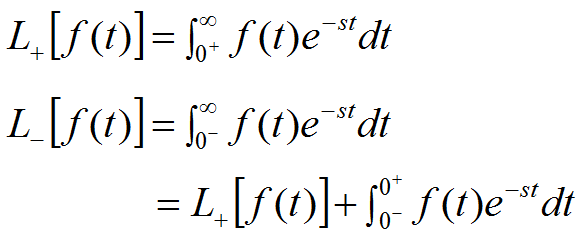
4 拉氏变换性质

4.1 叠加定理

显然，拉氏变换为线性变换。

4.2 微分定理

推论：

当f(t)及其各阶导数在t=0时刻的值均为零时（零初始条件）：

当f(t)在t=0处具有间断点时，df(t)/dt在t=0处将包含一个脉冲函数，即：

当f(0⁺)≠f(0^-)时，则有：

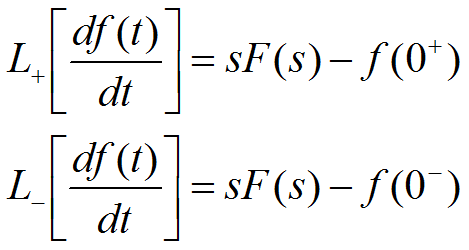
4.3 复微分定理

若L[f(t)]=F(s)，则除了F(s)的极点之外，有：

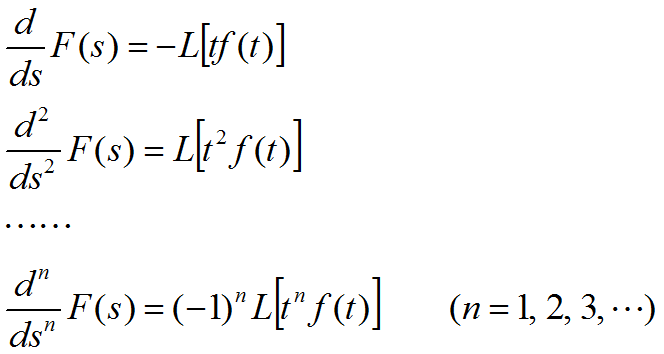
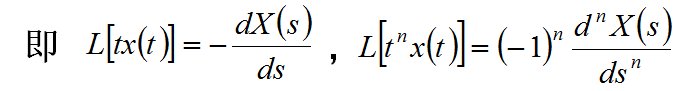
4.4 积分定理

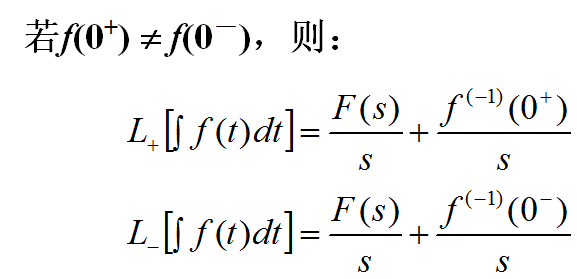
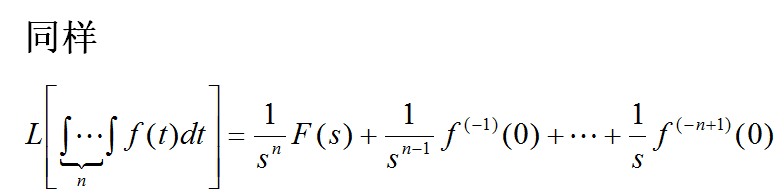
当初始条件为零时：

 

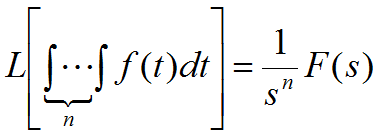
4.5 延时定理

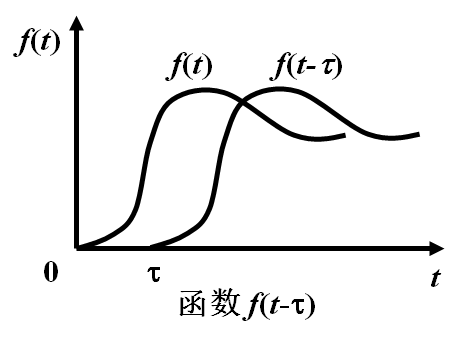
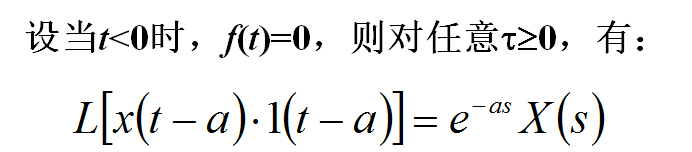
4.6 衰减定理

 

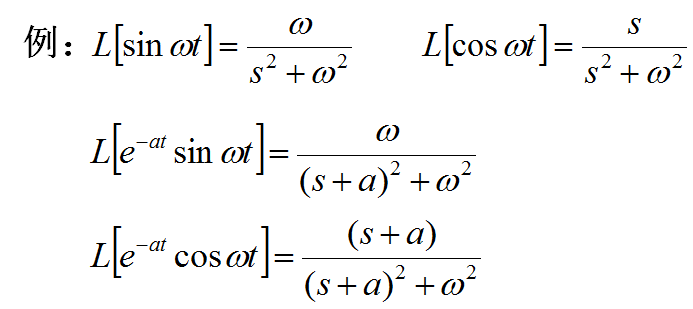
4.7 初值定理

4.8 终值定理

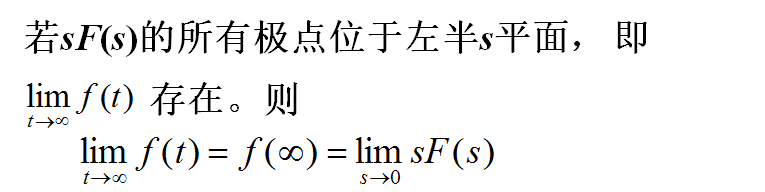
4.9 卷积定理

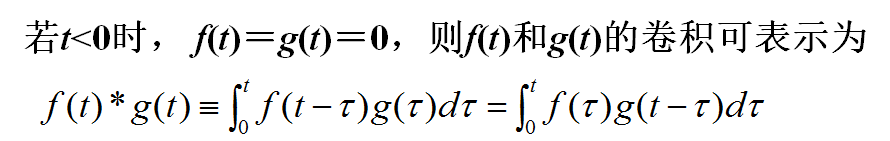
4.10 f(t/a)的象函数

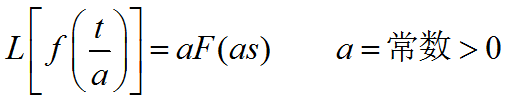
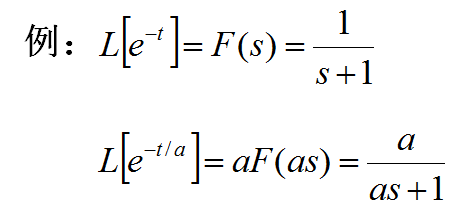
5 拉氏反变换