斯坦福机器学习视频笔记 Week8 无监督学习：聚类与数据降维 Clusting & Dimensionality Reduction

监督学习算法需要标记的样本（x，y），但是无监督学习算法只需要input（x）。 您将了解聚类 - 用于市场分割，文本摘要，以及许多其他应用程序。

Principal Components Analysis, 经常用于加快学习算法，同时对于数据可视化以帮助你对数据的理解也有很大的帮助。

Unsupervised learning Introduction

supervised learning：在前面几课我们学习的都是属于监督性学习的内容，包括回归和分类，主要特点就是我们使用的数据集都是类似(x,y)这种样本，在算法中需要使用x作为训练的输入，然后把y作为分类的lable或输出的数值（在回归中）。

unsupervised learning：这是我们下面着重讨论的。如果要理解其和supervised learning的区别，主要把握一点：在算法训练中我们是否会使用y，当然我们也可以使用类似(x,y)的数据集，但是其中的y我们只是用来做结果验证，不用来训练算法，这一点很重要。

下面是unsupervised learning的应用举例：

K-means algorithm

根据Ng老师的上课顺序，先来看一个K-means 聚类的例子： 

 

开始正式讲解。

 

 

 算法输入：K，需要分类的数量；训练数据集X，去除x0 =1.

下面是算法描述：

 

总体来说，先随机初始化聚类中心centoids u1，u2，...,uk，然后重复迭代下面两步：

1.Cluster assignment：将样本点x(i)分配到离它最近的聚类中心K(距离由欧式距离来衡量，为上面画框的公式)，将它此时分配的簇类型记为c(i),c(i)取值为簇的类标号。

2.Move centroid：根据上一步样本点的分配结果，重新计算聚类中心uk，uk为所有分配点的平均值。比如：现有x(1),x(3),x(5),x(10)，分配给了类标号为2的簇，则簇中心(聚类中心)u2就等于这四个点的均值，如上面的计算。

K-means optimization objective

这里的最优化目标函数J（c，u）是所有样本点离簇中心的距离之和，这里需要弄清楚这些notation的含义。

c(i):x(i)分配给最近簇中心的类标号；

uk：聚类中心k，也就是簇中心，是一个意思。

uc(i):被分配给x（i）的簇中心，这个值可能每次迭代会根据簇中心的变化而变化，比如在这一次迭代中，x(i)被分配到2类簇，可能下次会被分配到4类簇，这样uc(i)就先是u2，然后是u4.

让我们再来回顾一下之前给出的算法：

这里需要说明的是，当执行Cluster assignment的时候，是固定簇中心u不变，最小化J（c，u）来求参数c；

然后Move centroid的时候，是固定c不变，最小化J（c，u）来求参数u。

这个过程个人感觉和最大期望算法(EM)的思想类似，感兴趣的童鞋可以去看看EM算法。

Random initialization

 现在来接着讨论初始化簇中心的问题。

 

随机选择K个训练样本(K<m)，作为簇中心。当然，可能我们运气并不好而选到了上面方框中的两个点，或者我们选择的中心会出现类似下面局部最优的情况，

为避免出现这种情况，通常需要多次初始化簇中心，可以是50～1000次，然后选取使J（c，u）最小的簇中心。

Choosing the number of clusters

老师介绍了一种叫 ’Elbow method‘ 的方法，如下

方法就是以K和J(c,u)作图，当然，在使用的时候，你可能会遇到上面两种情况：

如果出现左边的图，你就应该很兴奋了，这就是所谓的手肘型"Elbow",因为你可以一眼就看出你的最佳的K取值，就是3左右，因为在3之前，J下降的很快，而3之后J下降的不明显。

但如果不幸出现右边的图，可能就不是那么明显了。这时就是“仁者见仁”了。

像这个关于T恤尺码的问题，根据你的实际需要，可以选择3个簇“S,M,L”，也可以选择5个簇"XS,S,M,L,XL"等。

 Dimensionality Reduction

数据降维可以压缩数据，比如对图片的压缩保存，可以节省磁盘空间，另外数据降维可以提高算法的训练速度，还可以用数据降维到2维或者3维进行数据可视化。

Principal Component Analysis problem formulation

 

 

简单的说，数据降维就是用低维度的数据尽量保持原维度的数据表示。

从上面的数据可视化看出，左边的2维图的样本点分布趋势基本在一条直线上，而右边的三维样本点基本分布在2维平面上，所以我们可以分别用一维和二维数据来表示上面的数据分布。

数据降维的关键就是找到数据投影的方向，使样本x在该方向上的projection error最小。以二维数据为例：

将上面两幅图做一下对比，你觉得应该选择哪一个投影方向比较适合？当然是第二个。

为什么？之前讨论的数据降维的目标是：使用低维的数据尽量保持或表示出原数据的特征。

观察上面数据的分布特征，可以看出数据大体是沿正向45度角分布的，我们做投影时，应该使数据的投影尽量的区分开，不能像左图那样太集中，而是像右图那样分散开，这样也得到了最小的projection error 。

然后我们就用样本在该方向的投影值来表示原来的数据，就达到了压缩的目的。

有同学会发现这怎么和前面讲的回归很类似，下面讲讲他们之间的区别：

1.回归是supervised learning，而PCA是Unsupervised learning，即PCA不需要使用样本的y；

2. PCA衡量的是orthogonal distance, 而linear regression是所有x点对应的真实值y与估计值h(x)之间的vertical distance距离。可以在上图看到，第一个是回归，这个error是x真实的y值与预测值之间的垂直距离，而PCA的error是x与其在投影方向的垂直距离。

Principal Component Analysis algorithm 

数据预处理：feature scaling/mean normalization

Reduce data from n-dimensions to k-dimensions

计算协方差矩阵Sigma：

计算特征向量U：

在Octive/Matlab中使用函数svd，进行“奇异值分解”（singular value decomposition）求解特征向量U。

我们需要选择K个最大特征值对应的特征向量。

使用SVD函数求得的U中，已经自动排好序列，选择前K个向量，作为我们数据投影的“基向量”：

然后将x表示成压缩后的新样本z：z=Ureduce‘ * x;其中x是n维，z是压缩后的k维。

给出对上面内容的总结：

Reconstruction from compressed representation

我们使用Z = Ureduce ’ * x 将数据压缩到k维，现在我们也可以通过Xapprox = Ureduce * Z 将数据还原成类似原来的样子，但是请注意，这个还原的Xapprox是我们对原数据的估计，是有误差的，不可能回到和原来一模一样的情况，所以这个就要求我们在压缩的时候压缩维度的情况下尽可能保持数据的原始特征。从上面的图可以看出，我们还原出来的数据和原数据的差别。

 choosing the number of principal components k

为了选择最佳的principal components 的K值，我们使用方框中的公式来定量评估压缩后的数据对原来数据特性（ariance）的保持度。

设置一个阈值，比如10%，当公式的结果值在阈值以内我们就认为这个K值的压缩结果是可以接受的。

那我们的PCA算法就是这样的：

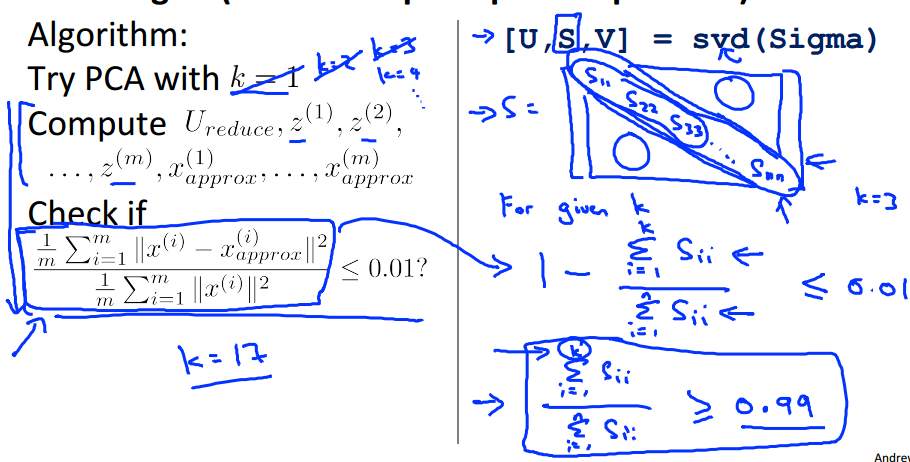
对于不同的K=1，K=2......，从小到大这么取K值，然后计算它的Ureduce(K个特征向量) ，Z(压缩后的数据表示)，和Xapprox(还原后的近似数据)，计算上面的公式是否在你设置的阈值以内，取最小的满足阈值的K值作为理想的principal components的数量。这里需要说明的是，我们在svd函数求出的返回值中包含一个S矩阵，可以用它来计算判别式的值。S是一个对角矩阵，由Sigma的特征值组成，直接可以用

前k个特征值的和/特征值的总和  来计算，看上面的例子。

Application of PCA 

1.使用PCA提高监督性学习的训练速度。先使用没有标记的数据X，经过PCA处理得到新的数据Z，将新的数据集（Z，y）用于算法训练。PCA不仅可以运用在training set，还可以在Xcv和Xtest中使用。

2.数据压缩和数据可视化。

3.不要使用PCA来防止过拟合，而是应该使用regulrization。

Note：

在设计机器学习算法时，不要首先就考虑要使用PCA,当你在原始数据训练结果不理想时，再考虑使用PCA.

 

参考：http://blog.csdn.net/abcjennifer/article/details/8002329