实验九
学号 2019-2020-1823 《数据结构与面向对象程序设计》实验六报告
班级: 1823
姓名: 杨凯涵
学号:20182321
实验教师:王志强
实验日期:2019年10月22日
必修/选修: 必修
1.实验内容
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
PS:本题12分。目前没有明确指明图的顶点和连通边,如果雷同或抄袭,本次实验0分。
2实验过程及结果
实验一
初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
首先我们现在稿纸上设计好要花的图
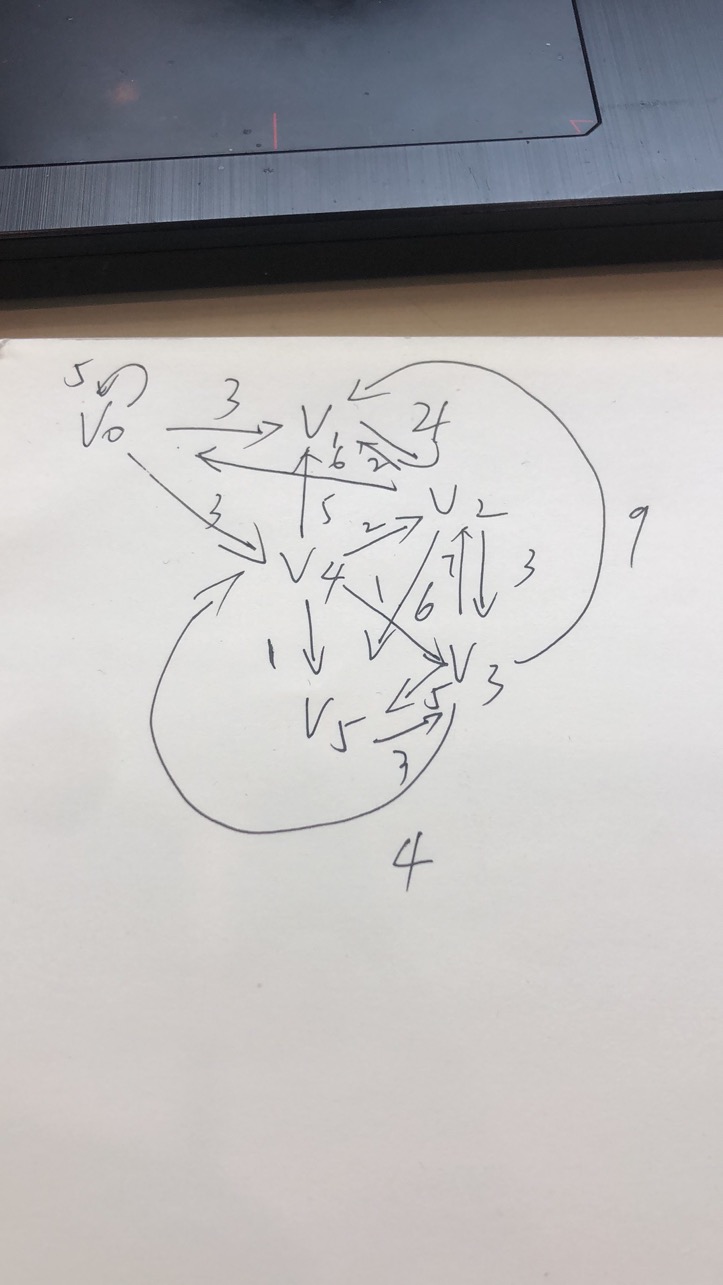
接着,我们开始初始化图,以下为主程序的代码(初始化图的代码与之前的周总结内容和实验相同,再次不做过多论述)
Vertex a = main.new Vertex("V0",0);//0到第一个节点的最短路径设置为0
Vertex b = main.new Vertex("V1");
Vertex c = main.new Vertex("V2");
Vertex d = main.new Vertex("V3");
Vertex e = main.new Vertex("V4");
Vertex f = main.new Vertex("V5");
vertexs.add(a);
vertexs.add(b);
vertexs.add(c);
vertexs.add(d);
vertexs.add(e);
vertexs.add(f);
int[][] edges = {
{5,3,Integer.MAX_VALUE,Integer.MAX_VALUE,3,Integer.MAX_VALUE},
{Integer.MAX_VALUE,Integer.MAX_VALUE,4,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE},
{6,2,Integer.MAX_VALUE,3,Integer.MAX_VALUE,6},
{Integer.MAX_VALUE,9,7,Integer.MAX_VALUE,4,5},
{Integer.MAX_VALUE,5,2,1,Integer.MAX_VALUE,7},
{Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,3,Integer.MAX_VALUE,Integer.MAX_VALUE}
};
Graph graph = main.new Graph(vertexs, edges);
List<Vertex> vertexs1 = new ArrayList<Vertex>();
Vertex a1 = main.new Vertex("V0",0);//0到第一个节点的最短路径设置为0
Vertex b1 = main.new Vertex("V1");
Vertex c1 = main.new Vertex("V2");
Vertex d1 = main.new Vertex("V3");
Vertex e1 = main.new Vertex("V4");
Vertex f1 = main.new Vertex("V5");
vertexs1.add(a1);
vertexs1.add(b1);
vertexs1.add(c1);
vertexs1.add(d1);
vertexs1.add(e1);
vertexs1.add(f1);
int[][] edges1 = {
{5,3,0,0,3,0},
{0,0,4,0,0,0},
{6,2,0,3,0,6},
{0,9,7,0,4,5},
{0,5,2,1,0,1},
{0,0,0,3,0,0}
};
Graph graph1 = main.new Graph(vertexs1,edges1);
接着输出结果为:
有向图
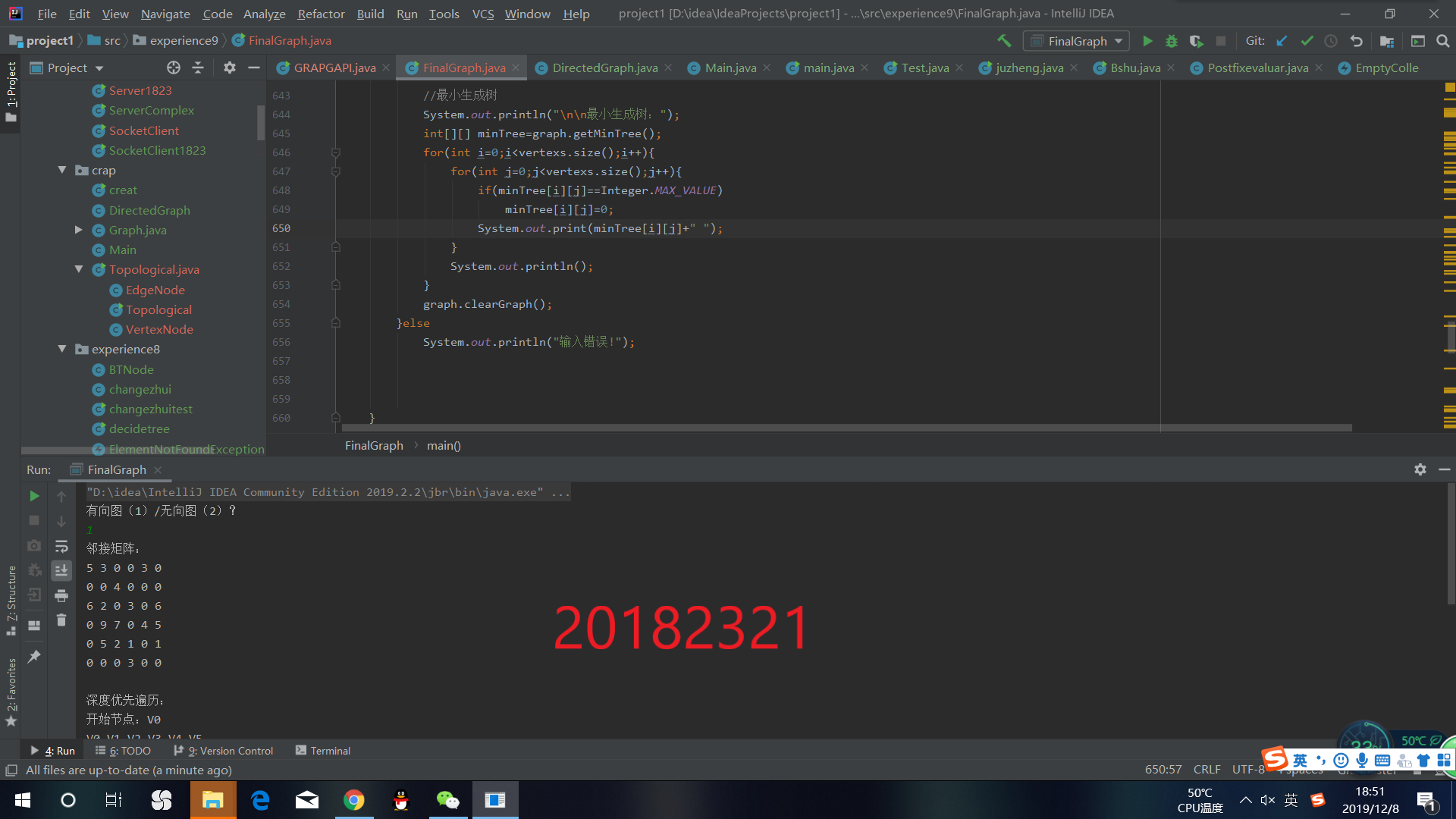
无向图

实验二
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
有向图和无向图的深度遍历和广度遍历的核心代码为
深度遍历
public void DFS(String vertexName){
int id=getIdOfVertexName(vertexName);
if(id==-1)return;
vertexs.get(id).setMarked(true);
System.out.print(vertexs.get(id).getName()+" ");
List<Vertex> neighbors = getNeighbors(vertexs.get(id));
for(int i=0;i<neighbors.size();i++){
if(!neighbors.get(i).isMarked()){
DFS(neighbors.get(i).getName());
}
}
}
广度遍历
public void BFS(String vertexName){
int startID=getIdOfVertexName(vertexName);
if(startID==-1) return;
List<Vertex> q=new ArrayList<Vertex>();
q.add(vertexs.get(startID));
vertexs.get(startID).setMarked(true);
while(!q.isEmpty()){
Vertex curVertex=q.get(0);
q.remove(0);
System.out.print(curVertex.getName()+" ");
List<Vertex> neighbors = getNeighbors(curVertex);
for(int i=0;i<neighbors.size();i++){
if(!neighbors.get(i).isMarked()){
neighbors.get(i).setMarked(true);
q.add(neighbors.get(i));
}
}
}
}
运行结果如下

实验三
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
拓扑排序定义: 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若<u,v> ∈E(G),则u在线性序列中出现在v之前。
通常,这样的线性序列称为满足拓扑次序(TopoiSicai Order)的序列,简称拓扑序列。

部分代码
VertexNode v0 = new VertexNode(0, 1, null);
EdgeNode v0e0 = new EdgeNode(1, 0, null);
EdgeNode v0e1 = new EdgeNode(2, 0, null);
v0.setFirstEdge(v0e0);
v0e0.setNext(v0e1);
VertexNode v1 = new VertexNode(0, 1, null);
EdgeNode v1e0 = new EdgeNode(3, 0, null);
EdgeNode v1e1 = new EdgeNode(4, 0, null);
v1.setFirstEdge(v1e0);
v1e0.setNext(v1e1);
VertexNode v2 = new VertexNode(1, 2, null);
EdgeNode v2e0 = new EdgeNode(3, 0, null);
EdgeNode v2e1 = new EdgeNode(5, 0, null);
v2.setFirstEdge(v2e0);
v2e0.setNext(v2e1);
VertexNode v3 = new VertexNode(2, 3, null);
EdgeNode v3e0 = new EdgeNode(5, 0, null);
运行结果

实验四
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
求最小生成树的方法由下面的图来演示
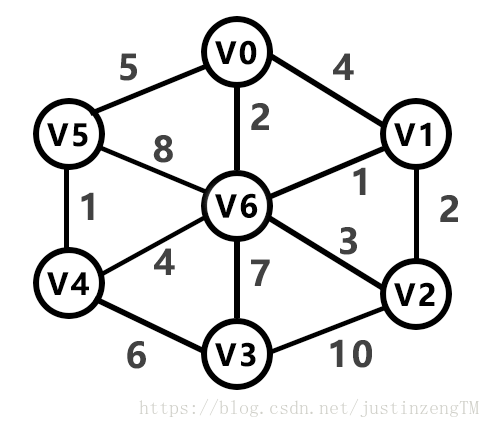

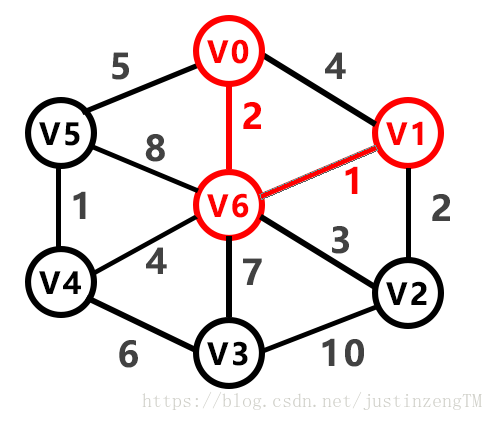
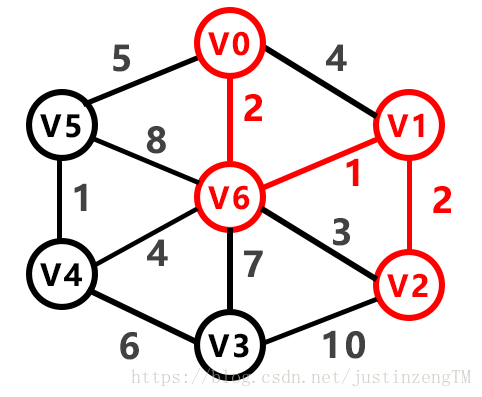
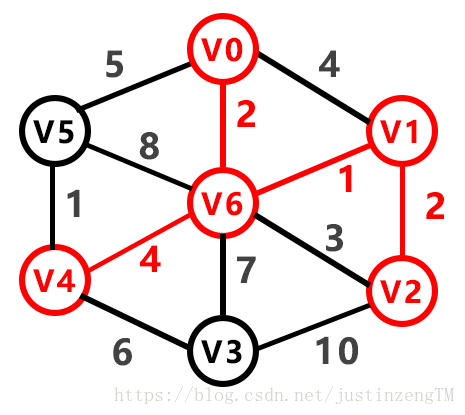
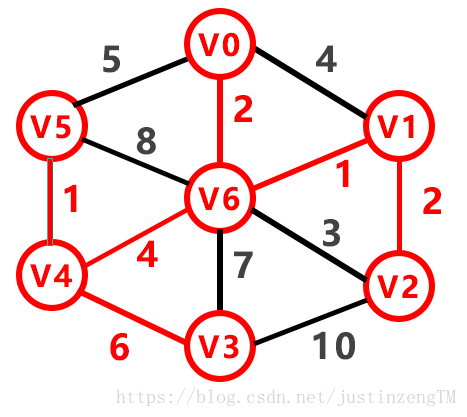
通过以上的算法,我们的实现代码为
for(int i=0;i<vertexs.size();i++){
if(vertexs.get(i).getAnotherIDinminEdge()!=-1){
minTree[getIdOfVertexName(vertexs.get(i).getName())][vertexs.get(i).getAnotherIDinminEdge()]=
edges[getIdOfVertexName(vertexs.get(i).getName())][vertexs.get(i).getAnotherIDinminEdge()];
minTree[vertexs.get(i).getAnotherIDinminEdge()][getIdOfVertexName(vertexs.get(i).getName())]=
edges[vertexs.get(i).getAnotherIDinminEdge()][getIdOfVertexName(vertexs.get(i).getName())];
}
}//设置生成最小生成树
for(int i=0;i<this.vertexs.size();i++){
for(int j=0;j<this.vertexs.size();j++){
this.minTree[i][j]=Integer.MAX_VALUE;
}//初始化最小生成树
initMinTree();//初始化最小生成树
while(!allVisited()){
Vertex vertex = vertexs.get(getNotMarkedMinVertex());//设置处理节点
//System.out.println("处理:节点"+vertex.getName());
//顶点已经计算出最短路径,设置为"已访问"
vertex.setMarked(true);
//获取所有"未访问"的邻居
List<Vertex> neighbors = getNeighbors(vertex);
//System.out.println("邻居个数为:"+neighbors.size());
//更新最小生成树
updateMinEdge(vertex, neighbors);
}
//System.out.println("search over");
setMinTree();
return minTree;//获得最小生成树
public void updateMinEdge(Vertex vertex, List<Vertex> neighbors){
//参数检测
if(!isInGraph(vertex)){
System.out.println("当前节点不在图中");
return ;
}
for(Vertex neighbor: neighbors){
int distance = edges[getIdOfVertexName(neighbor.getName())][getIdOfVertexName(vertex.getName())];
if(neighbor.getAnotherIDinminEdge()==-1){
neighbor.setAnotherIDinminEdge(getIdOfVertexName(vertex.getName()));
//System.out.println(neighbor.getName()+" setEdge To "+vertex.getName()+edges[neighbor.getAnotherIDinminEdge()][getIdOfVertexName(neighbor.getName())]);
}
else if(distance < edges[getIdOfVertexName(neighbor.getName())][neighbor.getAnotherIDinminEdge()]){
neighbor.setAnotherIDinminEdge(getIdOfVertexName(vertex.getName()));
//System.out.println(neighbor.getName()+" setEdge To "+vertex.getName()+edges[neighbor.getAnotherIDinminEdge()][getIdOfVertexName(neighbor.getName())]);
}
}
}//更新最小生成树
实验五
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。在弄清楚如何求算单源最短路径问题之前,必须弄清楚最短路径的最优子结构性质。
一.最短路径的最优子结构性质
该性质描述为:如果P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,k和s是这条路径上的一个中间顶点,那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。
假设P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径P'(k,s),那么P'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。
二.Dijkstra算法
由上述性质可知,如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。譬如对于源顶点V0,首先选择其直接相邻的顶点中长度最短的顶点Vi,那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。根据这种思路,
假设存在G=<V,E>,源顶点为V0,U={V0},dist[i]记录V0到i的最短距离,path[i]记录从V0到i路径上的i前面的一个顶点。
1.从V-U中选择使dist[i]值最小的顶点i,将i加入到U中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+matrix[i][j]})
3.知道U=V,停止。
代码如下
/**
* 搜索各顶点最短路径
*/
public void search(){
while(!unVisited.isEmpty()){
Vertex vertex = unVisited.element();
//顶点已经计算出最短路径,设置为"已访问"
vertex.setMarked(true);
//获取所有"未访问"的邻居
List<Vertex> neighbors = getNeighbors(vertex);
//更新邻居的最短路径
updatesDistance(vertex, neighbors);
pop();
}
System.out.println("最短路径");
}
/**
* 获取顶点到目标顶点的距离
*/
private int getDistance(Vertex source, Vertex destination) {
if(!isInGraph(source)||!isInGraph(destination)){
System.out.println("当前节点不在图中");
return -1;
}
/**
* 获取顶点所有(未访问的)邻居
*/
public List<Vertex> getNeighbors(Vertex v) {
//参数检测
if(!isInGraph(v)){
System.out.println("当前节点不在图中");
return null;
}
List<Vertex> neighbors = new ArrayList<Vertex>();
int position = vertexs.indexOf(v);
Vertex neighbor = null;
int distance;
for (int i = 0; i < vertexs.size(); i++) {
if (i == position) {
//顶点本身,跳过
continue;
}
distance = edges[position][i]; //到所有顶点的距离
if (distance < Integer.MAX_VALUE) {
//是邻居(有路径可达)
neighbor = getVertex(i);
if (!neighbor.isMarked()) {
//如果邻居没有访问过,则加入list;
neighbors.add(neighbor);
}
}
}
return neighbors;
}
/**
* 根据顶点位置获取顶点
*/
private Vertex getVertex(int index) {
if(index<0||index>vertexs.size()+1){
System.out.println("获取ID为"+index+"失败");
return null;
}
return vertexs.get(index);
}
运行结果如图
3. 实验过程中遇到的问题和解决过程
- 问题1:实现迪杰斯特拉算法
- 问题1解决方法:
一、算法思想
Dijkstra算法是最短路径算法中为人熟知的一种,是单起点全路径算法。该算法被称为是“贪心算法”的成功典范。
1、令G = (V,E)为一个带权无向图。G中若有两个相邻的节点,i和j。aij(在这及其后面都表示为下标,请注意)为节点i到节点j的权值,在本算法可以理解为距离。每个节点都有一个值di(节点标记)表示其从起点到它的某条路的距离。
2、算法初始有一个数组V用于储存未访问节点的列表,我们暂称为候选列表。选定节点1为起始节点。开始时,节点1的d1=0, 其他节点di=无穷大,V为所有节点。
初始化条件后,然后开始迭代算法,直到V为空集时停止。具体迭代步骤如下:
将d值最小的节点di从候选列表中移除。(本例中V的数据结构采用的是优先队列实现最小值出列,最好使用斐波那契对,在以前文章有过介绍,性能有大幅提示)。对于以该节点为起点的每一条边,不包括移除V的节点, (i, j)属于A, 若dj > di + aij(违反松弛条件),则令
dj = di + aij , (如果j已经从V中移除过,说明其最小距离已经计算出,不参与此次计算)
可以看到在算法的运算工程中,节点的d值是单调不增的。
代码如下
public class Dijkstra {
class Item
{ String endString;
ArrayList<String>lujingArrayList=new ArrayList<String>();
int distance;
}
public void GetShortWay(Graph graph,String startpoint,String endpoint) {
int startindex=graph.vertexList.indexOf(startpoint);
ArrayList<Item>Sarray=new ArrayList<Dijkstra.Item>();//S列表中存已知最短路径的对象,U列表中存未知最短路径的对象
ArrayList<Item>Uarray=new ArrayList<Dijkstra.Item>();//S列表中存已知最短路径的对象,U列表中存未知最短路径的对象
//初始化U列表
for(int i=0;i<graph.getNumofVertex();i++)
{
Item tempItem=new Item();
tempItem.endString=graph.vertexList.get(i);
tempItem.lujingArrayList.add(graph.vertexList.get(startindex));
tempItem.lujingArrayList.add(graph.vertexList.get(i));
tempItem.distance=graph.edges[startindex][i];
Uarray.add(tempItem);
}
while (!Uarray.isEmpty()) {
int t=0;
int tempdistance=Uarray.get(0).distance;
for(int i=0;i<Uarray.size();i++)
{
if(tempdistance>Uarray.get(i).distance)
{
t=i;
tempdistance=Uarray.get(i).distance;
}
}
Sarray.add(Uarray.remove(t));
for(int i=0;i<Uarray.size();i++)
{
int index1=graph.vertexList.indexOf(Uarray.get(i).endString);
for(int j=0;j<Sarray.size();j++)
{
int index2=graph.vertexList.indexOf(Sarray.get(j).lujingArrayList.get(Sarray.get(j).lujingArrayList.size()-1));
if(graph.edges[index1][index2]==Integer.MAX_VALUE)
{
continue;
}
else {
int newdistance=Sarray.get(j).distance+graph.edges[index1][index2];
if(newdistance<Uarray.get(i).distance)
{
Uarray.get(i).distance=newdistance;
Uarray.get(i).lujingArrayList=new ArrayList<String>( Sarray.get(j).lujingArrayList);
Uarray.get(i).lujingArrayList.add(graph.vertexList.get(index1));
}
}
}
}
}
for(int i=0;i<Sarray.size();i++)
{
System.out.print( startpoint+"-->"+Sarray.get(i).endString+"的最短路径为:");
for(int j=0;j<Sarray.get(i).lujingArrayList.size();j++)
{System.out.print( Sarray.get(i).lujingArrayList.get(j)+" ");}
System.out.println("长度为:"+ Sarray.get(i).distance);
}
}
}
- 问题2:如何代码打出广度遍历和深度遍历
- 问题2解决方法:
在上面的基础上,我们进行编写广度遍历和深度遍历的方法,这两个方法用到了堆栈的方式来实现,以下给出代码
深度遍历
public String DFS(String startnode,ArrayList<String> vertexList,int [][]edges) {
if (!vertexList.contains(startnode)) {
System.out.print("输入节点不在该图内");
return null;
}
int startindex=vertexList.indexOf(startnode);
int numOfNodes=vertexList.size();
boolean[]visted=new boolean[numOfNodes];
StringBuilder resultBuilder=new StringBuilder();
Stack<Integer> stack=new Stack<Integer>();
stack.push(startindex);
visted[startindex]=true;
while (!stack.isEmpty()) {
int v=stack.pop();
resultBuilder.append(vertexList.get(v)+",");
for(int i=0;i<numOfNodes;i++)
{
//当edges【v】【i】的值不为0,不为最大,且没有被访问时,将其压入栈中
if((edges[v][i]!=0)&&(edges[v][i]!=Integer.MAX_VALUE)&&!visted[i])
{
stack.push(i);
visted[i]=true;
}
}
}
return resultBuilder.length()>0?resultBuilder.substring(0,resultBuilder.length()-1):null;
}
广度遍历
public String BFS(String startnode,ArrayList<String> vertexList,int [][]edges) {
if (!vertexList.contains(startnode)) {
System.out.print("输入节点不在该图内");
return null;
}
StringBuilder resultBuilder=new StringBuilder();
boolean []visited=new boolean[vertexList.size()];
int startIndex=vertexList.indexOf(startnode);
Queue<Integer>queue=new LinkedList<Integer>();
queue.offer(startIndex);
visited[startIndex]=true;
while (!queue.isEmpty()) {
int v=queue.poll();
resultBuilder.append(vertexList.get(v)+",");
for(int i=0;i<vertexList.size();i++)
{
if((edges[v][i]!=0) &&( edges[v][i]!=Integer.MAX_VALUE)&&!visited[i])
{
queue.offer(i);
visited[i]=true;
}
}
}
return resultBuilder.length()>0?resultBuilder.substring(0,resultBuilder.length()-1):null;
}
其他(感悟、思考等)
- 很高兴能圆满完成这学期的所有实验,感悟最深的不是学了多少的数据结构、多少的java算法、多少的关于安卓、关于java的各种各样的知识,是感觉自己自学能力的提高,自己对于解决苦难的能力的提高,在困境中的不懈努力和寻求解决难题的方法,才是我觉得这门课给我最多的东西
- 完成这个实验后还有这最后一个难度最大的app在等着我们,加油!
参考资料
《Java程序设计与数据结构教程(第二版)》
《Java程序设计与数据结构教程(第二版)》学习指导




