20162302 《程序设计与数据结构》第十一周学习总结

20162302 2017-2018-1 《程序设计与数据结构》第十一周学习总结

教材学习内容总结

掌握Hash 函数的实现
理解哈希表中的冲突问题
分析Java Collection API中的Hash 实现

教材学习中的问题和解决过程

  • 问题：什么是哈希函数

  • 哈希函数（英语：Hash Function）是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要，使得数据量变小，将数据的格式固定下来。该函数将数据打乱混合，重新创建一个叫做散列值的指纹。散列值通常用来代表一个短的随机字母和数字组成的字符串。好的散列函数在输入域中很少出现散列冲突。在散列表和数据处理中，不抑制冲突来区别数据，会使得数据库记录更难找到。（节选自搜狗百科哈希函数）

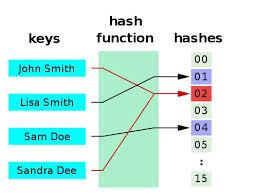
  • 问题：什么是冲突问题

  • 书上的例子是这样子的：

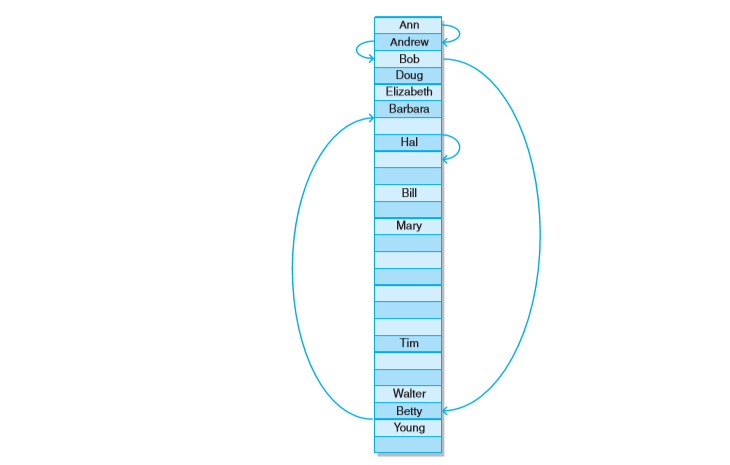
创建一个包含26个元素的数组来保存名字，为此建立一个哈希函数，每个名字位于的位置等于名字的首字母，当同时保存“Ann”和“Andrew”的时候会出现两个关键字映射到一个位置，这种现象就是冲突。

无论哈希函数设计有多么精细，都会产生冲突现象，也就是2个关键字处理函数的结果映射在了同一位置上，因此，有一些方法可以避免冲突。（节选自搜狗百科哈希函数）

  • 问题：解决冲突的问题有哪些？
  • 解决冲突的方法：
    1、链式方法（又称拉链方法）
    将哈希表看成是集合的表而不是个独立单元的表。所以每个单元中保存一个指针，指向与表中该位置相关的元素的集合。通常表内的这些集合既没有先后次序也没有大小次序。
    有多种实现方法：
    （1）令保存表的数组大于存储数据的表的大小，利用额外的空间作为溢出区来保存与每个表位置对应的链表。

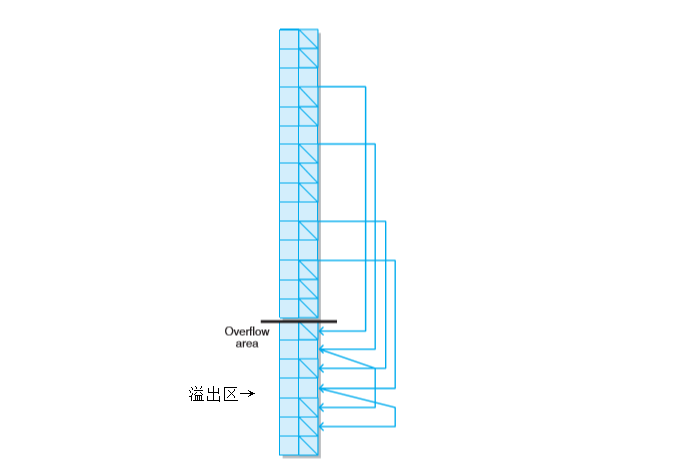
    （2）使用链的方法，将元素映射到桶里面。

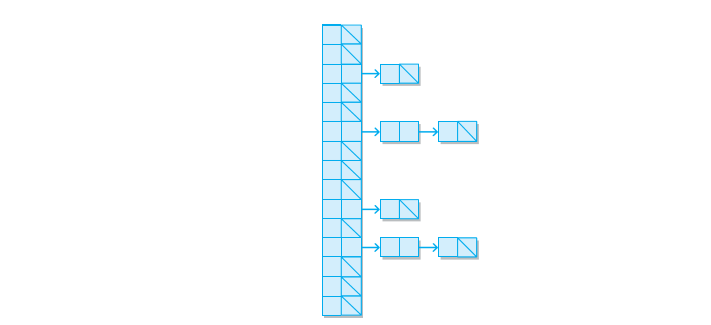
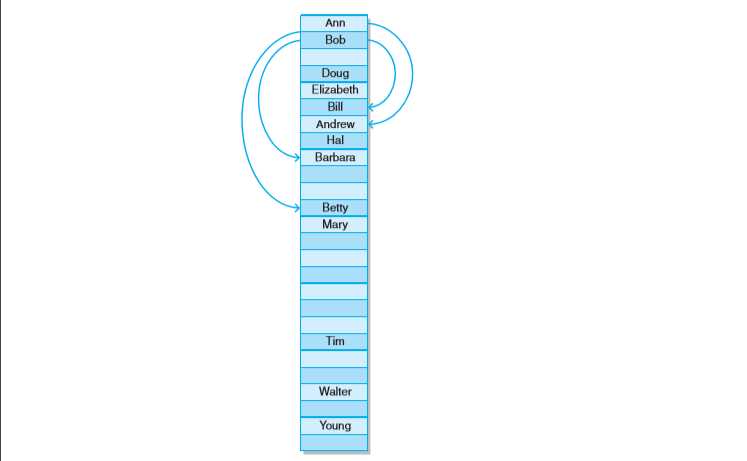
2、开放地址方法
在表中寻找不同于该元素原先哈希到的另一个开放的位置。有多种方法可以查找到表中可用的另一个位置。
（1）线性探测：直接在表中按顺序插入数据，常常让表中已经填充的数据进行聚集。

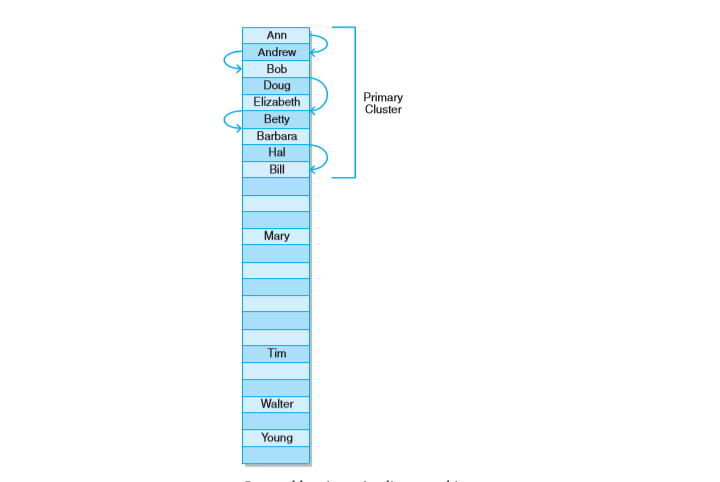
（2）二次探测：

（3）双哈希方法：

代码调试中的问题和解决过程

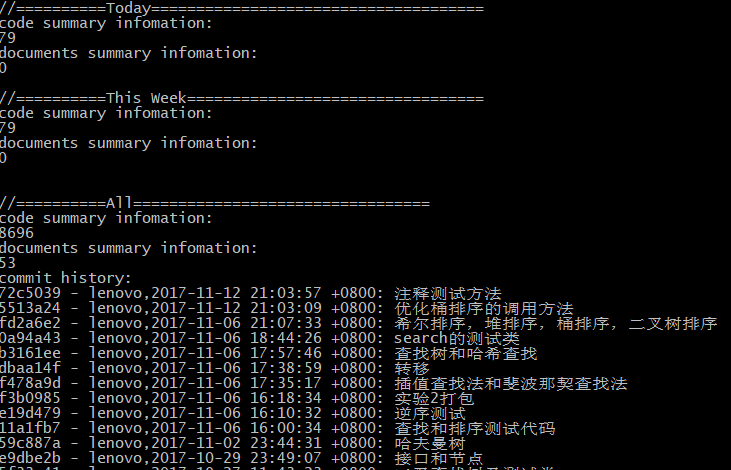
代码托管

上周考试错题总结

  • 错题1：In a binary search tree, the elements in the left subtree of the root are D the root element.
    A.greater than
    B.less than
    C.greater than or equal to
    D.less than or equal to
    E.equal to
    解析：The elements in the left subtree of the root are less than the root element.（在二叉查找树中根的左子树中的元素小于或等于根元素。）
  • 错题2：When adding a new element to a binary search tree, the element is added as a(n) C
    A.internal node
    B.subtree
    C.leaf
    D.root
    E.none of the above
    解析：An element added to a binary search tree is added as a leaf.（将一个元素作为一个叶子添加到二进制搜索树。）
  • 问题3：When removing an element from a binary search tree that is a leaf, _C_will ensure that the resulting tree is still a binary search tree.
    A.replacing it with its only child
    B.replacing it with its inorder successor
    C.simply deleting it
    D.all of the above
    E.neither a, b, nor c
    解析：If the element that we wish to remove is a leaf, then simply deleting it will ensure that the resulting tree is still a binary search tree.（如果我们希望删除的元素是一个叶，那么简单地删除它可以确保生成的树仍然是一个二进制搜索树。）
  • 问题4：In the worst case, a general binary search tree could require _B_comparisons to find an element.
    A.O(1)
    B.O(n)
    C.O(2n)
    D.O(log2 n)
    E.none of the above
    解析：If the elements of a binary search tree are inserted in increasing or decreasing order, then finding an element will require a number of comparisons that is linear in the number of elements.（如果二进制搜索树的元素是在升序或降序中插入的，那么找到一个元素将需要一个在元素数中线性的比较数。）
  • 问题5：If a binary search tree becomes unbalanced after an element is added, it is sometimes possible to efficiently rebalance the tree by A .
    A.using left and right rotations
    B.selecting a leaf node to use as a new root
    C.reconstructing the tree from scratch
    D.all of the above
    E.it is impossible to rebalance a tree efficiently
    解析：Left and right rotations are useful in rebalancing a tree.（左旋和右旋转有助于重新平衡树。）

结对及互评

  • 博客中值得学习的或问题：
    • 叙述的问题很清晰，讲解很仔细
    • 结构清晰

本周结对学习情况

  • 20162329

  • 结对学习内容：
    没有进行系统的结对学习

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 0/0 1/1 10/10
第二周 ??/?? 1/2 15/25
第三周 465/465 1/3 15/40
第五&六周 443/908 3/7 40/80
第七周 528/1436 2/9 20/100
第八周 881/2317 2/11 15/115
第九周 936/3253 1/12 20/135
第十周 628/3881 2/14 20/155
第十一周 79/3960 1/15 15/160

参考资料

posted @ 2017-11-19 22:51  20162302  阅读(172)  评论(0)  编辑  收藏  举报