20162302 实验二《树》实验报告
实 验 报 告
课程:程序设计与数据结构
姓名:杨京典
班级:1623
学号:20162302
实验名称:树
实验器材:装有IdeaU的联想拯救者15ISK
实验目的与要求:
1.实现二叉树
2.中序先序序列构造二叉树
3.决策树
4.表达式树
5.二叉查找树
6.红黑树分析
实验内容、步骤与体会:
实验内容:
实现二叉树
LinkedBinaryTree
书上已给出接口BinaryTree,这项实验目的是补全书上的链树LinkedBinaryTree。然后实现getRight,contains,toString,preorder,postorder五个方法

- 构建
getRight方法:书上已给出getLeft方法,也是在判断跟不为空的情况下建立一个新的LinkedBinaryTree来盛放获取的跟的右子树,并返回这个新建立的变量。
public LinkedBinaryTree<T> getRight() {
if (root == null)
throw new EmptyCollectionException ("Get left operation " + "failed. The tree is empty.");
else {
LinkedBinaryTree<T> result = new LinkedBinaryTree<T>();
result.root = root.getRight();
return result;
}
}
- 构建
contains方法:光看方法名是不容易理解它是干什么用的,所以就要翻一下接口
如果二进制树包含与指定元素匹配的元素和false,否则返回true。刚好BTNode里面包含一个查找方法find可以寻找树里面是否包含匹配元素并返回相应元素。所以可以借助find来查找。
public boolean contains(T target) {
if (root.find(target) == null)
return false;
else
return true;
}
- 构建
toString方法:这个方法的选择就很多样化了,可以根据不同的遍历方法打印出来不同的遍历结果。
同时,因为ArrayIterator继承自ArrayList,所以也可以直接以列表的形式打印出来

所以toString方法就可以直接调用层级遍历的返回值。
public String toString() {
return levelorder().toString();
}
- 构建
preorder和postorder方法:这两个方法是先序遍历和后序遍历,课本中已给出中序遍历,我们可以拿来参考
可以看出来什么都看不出来,只是调用了一个方法,这个方法在
BTNode里面,所以就要到BTNode里面去看
可以明显的看出来先访问左子树,然后访问跟,最后访问右子树。
可以类似的写出前序和后序
public void preorder (ArrayIterator<T> iter) {
iter.add (element);
if (left != null)
left.preorder (iter);
if (right != null)
right.preorder (iter);
}
public void postorder (ArrayIterator<T> iter) {
if (left != null)
left.postorder (iter);
if (right != null)
right.postorder (iter);
iter.add (element);
}
- 这里也对于书上的方法进行完善,在调用书上的代码的时候,调用
LinkedBinaryTree("1", null, t2)的时候会出现空指针问题,然而在这里需要加一个判断条件就可以避免空指针的问题。
public LinkedBinaryTree(T element, LinkedBinaryTree<T> left, LinkedBinaryTree<T> right) {
root = new BTNode<T>(element);
if(left==null)
root.setLeft(null);
else
root.setLeft(left.root);
if(right==null)
root.setRight(null);
else
root.setRight(right.root);
}
中序先序序列构造二叉树
PreInoTre
- 参考代码:根据前序和中序序列,建立二叉树(java实现)
以上代码使用了HashMap但是我不知道是什么意思,所以就要查帮助文档

看得一头雾水,但是还是有办法,可以通过百度相对直观的了解一下使用方法HashMap的使用方法详解
决策树
DecisionTree
- 这一部分相对简单,书上也有相应的代码,这个重点是要写清条件关系
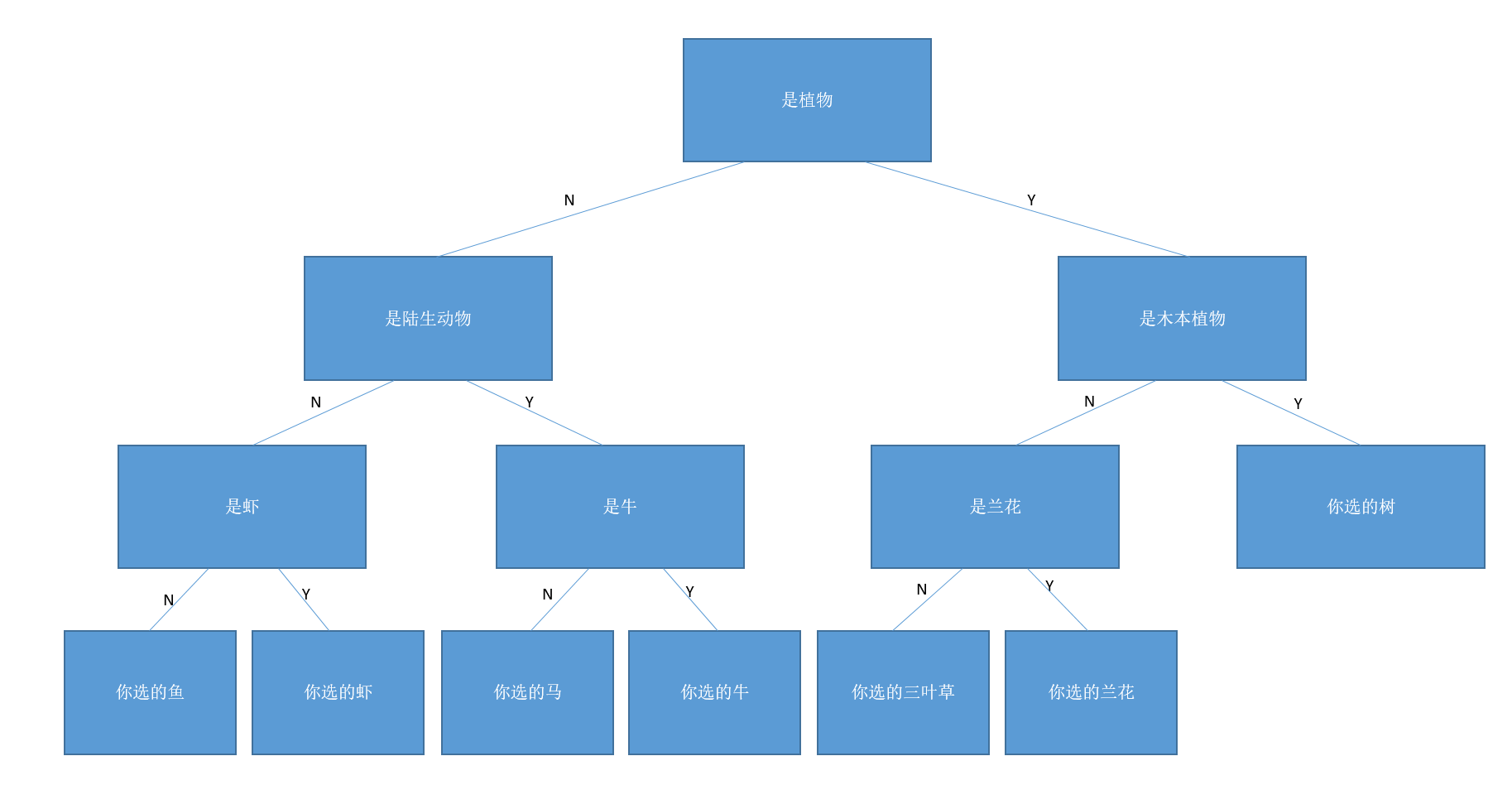
- 将树连接完成以后,
decision()方法将根据用户给出的答案读取相应子树或打印出结果。
public void decision() {
Scanner scan = new Scanner(System.in);
LinkedBinaryTree<String> current = tree;
System.out.println("请在树、鱼、虾、马、牛、三叶草、兰花中选择一种");
while (current.size() > 1) {
System.out.println(current.getRootElement());
if (scan.nextLine().equalsIgnoreCase("N")) current = current.getLeft();
else current = current.getRight();
}
System.out.println(current.getRootElement());
}
构建表达式树
OperateTree
- 思路:首先将中缀式转化为后缀式,这一部分可以使用之前在四则运算项目里面代码。然后就是将算式加到树中。
当遇到数字的时候入栈
当遇到操作符的时候前两个数字出栈,并以操作符为根节点把它们作为左右子树连接起来,然后压入栈
-
-
体现到代码中就是
switch (yangjingdian.charAt(i)) {
case '+':
BTNode node = new BTNode(yangjingdian.charAt(i));
node.right = stack.pop();
node.left = stack.pop();
stack.push(node);
break;
case '-':
BTNode node = new BTNode(yangjingdian.charAt(i));
node.right = stack.pop();
node.left = stack.pop();
stack.push(node);
break;
case '*':
BTNode node = new BTNode(yangjingdian.charAt(i));
node.right = stack.pop();
node.left = stack.pop();
stack.push(node);
break;
case '/':
BTNode node = new BTNode(yangjingdian.charAt(i));
node.right = stack.pop();
node.left = stack.pop();
stack.push(node);
break;
default:
stack.push(new BTNode(yangjingdian.charAt(i)));
break;
}
- 代码中的
case可以合在一起,简化后的代码就是
switch (yangjingdian.charAt(i)) {
case '+':
case '-':
case '*':
case '/':
BTNode node = new BTNode(yangjingdian.charAt(i));
node.right = stack.pop();
node.left = stack.pop();
stack.push(node);
break;
default:
stack.push(new BTNode(yangjingdian.charAt(i)));
break;
}
- 外层需要一个for循环来遍历整个字符串
for (int i = 0; i < yangjingdian.length();i++)
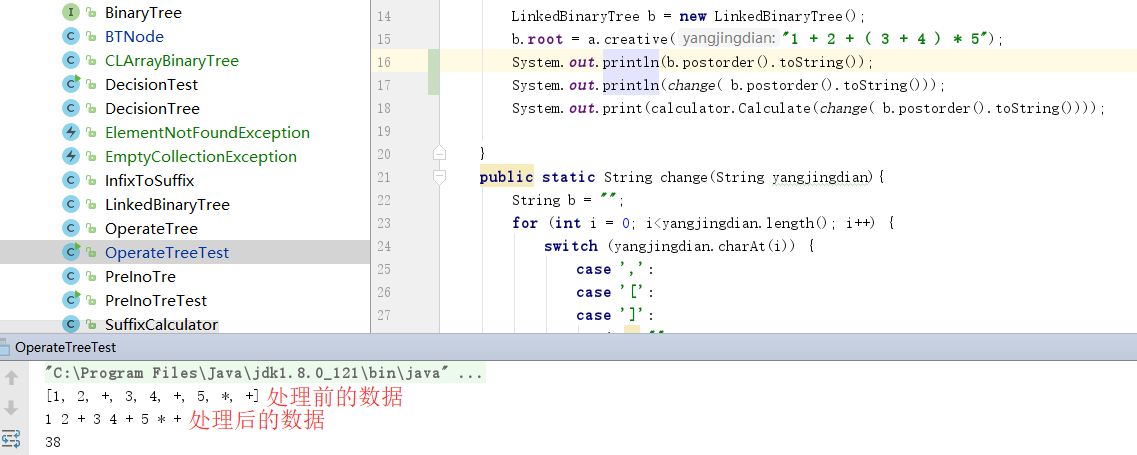
- 字符处理器:树引用了队列中的
toString方法,打印出来的数据是[1, +, 3]的样子,明显不符合算式输入的要求,所以就需要一个方法来过滤多余的东西
public static String change(String yangjingdian){
String b = "";
for (int i = 0; i<yangjingdian.length(); i++) {
switch (yangjingdian.charAt(i)) {
case ',':
case '[':
case ']':
b += "";
break;
default:
b += yangjingdian.charAt(i);
break;
}
}
return b;
}
二叉查找树
LinkedBinarySearchTree
- 由于查找树的
add()方法是特殊的,所以查找树中的数据是有序的,小值在左,大值在右(详见第八周学习总结)。所以直接获取最左面或最右面的节点就可以得到最小值或最大值。
public T findMin() {
BTNode s = root;
while (root.getLeft()!=null){
root = root.getLeft();
}
T data = root.getElement();
root = s;
return data;
}
public T findMax() {
BTNode s = root;
while (root.getRight()!=null){
root = root.getRight();
}
T data = root.getElement();
root = s;
return data;
}
红黑树分析
-
在之前的使用中就涉及过
HashMap,所以这次源码分析主要针对它 -
首先要了解红黑树到底是什么,它有最基本的五条性质
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个叶节点是黑色的。
性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
要知道为什么这些特性确保了这个结果,注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
在很多树数据结构的表示中,一个节点有可能只有一个子节点,而叶子节点不包含数据。用这种范例表示红黑树是可能的,但是这会改变一些属性并使算法复杂。为此,本文中我们使用 "nil 叶子" 或"空(null)叶子",如上图所示,它不包含数据而只充当树在此结束的指示。这些节点在绘图中经常被省略,导致了这些树好象同上述原则相矛盾,而实际上不是这样。与此有关的结论是所有节点都有两个子节点,尽管其中的一个或两个可能是空叶子。
-
参考:红黑树
-
方法摘要

-
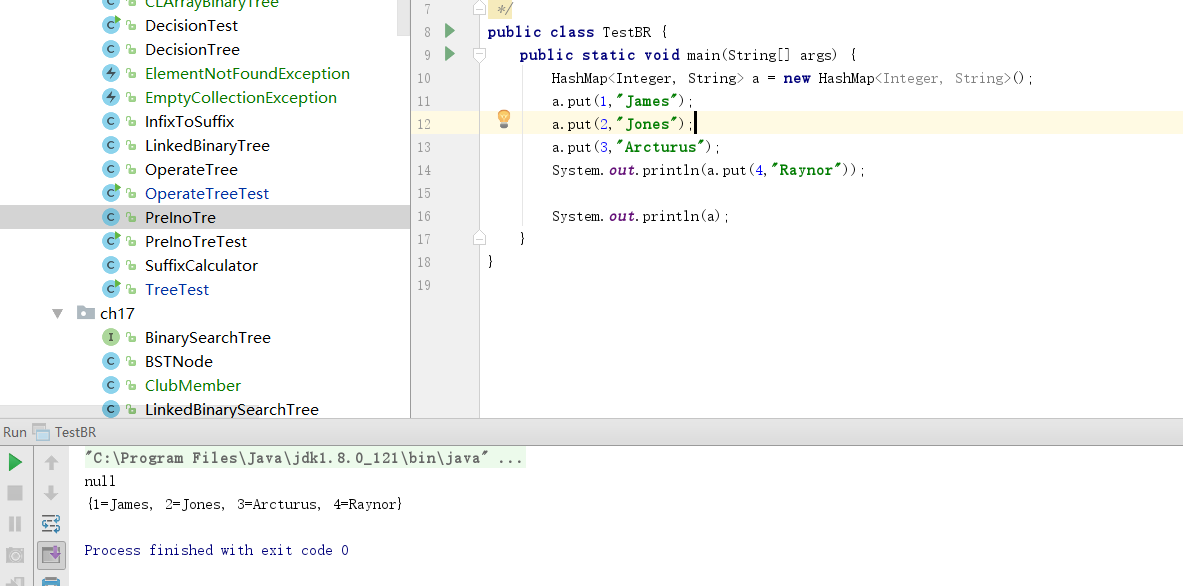
测试
put()方法和'toString()'方法
-
源代码
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}