数据结构与算法-java-平衡二叉树(AVL树)

平衡二叉树，是一种二叉排序树，其中每个结点的左子树和右子树的高度差至多等于1。它是一种高度平衡的二叉排序树。高度平衡？意思是说，要么它是一棵空树，要么它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

 

 为什么需要平衡二叉树，下图很好解析了为什么

 

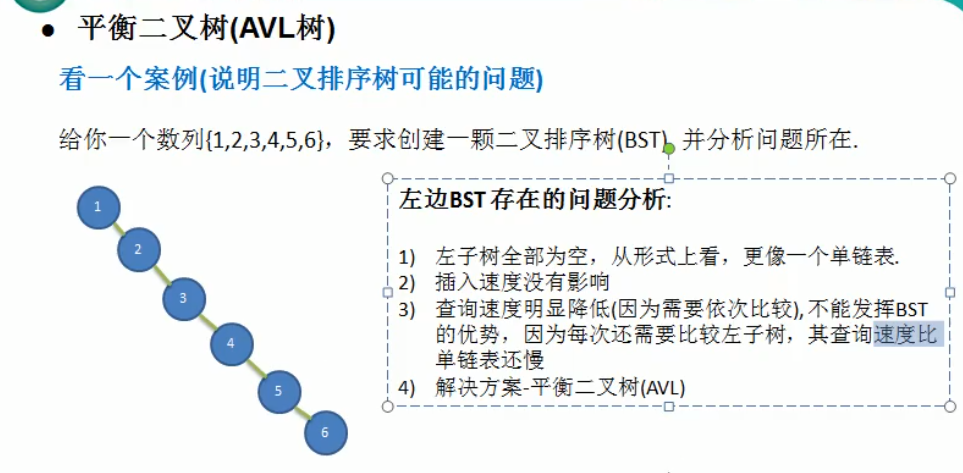
 图中我们可以看出二叉树如果这样，那么我们的查找将会非常浪费时间

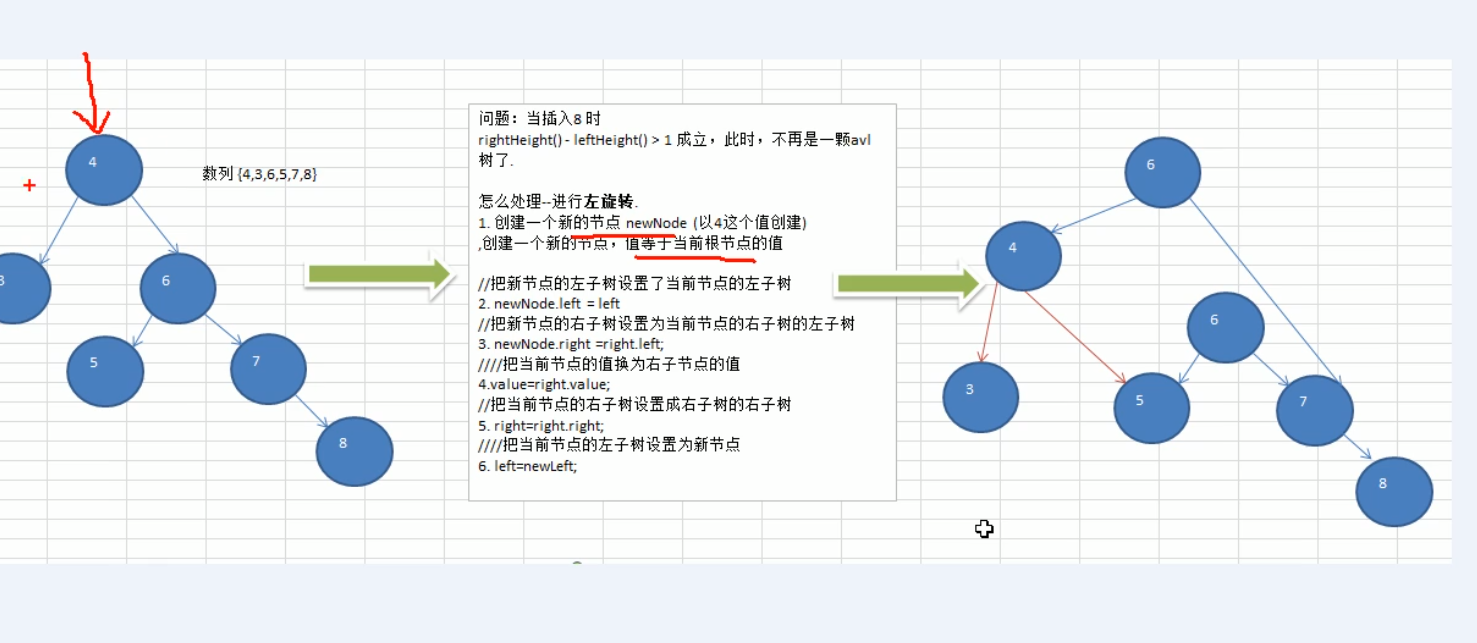
而怎样旋转成平衡树呢

简而言之就是左子树层数多就右旋转，右子树层数多左旋转

如：右节点层数是3左节点层数是1.差值大于1.需要左旋转

 

package AVLTree;

import sun.font.DelegatingShape;

public class AVLTreeDemo {
    public static void main(String[] args) {
        int []arr = {4,3,6,5,7,8};
         AVLTree avlTree = new AVLTree();
         for(int i=0;i<arr.length;i++)
         {
                avlTree.Treeadd(new Node(arr[i]));
         }
        System.out.println("中序遍历");
         avlTree.TreeinfixOrder();
        System.out.println("在平衡处理之后");
        System.out.println("树的高度Wie"+avlTree.getRoot().height());
        System.out.println("树的左子高度Wie"+avlTree.getRoot().leftHeight());
        System.out.println("树的右子高度Wie"+avlTree.getRoot().rightHeight());
    }

}

class AVLTree{
    private  Node root;

    public Node getRoot() {
        return root;
    }

    public void Treeadd(Node node){
        if(root==null)
        {
            root=node;
        }
        else {
            root.add(node);
        }

    }
    public void TreeinfixOrder(){
        if (root == null) {
            System.out.println("为空，无法遍历");
        }
        else {
            root.infixOrder();
        }
    }

    public Node Treesearch(int value)
    {
        if (root == null) {
            return null;
        }
        else {
            return root.search(value);
        }
    }
    public Node TreesearchParent(int value)
    {
        if (root == null) {
            return null;
        }
        else {
            return root.searchPartent(value);
        }
    }
    public void delNode(int value)
    {
        if(root == null)
        {
            return;
        }
        else {
            Node tar = Treesearch(value);
            //如果没有找到
            if(tar==null)
            {
                return ;
            }
            if(root.left==null&&root.right==null)
            {
                root=null;//root置为空
                return;
            }
            //找父节点
            Node parent = TreesearchParent(value);
            //如果要删除的节点是叶子节点
            if(tar.left==null&&tar.right==null)
            {
                //判断tar是父节点的左子节点还是右子节点
                if(parent.left!=null&&parent.left.value==value)
                {
                    parent.left=null;  //设置为空，相对于删除并根据jvm的垃圾回收机制，会自动回收。
                }
                else if(parent.right!=null&&parent.right.value==value){
                    parent.right=null; //设置为空，相对于删除并根据jvm的垃圾回收机制，会自动回收。
                }
            }
        }
    }

}

class Node{
    int value;
    Node left;
    Node right;
    public Node(int value) {
        this.value = value;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }

    //返回以该节点为根节点的树的高度
    public int height(){
        return Math.max(left==null?0:left.height(),right==null?0:right.height()+1);
    }
    //返回左子树的高度
    public int  leftHeight(){
        if(left==null)
        {
            return 0;
        }
        else {
        return left.height();
        }
    }
    //返回右子树的高度
    public int  rightHeight(){
        if(right==null)
        {
            return 0;
        }
        else {
            return right.height();
        }
    }
    //左旋转的方法
    private void leftRotate(){
        //创建新节点，以当前根结点的值
        Node newNode  = new Node(value);
        //把新的节点的左子树设置成当前节点的左子树
        newNode.left = left;
        //把新的节点的右子树设置成带你过去节点的右子树的左子树
        newNode.right = right.left;
        //当前节点的值替换为右子节点的值
        value=right.value;
        //吧当前节点的右子树设置为当前节点的右子树的右子树
        right=right.right;
        //吧当前节点的左子树或者说左子节点设置成新的节点
        left= newNode;

    }

    public void add(Node node)
    {
        if(node==null)
        {
            return;
        }
        //判断传入的结点的值，和当前子树的根结点的值关系,<即插入左
        if(node.value<this.value)
        {
            if(this.left==null)
            {
                this.left=node;
            }
            else {
                this.left.add(node);
            }

        }  //>即右插
        else {
            if(this.right==null)
            {
                this.right=node;
            }
            else {
                this.right.add(node);
            }
        }

        //当添加完节点后发现满足右子树-左子树>1所以，左旋转
        if(rightHeight()-leftHeight()>1)
        {
            leftRotate();
        }
    }

    //中序遍历
    public void infixOrder(){
        if (this.left != null)
        {
            this.left.infixOrder();
        }
        System.out.println(this);
        if(this.right!=null)
        {
            this.right.infixOrder();
        }
    }

    //如果找到返回该节点，没有就返回null
    public Node search(int value){
        if(value==this.value)   //说明就是该节点
        {
            return  this;
        }
        else if(value<this.value){  //小. 左找
            if(this.left==null)
            {
                return null;
            }
            return this.left.search(value); //--的过程
        }
        else {
            if (this.right == null) {

                return null;
            }
            return this.right.search(value);//--的过程
        }

    }
    //查找要删除节点的父节点
    public Node searchPartent(int value)
    {
        //该节点就是要删除的节点的父节点
        if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)){
            return this;
        }
        else {
            if(value<this.value&&this.left!=null)
            {
                return this.left.searchPartent(value);//向左子树递归查找
            }
            else if(value>=this.value&&this.right!=null)
            {
                return this.right.searchPartent(value);//向右子树递归查找
            }
            else {
                return null;
            }

        }
    }

}

 

 左旋转就实现了，那么右旋转也类似即可。