数据结构与算法-java-二叉树

首先我们了解一下树：

树状图是一种数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

每个结点有零个或多个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树

那我们再树之前来看看数组的底层

 

 

 

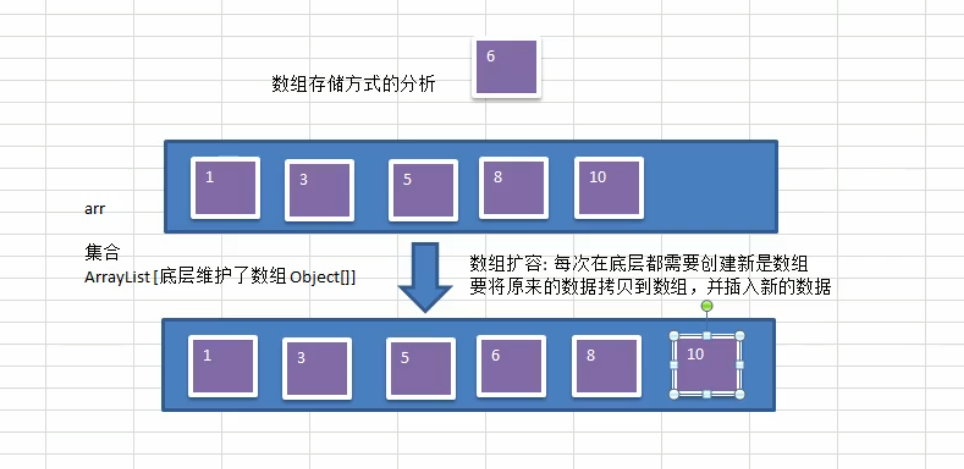
 数组如果不够需要扩容，比较麻烦需要创建新的数组，拷贝，插入新数据等，

集合的话也是，因为集合ArrayList底层也是一个Object[]数组，一样的需要扩容麻烦。

那么链式存储呢？，并且还插入删除都方便快速。但是！链式储蓄检索效率太低，想一想一百万个数在链表

而我们要查找80万。是不是害的从头结点开始一个一个遍历！

所以出现树插入删除方便检索也方便！以二叉树为第一个例子

 

 

 

 那么这里面比较难理解就是权，那什么是权呢 ：二叉树中的权值就是对叶子结点赋予的一个有意义的数量值。就是本身数值。

二叉树的遍历：

思路：如下

 

 

 看代码的顺序是先class HeroNode创建节点结构 再class BinaryTree创建树结构最后main

package tree;

//c创建节点
class HeroNode {
    public int no;
    public String name;
    public HeroNode left;
    public HeroNode right;

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public HeroNode getLeft() {
        return left;
    }

    public void setLeft(HeroNode left) {
        this.left = left;
    }

    public HeroNode getRight() {
        return right;
    }

    public void setRight(HeroNode right) {
        this.right = right;
    }

    public HeroNode(int no, String name) {
        this.no = no;
        this.name = name;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "no=" + no +
                ", name='" + name + '\'' +
                '}';
    }
    //前序
    public void preOrder(){
        System.out.println(this);//先输出父子节点
        if(this.left!=null){
            //递归向左子树前序遍历
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
    //中序
    public void infixOrder(){
        if(this.left!=null){
            //递归向左子树中序遍历
            this.left.infixOrder();
        }
        System.out.println(this);//先输出父子节点
        //递归向右子树中序遍历
        if(this.right!=null){
            this.right.infixOrder();
        }
    }
    //后序
    public void postOrder(){
        if(this.right!=null){
            //递归向左子树后序遍历
            this.right.postOrder();
        }
        System.out.println(this);//先输出父子节点
        //递归向左子树后序遍历
        if(this.left!=null){
            this.left.postOrder();
        }
    }
}

//创建二叉树
class BinaryTree{
    private HeroNode root;
    public void setRoot(HeroNode root)
    {
        this.root=root;
    }
    //前序遍历实现
    public void TreeProOrder(){
        if(this.root!=null)
        {
            this.root.preOrder();
        }
        else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    //中序遍历实现
    public void TreeInfixOrder(){
        if(this.root!=null)
        {
            this.root.infixOrder();
        }
        else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    //后序遍历实现
    public void TreePostOrder(){
        if(this.root!=null)
        {
            this.root.postOrder();
        }
        else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
}

public class BinaryTreeDemo {
    public static void main(String[] args) {
        //创建一刻二叉树
        BinaryTree binaryTree = new BinaryTree();
        //创建需要的节点
        HeroNode root = new HeroNode(1,"宋江");
        HeroNode heroNode2 = new HeroNode(2,"吴用");
        HeroNode heroNode3 = new HeroNode(3,"卢俊义");
        HeroNode heroNode4 = new HeroNode(4,"林冲");
        //手动创建二叉树
        root.setLeft(heroNode2);
        root.setRight(heroNode3);
        heroNode3.setRight(heroNode4);
        binaryTree.setRoot(root);
        //测试
        System.out.println("前序遍历");
        binaryTree.TreeProOrder();
        System.out.println("中序遍历");
        binaryTree.TreeInfixOrder();
        System.out.println("后序遍历");
        binaryTree.TreePostOrder();
    }
}

 

 

 那么了解了二叉树的建立，遍历之后，来看看二叉树的查找

 那么还是思路分析一下

 在前面代码的搭建树的基础上写查询方法

package tree;

import java.util.HashMap;

//c创建节点
class HeroNode {
    public int no;
    public String name;
    public HeroNode left;
    public HeroNode right;

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public HeroNode getLeft() {
        return left;
    }

    public void setLeft(HeroNode left) {
        this.left = left;
    }

    public HeroNode getRight() {
        return right;
    }

    public void setRight(HeroNode right) {
        this.right = right;
    }

    public HeroNode(int no, String name) {
        this.no = no;
        this.name = name;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "no=" + no +
                ", name='" + name + '\'' +
                '}';
    }

    //前序
    public void preOrder() {
        System.out.println(this);//先输出父子节点
        if (this.left != null) {
            //递归向左子树前序遍历
            this.left.preOrder();
        }
        if (this.right != null) {
            this.right.preOrder();
        }
    }

    //中序
    public void infixOrder() {
        if (this.left != null) {
            //递归向左子树中序遍历
            this.left.infixOrder();
        }
        System.out.println(this);//先输出父子节点
        //递归向右子树中序遍历
        if (this.right != null) {
            this.right.infixOrder();
        }
    }

    //后序
    public void postOrder() {
        if (this.right != null) {
            //递归向左子树后序遍历
            this.right.postOrder();
        }
        System.out.println(this);//先输出父子节点
        //递归向左子树后序遍历
        if (this.left != null) {
            this.left.postOrder();
        }
    }

    //前序遍历查找
    public HeroNode preOrderSearch(int no) {
        //比较当前节点是不是，就是则返回
        if (this.no == no) {
            return this;
        }
        //定义一个返回值
        HeroNode resultNode = null;
        //判断左子节点是否为空，不为空就递归前序查找
        //递归前序查找，找到节点，则返回
        if (this.left != null) {
            resultNode = this.left.preOrderSearch(no); //这里其实有点像以前写的链表的temp=temp.next即下一位
        }
        //在左子树找到了这里就返回了resultNode没有后面的事了
        if (resultNode != null) {
            return resultNode;
        }

        if(this.right!=null)
        {
            resultNode = this.right.preOrderSearch(no);
        }
        //如果都没找到就为空，在右子节点找到了就在这里返回
        return  resultNode;
    }
    //中序遍历查找
    public HeroNode infixOrderSearch(int no) {
        HeroNode resNode = null;
        //判断当前节点的左子节点是否为空
        if (this.left != null) {
            resNode = this.left.infixOrderSearch(no);
        }
        if (resNode != null) {
            //找到就直接返回了
            return resNode;
        }
        if(this.no ==no)
        {
            return this;
        }
        if(this.right!=null)
        {
            resNode =this.right.infixOrderSearch(no);
        }
        return resNode;

    }

 }





//创建二叉树
class BinaryTree{
    private HeroNode root;
    public void setRoot(HeroNode root)
    {
        this.root=root;
    }
    //前序遍历实现
    public void TreeProOrder(){
        if(this.root!=null)
        {
            this.root.preOrder();
        }
        else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    //中序遍历实现
    public void TreeInfixOrder(){
        if(this.root!=null)
        {
            this.root.infixOrder();
        }
        else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    //后序遍历实现
    public void TreePostOrder(){
        if(this.root!=null)
        {
            this.root.postOrder();
        }
        else {
            System.out.println("二叉树为空，无法遍历");
        }
    }

    //前序遍历查找
    public HeroNode TreePreOrderSearch(int no){
        if(root!=null){
            return root.preOrderSearch(no);
        }
        else {
            return null;
        }
    }
    //中序遍历查找
    public HeroNode TreeInfixOrderSearch(int no){
        if(root!=null){
            return root.infixOrderSearch(no);
        }
        else {
            return null;
        }
    }
}

public class BinaryTreeDemo {
    public static void main(String[] args) {
        //创建一刻二叉树
        BinaryTree binaryTree = new BinaryTree();
        //创建需要的节点
        HeroNode root = new HeroNode(1,"宋江");
        HeroNode heroNode2 = new HeroNode(2,"吴用");
        HeroNode heroNode3 = new HeroNode(3,"卢俊义");
        HeroNode heroNode4 = new HeroNode(4,"林冲");
        //手动创建二叉树
        root.setLeft(heroNode2);
        root.setRight(heroNode3);
        heroNode3.setRight(heroNode4);
        binaryTree.setRoot(root);
        //测试
        System.out.println("前序遍历");
        binaryTree.TreeProOrder();
        System.out.println("中序遍历");
        binaryTree.TreeInfixOrder();
        System.out.println("后序遍历");
        binaryTree.TreePostOrder();

        //前序遍历
        System.out.println("前序遍历方式查询");
        HeroNode res=binaryTree.TreePreOrderSearch(4);
        if(res!=null)
        {
            System.out.println("找到了"+res);
        }
        else {
            System.out.println("没找到");
        }
    }
}