PyTorch的Autograd机制

1.requires_grad

当我们创建一个张量 (tensor) 的时候，如果没有特殊指定的话，那么这个张量是默认是不需要求导的。我们可以通过 tensor.requires_grad 来检

查一个张量是否需要求导。在张量间的计算过程中，如果在所有输入中，有一个输入需要求导，那么输出一定会需要求导；相反，只有当所有输入都

不需要求导的时候，输出才会不需要。

举一个比较简单的例子，比如我们在训练一个网络的时候，我们从 DataLoader 中读取出来的一个 mini-batch的数据，这些输入默认是不需要求导的，

其次，网络的输出我们没有特意指明需要求导吧，Ground Truth 我们也没有特意设置需要求导吧。这么一想，哇，那我之前的那些 loss 咋还能自动求

导呢？其实原因就是上边那条规则，虽然输入的训练数据是默认不求导的，但是，我们的 model 中的所有参数，它默认是求导的，这么一来，其中只要

有一个需要求导，那么输出的网络结果必定也会需要求的。来看个实例：

input = torch.randn(8, 3, 50, 100)
print(input.requires_grad)
# False

net = nn.Sequential(nn.Conv2d(3, 16, 3, 1),
                    nn.Conv2d(16, 32, 3, 1))
for param in net.named_parameters():
    print(param[0], param[1].requires_grad)
# 0.weight True
# 0.bias True
# 1.weight True
# 1.bias True

output = net(input)
print(output.requires_grad)
# True

我们试试把网络参数的 requires_grad 设置为 False 会怎么样，同样的网络：

input = torch.randn(8, 3, 50, 100)
print(input.requires_grad)
# False

net = nn.Sequential(nn.Conv2d(3, 16, 3, 1),
                    nn.Conv2d(16, 32, 3, 1))
for param in net.named_parameters():
    param[1].requires_grad = False
    print(param[0], param[1].requires_grad)
# 0.weight False
# 0.bias False
# 1.weight False
# 1.bias False

output = net(input)
print(output.requires_grad)
# False

我们可以通过这种方法，在训练的过程中冻结部分网络，让这些层的参数不再更新。

 

2. torch.no_grad()

当我们在做 evaluating 的时候（不需要计算导数），我们可以将推断（inference）的代码包裹在 with torch.no_grad(): 之中，

以达到暂时不追踪网络参数中的导数的目的，总之是为了减少可能存在的计算和内存消耗。

x = torch.randn(3, requires_grad = True)
print(x.requires_grad)
# True
print((x ** 2).requires_grad)
# True

with torch.no_grad():
    print((x ** 2).requires_grad)
    # False

print((x ** 2).requires_grad)
# True

 

3. 计算图

了解自动求导背后的原理和规则，对我们写出一个更干净整洁甚至更高效的 PyTorch 代码是十分重要的。但是，现在已经有了很多封装好的 API，

我们在写一个自己的网络的时候，可能几乎都不用去注意求导这些问题，因为这些 API 已经在私底下处理好了这些事情。现在我们往往只需要搭建

个想要的模型，处理好数据的载入，调用现成的 optimizer 和 loss function，直接开始训练就好了。仔细一想，连需要设置 requires_grad = True

的地方好像都没有。有人可能会问，那我们去了解自动求导还有什么用啊？

原因有很多，可以帮我们更深入地了解 PyTorch 这些宽泛的理由我就不说了，我举一个例子：当我们想使用一个 PyTorch 默认中并没有的 loss function

的时候，比如目标检测模型 YOLO 的 loss，我们可能就得自己去实现。如果我们不熟悉基本的 PyTorch 求导机制的话，对于实现过程中比如 tensor 的

in-place 操作等等很容易出错，导致需要话很长时间去 debug，有的时候即使定位到了错误的位置，也不知道如何去修改。相反，如果我们理清楚了背后

的原理，我们就能很快地修改这些错误，甚至根本不会去犯这些错误。鉴于现在官方支持的 loss function 并不多，而且深度学习领域日新月异，很多新

的效果很好的 loss function 层出不穷，如果要用的话可能需要我们自己来实现。基于这个原因，我们了解一下自动求导机制还是很有必要的。

计算图通常包含两种元素，一个是 tensor，另一个是 Function。张量 tensor 不必多说，但是大家可能对 Function 比较陌生。这里 Function 指的是

在计算图中某个节点（node）所进行的运算，比如加减乘除卷积等等之类的，Function 内部有 forward() 和 backward() 两个方法，分别应用于正向、反向传播。

举个例子：

input = torch.ones([2, 2], requires_grad=False)
w1 = torch.tensor(2.0, requires_grad=True)
w2 = torch.tensor(3.0, requires_grad=True)
w3 = torch.tensor(4.0, requires_grad=True)

l1 = input * w1
l2 = l1 + w2
l3 = l1 * w3
l4 = l2 * l3
loss = l4.mean()


print(w1.data, w1.grad, w1.grad_fn)
# tensor(2.) None None

print(l1.data, l1.grad, l1.grad_fn)
# tensor([[2., 2.],
#         [2., 2.]]) None <MulBackward0 object at 0x000001EBE79E6AC8>

print(loss.data, loss.grad, loss.grad_fn)
# tensor(40.) None <MeanBackward0 object at 0x000001EBE79D8208>

我们可以简单地画一下它的计算图：

　　

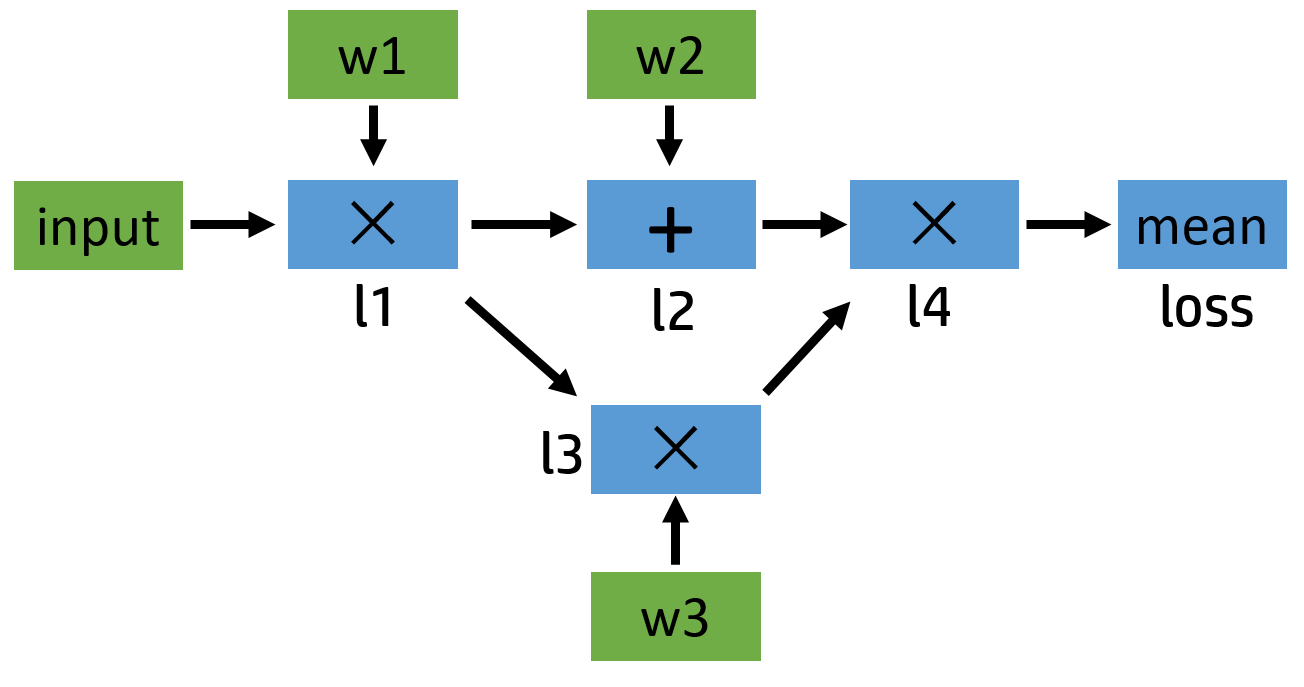
对于任意一个张量来说，我们可以用 tensor.is_leaf 来判断它是否是叶子张量（leaf tensor）。在反向传播过程中，只有 is_leaf=True 的时候，

需要求导的张量的导数结果才会被最后保留下来。在图中的叶子节点我用绿色标出了。可以看出来，被叫做叶子，可能是因为漂浮在主干之外，没有

子节点，因为它们都是被用户创建的，不是通过其他节点生成。

我们有办法保留中间变量的导数吗？当然有，通过使用 retain_grad() 就可以：

# 和前边一样
# ...
loss = l4.mean()

l1.retain_grad()
l4.retain_grad()
loss.retain_grad()

loss.backward()

print(loss.grad)
# tensor(1.)
print(l4.grad)
# tensor([[0.2500, 0.2500],
#         [0.2500, 0.2500]])
print(l1.grad)
# tensor([[7., 7.],
#         [7., 7.]])

 

4. inplace 操作

inplace 指的是在不更改变量的内存地址的情况下，直接修改变量的值。我们还是来看个例子：

a = torch.tensor([1.0, 3.0], requires_grad=True)
b = a + 2
print(b._version) # 0

loss = (b * b).mean()
b[0] = 1000.0
print(b._version) # 1

loss.backward()
# RuntimeError: ...

PyTorch 是怎么检测 tensor 发生了 inplace 操作呢？答案是通过 tensor._version 来检测的。每次 tensor 在进行 inplace 操作事，变量 _version 就

会加1，其初始值为0。在正向传播过程中，求导系统记录的 b 的 version 是0，但是在进行反向传播的过程中，求导系统发现 b 的 version 变成1了，所以

就会报错了。但是还有一种特殊情况不会报错，就是反向传播求导的时候如果没用到 b 的值（比如 y = x + 1， y 关于 x 的导数是1，和 x 无关），自然就

不会去对比 b 前后的 version 了，所以不会报错。

上边我们所说的情况是针对非叶子节点的，对于 requires_grad=True 的叶子节点来说，要求更加严格了，甚至在叶子节点被使用之前修改它的值都不行。

a = torch.tensor([10., 5., 2., 3.], requires_grad=True)
print(a, a.is_leaf)
# tensor([10.,  5.,  2.,  3.], requires_grad=True) True

a[:] = 0
print(a, a.is_leaf)
# tensor([0., 0., 0., 0.], grad_fn=<CopySlices>) False

loss = (a*a).mean()
loss.backward()

在进行对 a 的重新 inplace 赋值之后，表示了 a 是通过 copy operation 生成的，grad_fn 都有了，所以自然而然不是叶子节点了。

非叶子节点的导数在默认情况下是不会被保存的，本来是该有导数值保留的变量，现在成了导数会被自动释放的中间变量了，所以 PyTorch 就给你报错了。

a = torch.tensor([10., 5., 2., 3.], requires_grad=True)
a.add_(10.) # 或者 a += 10.
# RuntimeError: a leaf Variable that requires grad has been used in an in-place operation.

这个更厉害了，不等到你调用 backward，只要你对需要求导的叶子张量使用了这些操作，马上就会报错。那是不是需要求导的叶子节点一旦被初始化赋值

之后，就不能修改它们的值了呢？我们如果在某种情况下需要重新对叶子变量赋值该怎么办呢？有办法！　

# 方法一
a = torch.tensor([10., 5., 2., 3.], requires_grad=True)
print(a, a.is_leaf, id(a))
# tensor([10.,  5.,  2.,  3.], requires_grad=True) True 2501274822696

a.data.fill_(10.)
# 或者 a.detach().fill_(10.)
print(a, a.is_leaf, id(a))
# tensor([10., 10., 10., 10.], requires_grad=True) True 2501274822696

loss = (a*a).mean()
loss.backward()
print(a.grad)
# tensor([5., 5., 5., 5.])

# 方法二
a = torch.tensor([10., 5., 2., 3.], requires_grad=True)
print(a, a.is_leaf)
# tensor([10.,  5.,  2.,  3.], requires_grad=True) True

with torch.no_grad():
    a[:] = 10.
print(a, a.is_leaf)
# tensor([10., 10., 10., 10.], requires_grad=True) True

loss = (a*a).mean()
loss.backward()
print(a.grad)
# tensor([5., 5., 5., 5.])

修改的方法有很多种，核心就是修改那个和变量共享内存，但 requires_grad=False 的版本的值，比如通过 tensor.data 或者 tensor.detach()。我们需要注

意的是，要在变量被使用之前修改，不然等计算完之后再修改，还会造成求导上的问题。

在 0.4.0 版本以前，.data 是用来取 Variable 中的 tensor 的，但是之后 Variable 被取消，.data 却留了下来。现在我们调用 tensor.data，可以得到

tensor的数据 + requires_grad=False 的版本，而且二者共享储存空间，也就是如果修改其中一个，另一个也会变。因为 PyTorch 的自动求导系统不会追踪

tensor.data 的变化，所以使用它的话可能会导致求导结果出错。官方建议使用 tensor.detach() 来替代它，二者作用相似，但是 detach 会被自动求导系统

追踪，使用起来很安全。

为什么 PyTorch 的求导不支持绝大部分 inplace 操作呢？从上边我们也看出来了，因为真的很 tricky。比如有的时候在一个变量已经参与了正向传播的计算，

之后它的值被修改了，在做反向传播的时候如果还需要这个变量的值的话，我们肯定不能用那个后来修改的值吧，但没修改之前的原始值已经在内存被释放掉了，

我们怎么办？一种可行的办法就是我们在 Function 做 forward 的时候每次都开辟一片空间储存当时输入变量的值，这样无论之后它们怎么修改，都不会影响了，

反正我们有备份在存着。但这样有什么问题？这样会导致内存（或显存）使用量大大增加。因为我们不确定哪个变量可能之后会做 inplace 操作，所以我们每个

变量在做完 forward 之后都要被储存一个备份，成本太高了。除此之外，inplace operation 还可能造成很多其他求导上的问题。

 

5. CPU and GPU

我们想把 GPU tensor 转换成 numpy 变量的时候，需要先将 tensor 转换到 CPU 中去，因为 Numpy 是 CPU-only 的。其次，如果 tensor 需要求导的话，还

需要加一步 detach，再转成 Numpy 。例子如下：

x  = torch.rand([3,3], device='cuda')
x_ = x.cpu().numpy()

y  = torch.rand([3,3], requires_grad=True, device='cuda').
y_ = y.cpu().detach().numpy()
# y_ = y.detach().cpu().numpy() 也可以
# 二者好像差别不大？我们来比比时间：
start_t = time.time()
for i in range(10000):
    y_ = y.cpu().detach().numpy()
print(time.time() - start_t)
# 1.1049120426177979

start_t = time.time()
for i in range(10000):
    y_ = y.detach().cpu().numpy()
print(time.time() - start_t)
# 1.115112543106079
# 时间差别不是很大，当然，这个速度差别可能和电脑配置
# （比如 GPU 很贵，CPU 却很烂）有关。