Skyline查询
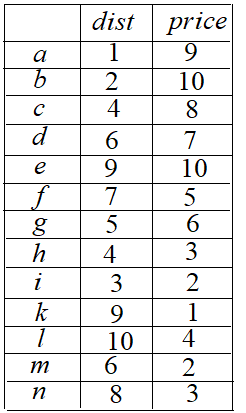
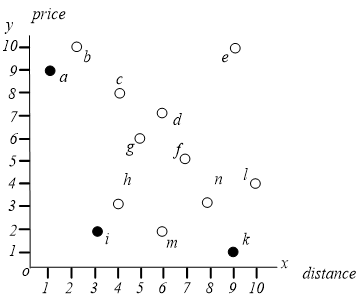
假设一个数据库存储每个酒店的以下信息：它的价格（夜间价格）、离海滩的距离。用户希望检索“最佳”酒店，如何比较两个酒店的质量呢？
$a$ 比 $b$ 好吗？是的，$a$ 酒店比 $b$ 酒店更便宜，而且离海滩更近，我们说 $a$ 支配 $b$。
$a$ 是不是比 $i$ 好呢？它们是不可比的。一些用户可能更喜欢 $a$（因为它离海滩更近），而另一些用户可能更喜欢 $i$（因为它更便宜）。
skyline 包含了所有不受其它酒店支配的酒店。skyline = $\left \{ a,i,k \right \}$，而非 skyline 酒店在大多数情况下不会被用户考虑。
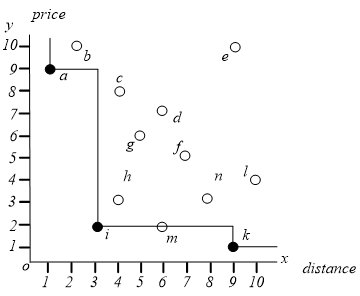
skyline 查询算法用到了两个重要的性质：
1）支配传递性：如果 $p_1$ 支配 $p_2$，$p_2$ 支配 $p_3$，那么我们就有 $p_1$ 支配 $p_3$。
2）如果一个点不能支配另一个点，那么反之亦然。
1. Block Nested Loop (BNL)
这个是最基本的查询算法，通过暴力搜索，判断每个酒店是否有被其他酒店支配，平方时间复杂度。
2. Sort First Skyline (SFS)
SFS是一种改进的BNL。首先根据（单调）偏好函数对整个数据集按某个维度进行排序。然后按 BNL 算法计算。
3. SCAN 扫描算法
顺序扫描表格，扫描过程中维护可能成为 skyline 点的列表，假设内存允许在 List 中最多保留 $3$ 个条目。
首先初始化 List，即将 $a$ 加入 List —— List = $\left \{ a \right \}$，接下来顺序扫描表格中的其它点，做如下两个判断：
a. 当前扫描到的点是否被 List 内的点所支配，如果没有被支配则执行步骤 $b$；否则将该点舍弃，然后扫描下一个点。
b. 当前扫描到的点是否支配 List 内的点，如果是则删除 List 内所有被当前点支配的点，然后执行步骤 $c$。
c. 判断 List 内的元素是否达到元素上限，如果没有，则将该点加入 List，否则将该点写入磁盘，并对当前 List 内的点做标记，只有第一次
溢出时做标记，表示当前了 List 内的点和磁盘上的点互不支配。
以上面酒店为例，它的 SACN 扫描算法过程如下：
1）因为 $a$ 支配 $b$，所以丢弃 $b$，被舍弃的点不会成为 skyline 点，如果 $b$ 会支配其它的点，那么这个点必然也被 $a$ 支配。
2）因为 $c$ 不被 List 里面的点支配，也不支配 List 里的点，所以 $c$ 加入 List —— List = $\left \{ a,c \right \}$。
4）因为 $d$ 不被 List 里面的点支配，也不支配 List 里的点，所以 $d$ 加入 List —— List = $\left \{ a,c,d \right \}$。
5）因为 $a$ 支配 $e$，所以丢弃 $e$。
6）$f$ 应该加入 List，但 List 已经满了，所以将 $f$ 写入磁盘文件，并标记所有当时在 List中的点 —— List = $\left \{ a^{'},c^{'},d^{'}\right \}$, File = $\left \{ f \right \}$。
7）因为 $g$ 支配 List 里面的 $d$，所以用 $g$ 替换 $d$ —— List = $\left \{ a^{'},c^{'},g \right \}$, File = $\left \{ f \right \}$，$g$ 是没有标记的。
8）因为 $h$ 支配 List 中的 $c,g$，所以用 $h$ 替换 $c,g$ —— List = $\left \{ a^{'},h \right \}$, File = $\left \{ f \right \}$
....
9）因为 $i$ 支配 $h$，所以用 $i$ 替换 $h$ —— List = $\left \{ a^{'},i \right \}$, File = $\left \{ f \right \}$
10）List = $\left \{ a^{'},i,k \right \}$, File = $\left \{ f \right \}$
11）$l,m,n$ 均被舍弃。
12）List 中有标记的点就是 skyline 点，然后还要针对 file 再做一遍 SCAN。
13）结果 $S = \left \{ a,i,k \right \}$。
4. Divide and Conquer (D&C)
把点分成几组，使得每组的数据都能够放进内存。分别处理这些组，然后合并它们的结果。$s_3$ 内的点直接成为 skyline，$s_4$ 内的点
直接舍去，因为它们显然会被 $s_3$ 内的点支配，然后用 $s_3$ 内的点来消除 $s_1$ 和 $s_4$ 中的非 skyline 点。
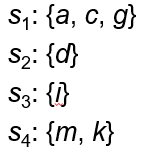
5. Nearest Neighbor (NN)
通过 $R$ 树的 $NN$ 算法来找 Skyline 点。
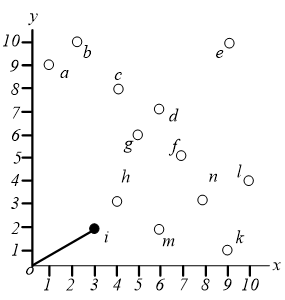
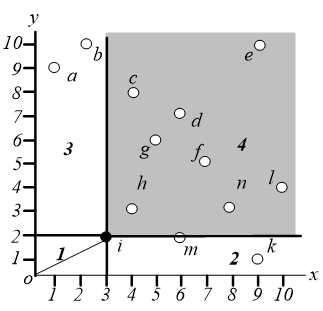
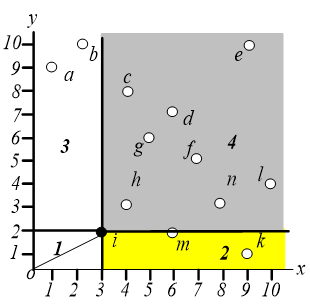
首先找到数据空间中距离原点最近的一个点，一般来说，任何距离指标都可以。这样我们就可以找到点 $i$，这个点必然是一个 skyline 点。
对于点 $i$，我们不需要考虑阴影区域中的那些点。区域 $1$ 也不需要考虑。事实上，在这个地区是没有意义的。区域 $2$ 和区域 $3$ 必须进一步探索。
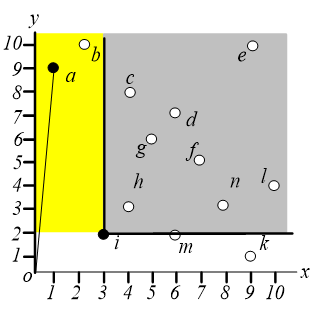
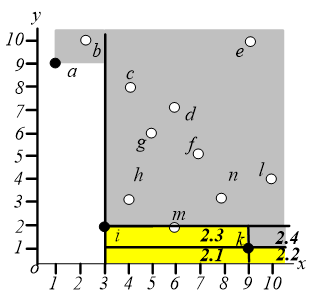
在区域 $3$ 中执行相同的操作，即找距离原点最近的点，这样就可以找到点 $a$，如下图，同样地，我们只需要关心区域 $3.2$ 和 $3.3$。
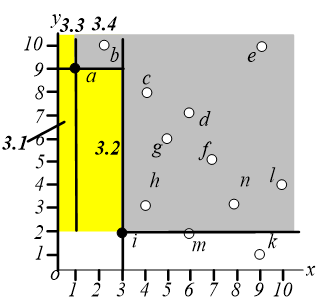
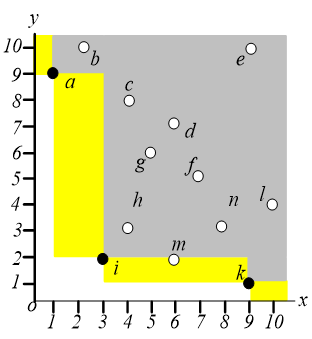
在区域 $2$ 中搜索离原点最近的点，可以找到 $k$ 点。
这个算法会经过 $3$ 次有效的 $NN$ 查询和 $4$ 次空查询。一般来说，如果 skyline 有 $s$ 个点，那么 $NN$ 执行 $s$ 次有用的 $NN$ 查询和 $s+1$ 次空查询。
6. Branch and Bound Skyline (BBS)
基于best-first NN算法实现。首先建立 $R$ 树。
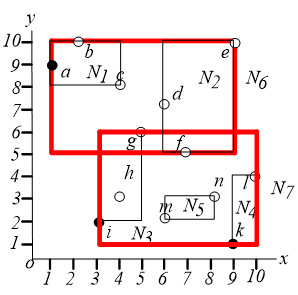
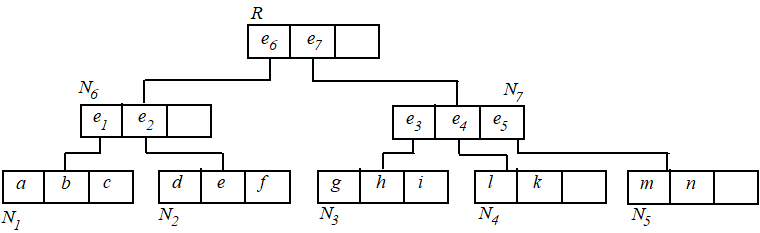
从根节点开始，算法过程如下：
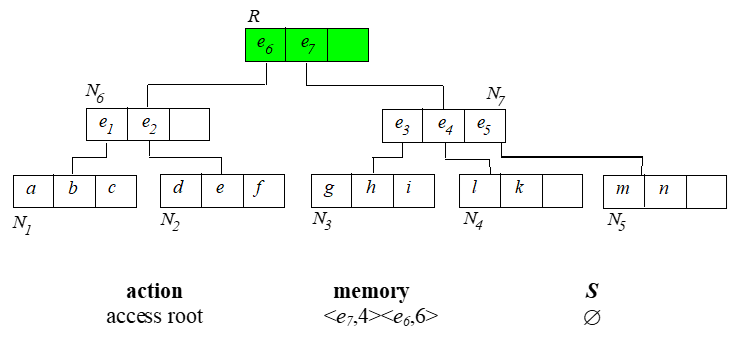
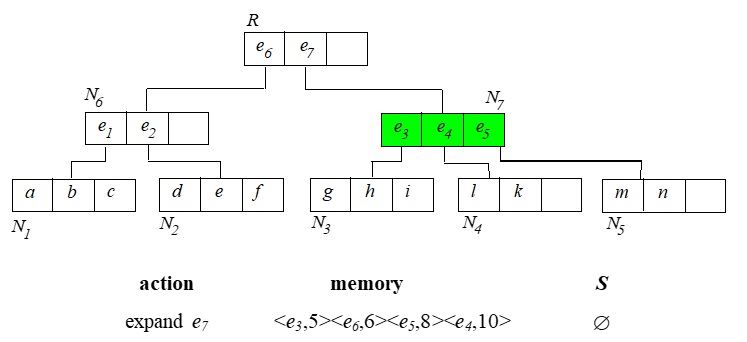
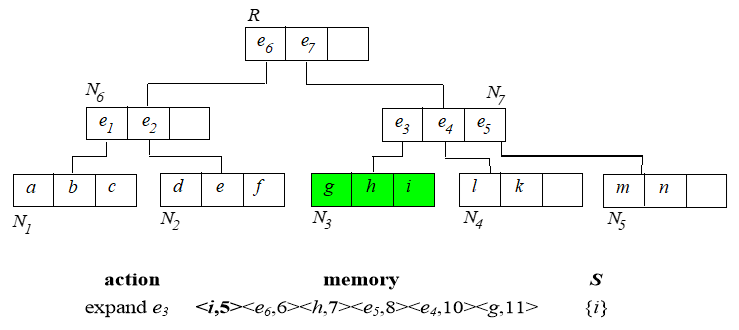
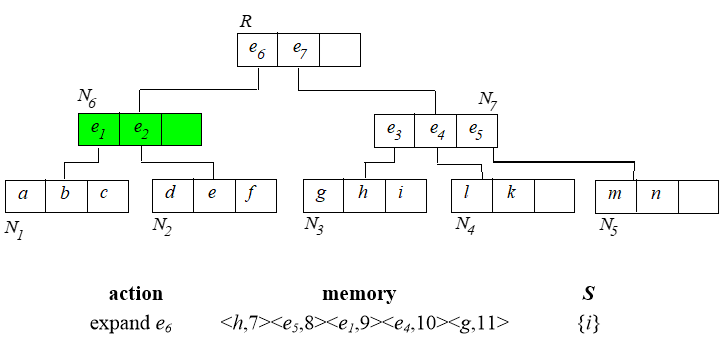
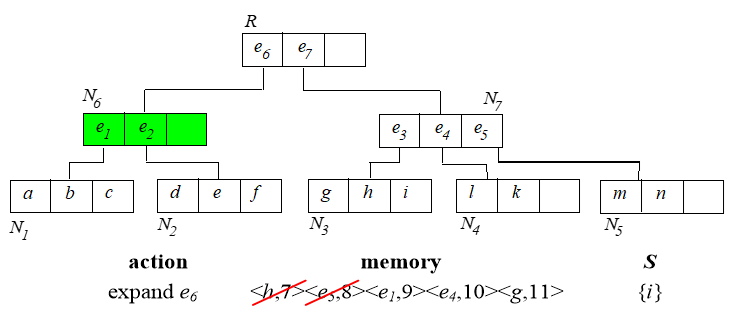
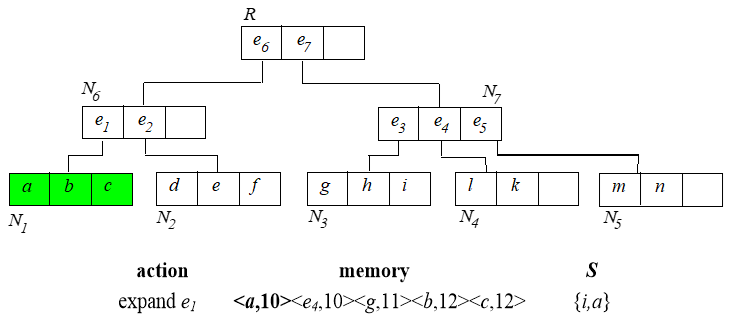
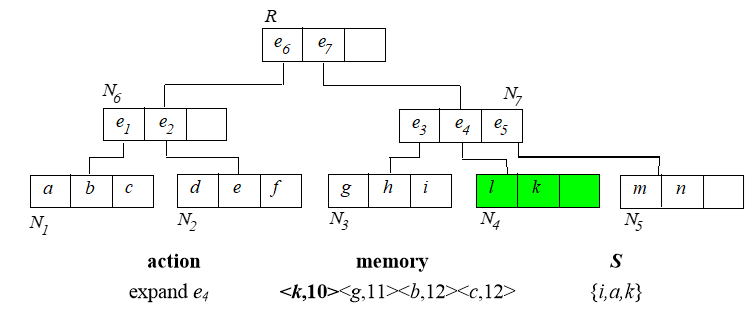
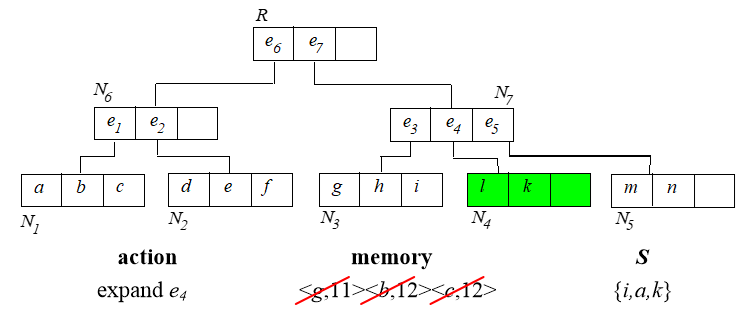
已经找到的 skyline 需要用来淘汰内存中排序的那些点。
