图像其实就是二元函数 f(x,y),只不过是离散的,图像梯度就是这个二元离散函数的偏导。计算图像梯度是一个一个像素点求的。
连续二元函数的偏导数为
∂f(x,y)∂x=limΔx→0f(x+Δx,y)−f(x,y)Δx∂f(x,y)∂y=limΔy→0f(x,y+Δy)−f(x,y)Δy
但是图像是离散函数,Δx 没有办法趋于 0,最小只能是间隔 1,因此使用有限差分来近似计算梯度。因此,图像偏导变成了如下形式:
∂f(x,y)∂x=f(x+1,y)−f(x,y)∂f(x,y)∂y=f(x,y+1)−f(x,y)
x,y 表示某个像素的坐标,除了上面这个前向差商外,还可以采用后向差商,中心差商来计算梯度。比如采用中心差商:
∂f(x,y)∂x=f(x+1,y)−f(x−1,y)2∂f(x,y)∂y=f(x,y+1)−f(x,y−1)2
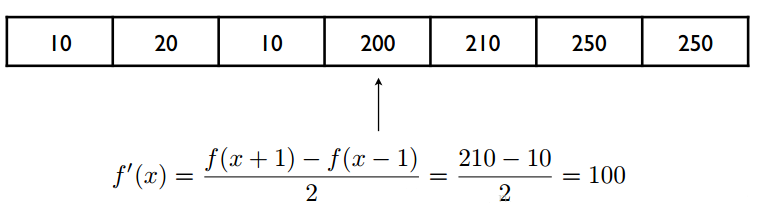
写成一维卷积的形式等于与 [−1,0,1] 这样一个滤波核作卷积。
对于离散的图像来说,一阶微分的数学表达相当于两个相邻像素的差值,根据选择的梯度算子不同,效果可能有所不同,但是基本原理不会变化。
比如 sobel 算子也可以计算梯度,本质也是通过差分计算,但是用到了前后向序列的信息,同时为每个元素附加权重。


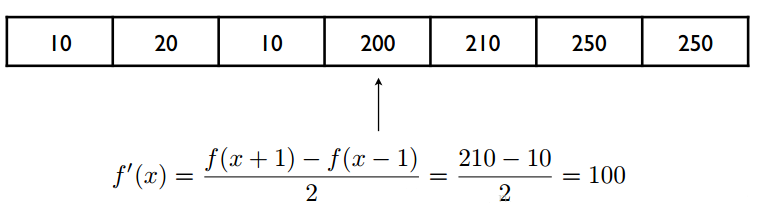






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架