Harris Corner Detection

这个博客写的不详细，有兴趣的话可以看视频：https://www.bilibili.com/video/BV1Hv411e7CW。

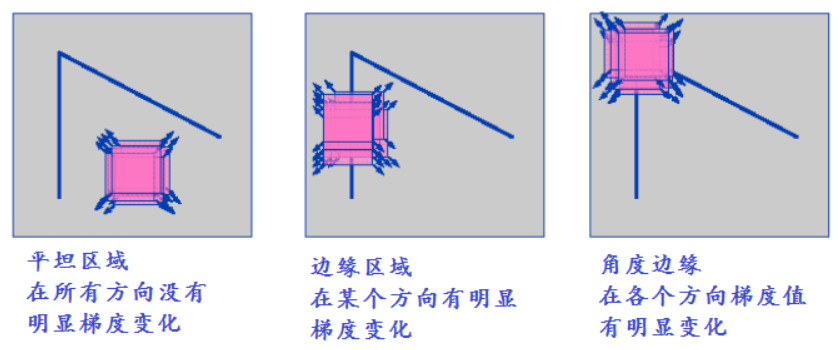
使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，窗口中的像素灰度变化程度，如果存在任意方向上的滑动，

都有着较大灰度变化，那么我们就可以认为该窗口中存在角点。举个例子，下图中 $A$ 是角点，$B$ 不是角点，如果用一个小窗口(蓝色)在点 $A$

处滑动，无论朝哪个方向走，窗口内的像素值都会发生明显的变化，比如窗口往左，那白色像素就越多，红色越少；但是对于 $B$ 点，无论朝哪

个方向滑动，窗口内的像素基本不变。

    

进一步地

      

基本数学公式如下：

$$E(u,v) = \sum_{(x,y) \in W}^{}W(x,y)\left [ I(x+u,y+v) - I(x,y) \right ]^{2}$$

其中 $w(x, y)$ 表示移动窗口，$I(x, y)$ 表示像素灰度值强度，范围为 $0-255$，$x,y$ 表示窗口内的像素坐标，$u,v$ 表示方向。

函数 $E(u,v)$ 是和图像一个窗口区域一一对应的，即首先需要用 $W(x,y)$ 确定一个窗口，然后再计算这个图像区域对应的 $E(u,v)$

函数来判断该窗口内是否存在角点。根据二元泰勒展开式：

$$I(x+u,y+u) = I(x,y) + uI_x(x,y) + vI_y(x,y) + R_n$$

去掉高阶项，原式近似为

$$E(u,v) \approx \sum_{(x,y) \in W}^{}W(x,y)\left [ uI_x(x,y) + vI_y(x,y) \right ]^{2}  = \sum_{(x,y) \in W}^{}W(x,y) \left (u^2I_x^2 + 2uvI_xIy + v^2I_y^2 \right ) \\ = \sum_{(x,y) \in W}^{}W(x,y)\begin{bmatrix} u & v  \end{bmatrix}\begin{bmatrix} I_x^2 & IxIy\\  IxIy & I_y^2 \end{bmatrix}\begin{bmatrix} u \\  v \end{bmatrix} \\  = \begin{bmatrix} u & v  \end{bmatrix}\left (\sum_{(x,y) \in W}^{}W(x,y)\begin{bmatrix} I_x^2 & IxIy\\  IxIy & I_y^2 \end{bmatrix} \right ) \begin{bmatrix} u \\  v \end{bmatrix} \\ =  \begin{bmatrix} u & v  \end{bmatrix}M \begin{bmatrix} u \\  v \end{bmatrix}$$

每个实对称矩阵累加之后还是一个实对称矩阵，所以得到的 $M$ 是一个实对称矩阵。进一步有：

$$E(u,v) \approx \begin{bmatrix} u & v  \end{bmatrix}P\begin{bmatrix} \lambda_1 & \\  & \lambda_2 \end{bmatrix}P^T \begin{bmatrix} u \\  v \end{bmatrix} \\ = \begin{bmatrix} u & v  \end{bmatrix}P\begin{bmatrix} \lambda_1 & \\  & \lambda_2 \end{bmatrix} \left (\begin{bmatrix} u & v \end{bmatrix}P \right )^T \\ = \begin{bmatrix} u^{'} & v^{'} \end{bmatrix}\begin{bmatrix} \lambda_1 & \\  & \lambda_2 \end{bmatrix} \begin{bmatrix} u^{'} \\ v^{'} \end{bmatrix} \\ = \lambda_1u^{'2} + \lambda_2v^{'2} \\ = \frac{u^{'2}}{1/\lambda_1} + \frac{v^{'2}}{1/\lambda_2}$$

可以看出函数 $E(x,y)$ 在 $xoy$ 平面的等高线就是椭圆。

我们的目标是：无论 $u,v$ 取什么值，或者说窗口 $w$ 无论沿哪个方向运动，$E(u,v)$ 都要尽可能地大。这样才符合角点的性质。

也就是说如果一个区域存在角点，那么相比与其它区域，相同的高度对应的等高线(椭圆)越小。

所以分母要尽可能地小，即特征值 $\lambda_1,\lambda_2$ 要尽可能地大。

    

当 $\lambda_1 >> \lambda_2$ 或 $\lambda_2 >> \lambda_1$ 时，检测到的就是边；当 $\lambda_1,\lambda_2$ 都很小，$E$ 接近常数，检查测到的是平坦区域；两个都很大，

并且近似一样大时，检测到的就是角点。引入一个量化的指标来衡量这种关系：

$$R = \det M - k(trace \; M) = \lambda_1\lambda_2 - \left ( \lambda_1 + \lambda_2 \right )$$

代码实现过程主要在于求得矩阵 $M$，即

$$M = \left (\sum_{(x,y) \in W}^{}w(x,y)\begin{bmatrix} I_x^2 & IxIy\\  IxIy & I_y^2 \end{bmatrix} \right )$$

假设窗口大小为 $5 \times 5$，即

$$W = \begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & w_{15} \\  w_{21} & w_{22} & w_{23} & w_{24} & w_{25} \\  w_{31} & w_{32} & w_{33} & w_{34} & w_{35} \\  w_{41} & w_{42} & w_{43} & w_{44} & w_{45} \\  w_{51} & w_{52} & w_{53} & w_{54} & w_{55} \end{bmatrix}$$

那么矩阵 $M$ 可以表示为

$$M = \begin{bmatrix} w_{11}I_x^2 & w_{11}I_xI_y \\  w_{11}I_xI_y & w_{11}I_y^2 \end{bmatrix} + \begin{bmatrix} w_{12}I_x^2 & w_{12}I_xI_y \\  w_{12}I_xI_y & w_{12}I_y^2 \end{bmatrix} + \cdots + \begin{bmatrix} w_{55}I_x^2 & w_{55}I_xI_y \\  w_{55}I_xI_y & w_{55}I_y^2 \end{bmatrix}$$

因为不好表示，所以这里每个矩阵内都写成了 $I_x,I_y$，但它们是不同的，表示图像对应窗口元素的梯度值。

就看 $M[0][0]$ 这个元素，发现其实它就是矩阵 $W$ 和矩阵 $I_x$ 在相同窗口位置的卷积值。用一个 $5 \times 5$ 的高斯核作为 $W$ 矩阵。

代码如下：

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206

#!/usr/bin/env python3 # -*- coding:utf8 -*-   import math import cv2 import numpy as np   def Conv2D(kernel, img, padding, strides=(1, 1)):     """     单通道图像卷积     """     padImg = np.pad(img, padding, "edge")     result = []     for i in range(0, padImg.shape[0] - kernel.shape[0] + 1, strides[0]):         result.append([])         for j in range(0, padImg.shape[1] - kernel.shape[1] + 1, strides[1]):             val = (kernel * padImg[i:i + kernel.shape[0], j:j + kernel.shape[1]]).sum()             result[-1].append(val)     return np.array(result)   def Map2Gray(data):     """     将数组中的元素映射到[0,255]区间     """     maxVal = np.max(data)     minVal = np.min(data)     interval = maxVal - minVal     data = np.floor(255 / interval * (data - minVal))     return data   def CalImgGrad(f):     """     用 5x5 sobel kernel 计算每个像素点的梯度     """     sobelx = np.array([         [2, 1, 0, -1, -2],         [2, 1, 0, -1, -2],         [4, 2, 0, -2, -4],         [2, 1, 0, -1, -2],         [2, 1, 0, -1, -2]     ])     sobely = np.array([         [2, 2, 4, 2, 2],         [1, 1, 2, 1, 1],         [0, 0, 0, 0, 0],         [-1, -1, -2, -1, -1],         [-2, -2, -4, -2, -2]     ])       fx = Conv2D(sobelx, f, ((2, 2), (2, 2)))     fy = Conv2D(sobely, f, ((2, 2), (2, 2)))     fx2 = fx * fx     fy2 = fy * fy     fxfy = fx * fy       return fx2, fy2, fxfy   def CalRvals(fx2, fy2, fxfy):     """     计算每个像素对应的M矩阵和R值     """     W = 1.0 / 159 * np.array([         [2, 4, 5, 4, 2],         [4, 9, 12, 9, 4],         [5, 12, 15, 12, 5],         [4, 9, 12, 9, 4],         [2, 4, 5, 4, 2]     ])     k = 0.05       fx2 = Conv2D(W, fx2, ((2, 2), (2, 2)))     fy2 = Conv2D(W, fy2, ((2, 2), (2, 2)))     fxfy = Conv2D(W, fxfy, ((2, 2), (2, 2)))       result = []     maxEValue = []   # 存储最大特征值     minEValue = []   # 存储最小特征值     for i in range(fx2.shape[0]):         result.append([])         maxEValue.append([])         minEValue.append([])         for j in range(fx2.shape[1]):             M = np.array([                 [fx2[i, j], fxfy[i, j]],                 [fxfy[i, j], fy2[i, j]]             ])             a = np.linalg.det(M)             b = np.trace(M)             """             M是实对称矩阵，按理必然存在实际特征值，可能由于精度缺失，             方程 x^2 - bx + a = 0 未必有解，所以 b ** 2 - 4 * a 取了个绝对值，             这样算出来的值就不对。             """             delta = math.sqrt(math.fabs(b ** 2 - 4 * a))             e1 = 0.5 * (b - delta)             e2 = 0.5 * (b + delta)             r = a - k * b             result[-1].append(r)             maxEValue[-1].append(max(e1, e2))             minEValue[-1].append(min(e1, e2))       g1 = Map2Gray(np.array(maxEValue))         # 最大特征值图     g2 = Map2Gray(np.array(minEValue))         # 最小特征值图     g3 = Map2Gray(np.array(result).copy())     # R图       cv2.imshow('eMax', g1)     cv2.waitKey(0)     cv2.imshow('eMin', g2)     cv2.waitKey(0)     cv2.imshow('R', g3)     cv2.waitKey(0)     cv2.destroyAllWindows()       return np.array(result), g1, g2, g3   def Sign(img, rVals):     threshold = 25 * math.fabs(rVals.mean())     judge = rVals >= threshold     rectangle = (12, 12)    # 标记矩形大小     thickness = 2           # 标记矩形边的厚度       for i in range(img.shape[0]):         for j in range(img.shape[1]):             up     = max(i - rectangle[0] // 2, 0)             bottom = min(i + rectangle[0] // 2, img.shape[0] - 1)             left   = max(j - rectangle[1] // 2, 0)             right  = min(j + rectangle[1] // 2, img.shape[0] - 1)             # 为了使矩形框不发生重叠需要进行非极值抑制             isLocalExtreme = rVals[i,j] >= rVals[up:bottom + 1, left:right + 1]             if judge[i, j] and isLocalExtreme.all():                 cv2.rectangle(img, (left, up), (right, bottom), (0, 0, 255), thickness)     return img   def HarrisCornerDetection(img):     grayImg = img.mean(axis=-1)  # 变成单通道灰度图像     fx2, fy2, fxfy = CalImgGrad(grayImg)     rVals, g1, g2, g3 = CalRvals(fx2, fy2, fxfy)     finalImg = Sign(img, rVals)     return finalImg, g1, g2, g3   # =============================================================================   def RecordVideo(fullFileName):     fps = 25     size = (640, 480)     duration = 10  # 修改录制时长，单位s     frameCount = duration * fps       cap = cv2.VideoCapture(0, cv2.CAP_DSHOW)  # 打开摄像头     videoWriter = cv2.VideoWriter(fullFileName, cv2.VideoWriter_fourcc('M', 'J', 'P', 'G'), fps, size)       print("Begin to record %ss video" % str(duration))       success, frame = cap.read()     while success and frameCount > 0:         videoWriter.write(frame)         success, frame = cap.read()         frameCount -= 1       cap.release()     print("End of recording")   def TestVideo():     fullFileName = "video.avi"     RecordVideo(fullFileName)       triggerCount = 0     capVideo = cv2.VideoCapture(fullFileName)     fps = capVideo.get(cv2.CAP_PROP_FPS)     frameInterval = int(1000 // fps)   # ms       print()     print("Begin to playback video")       ret, videoFrame = capVideo.read()     while ret:         cv2.imshow('image', videoFrame)         flag = cv2.waitKey(frameInterval)         if flag == ord(' '):             triggerCount += 1             print("[%s]st trigger detection" % str(triggerCount))             cv2.destroyAllWindows()               finalImg, g1, g2, g3 = HarrisCornerDetection(videoFrame)             cv2.imshow('image', finalImg)             cv2.waitKey(0)               cv2.imwrite("[%s]-e-max.jpg" % str(triggerCount), g1)             cv2.imwrite("[%s]-e-min.jpg" % str(triggerCount), g2)             cv2.imwrite("[%s]-R.jpg" % str(triggerCount), g3)             cv2.imwrite("[%s]-final.jpg" % str(triggerCount), finalImg)         ret, videoFrame = capVideo.read()       capVideo.release()     cv2.destroyAllWindows()     print("End of playing")   def TestImage(fullFileName):     img = cv2.imread(fullFileName)     finalImg, g1, g2, g3 = HarrisCornerDetection(img)     cv2.imshow('image', finalImg)     cv2.waitKey(0)     cv2.destroyAllWindows()   TestVideo() # TestImage("2.jpg")